Abstract
The vibration signals of a gearbox always contain the dynamic operation information, which are important for the feature extraction and further work. However, the low signal-to-noise ratio and combined multi-mode faults make it difficult to extract discriminable features of gearboxes. In this study, a feature fusion method based on wavelet packet decomposition (WPD), singular value decomposition (SVD) and t-Distributed stochastic neighbor embedding (t-SNE) for gearbox fault diagnosis is proposed. First, time-frequency analysis method of WPT-SVD as well as time-domain analysis methods are utilized to extract robust feature vectors of gearboxes with different conditions. As an effective method for the visualization of high-dimensional datasets, t-SNE is then introduced to realize the dimensionality reduction of feature vectors. Finally, with the fused features, a radial basis function (RBF) neural network is trained to realize the classification of gearbox fault modes. Sufficient experiments have been implemented to validate the effectiveness and superiority of the proposed method by analyzing the vibration signals of gearboxes.
1. Introduction
As one of the most important machine components, gearboxes are extensively used in transmission design of many rotating machine. However, the severe operation conditions of heavy duty and intensive impact load may result in gear tooth damage and other fault modes, which heavily influences the working condition of the whole systems [1]. In order to reduce the operation and maintenance costs for gearboxes, numerous studies have been conducted to realize the gearbox fault recognition [2, 3]. But the low signal-to-noise ratio and combined multi-mode faults make it still a challenge to extract discriminable features for gearboxes. This study provides a feature fusion method based on wavelet packet decomposition (WPD), singular value decomposition (SVD) and t-Distributed stochastic neighbor embedding (t-SNE) for gearbox fault diagnosis.
For fault diagnosis, one of challenges is to obtain reliable features of the gearbox by analyzing the monitoring vibration signals in the first step. Generally, the main feature extraction methods include time-domain methods, frequency-domain methods, and time-frequency methods. Time-domain analysis methods such as root-mean-square (RMS) value, crest factor, form factor, kurtosis and skewness have been successfully used to realize fault diagnosis of rotating machine [4]. Frequency-domain analysis methods include Fourier transform, cepstrum analysis and so on. As for time-frequency analysis methods such as short-time Fourier transform (STFT) and empirical mode decomposition (EMD), they have been proven effective to extract features from nonlinear and non-stationary vibration signals [5]. Among these time-frequency techniques, WPD is one of the best tools since it has particular advantages for decomposing original signals into different frequency bands. And the SVD method can be utilized to form the final feature vectors based on the results of WPD. To extract robust representatives for the gearbox, both time-domain analysis methods and time-frequency analysis method of WPT-SVD are applied in this study.
Mapping the extracted high-dimensional feature representatives into low-dimensional space properly is another challenge in this paper. A large number of dimensionality reduction techniques have been proposed, such as PCA, KPCA and manifold learning methods like local tangent space alignment (LTSA) [6]. However, most of these methods have the limitation to capture both the local and global structure of the high-dimensional features. To realize the presence of clusters at several scales, Maaten et al. proposed the t-SNE method which can achieve good visualization of high-dimensional data [7]. In this study, t-SNE is employed as the dimensionality reduction method to get the most discriminable features.
Inspired by the aforementioned challenges, a novel feature fusion method for gearbox fault diagnosis is proposed in this study. Our contributions are summarized as follows: Firstly, we proposed an effective feature extraction method relying on WPD-SVD and time-domain analysis methods for gearboxes. The extracted robust feature vectors embody the key information of gearbox operation condition. Secondly, a t-SNE based dimensionality reduction method is employed to obtain the discriminable features, relying on which fault diagnosis can be realized with a RBF neural network model. Moreover, sufficient experiments are conducted by comparing with the existing methods based on the operation data of gearboxes, which demonstrates the feasibility and effectiveness of our proposed approach.
The rest of this paper is organized as follows. In Section 2, we explain the overall scheme of fault diagnosis and the mathematical principles. The results of case study are provided and analyzed in Section 3, followed by our conclusion in Section 4.
2. Methodology
2.1. Procedures of the method
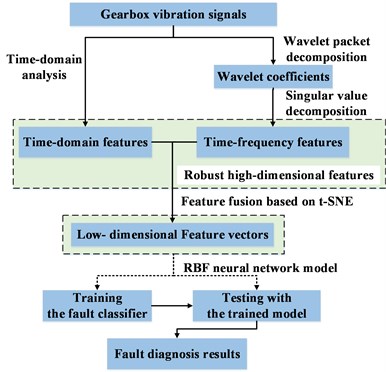
The procedure of our methodology is shown in Fig. 1. This paper provides a fault diagnosis methodology which contains two main steps as below:
– In the first step, time-domain analysis methods, including the RMS value, crest factor, form factor, kurtosis and skewness, are applied to extract the time-domain features of gearboxes, while the WPD-SVD method is employed to form the time-frequency feature vectors.
– The second step involves dimensionality reduction of the extracted feature vectors based on t-SNE. Relying on the obtained low-dimensional fused features, the RBF neural network model can be trained to realize the fault mode classification.
2.2. Feature extraction based on time-domain analysis and WPD-SVD
2.2.1. Time-domain analysis
The time-domain parameters of the original signals including the mean value, the maximum value, the RMS value, etc. In this study, the RMS value, crest factor, form factor, kurtosis and skewness are chosen to form the time-domain features of gearboxes.
If xs(t) denotes a set of sampling data x1,x2,...,xN, the five chosen time-domain parameters are calculated as follows:
– The RMS value: α=xrms=√1N∑Ni=1(xi)2.
– The crest factor: β=max(x)/xrms.
– The form factor: γ=1Nxrms/∑Ni=1|xi|.
– The kurtosis: σ=1N∑Ni=1(xi-mean(x)/var(x))4.
– The skewness: ε=1N∑Ni=1(xi-mean(x)/var(x))3.
Then the time-domain feature vectors of gearboxes can be expressed as C=[α,β,γ,σ,ε].
Fig. 1The procedure of the proposed methodology
2.2.2. Wavelet packet decomposition and singular value decomposition
The method of WPD has the framework of multi-resolution analysis based on wavelet analysis. The function of wavelet packet Wnj,k(t) can be expressed as:
where n denotes the decomposition level, j denotes the scale factor, and k denotes the translation factor.
Here the original signal in time domain is defined as f(t), and the sampling rate is fs. If the signal f(t) is decomposed by WPD with level J, 2J group of wavelet packet coefficients can be obtained. The ith wavelet packet coefficients can be expressed as:
Then, the SVD method can be used to extract the prominent features from the wavelet packet coefficients. The singular values of wavelet packet coefficients can be utilized to represent time-frequency features in this study.
2.3. Feature fusion based on t-SNE
2.3.1. SNE method
SNE is introduced based on the spirit of converting the high-dimensional Euclidean distances between data points into conditional probabilities that represent similarities. The similarity of data point xj to data point xi is the conditional probability, which can be denoted as pj|i:
where σi indicates the variance of the Gaussian distribution that is centered on data point xi, and pi|i is set as zero.
For the low-dimensional mapping values yi and yj corresponding to the original xi and xj, the similarity qj|i between them can be calculated by:
where δ=1/√2 and qi|i is set as zero.
In order to make pi|i match qj|i best, the sum of Kullback-Leibler divergences over all data points is minimized by a gradient descent method. The cost function is expressed as:
where Pi represents the distribution of pj|i, and Qi represents the distribution of qj|i.
2.3.2. t-SNE method
As an extension of Stochastic Neighbor Embedding (SNE), t-SNE was proposed for visualizing high-dimensional data [7]. To optimize the cost function more effectively, t-SNE was proposed with two improvements. Firstly, a symmetric version of SNE cost function is selected by minimizing a single Kullback-Leibler divergence between the joint probability distribution P in the high-dimensional space and Q in the low-dimensional space, respectively:
where pij and qij are expressed as:
To solve the problem that the widely separated data tend to be crowded in the low-dimensional space, t-SNE employs a Student-t distribution rather than a Gaussian distribution to convert distances into probabilities in the low-dimensional space. Then qij can be defined as:
And the gradient is modified as:
By solving the problems of SNE cost function, t-SNE can realize better dimensionality reduction of high-dimensional datasets.
3. Case study
The dataset in the 2009 PHM Conference Data Analysis Competition is applied in this paper.
The gearbox dataset consists of two types of gearboxes and fourteen kinds of fault modes. Data were collected at 30, 35, 40, 45 and 50 Hz shaft speed while being subjected to either high or low loading. To demonstrate the feasibility and effectiveness of the proposed method, we choose six typical conditions of spur gearboxes including one normal state and five fault states under 40 Hz as listed in Table 1.
Table 1Description of fault modes in the experiment
Case | Normal | Fault 1 | Fault 2 | Fault 3 | Fault 4 | Fault 5 | |
Gear | 32T | Good | Chipped | Good | Good | Chipped | Good |
48T | Good | Eccentric | Eccentric | Eccentric | Eccentric | Good | |
80T | Good | Good | Good | Broken | Broken | Broken | |
Bearing | IS:IS | Good | Good | Good | Ball | Inner | Inner |
ID:IS | Good | Good | Good | Good | Ball | Ball | |
OS:IS | Good | Good | Good | Good | Outer | Outer | |
Shaft | Input | Good | Good | Good | Good | Good | Imbalance |
3.1. Feature extraction of the gearbox vibration signals
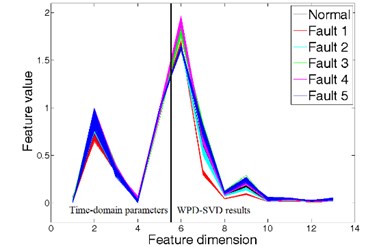
For each state of gearboxes, 200 samples are generated with every 5000 data points. In the process of feature extraction, each sample is firstly used to obtain five time-domain parameters: the RMS value, crest factor, form factor, kurtosis and skewness. These time-domain feature vectors are normalized to eliminate the dimension effects. Then the sample is decomposed to acquire eight wavelet packet coefficients by WPD with the decomposition level 3. Based on the wavelet packet coefficients, the singular values which can represent the time-frequency features of gearboxes are obtained by SVD. The time-domain parameters and the WPD-SVD results together constitute the robust feature vectors of gearboxes, as shown in Fig. 2.
Fig. 2The results of feature extraction
3.2. Feature fusion based gearbox fault diagnosis
In this section, t-SNE is utilized to fuse the high-dimensional feature vectors of gearboxes. The former 13-dimensional features are reduced to be 3-dimensional features, which can be seen as the key representatives of gearboxes. To evaluate the effectiveness and superiority of t-SNE method, the traditional methods of PCA and LTSA are also applied to the same dataset. The perplexity of t-SNE method is set as 25. By comparing the results of the different methods, we can find that the results of t-SNE have the best visualization effects as well as the best separability in low-dimensional feature space, as shown in Fig. 3.
Based on the low-dimensional fused features given by t-SNE, further fault diagnosis can be carried out. Here, 150 samples from normal condition and five fault modes are selected to train the RBF model, respectively. With the trained classification model, 50 samples from each state are chosen for testing as the model input. The samples of the PCA results and the samples of the LTSA results are also implemented to verify the classification performance.
As showed in Table 2, the accuracy rate of fault diagnosis based on t-SNE can reach 100 %, while other feature fusion methods cannot cluster all the fault states of gearboxes clearly, which results in low accuracy of classification. The result of fault mode classification verifies the effectiveness and superiority of the proposed feature extraction and feature fusion method.
Fig. 3The results of feature fusion
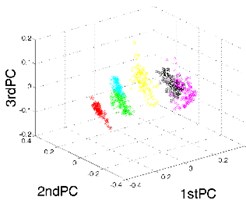
a) Result of PCA
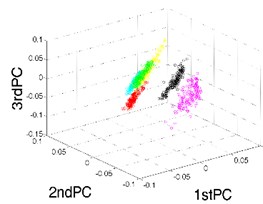
b) Result of LTSA
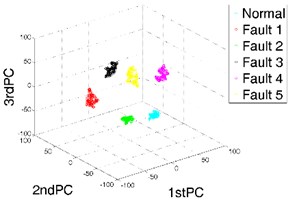
c) Result of t-SNE
Table 2Accuracy of classification using different methods
Method | Total | Normal | Fault 1 | Fault 2 | Fault 3 | Fault 4 | Fault 5 |
t-SNE | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
PCA | 0.9600 | 1 | 1 | 0.8200 | 1 | 0.9600 | 0.9800 |
LTSA | 0.8567 | 0.9600 | 1 | 0.8000 | 1 | 0.9600 | 0.4200 |
4. Conclusions
In this paper, a novel method of feature fusion based on WPD-SVD and t-SNE for gearbox fault diagnosis is proposed. In the first step, several time-domain parameters and singular values based on WPD-SVD are both obtained by processing the vibration signals of gearboxes, which together constitute the robust feature vectors. Then, t-SNE, as an effective method for the visualization of high-dimensional datasets, is introduced to realize dimensionality reduction of the extracted feature vectors. Based on the fused features, a RBF based fault diagnosis model is applied to achieve the gearbox fault mode classification. Sufficient experiments have been implemented to demonstrate the effectiveness and superiority of the proposed method by analyzing the vibration signals of gearboxes.
References
-
Chaari F., Fakhfakh T., Haddar M. Dynamic analysis of a planetary gear failure caused by tooth pitting and cracking. Journal of Failure Analysis and Prevention, Vol. 6, Issue 2, 2006, p. 73-78.
-
Lin J., Zuo M. J. Gearbox fault diagnosis using adaptive wavelet filter. Mechanical Systems and Signal Processing, Vol. 17, Issue 6, 2003, p. 1259-1269.
-
Wang J., Jiang C., Han Z., et al. Network association strategies for an energy harvesting aided super-wifi network relying on measured solar activity. IEEE Journal on Selected Areas in Communications, Vol. 12, 2016, p. 3785-3797.
-
Sreejith B., Verma A. K., Srividya A. Fault diagnosis of rolling element bearing using time-domain features and neural networks. 3rd international Conference on Industrial and Information Systems, 2008, p. 1-6.
-
Liu B., Riemenschneider S., Xu Y. Gearbox fault diagnosis using empirical mode decomposition and Hilbert spectrum. Mechanical Systems and Signal Processing, Vol. 20, Issue 3, 2006, p. 718-734.
-
Zhang Z., Zha H. Principal manifolds and nonlinear dimensionality reduction via tangent space alignment. Society for Industrial and Applied Mathematics, 2005.
-
Hinton G. E. Visualizing high-dimensional data using t-SNE. Vigiliae Christianae, Vol. 9, Issue 2, 2008, p. 2579-2605.
About this article
This study is supported by the Fundamental Research Funds for the Central Universities (Grant No. YWF-17-BJ-J-42 and YWF-16-BJ-J-18) and the National Natural Science Foundation of China (Grant Nos. 51605014 and 51575021), as well as the Technology Foundation Program of National Defense (Grant No. Z132013B002).

