Seismic performance of box-plate, box-plate with UNP, box-plate with L-plate and ordinary rigid beam-to-column moment connections

1. Introduction

Before the North Ridge Earthquake in 1994, structures that had lateral resisting systems with rigid frames were considered as the most ductile and most earthquake resisting compared with other similar systems, but the earthquake resulted in lots of damage in steel rigid structures that had welded beam-to-column connections. Numerous studies were done and they showed that the reason for all the damage was different brittle fractures in the welded connections; such fractures prevent the connections’ inelastic behavior and hence reduce the structure ductility. Thereafter, many researches were carried out to improve the behavior of the welded moment connections; the summary of some of which (more recent ones) are provided in this paper, and based on them some novel connections, studied in the FEM software, have been proposed [1].

Chen et al. studied the longitudinal toothed connection and its bending capacity through laboratory tests and simulation methods. The study showed that it prevented brittle fractures (in the beam penetration part), and reduced stress concentration at the connection end which hence prevented the flange failure. Using the FEM Software and the ANSYS Software, the study showed that local stress concentration was reduced, plastic hinge was formed at a good distance from the column, the system showed appropriate ductility (without any brittle fractures), and according to the diagrams, the tested models reached 3 % of the required plastic bending moment while the connection remained in its elastic state [2].

Tehranizadeh et al. studied the effects of the upper and lower plates on the bending rigidity of the restrained joints using three, real-size beam-to-column connections all tested under hysteretic loading. The results, validated through simulations in the ABAQUS Software, revealed that the deformations were nearly similar in all three models. Other findings worth noting in their study are: 1) some kind of fracture or rupture was observed in the flange-web connection line around the plastic hinge, 2) an increase in the plate length caused an improvement in the required plastic bending moment which increased the local buckling of the web and flange around the plastic hinge, 3) an expansion in the local buckling caused an increase in the failure potential of the plastic hinge, 4) in the web plate connection, since the plastic hinge was formed at the end of the upper plate, no damage occurred to the upper plate-to-web slot weld, and 5) in models with longer flange connection plates, the slot weld rupture in the web-to-flange line occurred around the plastic hinge; the reason being the plate length which increased the plastic strain in that area. Accordingly, they suggested that it would be beneficial if the flange plates had the shortest lengths, welding materials would be high-strength (resistant), so the upper and lower plates’ thicknesses for welding were the highest allowable [3].

Wang et al. studied the effects of the longitudinal plate connection in the center of a beam web on the beam-to-column connection, investigated the ductility increase of the connection of a column to a beam with uncompressed flange by welding a longitudinal strengthening plate to its web, and showed, through real-size model tests, that such plates were quite effective in delaying the local buckling in the web. The connection had considerable effects on enhancing the beam-to-column ductility and the results of the tests performed in this research were validated using the FEM numerical studies and the ABAQUS Software [4].

Mohammad Ali Kafi et al. studied a new idea of a rigid connection to the minor axis of built-up I-shaped columns by haunch plates. Initially, data from rigid beam to column flange connection were used to verify numerical analysis and results, owing to the unavailability of experimental data concerning rigid beam to web connection. Thereafter, seven numerical models of one-sided subassembly of beam to column web connection with different arrangements of the haunch plates, and vertical and horizontal continuity plates were designed and assessed by means of finite element method using ABAQUS. After that, parameters such as restraint percentage, stiffness, strength, plastic hinge location, and ductility under cyclic loads were calculated for each model. His effort was indicated that adding haunch plates along with horizontal and vertical continuity plates in the panel zone of double I-shaped columns could lead to significant increases in connection stiffness, as it restricts a relative rotation of the tip of top and bottom connection plates [5].

A steel structure is an assembly of load bearing members, which are linked through numerous connections for the purpose of forming an integrated and stable system, able to carry all subjected loads. It should then be noted that the behavior of connections plays an important role in how the structure responds. Lack of knowledge about the behavior of connections, and their inaccurate design, may increase the extent of damages induced to the structure in case of an earthquake. The rigid connection’s specifications such as restraint percentage, stiffness, strength, and ductility have also been studied before. Nevertheless, no published paper was found on a rigid connection to the web side of the columns. Thus, considering the fact that this connection is not a prequalified one, a thorough study must in addition to providing construction details, evaluate the cyclic behavior of this connection in a subassembly model, and satisfy code measures such as stiffness, restraint percentage, strength, and ductility, especially according to Iran’s code regulations, AISC2005, and FEMA350 as well. In the present research, one novel rigid connection is introduced and compared, for their ductility and moment capacity, with typical restrained connections through their related moment-rotation diagrams drawn under similar regular dimensions, loading, and boundary conditions; when rotation is more than 4 %, the connection is a special bending frame connection. To do this research, use was made of the restrained connection utilized in the models. To make sure of the manual model dimensions, use was made of the AISC for the sections and sizes of the welding and connection plates with no loading combination coefficients; these sections were then modeled in the finite element software [3, 4, 6-8].

2. Methodology

In this research, the typical and novel connections have been studied by the FEM under ultimate and hysteretic loading, and their performances have been compared through their moment-rotation diagrams. This research uses weld and beam-to-column sections, and interacts them together with ties and friction interaction to do modeling in the ABAQUS by virtue of the papers validated by laboratory methods and the mentioned software. As the weld and connections are more important and require higher precision, use was made of finer meshes for their modeling. The models underwent reciprocal loading, and their moment-rotation diagrams were drawn for better comparisons. In the finite element analyses, use was made of the linear failure model the details of which will be explained in the next section along with the research methodology [8-11].

For a better study of the finite element model and the modeling verification, first, the beam to column connection investigated by Tehranizadeh et al was modeled in the ABAQUS, and then its finite element analyses’ results were compared with those of the laboratory tests. In short, the dimensions of the beam-column plates, connections, and welds (Table 1), their materials specifications (Table 2), and the materials behavior (Fig. 1) were used in the ABAQUS finite element software as inputs. As shown in Table 2, the mechanical specifications of the materials used in the software for the beam-column plates and welds are different; (the interactions of all the welded plates used in the software were of a contact type). It is obvious that in the box-plate connection, the web plate on its side is connected to the column plate, and its two sides are connected to the beam flange plate by 6 mm weld. (For better analyses, appropriate mesh sizes were selected for modeling, but the meshes were smaller for welds and connection plates because of their higher importance). The mesh size was 20 mm for welds, 30 mm for connection plates, and 40 mm for beams and columns. The simulation models of the ordinary typical and box-plate connections are shown in Figs. 2 and 3 respectively [9].

At the end of this research, the equations are proposed by Matlab Software that they can calculated ultimate moment and plastic moment for all of the connections that they are introduced in this study. It is used from the regression method for finding these equations by Matlab software. In this investigation, it is proposed 2 type equations (linear and non-linear). The variables of the linear equations are thickness and length of the connection plates and the variable of the non-linear equation is inertia moment of the connections [12].

Fig. 1Stress-strain relationship in the ABAQUS software [9]

Fig. 2Simulation of an ordinary typical connection and boundary conditions in the ABAQUS software [9]

Fig. 3Simulation of the box-plate, box-plate with UNP and box-plate with L-plate connection in the ABAQUS Software [9]

a) Simulation of the Box-Plate connection model [9]

b) Simulation of the Box-Plate with UNP connection [9]

c) Simulation of the Box-plate with L plate connection [9]

2.1. Analytical model

2.1.1. Interstory drift angle

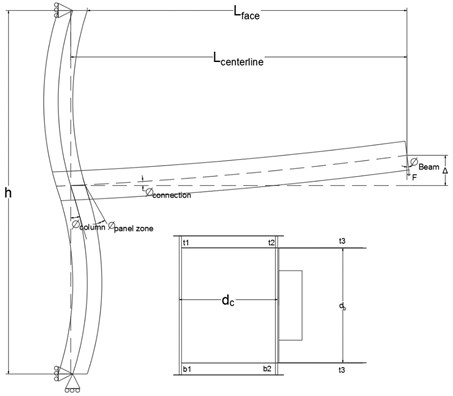
Interstory drift angle is a combination of both elastic and inelastic rotations assumed to be almost the same as joint rotation of the model. On the contrary, elastic rotation of joint is negligible and major rotation of the sub-assembly model is dedicated to column and beam rotations. In AISC314(2005) as well as FEMA351(2000), cyclic load pattern, classifying connections to special, intermediate, and ordinary moment frames, and calculating rotation capacities are all based on interstory drift angle. Fig. 4 depicts terms used in formulas calculating required rotations and moments. Eqs. (1) and (2) show how to calculate interstory drift angle and moment at column face, respectively. Panel zone rotation and connection components rotation can yield by Eqs. (3) and (4), and adding up these two equations result in Eq. (5) which is joint rotation or total connection rotation [7, 8]:

1

${\theta }_{InterstoryDrift}=\frac{∆}{L_{CenterLine}},$

2

$M_{CenterLine}=F\times L_{CenterLine},$

3

${\mathrm{\varnothing }}_{PanelZone}=\frac{X_{b1}+X_{b2}-X_{t1}-X_{t2}}{2d_b}+\frac{y_{b1}+y_{b2}-y_{t1}-y_{t2}}{2d_c},$

4

${\mathrm{\varnothing }}_{Connection}=\frac{\left(X_{b3}-X_{b2}\right)-(X_{t3}-X_{t2})}{d_b},$

5

${\mathrm{\varnothing }}_{Joint}={\mathrm{\varnothing }}_{PanelZone}+{\mathrm{\varnothing }}_{Connection}.$

Fig. 4How to calculate required moments and rotation of connection assembly

2.1.2. Panel zone rotation

Panel zone deforms under shear forces due to moments induced to the column by beams. These deformations because of shear strains can rotate panel zone. Therefore, panel zone rotation is shear strain in the joint. Fig. 5 shows how to calculate this rotation:

6

$\gamma =\frac{\sqrt{a^2+b^2}}{2ab}\left({\delta }_1-{\delta }_2\right).$

where $a$ and $b$ are panel zone dimensions, and ${\delta }_1$ and ${\delta }_2$ are changes in rectangle’s diameters.

2.1.3. Connection components rotation

Connection components rotation is the most significant term in determining whether a connection is rigid, semi-rigid, or simple. Nonetheless, connection classification is based on total connection rotation, which is a combination components rotation and panel zone rotation.

2.1.4. Total connection rotation

Total connection rotation is needed to determine if a connection is rigid, semi-rigid, or simple. AISC 360(2005) suggests that total connection rotation is defined as summation of panel zone, connection of components, and initial length of beam rotation. Total connection rotation is schematically illustrated in Fig. 6 where $\gamma$ is panel zone rotation, ${\mathrm{\varnothing }}_c$ shows connection components rotation, and ${\mathrm{\varnothing }}_j$ is the total connection rotation.

Fig. 5Panel zone rotation calculation by Mazzolani [13]

a)

b)

Fig. 6Joint rotation by Mazzolani [13]

a)

b)

c)

3. Verification with laboratory test

For a better study of the finite element model and the modeling verification, first, the beam-to-column connection investigated by Tehranizadeh et al was modeled in the ABAQUS, and then its finite element analyses’ results were compared with those of the laboratory tests. Fig. 7 shows comparing FEM model with the laboratory test that carry out with Tehranizadeh et al. [3, 11, 9].

4. Findings

Fig. 8 shows the moment-rotation curve of a typical connection and Fig. 9 shows three different typical curves of moment-rotation for fully restrained (FR), partially restrained (PR), and simple (S) connections. Fig. 10 shows protocol load in this research, Fig. 11 shows the bending capacity, and Fig. 16 shows energy dissipation of the ordinary and four box-plate connections under the application of 34 similar loading cycles (of the displacement type), and Fig. 11 shows their moment-rotation diagrams.

As shown, an increase in the connection hardness increases its bending capacity; in other words, box-plate connections can tolerate more cycles of the reciprocal loading. In addition, the connections with no brittle failure have rotated more than 4 radians. The ordinary connection reaches a moment value of 456.625 KN.M at cycle 34th while box-plate connections reach this value at cycles 27th and 28th respectively; therefore, energy dissipation is more in the box-plate than any other connection. Fig. 11 shows that box-plate with UNP connection is more restrained than the ordinary connection. Fig. 12 shows the moment-rotation curves of the models in the first cycle. With the instructions shown in Figs. 11 and 12, it is possible to calculate the bending capacity and stiffness of the connections. It is clear that the tangent of the graph shows stiffness for models [7-9, 11, 13].

Fig. 7Comparing the ordinary model in ABAQUS with Laboratory result of Tehranizadeh investigation [3, 9, 11]

4.1. Connection stiffness

AISC 2005 categorizes connections in terms of three important behavioral parameters, which are stiffness, strength, and ductility. These behavioral parameters are derived from moment-rotation curve of connection sub-assembly. Fig. 11 illustrates a typical moment-rotation curve [7].

Fig. 8Moment-rotation curve of a typical connection [7, 8]

Fig. 9Three different typical curves of Moment-rotation for fully restrained (FR), partially restrained (PR) and simple (S) connections [7, 8]

The expressions used in above curve are explained as follows:

Regarding moment-rotation curve of a connection two stiffness parameters are defined for each connection. Initial stiffness of connection $K_i$ (which is not a practical term), and secant stiffness is $K_s$ (defined as $K_s=M_s/{\theta }_s$ where $M_s$ and ${\theta }_s$ are respectively moment and rotation of the connection under service loads). The connection is considered fully restrained (FR) when $K_s$ is larger than 20EI/L, i.e. relative rotation of beam and column can be ignored. Nominally simple (S) when $K_s$ is less than 2EI/L, i.e. the joint rotates without any resistance, and partially restrained (PR) when the stiffness is between these two limits, that is, their stiffness, strength, and ductility should be taken into account in analysis and design of the structure. EI and L are flexural rigidity and length of the beam, respectively. These three types of connections are depicted in Fig. 9.

4.4. Loading history

The specimens were subjected to the loading sequence proposed by AISC seismic provisions for testing of beam-to-column moment connection. Cyclic loading history is shown in Fig. 10 [7].

Fig. 10Displacement-time analyses of all the models [9]

5. Simulation results

5.2. Connection moment-rotation hysteretic curves

To determine stiffness of a connection pursuant to AISC 314(2005), moment-rotation hysteretic curves for the analyzed connections are drawn in Fig. 11 [7].

Fig. 11Moment-rotation curves of models under 34 loading cycles [9]

a) Moment-rotation curves of ordinary model

b) Moment-rotation curves of Box plate connection (thickness = 8 mm)

c) Moment-rotation curves of Box plate connection (thickness = 10 mm)

d) Moment-rotation curves of Box plate connection (thickness = 15 mm)

e) Moment-rotation curves of Box plate connection (thickness = 20 mm)

f) Moment-rotation curves of Box plate connection (thickness = 15 mm) and UNP6

g) Moment-rotation curves of Box plate connection (thickness = 8 mm) and UNP8

h) Moment-rotation curves of Box plate connection (thickness = 10 mm) and UNP8

i) Moment-rotation curves of Box plate connection (thickness = 15 mm) and UNP8

j) Moment-rotation curves of. Box plate connection (thickness = 10 mm) and L-plate connection (thickness = 10 mm)

k) Moment-rotation curves of Box plate connection (thickness = 10 mm) and L-plate connection (thickness = 12 mm)

5.3. Stress and strain contours

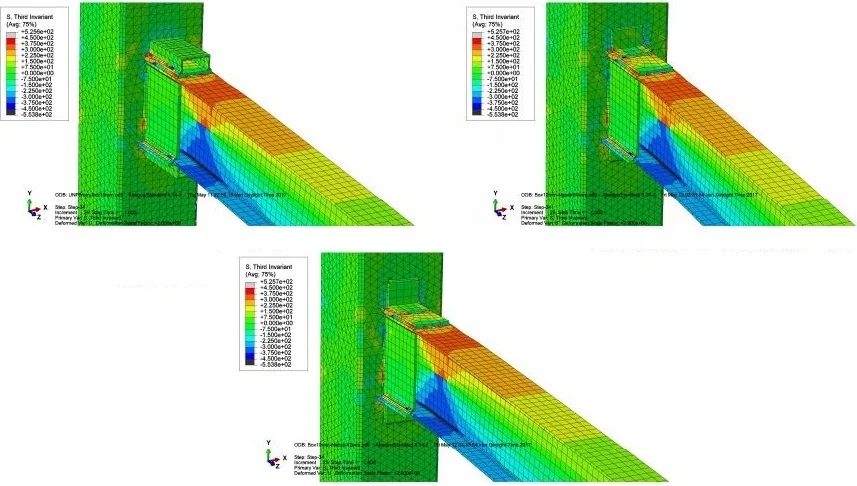
Von-Third Invariant and equivalent plastic strain contours for numerical models of beam to column web rigid connection using Box-plate with UNP, Box-plates, Box-plate with L-plates at $\theta =$ 0.05 rad are illustrated in Fig. 12 and Fig. 13 respectively. Maximum values were set to 450 MPa for stress, and 0.1361 for strain. What can be derived from these contours is that the stiffer the models get, the farther plastic hinges are moved from the connection.

Fig. 12 shows the stress at the end of the 34th loading cycle in the models respectively, and shows that stress has been concentrated at the point where the column and upper plate connect. Also, Fig. 12 shows that in the box-plate and box-plate with UNP connection, stress concentration is lower than the other models in the upper and lower plates [9].

Fig. 13 shows the plastic strain in the 34th loading cycle in the ordinary and box-plate connections respectively. In the ordinary, UNP and L plate models; the plastic strain at the junction of the upper and lower plates is 2.55 and 2.43 times those in the 11 models shown. Fig. 13 shows the plastic hinge was created next to the panel zone. The plastic hinge has the greatest area the in box-plate and box-plate with UNP models, but it has little area in the ordinary model [9].

Fig. 12Triaxial stress in eleven models [9]

a) Ordinary model

b) Box plate connection thickness = 8 mm

c) Box plate connection thickness = 10 mm

d) Box plate connection thickness = 15 mm

e) Box plate connection thickness = 20 mm

f) Box plate connection

g) UNP8 and Box plate connection thickness = 8 mm

h) UNP8 and Box plate connection thickness = 10 mm

i) UNP8 and Box plate connection thickness = 15 mm

j) Box plate connection thickness = 10 mm and L-plate connection thickness = 10 mm

k) Box plate connection thickness = 10 mm and L-plate connection thickness = 12 mm

Fig. 13Plastic strain in eleven models [9]

a) Ordinary model

b) Box plate connection thickness = 8 mm

c) Box plate connection thickness = 10 mm

d) Box plate connection thickness = 15 mm

e) Box plate connection thickness = 20 mm

f) Box plate connection thickness = 15 mm and UNP6

g) UNP8 and Box plate connection thickness = 8 mm

h) UNP8 and Box plate connection thickness = 10 mm

i) UNP8 and Box plate connection thickness = 15 mm

j) Box plate connection thickness = 10 mm and L-plate connection thickness = 10 mm

k) Box plate connection thickness = 10 mm and L-plate connection thickness = 12 mm

Fig. 13 shows pushover curves of eleven models under 34 loading cycles. The integral of this graph is cumulative energy dissipation. It is clear that the tangent of the pushover curve shows stiffness in the model, so comparing the curves in Fig. 14 you can find the best connection. Fig. 15 shows the limits of stiffness for the simple connection and rigid connection. Energy dissipations for the models is calculated as integral of the graph in Fig. 14. The results of this calculation is shown in Fig. 16 [7-9].

Fig. 14Pushover curves of eleven models under 34 loading cycles [9]

a) Ordinary model

b) Box plate connection thickness = 8 mm

c) Box plate connection thickness = 10 mm

d) Box plate connection thickness = 15 mm

e) Box plate connection thickness = 20 mm

f) Box plate connection thickness = 15 mm and UNP6

g) UNP8 and Box plate connection thickness = 8 mm

h) UNP8 and Box plate connection thickness = 10 mm

i) UNP8 and Box plate connection thickness = 15 mm

j) Box plate connection thickness = 10 mm and L-plate connection thickness = 10 mm

k) Box plate connection thickness = 10 mm and L-plate connection thickness = 12 mm

6. Discussion and comparison on numerical models

6.2. Study on the connection’s stiffness as stated in AISC 314(2005)

In order to classify connections based on their stiffness, as AISC 314(2005) suggests, the moment-rotation push curves of the connections were drawn. In view of these curves, secant stiffness ($K_s$) is defined as $M_s$/${\theta }_s$, in which $M_s$ is the moment of beam under service loads, and is measured by $M_s=f_y*S$ where $f_y$ indicates steel yield stress. $S$ is elastic section modulus, and ${\theta }_s$ shows beam rotation under service loads. As it is tabulated in Table, and what has been mentioned in introduction about stiffness measures, all the models are qualified to be used as fully restrained connections (with $K_s$ greater than 20). Our concerted effort was to restrict the connection components rotation instead of the panel zone rotation. The test results showed that the major part of rotations in beam to column connections with plates and UNP is dedicated to connection components rotation, and not to panel zone rotation [7].

Table 3Percent restraint values for beam to column web connections

Model name	Percent restraint
a	89 %
b	86 %
c	86 %
d	86 %
e	86 %
f	85 %
g	85 %
h	85 %
i	85 %
j	85 %
k	85 %

Table 4Stiffness calculation for the numerical models of beam to column web connection

Model name	$M_s$ (KN.M)	$\theta s$	$K_s$ (KN.M)	$I_x$ (cm4)	$K_{s}L$ / EI
a	264.63	0.008788	30112.65	12880.85	2.92
b	264.63	0.00689	38407.83	12880.85	3.72
c	264.63	0.006877	38480.44	12880.85	3.73
d	264.63	0.006892	38396.69	12880.85	3.73
e	264.63	0.006887	38424.56	12880.85	3.72
f	264.63	0.006848	38643.39	12880.85	3.75
g	264.63	0.006845	38660.33	12880.85	3.75
h	264.63	0.006838	38699.91	12880.85	3.75
i	264.63	0.006828	38756.59	12880.85	3.76
j	264.63	0.006848	38643.39	12880.85	3.75
k	264.63	0.006851	38626.47	12880.85	3.74

Fig. 15Two different typical curves of moment-rotation for fully restrained (FR), partially restrained (PR), and simple (S) connections [7, 8]

6.5. Study on the equations of the moment capacity

In this section, it is introduced the 4 equations for calculation of ultimate moment and plastic moment these connections. For finding the equations that they can calculate ultimate moment capacity and plastic moment capacity, it is used from regression method by MATLAB software. Eq. (7) and Eq. (8) show respectively two non-linear equations for calculation ultimate moment capacity and plastic moment capacity.

Eq. (9) and Eq. (10) show respectively two linear equations for calculation ultimate moment capacity and plastic moment capacity that the variable of these equations is moment inertia. Table 7 shows plastic and ultimate moment capacity that they are calculated by MATLAB and ABAQUS software. Table 8 shows maximum, minimum, mean errors and the standard deviation for each 4 equations. Fig. 16 shows curves that they are showed comparing the results MATLAB and ABAQUS software [12]:

7

$M_e=0.75941\times b_u+1.08343\times t_u+0.69936\times b_d+0.93041\times t_d+0.99487\times X+0.02487\times d_w+0.06313\times t_w+0.05687\times U+0.01917\times h_{unp}+0.00274\times b_{unp}+0.00147\times t_{unp}+0.16415\times L+0.00865\times h_L+0.25524\times t_L,$

8

$M_p=0.59459\times b_u+1.00214\times t_u+1.21313\times b_d+0.95311\times t_d+0.99479\times X+0.010559\times d_w+0.085919\times t_w+0.00022\times U+0.00227\times h_{unp}+0.00205\times b_{unp}+7.32E5\times t_{unp}+24421\times L+1.33E-5\times h_L+0.020978\times t_L,$

9

$M_e=-6.28514E-50\times I^6+2.36932E-40\times I^5-3.642E-31\times I^4+2.92053E-22\times I^3-1.28869E-13\times I^2+2.96913E-05\times I-2419.305935,$

10

$M_p=2.21143E-51\times I^6-3.91873E-42\times I^5-1.52384E-33\times I^4+8.03214E-24\times I^3-6.94869E-15\times I^2+2.48918E-06\times I+135.9771436.$

where $M_e=$ ultimate moment capacity of connection (kN.m), $M_p=$ plastic moment capacity of connection (kN.m), $I=$ inertia moment (mm⁴), $b_u=$ the wide of the upper plate connection (mm), $t_u=$ the thickness of the upper plate connection (mm), $b_d=$ the wide of the down plate connection (mm), $t_d=$ the thickness of the down plate connection (mm), $X=$ number of the box plate connection, $d_w=$ the length of the box plate connection (mm), $t_w=$ the thickness of the box plate connection (mm), $U=$ number of the UNP connection, $b_{unp}=$ the wide of UNP plate, $t_{unp}=$ the thickness of UNP plate, $h_{unp}=$ the high of UNP plate, $L=$ number of the $L$ plate, $h_L=$ the wide of $L$ plate, $t_L=$ the thickness of $L$ plate.

Table 8 shows the Max, min, mean errors and the standard deviation for each equation that they are introduced. Correlation coefficients are more than 0.99 for each equation [12].

Table 7Plastic moment and ultimate moment are calculated by MATLAB and ABAQUS software [12]

Model	$M_e$ (ABAQUS simulation)	$M_e$ (MATLAB simulation)	$M_e$ (MATLAB simulation)	$M_p$ (ABAQUS simulation)	$M_p$ (MATLAB simulation)	$M_p$ (MATLAB simulation)
	–	Eq. (7) linear	Eq. (9) non-linear	–	Eq. (7) linear	Eq. (9) non-linear
A (1st model)	362.3475	362.348	362.366	456.625	456.620	456.610
B (2nd model)	373.975	374.293	374.229	462.760	463.309	463.009
C (3th model)	375.0975	374.419	374.757	464.058	463.481	463.759
D (4th model)	374.5925	374.735	374.823	464.435	463.910	464.478
E (5th model)	374.8325	375.051	375.196	464.268	464.340	464.304
F (6th model)	376.62	376.911	376.602	464.013	464.241	464.068
G (7 model)	376.7675	377.486	377.092	463.930	463.794	463.967
H (8th model)	377.19	377.612	377.395	464.058	463.966	464.018
I (9 model)	377.8475	377.928	378.131	464.350	464.395	464.369
J (10 model)	376.435	378.165	375.996	463.998	464.179	464.042
K (11th model)	376.7725	378.848	377.221	463.968	464.221	463.877

Table 8The maximum, minimum, mean, variance and standard deviation for each equation [12]

°	Eq. (7)	Eq. (8)	Eq. (9)	Eq. (10)
Max error	0.00119131	0.000642742	0.005509345	0.001242637
Min error	4.79683E-05	3.29993E-05	2.76807E-12	1.19735E-05
Mean errors	0.000707178	0.000182074	0.001612251	0.000522333
Variance	1.34718E-07	3.92223E-08	2.98902E-06	1.89053E-07
Standard deviation	0.00036704	0.000198046	0.001728878	0.000434802

Fig. 17(a) shows the result of the linear equations, that they calculated by MATLAB and ABAQUS software. Fig. 17(b) shows the result of the 6 degrees polynomial equation that only the variable of these equations is inertia moment [12].

Fig. 17(a) shows comparing the results that they are calculated linear functions by MATLAB software and ABAQUS software. Fig. 17(b) shows comparing the results that they are calculated by MATLAB software with ABAQUS software. Fig. 17(b) shows comparing the results of the non-linear equations that are calculated by MATLAB software with ABAQUS software [12].

Fig. 16Cumulative energy dissipation of five models under 34 loading cycles [9]

a) The curve of the cumulative Energy dissipation of five models under 34 loading cycles [9]

b) Enlarging the curve of the cumulative Energy dissipation of five models under 34 loading cycles [9]

Fig. 17a) Comparing the results that they are calculated with linear equations by ABAQUS and MATLAB softwares, b) comparing the results that they are calculated from non-linear equations with the ABAQUS results [12]

a)

b)

7. Conclusions

The modeling of the ordinary, box-plate, box-plate with UNP, box-plate with L-plate, L-plate, and UNP connections under hysteretic loading showed that:

• They all rotated more than 4 radians in the 34th loading cycle meaning that according to the AISC Seismic Code they can be used in the Special Moment Frame systems.

• The bending moment capacity of the box-plate with the UNP model is 6.2 % more than that of the ordinary model. This connection had maximum bending capacity in this research.

• The area under the moment-rotation curve revealed that energy dissipation in the box-plate (15 mm) with UNP (Num8) model is 4.3 % more than that in the ordinary model.

• In the box-plate UNP model, the stress concentration in the upper and lower plates is more than those of the ordinary model, and its value at the web center is 1.06 times that of the upper and lower plates.

• Tangent curve of moment-rotation shows all of the models are semi-rigid connection, and they are in partially restrained zone. Fig. 14 shows stiffness of box-plate with UNP connection is more than the other models. This model can damp energy more than the ordinary model.

• There is not much difference for the seismic performance among these models.