Crack breathing behavior of unbalanced rotor system: A Quasi-static numerical analysis

1. Introduction

The breathing of fatigue cracks is a primary cause of machine failure. The failure of a machine can be catastrophic, and produce economic issues as well as personal injury. A fatigue crack commonly presents itself on a rotating shaft due to the loads, torsional efforts, and lateral vibration occurs as a result of rotational mass unbalance. Since shafts are a fundamental component of high speed rotating machinery used in aerospace, nuclear, oil, transportation and industry processes in general, the issue of fatigue crack generation and propagation in a shaft becomes more significant [1, 2]. The presence of a crack in a mechanical component can alter shaft vibration behavior in ways including the increase of displacement and the decrease in frequency due to a rise in component flexibility [3, 4].

The early detection of the vibration signs of a cracked rotor is often based on vibration analysis where many different methods have been proposed to detect the shaft crack and predict vibration responses of a cracked rotor [5, 6]. The success of these methods largely depended on the accuracy of the crack breathing model that describes the crack opening and closing during shaft rotation. Early switch model assumed that a crack changes its states from fully open to fully closed when the crack rotates to a horizontal position [7, 8]. The issue relating to this model is that the chaotic and quasi-periodic vibrations due to the sudden change of the crack state have not been seen in the experimental tests [9, 10]. Later, the modification was made to the switch model to give a smooth and gradual change of the crack opening and closing status by using different trigonometric functions [11, 12]. For this transient breathing model, the crack status remains fully open and fully closed at two singles positions, where the crack points downwards and upwards, respectively. However, it was demonstrated that the crack actually remains fully open or fully closed for a range of shaft rotation angles [13]. A new crack breathing mechanism was proposed by Al-Shudeifat et al. [14] where the crack was no longer seen to be fully open or fully closed at a single rotation angle.

The actual crack breathing behavior can be predicted by using three-dimensional finite elements methods. Bachschmid et al. [15] investigated breathing of a straight front crack and a helicoidally crack in term of the shaft deflection during a complete rotation. A simply cracked cylindrical beam was used in this numerical simulation where one end of the beam was clamped and the other end was loaded mechanically. A two-dimensional finite element analysis using ABAQUS was performed by Fay [16] where the breathing of a crack was investigated in terms of mixed mode I/II stress intensity factor of a crack. The Mode I stress intensity factor for an elliptical breathing crack was determined in [17]. Liong and Proppe [18] analyzed crack breathing, using a cohesive zone model of a three-dimensional finite element, and the shaft stiffness loss during rotation of the shaft. In their work, both ends of the shaft were supported rigidly. The breathing of a straight front crack represented by the local flexibilities was studied in a three-dimensional finite element shaft model with a fixed end boundary condition applied to the shafts support ends [19, 20].

The studies mentioned above assumed that the only force affecting the crack breathing is rotor weight, which is likely to be true for the heavy rotors. A few studies have been recommended where the weight-only breathing models may not be suitable for lightweight rotors, vertical rotors or rotors operating around their critical speed of rotation [21, 22], as there is significant influence from dynamic loads. Rubio et al. [13, 17] highlighted the influence of the eccentricity on the breathing behavior in a rotating cracked shaft in terms of crack opening percentage and stress intensity factor. It was found that addition of an unbalance force has a large influence on the crack breathing mechanism.

Mobarak et al studied the effect of crack location on the crack breathing behavior in an analytical paper [23], where the opening percentage of a crack was calculated quantitatively. In this work, we will present our results from finite element analysis. The breathing mechanism of a transverse crack in a two-disc rotor is investigated numerically under the coupling influence of unbalance force and rotor weight using a three-dimensional finite element model. Both ends of the shaft are fixed, which represents a more realistic boundary condition than simply supported ends. Under the fixed end support boundary condition and unbalance force effect, a crack will breathe differently at different locations along the shaft length. Crack breathing is represented by the crack closing percentage. The simulations were performed using the commercial finite element code, ABAQUS/Standard. The results obtained from the unbalanced shaft model are also compared with the balanced shaft, where only rotor weight is considered. It should be mentioned that Rubio’s [13] work employed a classical Jeffcott rotor simply supported at both ends, with a massless shaft and a disc at the mid-span of the shaft. In this rotor and unbalance force configuration, crack breathing will remain the same regardless of the crack location. Therefore, only the crack breathing behavior at the shaft mid-span was examined by the authors. Further, the effect of unbalance force magnitude on the breathing was not evaluated.

2. Modeling of the unbalanced rotor system

The simulation is conducted as a series of static problems with different crack locations along the shaft length in axial and angular positions. A transverse straight crack with non-dimensional crack depth ratio, $\mu =h/R$, has been simulated where $h$ is the crack depth in the radial direction and $R$ is the shaft radius. $A_{crack}$ is the area of the crack segment as shown in Fig. 1(a). The unbalance force has been taken as a rotational force and its angular position $\beta$ with respect to the crack direction on the shaft cross-section plane is shown in Fig. 1(b).

Fig. 1Schematic diagrams of a) crack cross-section and b) relative orientation between unbalance force and the crack on the shaft cross-section plane

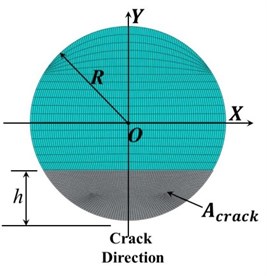
a)

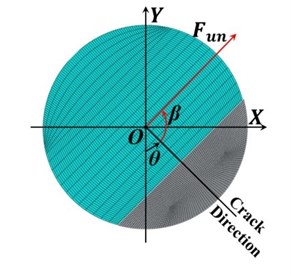
b)

Fig. 2Simulation details for the crack cross-section and mesh around the crack in a) transversal and b) longitudinal direction

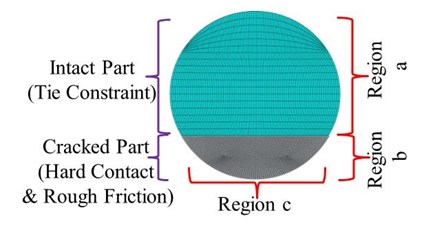
a)

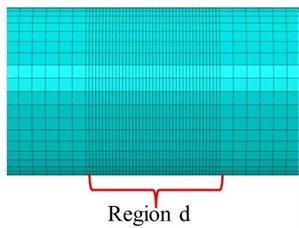
b)

The two shaft is joined together to generate a crack section using ‘Tie Constraints’ function that establishes the intact part of the cracked section. The contact interaction is defined in finite element numerical model as a normal and the tangential properties of the created cracked surfaces. To prevent the penetration between the crack surfaces when the crack closes, the normal property ‘hard contact’ is selected. To avoid the sliding between the crack surfaces the tangential property ‘rough friction’ is applied to generate an infinite friction coefficient. The simulation details for the crack cross section are displayed in Fig. 2(a) where the upper part is the intact section while the lower area corresponds to the cracked section of the shaft. The shaft is meshed by using an element named C3D8R. The mesh size is obtained after a convergence test of the results through mesh sensitivity analyses. As shown in Fig. 2, the mesh density is much higher around the crack in the transversal direction and longitudinal direction. The results of the convergence test for balanced case, with a crack at the midpoint of the shaft and a shaft rotation angle 90°, are presented in Table 1. It is seen that the closing percentage converges after the numbers of mesh in four regions, denoted as a, b, c and d in Fig. 2, reach 18, 36, 80 and 40. The percentage of closing will be described later in detail.

Fig. 3Schematic diagram of the unbalanced two-disk rotor system model

A full three-dimensional finite element model for a two-disk rotor is simulated with fixed end supports since the rotor symmetry no longer exists in the unbalanced shaft as shown in Fig. 3. The total shaft length, $L$, is 724 mm and the radius, $R$, is 6.35 mm. The shaft is made of steel with the following mechanical properties: Young’s Modulus, $E=$210 GPa, Poisson ratio, $\nu =$0.3 and density, $\rho =$7800 kg/m³.

The shaft is rotated anticlockwise and the crack has an original direction along the negative $Y$-axis. The following configurations of crack location and unbalance force are considered:

a) 40 different axial crack locations, $\lambda$, along the shaft length varying from 0 to 1 with an increment of 0.025.

b) 24 different angular positions of the cracks, $\theta$, varying from 0° to 360° with an increment of 15°.

c) 5 different unbalance force ratios, $\eta =$ 5, 10, 20, 100 and ∞ (balanced), the ratio of the rotor weight (shaft + two disks) to the unbalance force, $F_{un}$.

d) 5 different angular position of unbalance forces, $\beta =$ 0°, 45°, 90°, 135° and 180°. Only half angular range of unbalanced force (0° to 180°) has been considered because of the symmetry.

e) 4 different crack depth ratios, $\mu =$ 0.25, 0.5, 0.75 and 1.

The shaft self-weight, $m_{s}g$, has been applied as a gravitational force and two disk weights, $2m_{d}g$, have been applied as the concentrated force at 181 mm from the two shaft ends. $m_s$ is the mass of the shaft and $m_d$ is the mass of a disk ($m_d=$0.5 kg). The unbalanced force, $F_{un}$, has been also applied as a concentrated force in $X$-axis $\left[m_{s}g+2m_{d}g/\eta \right]\times \mathrm{s}\mathrm{i}\mathrm{n}(\theta +\beta )$ and in $Y$-axis $\left[m_{s}g+2m_{d}g/\eta \right]\times \mathrm{c}\mathrm{o}\mathrm{s}(\theta +\beta )$ at the right disk.

3. Results and discussion

The crack breathing behavior is analyzed by the calculated percentage of the closed area of a crack, $Ʌ$, as described in Eq. (1). Where $A_{crack}$ is the area of the crack segment as shown in Fig. 1(a) and $A_{closed}$ is the closed portion of the crack area during the rotation as shown in Fig. 4. $A_{crack}$ has been calculated by Eq. (2) where $\mu$ is the non-dimensional crack depth and $R$ is the shaft radius. $A_{closed}$ has been obtained directly from ABAQUS history outputs by selecting History Output Request/Contact/CAREA (Total area in contact). In ABAQUS, a crack area is treated as being closed when the area is under the compression and $A_{closed}$ is calculated accordingly. For a fully open and fully closed crack, the percentage of a crack closed area, $Ʌ$, is equal to 0 % and 100 % respectively:

To verify the ‘Tie constraint’ crack, the specific fracture tool ‘Seam’ in ABAQUS is also chosen to create a crack. The seam tool duplicates the nodes at the cracked section to allow a crack to open and close during the shaft rotation. The percentages of the closing of the crack using Tie constraint has been compared with those obtained using the seam tool. Fig. 5 shows an excellent agreement between two methods for a crack at the middle span of the balanced shaft. In this work, Tie constraint crack has been used.

Fig. 4The representation of closed portion of the crack segment

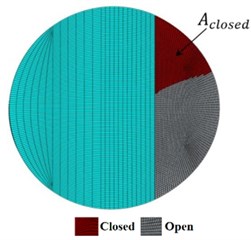
Fig. 5Comparison between the “Tie Constraint” crack and “Seam” crack at the middle span of the balanced shaft

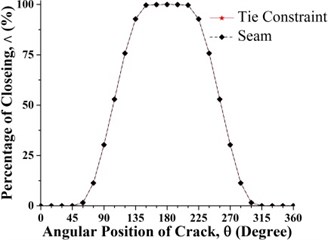
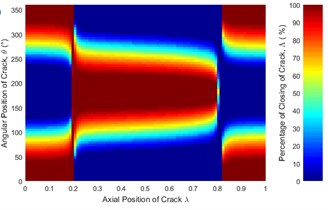
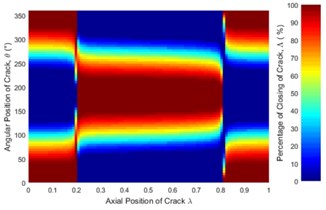
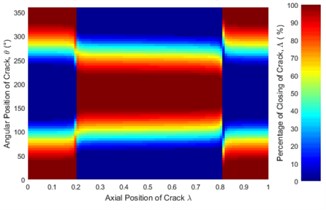
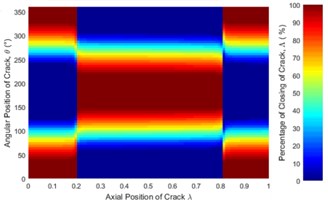
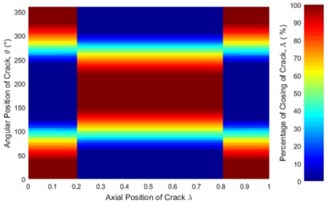
Fig. 6Statues of the crack along the shaft length for different force ratios: a) η= 5, b) η= 10, c) η= 20, d) η= 50, e) η= 100 where β= 0° and f) η=∞ (balanced)

a)

b)

c)

d)

e)

f)

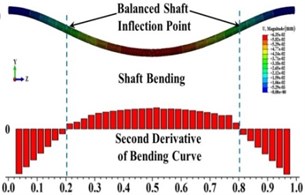
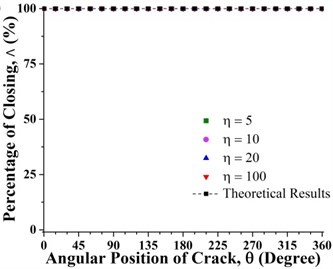
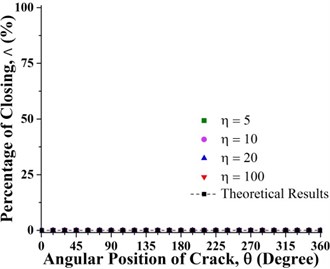
The statuses of a crack at different axial and angular position along the shaft length for different force ratios including balanced case are shown in Fig. 6. Crack statuses strongly depend on the crack axial position and unbalanced force ratio. However, as force ratio increases (unbalance force decreases), the crack statuses progressively approach to the balanced shaft. The crack statuses are symmetrical about the angular position of crack $\theta =$180° but about the axial position of crack, it is no longer symmetrical. Two special axial crack locations are identified at around 0.2 and 0.8, where the status of crack remains the same for all unbalanced force ratios (see Fig. 8). But, crack statuses are different for each crack locations. At around 0.2, it is fully closed and the crack never opens during rotation. The shaft stiffness would be maximum like an uncracked shaft. On the other hand, at around 0.8, the crack is fully open and never closes during rotation. The shaft stiffness would be minimum. This is because rotor weight does not introduce any shaft bending at these two locations. It can be easily understood from Fig. 7(a), where the slope of the shaft bending curve at either 0.2 or 0.8 is zero and shaft bending direction changes by 180 degrees across either one of two inflection points. Since the balanced shaft percentage of the closing of crack remains constant but has sharp jumps at crack locations 0.2 and 0.8 (see Fig. 6(f)). At this two-point, in the unbalanced shaft the crack opening and closing are determined by the unbalance force only. At former location, the shaft bends upwards, keeping the crack closed while at the latter it bends downwards, keeping the crack open. It can be easily understood from Fig. 7(b). Fig. 8 also demonstrates the reliability of simulation results as they are in good agreement with analytical results which are calculated using method in [23].

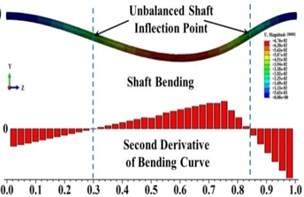
Fig. 7Shaft bending and the second derivative of bending curve for a) balanced shaft and b) due to unbalanced force only (β= 0°, θ= 0°)

a)

b)

Fig. 8Percentage of the closing of crack over a full shaft rotation for different force ratios at crack axial locations a) 0.2 and b) 0.8 where β= 0°

a)

b)

At others crack axial location, the crack statuses undergo transition when the angular position of the crack changes. When the crack is located between 0 to 0.2 and 0.8 to 1, it experiences a sequential transition from fully closed, partially open/closed, fully open, partially open/closed and then changes to fully closed status. When the crack is located in the middle region between 0.2 and 0.8, the crack status changes from fully open, partially open/closed, fully closed, partially open/closed to fully open. This is also clearly visualized in Fig. 9.

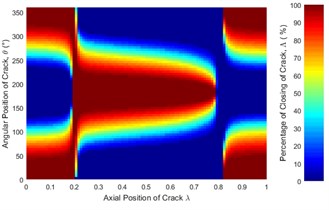
Fig. 10 illustrates the crack breathing as a function of crack axial location. The stiffness variation of the unbalance shaft can be divided into three regions bordered at $\lambda =$0.2 and 0.3. If the crack is located at two side regions, the cracked unbalance shaft will experience a stiffening process corresponding to the increase in the percentage of the closing of crack and a softening process If the crack is located at middle region.

Fig. 9Effect of unbalance force on crack breathing behavior at a) 0.15 and b) 0.7 where β= 0°

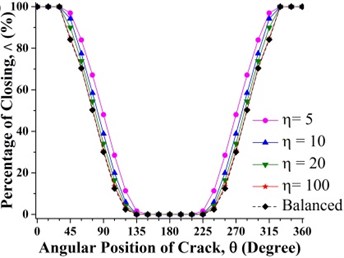
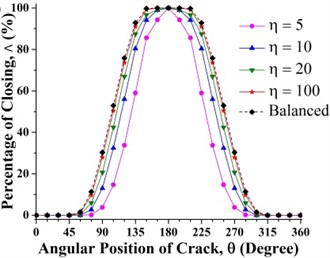
Fig. 10Percentage of the closing of a crack along the shaft length for different force ratios where β= 0°

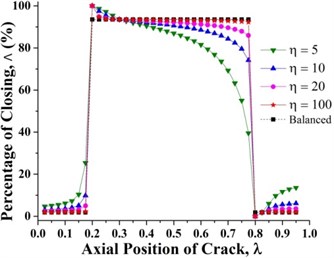
Fig. 11 clearly shows that unbalance force has no effect on the crack breathing and the crack breaths exactly like in the balanced shaft during shaft rotation at 0.3 and 0.825. The reason for this is that unbalance force does not contribute to shaft bending at 0.3 and 0.825 as shown in Fig. 7(b). The crack breathing is controlled solely by the rotor weight (Refer to Fig. 7(a)). Again, simulation results are verified by the analytical calculations as shown in Fig. 11. But, sequences of the crack statuses are different for each crack locations, the crack starts with a fully open status at 0.3 while it begins with a fully closed status at 0.825, which can be observed in Figs. 6 and 11. As a result, if a crack is located around these two locations, the stiffness of the unbalanced shaft would be the same as the balanced shaft.

Fig. 11Percentage of the closing of crack over a full shaft rotation for different force ratios at crack axial locations a) 0.3 and b) 0.825 where β= 0°

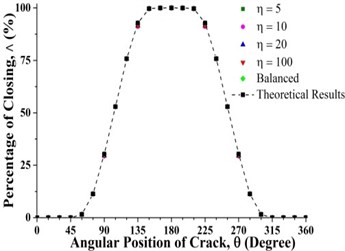
a)

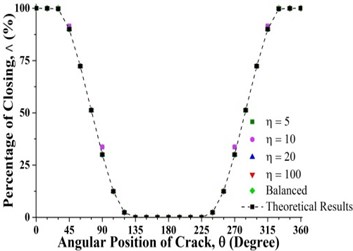
b)

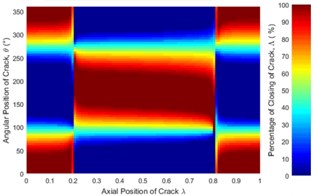
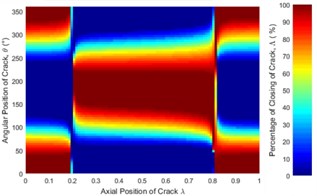
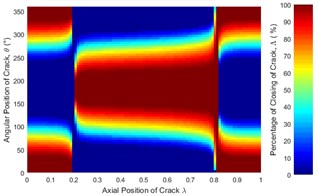
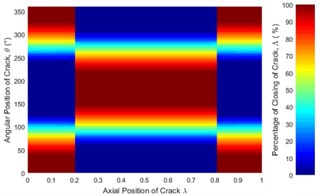
Fig. 6 represent only a case where the unbalance force aligns with the crack direction ($\beta =$0°). The effect of angular position of unbalance force on the crack statuses at a different axial position along the shaft length can be observed in Fig. 12. It is clearly seen that the crack status highly depends on the angular position of unbalance force. The crack statuses are symmetrical about $\theta =$180° only for the angular positions of unbalance force at $\beta =$0° and $\beta =$180°. This can also be clearly visualized in Fig. 13.

Fig. 12Statues of the crack along the shaft length for different angular position of unbalance force with the crack direction: a) β= 0°, b) β= 45°, c) β= 90°, d) β= 135°, e) β= 180° where η= 10 and f) η=∞ (balanced)

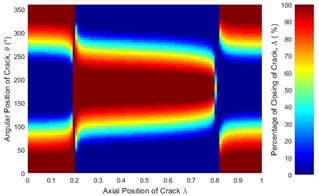
a)

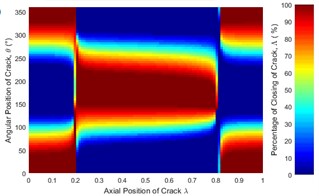
b)

c)

d)

e)

f)

As shown in Fig. 13(b) where the crack is located between 0.3 and 0.825, the percentage of the closing of crack at any $\theta$ is lower than that of the balanced shaft for $\beta =$0° and $\beta =$45°. Therefore, the unbalance shaft is more flexible. When the $\beta =$135° and $\beta =$180° the unbalanced shaft is stiffer than the balanced shaft. The stiffest unbalanced shaft is seen at $\beta =$180°.On the other hand, the results at crack locations between 0 and 0.3, and 0.825 and 1 are opposite to those in the middle span (Fig. 13(a)). Further, the percentage of the closing of crack for $\beta =$90° can be larger or smaller than that of a balanced shaft, depending on the angular position of the crack. This phenomenon is Thus, the stiffness of an unbalanced cracked shaft for a full rotation would have a little different from a balanced cracked shaft. However, as discussed previously in Fig. 7(b), crack breathing is independent of the angular position of unbalance force at boundary locations 0.3 and 0.825, where the status of crack is solely determined by the rotor weight.

Effect of crack depth ratio on crack breathing behavior is shown in Figs. 14 and 15. It is clear that crack statuses of unbalanced shaft strongly depend on crack depth ratio. As crack depth ratio increases the percentage of closing decreases. This can be visualized clearly by the constantly decreasing of the maroon colored areas (100 % closing percentage) with the increasing of crack depth ratio. At boundary location 0.2, the crack remains fully closed while at 0.8 the crack remains fully open. These boundary breathing behaviors are not affected by the crack depth ratio.

Fig. 13Effect of unbalance force orientation on crack breathing behavior at a) 0.15 and b) 0.7 where η= 10

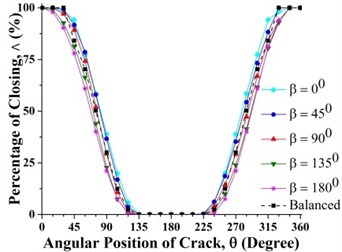
a)

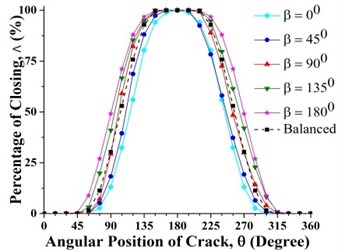
b)

Fig. 14Statues of the crack of unbalanced shaft along the shaft length for different crack depth ratios: a) μ= 0.25, b) μ= 0.5, c) μ= 0.75 and d) μ= 1 where η= 10 and β= 0°

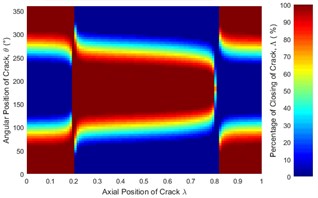
a)

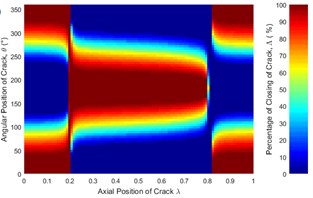
b)

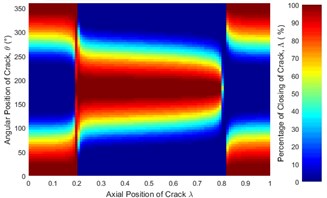
c)

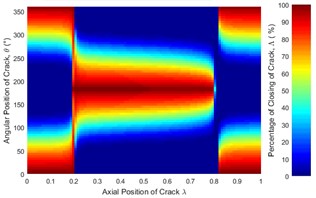
d)

Fig. 15Effect of crack depth ratios on crack breathing behaviour at a) 0.15 and b) 0.7 where η= 10 and β= 0°

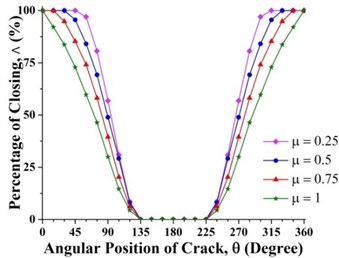
a)

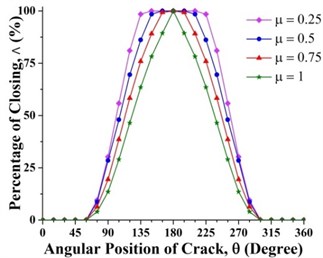
b)

4. Conclusions

In this paper, a large number of finite element simulations have been performed to examine the effects of crack axial position, crack angular position, crack depth ratio, unbalanced force ratio and angular position of unbalanced force on the crack breathing. It is found that the crack breathing strongly depends on the different combinations of these factors. In particular, the dependence of crack breathing on the crack location along shaft length is discussed in detail. Four specific crack locations along the shaft length have been identified, where the crack shows unique breathing behaviors. Further, the stiffness of the cracked shaft can change significantly from one crack location to the others.

The results obtained in this work have a significant impact on the numerical calculation and prediction of dynamic response of cracked rotors as well as the development of online crack detection techniques based on vibration signals. For example, as it is known that the crack remains fully closed and the cracked shaft will behave like an intact shaft at $\lambda =$0.2, this would generate difficulty in detecting a crack at this location, based on vibration response. In a recently published paper [24], the authors demonstrated that in a Jeffcott rotor under some unbalance force orientations and magnitudes, the typical peak at one-third of resonance frequency due to a crack could disappear as the crack became fully closed during shaft rotation. At $\lambda =$0.8, a crack will never close during shaft rotation and a breathing crack would become a notch. To predict the response of a rotor with a crack at this location, the result would be inaccurate if a breathing crack model is used. The existence of these special locations is not limited to the rotor used in this study. This kind of special locations should also exist in other common rotors. With the simplified crack breathing model of weight dominance (balance shaft), crack breathing is independent of crack location. This study shows that more accurate prediction for the dynamic response and damage severity detection of cracked rotors should consider the effect of crack location on the crack breathing.