Dynamic problem in 3D thermoelastic half-space with rotation in context of G-N type II and type III

Santra, S.; Lahiri, A.; Das, N. C.

doi:10.21595/mme.2017.18143

Mathematical Models in Engineering

Browse Journal

Submit article

Published: 30 June 2017

Check for updates

Dynamic problem in 3D thermoelastic half-space with rotation in context of G-N type II and type III

S. Santra¹

A. Lahiri²

N. C. Das³

¹Gargi Memorial Institute of Technology, Kolkata, 700144, India

^{2, 3}Department of Mathematics, Jadavpur University, Kolkata, 700032, India

Corresponding Author:

S. Santra

Cite the article Download PDF

Downloads 1337

CrossRef Citations 2

Abstract

In this paper, comparison between G-N model of type II (without energy dissipation) and G-N model of type III (with energy dissipation) has been shown in a three dimensional thermoelastic half space with rotation subjected to time dependent heat source on the traction free boundary. Eigenvalue methodology has been adopted to solve the equations resulting from the application of the Normal mode analysis to the non-dimensional coupled equations. Variation of the numerically computed values of thermal stresses and temperature with and without rotation has been illustrated graphically.

1. Introduction

The inconsistency of heat conduction equation of classical uncoupled theory of thermoelasticity with the experimental results is due to the fact that i. no elastic term is included to account for elastic changes producing heat effects; ii. parabolic nature of heat conduction equation indicating infinite speed of propagation of heat waves means that thermal disturbances (with infinite speed) and elastic disturbances (with finite speed) from the classical theory of thermoelasticity, are coupled together. This suggests that every solution of the equations has a part which extends to infinity.

Biot [1] developed a theory of irreversible thermodynamics and gave a satisfactory derivation of the linear theory of coupled thermoelasticity. In order to obtain a wave type heat conduction equation the concept of generalized thermoelasticity was introduced modifying CCTE and later extended by Dhaliwal and Sherief [3] for anisotropic body, and the uniqueness of the solutions was proved by Ignaczak [2, 4]. Green-Naghdi proposed a generalized thermoelasticity by modifying the energy equation. There are three types of constitutive relations in G-N model [6-8]. Type-I leads to classical heat conduction equation. Type-II provides solutions for thermal waves propagating finite speed without energy dissipation (TEWOED) and type-III also confirms propagation of thermal waves of finite speed with energy dissipation (TEWED). Several investigations with these extensions have been studied by Abd-Alla and Abo-Dahab [11], Kar and Kanoria [9] and Yousef [10]. Pal et al. [5, 14] studied the effect of homogeneity of the surface waves in anisotropic media.

In this paper, the stress distributions and temperature variation has been depicted in an anisotropic triclinic half space for G-N model II and III both with rotation.

2. Basic equations

For a linear thermoelastic anisotropic body subjected to rotation the field equations are as follows:

The equation of motion in the absence of inner heat source:

1

τ_{i j, i} = ρ [{\ddot{u}}_{i} + \bar{Ω} \times (\bar{Ω} \times {\bar{u}}_{i}) + (2 \bar{Ω} \times {\dot{\bar{u}}}_{i})] .

Heat – conduction equation in absence of body force:

2

k^{*} θ_{, i j} + k_{i j} {\dot{θ}}_{, i j} = ρ c_{e} \ddot{θ} + θ_{0} β_{i j} {\ddot{u}}_{i, j} .

The Duhamel-Neumann stress-strain relations are:

3

τ_{i j} = c_{i j k l} e_{k l} - β_{i j} θ δ_{i j},

where $β_{i j} = c_{i j k l} α_{k l} (i, j, k, l = 1, 2, 3) .$

Strain – displacement relation:

4

e_{i j} = \frac{1}{2} (u_{i, j} + u_{j, i}), u_{i, j} = \frac{\partial u_{i}}{\partial x_{j}},

where the differentiation with respect to space variable $x_{i}$ is denoted by and that with respect to time is denoted by notation.

3. Formulation of the problem

Let us consider a linear anisotropic thermoelastic half space within $\{(x_{1}, x_{2}, x_{3}) : 0 \leq x_{1} < \infty, 0 \leq x_{2} < \infty, 0 \leq x_{3} < \infty\}$ for a time dependent heat source on the boundary plane to the surface $x_{1} =$ 0. The surface $x_{1} = 0$ is assumed to be traction free and the body is assumed initially at rest. The components of displacement vectors of three dimensional plane waves in anisotropic elastic medium, are given as:

5

u_{i} = u_{i} (x_{1}, x_{2}, x_{3}, t), i = 1, 2, 3,

where $t$ is the time variable and $x_{i}$ , $(i = 1, 2, 3)$ denotes the respective orthogonal Cartesian co-ordinate axes. The elastic medium is now considered as rotating uniformly with an angular velocity $Ω = Ω \hat{n}$ , where $\hat{n}$ is the unit vector along the direction of rotation. The equation of motion of the rotating frame contains two additional terms: ( $Ω$ ×( $Ω$ × $u$ ) representing the centripetal acceleration due to time varying motion only and (2 $Ω$ × $\dot{u}$ ) representing the coriolis acceleration and $\hat{n} =$ (1, 0, 0).

Using Hook’s law, the stress- strain- temperature relations can be written as follows:

6a

τ_{11} = c_{11} e_{11} + c_{12} e_{22} + c_{13} e_{33} + 2 (c_{14} e_{23} + c_{15} e_{13} + c_{16} e_{12}) - β_{11} θ,

6b

τ_{22} = c_{21} e_{11} + c_{22} e_{22} + c_{23} e_{33} + 2 (c_{24} e_{23} + c_{25} e_{13} + c_{26} e_{12}) - β_{22} θ,

6c

τ_{33} = c_{31} e_{11} + c_{32} e_{22} + c_{33} e_{33} + 2 (c_{34} e_{23} + c_{35} e_{13} + c_{36} e_{12}) - β_{33} θ,

6d

τ_{23} = c_{41} e_{11} + c_{42} e_{22} + c_{43} e_{33} + 2 (c_{44} e_{23} + c_{45} e_{13} + c_{46} e_{12}),

6e

τ_{13} = c_{51} e_{11} + c_{52} e_{22} + c_{53} e_{33} + 2 (c_{54} e_{23} + c_{55} e_{13} + c_{56} e_{12}),

6f

τ_{12} = c_{61} e_{11} + c_{62} e_{22} + c_{63} e_{33} + 2 (c_{64} e_{23} + c_{65} e_{13} + c_{66} e_{12}) .

In absence of inner heat source and body force the equation of motion are given as:

7a

τ_{11,1} + τ_{12,2} + τ_{13,3} = ρ {\ddot{u}}_{1},

7b

τ_{21,1} + τ_{22,2} + τ_{23,3} = ρ {\ddot{u}}_{2} - Ω^{2} u_{2} - 2 Ω {\dot{u}}_{3},

7c

τ_{31,1} + τ_{32,2} + τ_{33,3} = ρ {\ddot{u}}_{3} - Ω^{2} u_{3} + 2 Ω {\dot{u}}_{2} .

With the help of Eqs. (5) and (6), the equations of motions Eq. (7) become:

8a

(c_{11} u_{1,11} + c_{66} u_{1,22} + c_{55} u_{1,33}) + 2 (c_{16} u_{1,12} + c_{15} u_{1,13} + c_{56} u_{1,23}) + (c_{16} u_{2,11} + c_{26} u_{2,22} + c_{45} u_{2,33} + (c_{12} + c_{66}) u_{2,12} + (c_{14} + c_{56}) u_{2,13} + (c_{46} + c_{25}) u_{2,23}) + (c_{15} u_{3,11} + c_{46} u_{3,22} + c_{35} u_{3,33} + (c_{14} + c_{56}) u_{3,12} + (c_{13} + c_{55}) u_{3,13} + (c_{36} + c_{45}) u_{3,23}) - β_{11} θ_{, 1} = ρ {\ddot{u}}_{1},

8b

(c_{16} u_{1,11} + c_{26} u_{1,22} + c_{45} u_{1,33} + (c_{12} + c_{66}) u_{1,12} + (c_{14} + c_{56}) u_{1,13} + (c_{46} + c_{25}) u_{1,23}) + (c_{66} u_{2,11} + c_{22} u_{2,22} + c_{44} u_{2,33}) + 2 (c_{26} u_{2,12} + c_{46} u_{2,13} + c_{24} u_{2,23}) + (c_{56} u_{3,11} + c_{24} u_{3,22} + c_{34} u_{3,33} + (c_{46} + c_{25}) u_{3,12} + (c_{36} + c_{45}) u_{3,13} + (c_{23} + c_{44}) u_{3,23}) - β_{22} θ_{, 2} = ρ {\ddot{u}}_{2} - Ω^{2} u_{2} - 2 Ω {\dot{u}}_{3},

8c

(c_{15} u_{1,11} + c_{46} u_{1,22} + c_{35} u_{1,33} + (c_{14} + c_{56}) u_{1,12} + (c_{13} + c_{55}) u_{1,13} + (c_{36} + c_{45}) u_{1,23}) + (c_{56} u_{2,11} + c_{24} u_{2,22} + c_{34} u_{2,33} + (c_{46} + c_{25}) u_{2,12} + (c_{36} + c_{45}) u_{2,13} + (c_{23} + c_{44}) u_{2,23}) + (c_{55} u_{3,11} + c_{44} u_{3,22} + c_{33} u_{3,33}) + 2 (c_{45} u_{3,12} + c_{35} u_{3,13} + c_{34} u_{3,23}) - β_{33} θ_{, 3} = ρ {\ddot{u}}_{3} - Ω^{2} u_{3} + 2 Ω {\dot{u}}_{2} .

The generalized heat-conduction Eq. (2) is written as:

9

(k^{*} + k_{11} \frac{\partial}{\partial t}) θ_{, 11} + (k^{*} + k_{22} \frac{\partial}{\partial t}) θ_{, 22} + (k^{*} + k_{33} \frac{\partial}{\partial t}) θ_{, 33} = ρ c_{e} \ddot{θ} + θ_{0} (β_{11} {\ddot{u}}_{1,1} + β_{22} {\ddot{u}}_{2,2} + β_{33} {\ddot{u}}_{3,3}) .

The following non- dimensional variables are introduced to transform the above equations in non-dimensional form:

10

{x'}_{i} = \frac{1}{l} x_{i}, {u'}_{i} = \frac{c_{11}}{l β_{11} θ_{0}} u_{i}, t^{'} = \sqrt{\frac{c_{11}}{ρ}} \frac{1}{l} t, θ^{'} = \frac{θ}{θ_{0}}, c_{1}^{2} = \frac{c_{11}}{ρ}, Ω = \frac{c_{1}}{l} Ω^{'},

where $l$ is some standard length.

Using Eq. (10), the non dimensional forms of the Eqs. (8a)-(9) reduces to (omitting primes for convenience):

11a

(u_{1,11} + \frac{c_{66}}{c_{11}} u_{1,22} + \frac{c_{55}}{c_{11}} u_{1,33}) + 2 (\frac{c_{16}}{c_{11}} u_{1,12} + \frac{c_{15}}{c_{11}} u_{1,13} + \frac{c_{56}}{c_{11}} u_{1,23}) + (\frac{c_{16}}{c_{11}} u_{2,11} + \frac{c_{26}}{c_{11}} u_{2,22} + \frac{c_{45}}{c_{11}} u_{2,33} + (\frac{c_{12} + c_{66}}{c_{11}}) u_{2,12} + (\frac{c_{14} + c_{56}}{c_{11}}) u_{2,13} + (\frac{c_{46} + c_{25}}{c_{11}}) u_{2,23}) + (\frac{c_{15}}{c_{11}} u_{3,11} + \frac{c_{46}}{c_{11}} u_{3,22} + \frac{c_{35}}{c_{11}} u_{3,33} + (\frac{c_{14} + c_{56}}{c_{11}}) u_{3,12} + (\frac{c_{13} + c_{55}}{c_{11}}) u_{3,13} + (\frac{c_{36} + c_{45}}{c_{11}}) u_{3,23}) - θ_{, 1} = {\ddot{u}}_{1},

11b

(\frac{c_{16}}{c_{11}} u_{1,11} + \frac{c_{26}}{c_{11}} u_{1,22} + \frac{c_{45}}{c_{11}} u_{1,33} + (\frac{c_{12} + c_{66}}{c_{11}}) u_{1,12} + (\frac{c_{14} + c_{56}}{c_{11}}) u_{1,13} + (\frac{c_{46} + c_{25}}{c_{11}}) u_{1,23}) + (\frac{c_{66}}{c_{11}} u_{2,11} + \frac{c_{22}}{c_{11}} u_{2,22} + \frac{c_{44}}{c_{11}} u_{2,33}) + 2 (\frac{c_{26}}{c_{11}} u_{2,12} + \frac{c_{46}}{c_{11}} u_{2,13} + \frac{c_{24}}{c_{11}} u_{2,23}) + (\frac{c_{56}}{c_{11}} u_{3,11} + \frac{c_{24}}{c_{11}} u_{3,22} + \frac{c_{34}}{c_{11}} u_{3,33} + (\frac{c_{46} + c_{25}}{c_{11}}) u_{3,12} + (\frac{c_{36} + c_{45}}{c_{11}}) u_{3,13} + (\frac{c_{23} + c_{44}}{c_{11}}) u_{3,23}) - β_{2} θ_{, 2} = {\ddot{u}}_{2} - Ω^{2} u_{2} - 2 Ω {\dot{u}}_{3},

11c

(\frac{c_{15}}{c_{11}} u_{1,11} + \frac{c_{46}}{c_{11}} u_{1,22} + \frac{c_{35}}{c_{11}} u_{1,33} + (\frac{c_{14} + c_{56}}{c_{11}}) u_{1,12} + (\frac{c_{13} + c_{55}}{c_{11}}) u_{1,13} + (\frac{c_{36} + c_{45}}{c_{11}}) u_{1,23}) + (\frac{c_{56}}{c_{11}} u_{2,11} + \frac{c_{24}}{c_{11}} u_{2,22} + \frac{c_{34}}{c_{11}} u_{2,33} + (\frac{c_{46} + c_{25}}{c_{11}}) u_{2,12} + (\frac{c_{36} + c_{45}}{c_{11}}) u_{2,13} + (\frac{c_{23} + c_{44}}{c_{11}}) u_{2,23}) + (\frac{c_{55}}{c_{11}} u_{3,11} + \frac{c_{44}}{c_{11}} u_{3,22} + \frac{c_{33}}{c_{11}} u_{3,33}) + 2 (\frac{c_{45}}{c_{11}} u_{3,12} + \frac{c_{35}}{c_{11}} u_{3,13} + \frac{c_{34}}{c_{11}} u_{3,23}) - β_{3} θ_{, 3} = {\ddot{u}}_{3} - Ω^{2} u_{3} + 2 Ω {\dot{u}}_{2},

12

(ϵ_{3} + ϵ_{4} \frac{\partial}{\partial t}) θ_{, 11} + (ϵ_{3} + ϵ_{4} k_{2} \frac{\partial}{\partial t}) θ_{, 22} + (ϵ_{3} + ϵ_{4} k_{3} \frac{\partial}{\partial t}) θ_{, 33} = \ddot{θ} + (ϵ_{0} {\ddot{u}}_{1,1} + ϵ_{1} {\ddot{u}}_{2,2} + ϵ_{2} {\ddot{u}}_{3,3}),

where:

[ϵ_{0}, ϵ_{1}, ϵ_{2}] = \frac{β_{11} θ_{0}}{ρ c_{e} c_{11}} [β_{11}, β_{22}, β_{33}], [ϵ_{3}, ϵ_{4}] = \frac{1}{ρ c_{e}} [\frac{k^{*}}{c_{1}^{2}}, \frac{k_{11} c_{1}}{l}],

k_{2} = \frac{k_{22}}{k_{11}}, k_{3} = \frac{k_{33}}{k_{11}}, β_{2} = \frac{β_{22}}{β_{11}}, β_{3} = \frac{β_{33}}{β_{11}} .

Non – dimensional stress components can be calculated as:

13a

τ_{11} = \frac{1}{c_{11}} [c_{11} e_{11} + c_{12} e_{22} + c_{13} e_{33} + 2 (c_{14} e_{23} + c_{15} e_{13} + c_{16} e_{12})] - θ,

13b

τ_{22} = \frac{1}{c_{11}} [c_{21} e_{11} + c_{22} e_{22} + c_{23} e_{33} + 2 (c_{24} e_{23} + c_{25} e_{13} + c_{26} e_{12})] - β_{2} θ,

13c

τ_{33} = \frac{1}{c_{11}} [c_{31} e_{11} + c_{32} e_{22} + c_{33} e_{33} + 2 (c_{34} e_{23} + c_{35} e_{13} + c_{36} e_{12})] - β_{3} θ,

13d

τ_{23} = \frac{1}{c_{11}} [c_{41} e_{11} + c_{42} e_{22} + c_{43} e_{33} + 2 (c_{44} e_{23} + c_{45} e_{13} + c_{46} e_{12})],

13e

τ_{13} = \frac{1}{c_{11}} [c_{51} e_{11} + c_{52} e_{22} + c_{53} e_{33} + 2 (c_{54} e_{23} + c_{55} e_{13} + c_{56} e_{12})],

13f

τ_{12} = \frac{1}{c_{11}} [c_{61} e_{11} + c_{62} e_{22} + c_{63} e_{33} + 2 (c_{64} e_{23} + c_{65} e_{13} + c_{66} e_{12})] .

4. Normal mode analysis

The physical variables are decomposed in terms of normal modes to obtain the solution of (11) and (12) (Sarkar and Lahiri [13]) in the following form:

14

(u_{i}, θ, τ_{i j}) [x_{1}, x_{2}, x_{3}, t] = (u_{i}^{*}, θ^{*}, τ_{i j}^{*}) (x_{i}) e^{ω t + i (a x_{2} + b x_{3})},

where $i = \sqrt{- 1}$ , $ω$ being angular frequency and $a$ , $b$ are the wave numbers are $a$ and $b$ along $x_{2}$ and $x_{3}$ directions respectively.

Using Eq. (14) in Eqs. (11)-(13), we obtained (omitting ‘*’ for convenience):

15

u_{1,11} + a_{11} u_{1,1} + a_{12} u_{1} + a_{21} u_{2,11} + a_{22} u_{2,1} + a_{23} u_{2}

+ a_{31} u_{3,11} + a_{32} u_{3,1} + a_{33} u_{3} - θ_{, 1} = 0,

16

{b_{11} u}_{1,11} + b_{12} u_{1,1} + b_{13} u_{1} + u_{2,11} + b_{21} u_{2,1} + b_{22} u_{2}

+ b_{31} u_{3,11} + b_{32} u_{3,1} + b_{33} u_{3} - b_{34} θ_{, 1} = 0,

17

{m_{11} u}_{1,11} + m_{12} u_{1,1} + m_{13} u_{1} + m_{21} u_{2,11} + m_{22} u_{2,1}

+ m_{23} u_{2} + u_{3,11} + m_{31} u_{3,1} + m_{32} u_{3} - m_{33} θ_{, 1} = 0,

18

d_{41} u_{1,1} + d_{44} u_{2} + d_{46} u_{3} + d_{48} θ = θ_{, 11},

19

τ_{11} = u_{1,1} + h_{12} u_{2,1} + h_{13} u_{3,1} + h_{14} u_{1} + h_{15} u_{2} + h_{16} h_{3} - θ,

20

τ_{22} = h_{21} u_{1,1} + h_{22} u_{2,1} + h_{23} u_{3,1} + h_{24} u_{1} + h_{25} u_{2} + h_{26} u_{3} - β_{2} θ,

21

τ_{33} = h_{31} u_{1,1} + h_{32} u_{2,1} + h_{33} u_{3,1} + h_{34} u_{1} + h_{35} u_{2} + h_{36} u_{3} - β_{3} θ,

22

τ_{23} = h_{41} u_{1,1} + h_{42} u_{2,1} + h_{43} u_{3,1} + h_{44} u_{1} + h_{45} u_{2} + h_{46} u_{3},

23

τ_{13} = h_{51} u_{1,1} + h_{52} u_{2,1} + h_{53} u_{3,1} + h_{54} u_{1} + h_{55} u_{2} + h_{56} u_{3},

24

τ_{12} = h_{61} u_{1,1} + h_{62} u_{2,1} + h_{63} u_{3,1} + h_{64} u_{1} + h_{65} u_{2} + h_{66} u_{3},

where $a_{i j}$ , $b_{i j}$ , $m_{i j}$ , $d_{i j}$ and $h_{i j}$ $(i, j = 1, 2, 3)$ are given in Appendix I.

Equations (15)- (18) can be written in the vector- matrix differential equations (Sarkar and Lahiri [13]) as follows:

25

\frac{d \tilde{A}}{d x} = \tilde{A} \tilde{V},

where:

\tilde{V} = [u_{1}, u_{2}, u_{3}, θ, u_{1,1}, u_{2,1}, u_{3,1}, θ_{, 1}],

\tilde{A} = [\begin{matrix} L_{11} & L_{12} \\ L_{21} & L_{22} \end{matrix}],

where $L_{11}$ and $L_{12}$ are null matrix and identity matrix of order 4×4 and $L_{21}$ and $L_{22}$ are given in the Appendix I.

5. Solution of the vector- matrix differential equation: eigenvalue approach

Applying eigenvalue approach method as in Santra et al. [15] to solve the vector-matrix differential equation (25), we get the characteristic equation of the matrix $\tilde{A}$ as:

26

|\tilde{A} - λ I| = 0 .

The roots of the Eq. (26) are of the form:

λ = \pm λ_{i}, (i = 1,2, 3,4) .

The eigenvector $\tilde{X}$ corresponding to the eigenvalue $λ$ can be calculated as:

27

\tilde{X} = [\begin{matrix} δ_{1} = (f_{24} f_{13} - f_{14} f_{23}) (f_{22} f_{33} - f_{32} f_{23}) - (f_{34} f_{23} - f_{24} f_{33}) (f_{12} f_{23} - f_{22} f_{13}) \\ δ_{2} = (f_{34} f_{23} - f_{24} f_{33}) (f_{11} f_{23} - f_{21} f_{13}) - (f_{24} f_{13} - f_{14} f_{23}) (f_{21} f_{33} - f_{31} f_{23}) \\ \begin{matrix} δ_{3} = (f_{12} f_{21} - f_{11} f_{22}) (f_{21} f_{34} - f_{31} f_{24}) - (f_{22} f_{31} - f_{21} f_{32}) (f_{11} f_{24} - f_{14} f_{21}) \\ δ_{4} = (f_{11} f_{23} - f_{21} f_{13}) (f_{22} f_{33} - f_{32} f_{23}) - (f_{12} f_{23} - f_{22} f_{13}) (f_{21} f_{33} - f_{31} f_{23}) \\ \begin{matrix} {λ δ}_{1} \\ {λ δ}_{2} \\ \begin{matrix} {λ δ}_{3} \\ {λ δ}_{4} \end{matrix} \end{matrix} \end{matrix} \end{matrix}],

where $f_{i j}$ , $(i, j = 1, 2, 3)$ are given in the Appendix I.

The eigenvector ${\tilde{X}}_{i} [i = 1 (1) 8]$ corresponding to the eigenvalue $λ = λ_{i} [i = 1 (1) 8]$ can be calculated from equation (27). For our further reference, we use the following notations:

28

{\tilde{X}}_{i} = \{\begin{matrix} {[\tilde{X}]}_{λ = λ_{\frac{i + 1}{2}}}, i = 1 (2) 7, \\ {[\tilde{X}]}_{λ = λ_{- \frac{i}{2}}}, i = 2 (2) 8 . \end{matrix}

As in Lahiri et al. [12], the general solution of Eq. (25) which is regular as $x_{i} \to + \infty$ can be written as:

29

\tilde{V} = \sum_{i = 1}^{4} A_{i} {\tilde{X}}_{2 i} e^{- λ_{i} x_{1}}, x_{1} \geq 0,

where the arbitrary constants $A_{i}$ are to be determined from the boundary conditions of the problem and because of regularity condition of the solution at $+ \infty$ the terms containing exponential of growing nature in the space variables $x_{i}$ have been neglected.

Thus, the field variables can be written from the Eq. (29) for $x_{1} \geq 0$ as:

30

[u_{1}, u_{2}, u_{3}, θ] (x_{i}) = \sum_{i = 1}^{4} A_{i} {[δ_{1}, δ_{2}, δ_{3}, δ_{4}]}_{{λ = - λ}_{i}} e^{- λ_{i} x_{1}},

31

τ_{11} = \sum_{i = 1}^{4} [{(h_{14} - λ_{i}) δ_{1}|}_{{λ = - λ}_{i}} + {(h_{15} - λ_{i} h_{12}) δ_{2}|}_{{λ = - λ}_{i}} + {(h_{16} - λ_{i} h_{13}) δ_{3}|}_{{λ = - λ}_{i}} - {δ_{4}|}_{{λ = - λ}_{i}}] A_{i} e^{- λ_{i} x_{1}},

32

τ_{22} = \sum_{i = 1}^{4} [{(h_{24} - λ_{i} h_{21}) δ_{1}|}_{{λ = - λ}_{i}} + {(h_{25} - λ_{i} h_{22}) δ_{2}|}_{{λ = - λ}_{i}} + {(h_{26} - λ_{i} h_{23}) δ_{3}|}_{{λ = - λ}_{i}} - {β_{2} δ_{4}|}_{{λ = - λ}_{i}}] A_{i} e^{- λ_{i} x_{1}},

33

τ_{33} = \sum_{i = 1}^{4} [{(h_{34} - λ_{i} h_{31}) δ_{1}|}_{{λ = - λ}_{i}} + {(h_{35} - λ_{i} h_{32}) δ_{2}|}_{{λ = - λ}_{i}} + {(h_{36} - λ_{i} h_{33}) δ_{3}|}_{{λ = - λ}_{i}} - {β_{3} δ_{4}|}_{{λ = - λ}_{i}}] A_{i} e^{- λ_{i} x_{1}},

34

τ_{23} = \sum_{i = 1}^{4} [{(h_{44} - λ_{i} h_{41}) δ_{1}|}_{{λ = - λ}_{i}} + {(h_{45} - λ_{i} h_{42}) δ_{2}|}_{{λ = - λ}_{i}} + {(h_{46} - λ_{i} h_{43}) δ_{3}|}_{{λ = - λ}_{i}}] A_{i} e^{- λ_{i} x_{1}},

35

τ_{13} = \sum_{i = 1}^{4} [{(h_{54} - λ_{i} h_{51}) δ_{1}|}_{{λ = - λ}_{i}} + {(h_{55} - λ_{i} h_{52}) δ_{2}|}_{{λ = - λ}_{i}} + {(h_{56} - λ_{i} h_{53}) δ_{3}|}_{{λ = - λ}_{i}}] A_{i} e^{- λ_{i} x_{1}},

36

τ_{12} = \sum_{i = 1}^{4} [{(h_{64} - λ_{i} h_{61}) δ_{1}|}_{{λ = - λ}_{i}} + {(h_{65} - λ_{i} h_{62}) δ_{2}|}_{{λ = - λ}_{i}} + {(h_{66} - λ_{i} h_{63}) δ_{3}|}_{{λ = - λ}_{i}}] A_{i} e^{- λ_{i} x_{1}} .

6. Boundary conditions

To determine the arbitrary constants $A_{i}$ , boundary conditions are considered at the surface on the half space $x_{1} = 0$ as in Sarkar and Lahiri [13].

Mechanical boundary condition: On the traction, free boundary of the half-space:

37

x_{1} = 0, τ_{11} (0, x_{2}, x_{3}, t) = τ_{22} (0, x_{2}, x_{3}, t) = τ_{33} (0, x_{2}, x_{3}, t) = 0 .

Thermal boundary condition:

38

q_{n} + ν θ = r (0, x_{2}, x_{3}, t) .

Since, $q_{n} = - \partial θ / \partial n$ , we get $ν θ^{*} - \partial θ / \partial x_{1} = r^{*}$ at $x_{1} = 0$ , where $q_{n}$ is the normal components of the heat flux vector, $ν$ is the Biot’s number, $ν \to 0$ corresponding thermally insulated boundary, $ν \to + \infty$ corresponding to isothermal boundary. $r (0, x_{2}, x_{3}, t)$ is the intensity of the applied heat source.

With the help of Eq. (14), Eqs. (37) and (38) become (omitting ‘*’ for convenience):

τ_{11} (0, x_{2}, x_{3}, t) = τ_{22} (0, x_{2}, x_{3}, t) = τ_{33} (0, x_{2}, x_{3}, t) = 0,

ν θ - \frac{\partial θ}{\partial x_{1}} = 0, x_{1} = 0 .

7. Numerical analysis

For the purpose of illustrating the problem, we now consider a numerical example for which computational results are presented. Since $ω$ is complex, we take $ω = ω_{0} + i ς$ , for studying the effect of wave propagation, we use the following physical parameters in SI units given in the following.

The numerical constants are given by:

c_{11} = 16.248 GPa, c_{14} = - 1.152 GPa, c_{25} = 1.608 GPa, c_{22} = 11.88 GPa,

c_{15} = 0 GPa, c_{26} = 1.248 GPa, c_{33} = 12.216 GPa, c_{16} = 0.561 GPa,

c_{32} = 1.032 GPa, c_{12} = 1.48 GPa, c_{21} = 1.48 GPa, c_{34} = 0.672 GPa,

c_{13} = 2.4 GPa, c_{23} = 1.032 GPa, c_{35} = 0.216 GPa, c_{41} = - 1.152 GPa,

c_{24} = 0.912 GPa, c_{36} = 0.216 GPa, c_{42} = 0.912 GPa, c_{51} = 0 GPa,

c_{61} = 0.561 GPa, c_{43} = - 0.672 GPa, c_{52} = 1.608 GPa, c_{62} = 1.248 GPa,

c_{44} = 5.64 GPa, c_{53} = 0.216 GPa, c_{63} = - 0.216 GPa, c_{45} = 2.16 GPa

c_{54} = 2.16 GPa, c_{64} = 0 GPa, c_{46} = 0 GPa, c_{55} = 5.88 GPa, c_{65} = 0 GPa,

c_{56} = 0 GPa, c_{66} = 6.91 GPa, c_{E} = 0.787, β_{11} = 7.042, β_{11} = 7.046,

β_{11} = 6.09, k_{11} = 0.0921, k_{11} = 0.0963, k_{11} = 0.0917, θ_{0} = 293 .

Variations of the stress components and temperature distribution has been graphically shown from Fig. 1 to Fig. 7 for G-N model of type III comparing with G-N model of type II with rotation and without rotation with respect to $x_{1}$ for the constant values of $t =$ 0.5 and $ω =$ 0.2.

(1) The nature of the stress component $τ_{11}$ is contraction in nature for G-N model of type II and III with rotation $Ω =$ 25 whereas without rotation stress is parallel to the $x_{1}$ axis. Stresses for G-N model type II and III are same and parallel in $0 < x_{1} < 3$ and then gradually decreasing.

(2) Fig. 2 shows that the stress component $τ_{22}$ is extensive in nature. The maximum value occurs for G-N model of type III with rotation. Stresses are gradually increasing in $0 < x_{1} < 0.2$ and then decreasing.

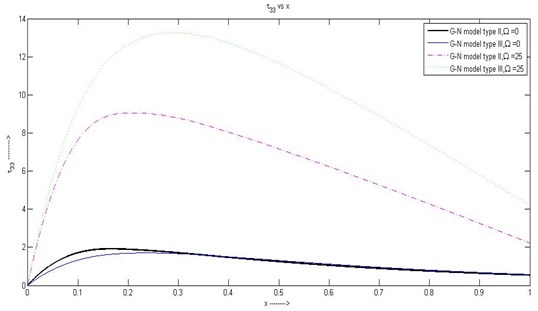
(3) Nature of the stress $τ_{33}$ is same as $τ_{22}$ .

Fig. 1Variation of τ11 with respect to x1 with rotation and without rotation

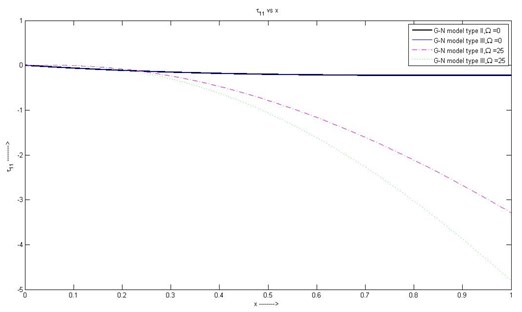
Fig. 2Variation of τ22 with respect to x1 with rotation and without rotation

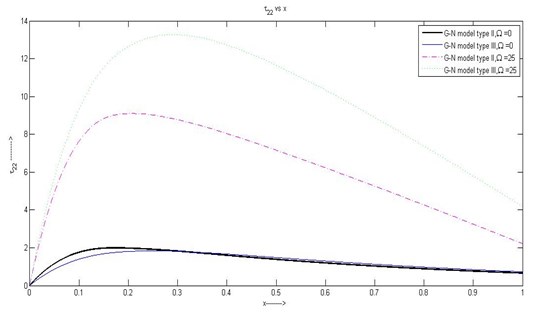
Fig. 3Variation of τ33 with respect to x1 with rotation and without rotation

(4) In Fig. 4 nature of the stress component $τ_{12}$ is same for G-N model II and III without ritation. Small variation can be seen for the case of with rotation in the range $0 < x_{1} < 0.2$ . and then stresses are gradually decreasing for all the four cases.

(5) In Fig. 5 nature of $τ_{13}$ is same as $τ_{12}$ for the case of without rotation. And for the case of with rotation the stresses are parallel to the $x_{1}$ axis except for a small variation in the range $0.3 < x_{1} < 0.5$ in case of G-N model type III.

Fig. 4Variation of τ12 with respect to x1 with rotation and without rotation

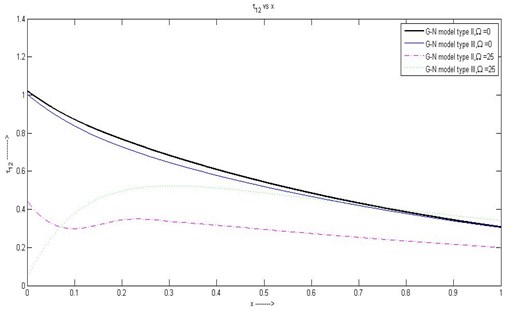
Fig. 5Variation of τ13 with respect to x1 with rotation and without rotation

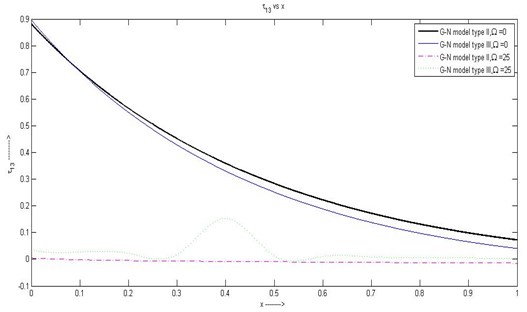
Fig. 6Variation of τ23 with respect to x1 with rotation and without rotation

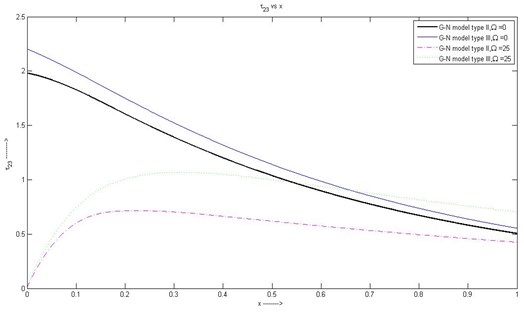
(6) Fig. 6 shows that initial value of $τ_{23}$ for G-N model type II and III with rotation is 0 for $x_{1} = 0$ whereas without rotation the initial values are 2 and 2.2 for G-N model II and III respectively. In the range $0 < x_{1} < 1$ , the stress component $τ_{23}$ monotonically decreases without rotation whereas it increases initially starting from 0, attains a maximum value and then gradually decreases $x_{1} > 0.3$ with rotation.

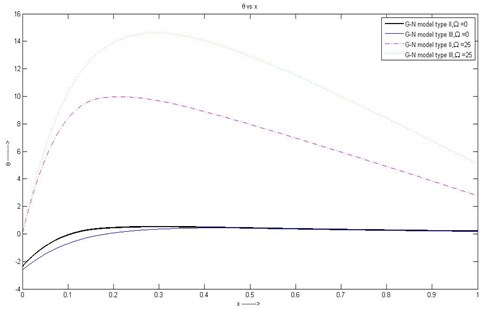
(7) From Fig. 7 we can see that the temperature is gradually increasing in $0 < x_{1} < 0.2$ and then maximum value occurs at $x_{1} =$ 0.2 for the case of G-N model type III with rotation and after that temperature for all the four cases are gradually decreasing.

Fig. 7Variation of θ with respect to x1 with rotation and without rotation

8. Conclusions

Thermal stresses and temperature on a traction free boundary in a half space for G-N model type II as well as type III due to time dependent heat source shows significant dependence on rotation as evident from the above curves.

Various stress components deviate under rotation from their rotation less counter parts. Certain stress component possesses non zero initial value when subject to rotation whereas for temperature a converse effect has been found.

References

Biot M. A. Thermoelasticity and irreversible thermodynamics. Journal of Applied Physics, Vol. 27, 1956, p. 240-253.

Publisher
Ignaczak J. Uniqueness in generalized thermoelasticity. Journal of Thermal Stresses, Vol. 2, 1979, p. 171-175.

Publisher
Dhaliwal R. S., Sherief H. H. Generalized thermoelasticity for anisotropic media. Quarterly of Applied Mathematics, Vol. 33, 1980, p. 1-8.

Publisher
Ignaczak J. A note on uniqueness in thermoelasticity with one relaxation time. Journal of Thermal Stresses, Vol. 5, 1982, p. 257-263.

Publisher
Pal P. K., Acharya D. Effect of inhomogeneity on the surface waves in anisotropic media. Sadhana, Vol. 23, 1998, p. 247-258.

Publisher
Green A. E., Naghdi P. M. A re-examination of the basic postulate of thermomechanics. Proceedings of the Royal Society of London A, Vol. 432, 1991, p. 171-194.

Publisher
Green A. E., Naghdi P. M. On undamped heat waves in an elastic solid. Journal of Thermal Stresses, Vol. 15, 1992, p. 253-264.

Publisher
Green A. E., Naghdi P. M. Thermoelasticity without energy dissipation. Journal of Elasticity, Vol. 31, 1993, p. 189-208.

Publisher
Kar A., Kanoria M. Thermoelastic interaction with energy dissipation in an infinitely extended thin plate containing a circular hole. Far East Journal of Applied Mathematics, Vol. 24, 2006, p. 201-217.

Search CrossRef
Youssef H. M. On a theory of two temperature – generalized thermoelasticity. IMA Journal of Applied Mathematics, Vol. 71, 2006, p. 383-390.

Publisher
Abd-Alla A. M., Abo-Dahab S. M. Time-harmonic sources in a generalized magnetothermoviscoelastic continuum with and without energy dissipation. Applied Mathematical Modeling, Vol. 33, 2009, p. 2388-2402.

Publisher
Lahiri A., Das N. C., Sarkar S., Das M. Matrix method of solution of coupled differential equations and its application to generalized thermoelasticity. Bulletin of Calcutta Mathematical Society, Vol. 101, 2009, p. 571-590.

Search CrossRef
Sarkar N., Lahiri A. A three dimensional thermoelastic problem for a half- space without energy dissipation. International Journal of Engineering Science, Vol. 51, 2012, p. 310-325.

Publisher
Pal P. C., Kumar S., Mandal D. Wave propagation in an inhomogeneous anisotropic generalized thermoelastic solid. Journal of Thermal Stresses, Vol. 37, 2014, p. 817-831.

Publisher
Santra S., Das N. C., Kumar R., Lahir A. Three dimensional fractional order generalized thermoelastic problem under effect of rotation in a half space. Journal of Thermal Stresses Vol. 38, 2015, p. 309-324.

Publisher

Cited by

Active noise control method of power communication signal based on BP neural network

Dongbing Yuan | Yue Zhang

(2022)

A Study on the Generalized Thermoelastic Problem for an Anisotropic Medium

Debkumar Ghosh | Abhijit Lahiri

(2018)

About this article

Received

29 December 2016

Accepted

18 January 2017

Published

30 June 2017

DOI

https://doi.org/10.21595/mme.2017.18143

Keywords

anaisotropic half space

G-N model II and III

normal mode analysis

eigenvalue approach

Acknowledgements

The authors are thankful to DST-Purse Programme of the Department of Mathematics, Jadavpur University, Kolkata 700032.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous

Research article

2022 11 03

Eigen value approach with memory dependant derivative on homogeneous isotropic infinitely extended rotating plate of a finite thickness in absence of heat source

S. Chakraborty, A. Lahiri, B. Das

Research article

2022 06 30

Dual-phase-lag model on microelongated thermoelastic rotating medium

Mohamed I. A. Othman, Sarhan Y. Atwa, E. E. M. Eraki, Mohamed F. Ismail

Research article

2019 09 30

Thermal shock behaviour on generalized thermoelastic semi-infinite medium with moving heat source under Green Naghdi-III model

Biswajit Singh, Smita Pal (Sarkar)

Research article

2017 06 30

Two-dimensional generalized thermo-elastic problem for anisotropic half-space

Debkumar Ghosh, Abhijit Lahiri, Ibrahim A. Abbas

S. Santra, A. Lahiri, and N. C. Das, “Dynamic problem in 3D thermoelastic half-space with rotation in context of G-N type II and type III,” Mathematical Models in Engineering, Vol. 3, No. 1, pp. 58–70, Jun. 2017, https://doi.org/10.21595/mme.2017.18143

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/mme.2017.18143
UR  - https://doi.org/10.21595/mme.2017.18143
TI  - Dynamic problem in 3D thermoelastic half-space with rotation in context of G-N type II and type III
T2  - Mathematical Models in Engineering
AU  - Santra, S.
AU  - Lahiri, A.
AU  - Das, N. C.
PY  - 2017
DA  - 2017/06/30
PB  - JVE International Ltd.
SP  - 58-70
IS  - 1
VL  - 3
SN  - 2351-5279
SN  - 2424-4627
ER  - 

Copy Ris

Copied to clipboard!

@article{Santra_2017,
	doi = {10.21595/mme.2017.18143},
	url = {https://doi.org/10.21595/mme.2017.18143},
	year = 2017,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {3},
	number = {1},
	pages = {58--70},
	author = {S. Santra and A. Lahiri and N. C. Das},
	title = {Dynamic problem in 3D thermoelastic half-space with rotation in context of G-N type {II} and type {III}},
	journal = {Mathematical Models in Engineering}
}

Copy Bibtex

Copied to clipboard!

[1]S. Santra, A. Lahiri, and N. C. Das, “Dynamic problem in 3D thermoelastic half-space with rotation in context of G-N type II and type III,” Mathematical Models in Engineering, vol. 3, no. 1, pp. 58–70, Jun. 2017, doi: 10.21595/mme.2017.18143.

Copy IEEE

Copied to clipboard!

Santra, S., A. Lahiri, and N. C. Das. “Dynamic Problem in 3D Thermoelastic Half-Space with Rotation in Context of G-N Type II and Type III.” Mathematical Models in Engineering 3, no. 1 (June 30, 2017): 58–70. https://doi.org/10.21595/mme.2017.18143.

Copy Chicago

Copied to clipboard!

Dynamic problem in 3D thermoelastic half-space with rotation in context of G-N type II and type III

Abstract

1. Introduction

2. Basic equations

3. Formulation of the problem

4. Normal mode analysis

5. Solution of the vector- matrix differential equation: eigenvalue approach

6. Boundary conditions

7. Numerical analysis

8. Conclusions

References

Cited by

About this article

Related Articles