Abstract
Customers call for better performance, such as miniaturization, low noise, and higher load capacity of gear system. The micro-segment gear is a new tooth form whose tooth profile curve is composed of many micro segments. This paper investigates the bifurcation and chaos characteristics of spur micro-segment gear pair. To improve the authenticity of the solution, the time-varying mesh stiffness is expressed in term of piecewise function, and the normal profile deviation is expressed in the form of Fourier series. The influence of damping coefficient, excitation frequency, internal and external excitation on bifurcation and chaos properties of the system are analyzed. The numerical results show that the dynamic system is very sensitive to damping coefficient. With the increasing of damping coefficient, the number of bifurcation and impressive jump tends to decrease; and the intervals of dimensionless frequency leading to unstable or chaotic motion have a trend to concentration. The influence of external and internal excitation on bifurcation characteristics are also investigated. Comparison results show that, internal excitation has a greater effect than external excitation based on corresponding amplitude-frequency diagrams and bifurcation diagrams.
1. Introduction
Gears are the indispensable components of industrial machinery, automobile, ship, locomotive, airplane, and other machines. The customers require higher load capacity, rotating speed, power-weight ratio, lower vibration and noise of gearing.
Involute gears have been investigated systematically and comprehensively since 1694. The involute gear driving thus has developed to be the most important mechanical transmission gradually. Modern industry requires gears to implement miniaturization, as well as to improve power-weight ratio. Consequently, the shortages, such as relative sliding, convex-convex pattern of contact and minimum tooth number for gears without undercut, make involute gear difficult to meet the needs of modern industry equipment.
Relative sliding leads to friction loss between the contact teeth directly. The convex-convex contact pattern reduces contact strength. This effect is more significant as the rotating speed and load increases. The minimum tooth number for gears without undercut prevents the miniaturization of the system.
To overcome these shortages, Komori [1-3] proposed a new type of high strength gear profile named LogiX gear in 1980’s whose tooth profile is composed of many micro involute segments. The LogiX tooth profile has been known as that having concave-convex pattern of contact like W-N (Wildhaber-Novikov) tooth profile and the improvements are LogiX tooth profile can be applied to a spur/helical gear and have a feature of line-contact. While, Komori didn’t point out any actual application of this type of gearing could be limited by the processing problem.
Actually, in NC (numerical control) machining, computerized interpolation is employed in producing plane, cylinder or complex curved surface. A final tooth profile is composed of a large number of segments and the final profile will be closer to the designed position with an increase in the quantity of micro segment. Inspired by the NC machining technology and the design strategies of LogiX gear, Han proposed a new tooth profile named micro-segment tooth profile. By employing micro segments to replace micro involutes, a micro-segment gear can be easier processed in NC machining centers [4]. The author has carried out theoretical and experimental researches of micro-segment in his PhD dissertation. The basic characteristics such as strength problem were researched; the effect of primary parameters on tooth profile shape was discussed; and the hob cutter was designed [5]. The studies on the temperature rise comparison [6], transmission efficiency calculation [7] and strength [5] show that micro-segment gear has better static performance than involute gear.
Dynamic analysis is an effective method of predicting the system’s performance. Over the past few decades, a lot of researches have been conducted on gear dynamics [8-22], while most of them are centered on involute gears. Several of these studies are associated with non-involute gear according to available literature. [23] developed a dynamic model of a single-stage cycloid drive and considered the dynamic behavior of cycloid planetary gear trains. [24] investigated the approach on parametric modeling and dynamic contact analysis of non-involute beveloid gears which have advantages of relieving the high dynamic stress and contact shock problem of intersecting axes beveloid gear pairs. Recently, we employed the single-degree-of-freedom (SDOF) model for micro-segment gear transmission with a small change [25]; the profile deviation between micro-segment and involute gear is regarding as the displacement excitation. Time-varying mesh stiffness is calculated by finite element method. In reference [25], three working conditions were assumed to explore the difference between two kinds of tooth profile, and the contrast analysis result was shown that the micro-segment gear has a better dynamic performance in high-speed and heavy load condition.
In this paper, the bifurcation and chaos characteristic will be explored. The influence of mesh frequency, internal and external excitation will be investigated mainly. We have great expectations to lay a foundation for micro-segment gear dynamic theoretical system.
2. Dynamic model for micro-segment gear
The constructing principle, presented in Appendix A1, indicated that, each micro segment involute (simplified as straight line finally) has its own base circle, and they are disciplinary changing from one micro segment to the next one, while the involute tooth profile has an invariable base circle. The feature of changing base circle means changing line of action and direction of mesh force. Thus, it is unacceptable to use the SDOF model directly. Here, an adjustment has been made to let the SODF model suit for micro-segment gear, i.e. the tooth profile deviation between micro-segment gear and involute gear is considered as another displacement excitation.
2.1. Mathematical representation of dynamic model for micro-segment gear pair
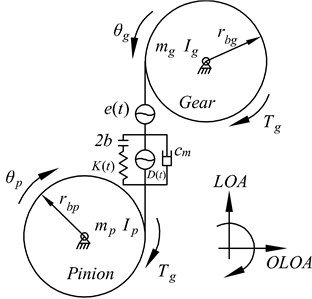
The mechanical model is shown in Fig. 1. Two gears are combined with supporting shafts, which are regarded as rigid bodies with large support stiffness. The pinion and gear are represented by their base circles with radius rbp and rbg, respectively. The equations of motion can be expressed as:
where, Ip and Ig are polar mass moments of inertia. mp and mg are masses. K(t) is time-varying mesh stiffness. cm=2ζ√km/(1/mp+1/mg) is viscous damping. D(t) is time-varying profile deviation of micro-segment gear comparing with involute gear. The static transmission error e(t) is regarded as internal excitation which can be expressed in a Fourier series in the form:
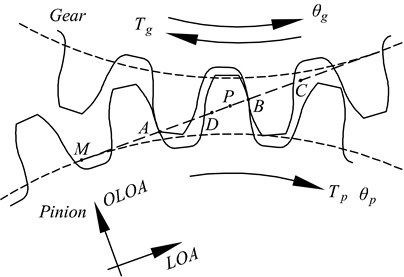
Fig. 1a) Snap shot of contact pattern (at t= 0) of a spur micro-segment gear pair; b) the non-linear dynamic model
a)
b)
The external excitations TP and Tg are acting on the pinion and gear which can be decomposed into average torque Tm and fluctuating external torque excitation T(t). To simplify the calculation, the fluctuation of output torque is neglected, i.e. Tg=Tgm and input torque can be expressed via Fourier series as:
The backlash function h is usually calculated by:
By employing a composite co-ordinate:
Eq. (1) can be re-formed as:
with:
where me is the equivalent mass. Fm is average force and Fp(t) is the fluctuating force related to external torque excitation. Fe(t) is the fluctuating force related to internal displacement excitation.
2.2. Two important parameters in dynamic model (K(t),D(t))
The main difference between proposed dynamic model and the traditional SDOF is embodied in two important parameters K(t) and D(t).
2.2.1. Time-varying mesh stiffness K(t)
The time-varying mesh stiffness greatly affects the dynamics of gear system. According to the available literature, the mesh stiffness is usually simplified or calculated by the empirical equations. These methods are often based on the classical theory of elasticity and numerical approaches. However, it is considered to be unsuitable to use these methods on the dynamic research of micro-segment gear due to the special profile. Therefore, the finite element method is utilized to calculate the mesh stiffness. With the design parameters of micro-segment gears listed in table 1, the 3D finite element model for a pair of tooth of micro-segment gear is shown in Fig. 2.
Fig. 2The entity model of micro-segment gear
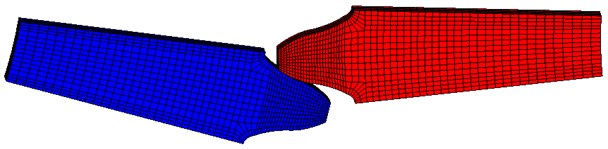
The 3D finite element model contains about 9840 elements and the tooth thickness in mesh model is set to 1mm. Four end faces and one cylindrical face are fixed, and the other cylindrical face is defined as the loading surface. Since the gear meshing is a nonlinear process, the contact surfaces are defined as nonlinear contacting to get a more realistic result.
Table 1Common design parameters of the spur gear pairs
Parameter | Pinion/Gear |
Number of teeth | 45 |
Transverse module (mm) | 2 |
Width (mm) | 20 |
Mass (kg) | 0.885 |
Moments of inertia (kg∙m2) | 9.988e-004 |
Density (kg/m3) | 9860 |
Elasticity modulus (GPa) | 205 |
Poisson ratio | 0.3 |
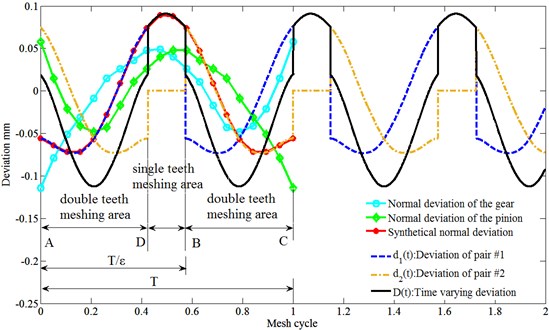
In the meshing process of a gear set with a contact ratio εlower than 2, we can conceptually consider that there are always two pairs of teeth (pair #1 and pair #2) under contact. In Fig. 1(a), the meshing teeth pair with contact point located between point A and point B is defined as pair #1, and the meshing teeth pair with contact point located between point B and point C is defined as pair #2.
Fig. 3The mesh stiffness of micro-segment gear
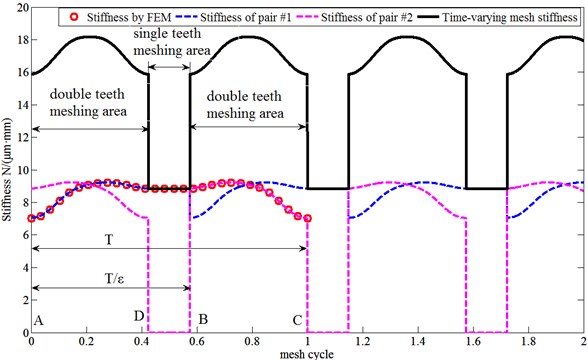
The mesh stiffness for a pair of teeth from A to C, can be calculated by the FEM mentioned above, and can be expressed in the form of Fourier series expansion as follow:
where km is average mesh stiffness. kaj, kbj are amplitudes of the jth order harmonic. wk is fitting frequency; then we have T=2π/wk, here T is the period of the mesh stiffness k(t) for one pair of teeth, rather than the time-varying mesh stiffness for the gear set. A good fit can be achieved with the first eight orders of the Fourier series, as show in Fig. 3 and fitting parameters are listed in Table 2.
Table 2Fitting parameters of stiffness (Nμm-1 mm-1) and synthetically normal deviation (mm)
j | kaj | kbj | daj | dbj |
1 | –6.541e-1 | –2.101e-4 | –8.088e-2 | 1.733e-05 |
2 | –6.419e-1 | –2.997e-4 | 2.627e-2 | –3.418e-05 |
3 | –2.142e-1 | –1.55e-4 | 6.399e-3 | 5.01e-05 |
4 | –6351e-2 | –6.556e-05 | 7.992e-4 | –6.465e-05 |
5 | –4.607e-2 | –6.824e-05 | 9.012e-4 | 7.744e-05 |
6 | 1.491e-2 | 2.454e-06 | 3.851e-4 | –8.812e-05 |
7 | 1.028e-2 | 1.405e-05 | 1.61e-4 | 9.64e-05 |
8 | 8.566e-3 | –7.323e-07 | 6.113e-4 | –0.000102 |
km | 8.622 | / | ||
dm | / | –0.01078 | ||
Then, the time-varying mesh stiffness can be obtained by summing the stiffness of pair #1 and pair #2, as show in Fig. 3. According to Fig. 3, it can be found that the frequency of time-varying mesh stiffness function is εwe, and the piecewise stiffness functions can be expressed as:
={km+∑8j=1(kajcos(jωk(mod(t,Tε)+Tε))+kbjsin(jωk(mod(t,Tε)+Tε))),0≤mod(t,T)<Tε-Tε,0,Tε-Tε≤mod(t,T)<Tε,
={k(mod(t,Tε)+Tε)+k(mod(t,Tε)),0≤mod(t,Tε)<Tε-Tε,k(mod(t,Tε)),Tε-Tε≤mod(t,Tε)<Tε,
={2km+∑8j=1(kajcos(jωk(mod(t,Tε)+Tε))+kbjsin(jωk(mod(t,Tε)+Tε)))+∑8j=1(kajcos(jωkmod(t,Tε))+kbjsin(jωkmod(t,Tε))),0≤mod(t,Tε)<Tε-Tε,km+∑8j=1(kajcos(jωkmod(t,Tε))+kbjsin(jωkmod(t,Tε))),Tε-Tε≤mod(t,Tε)<Tε.
2.2.2. Time-varying profile deviation D(t)
The normal deviation of micro-segment gear compared with the standard involute profile will be analyzed in this section. In Fig. 4, the geometric models of the single tooth for both micro-segment gear and standard involute gear are established. It is clear that these two profiles are obviously different.
Fig. 4The geometric models for both micro-segment gear and standard involute gear
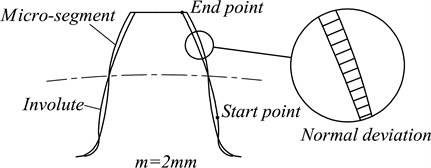
To research the influence of different profiles on the dynamic characteristics of the gear system, the magnitude of deviation should be accurately expressed. In the process of meshing for a pair of teeth, the contact point of the pinion moves from start point to end point and the corresponding point in the gear moves from end point to start point. This process is divided into many small sections in terms of angle, and each micro-angle corresponds to a normal deviation, as show in Fig. 4. Due to the cooperative working of two gears, the displacement excitation of profile deviation d(t) should be the normal resultant for both of the gear and pinion body in Fig. 5.
Identical to the time-varying mesh stiffness, the synthetically normal deviation of a pair of teeth also can be expressed as following Fourier series expansion, the fitting parameters are also listed in Table 2:
where dm is average deviation of synthetically normal deviation. daj, dbj are amplitudes of the jth order harmonic. The time-varying profile synthetize deviation for the example system is also a piecewise function which can be expressed as follow:
={2dm+∑8j=1(dajcos(jωk(mod(t,Tε)+Tε))+dbjsin(jωk(mod(t,Tε)+Tε)))+∑8j=1(dajcos(jωkmod(t,Tε))+dbjsin(jωkmod(t,Tε))),0≤mod(t,Tε)<Tε-Tε,dm+∑8j=1(dajcos(jωkmod(t,Tε))+dbjsin(jωkmod(t,Tε))),Tε-Tε≤mod(t,Tε)<Tε.
As shown in Fig. 5, the time-varying deviation curve is not continuous at the critical point of single and double teeth contact area, i.e., point D and point B. However, Fe(t) is composed of the second derivative of e(t) and D(t) which means D(t) should be expressed as a continuous differentiable formula. Thus, a further Fourier transform could be more than sufficient.
2.2.3. Nondimensionalization of the dynamic differential equation
As usual, the vibration differential equation of the gear system is processed to be dimensionless to assure the equation don’t depend on the specific physical dimension. Dimensionless equation of motion can be obtained by defining:
Fig. 5The time-varying normal deviation of micro-segment gear compared with standard involute gear
Then the original equation of motion Eq. (6) can eventually be put in the normalized form:
+∑∞r=1(rΩe)2¯ercos(rwet+φer)-¨ˉD(τ),
where:
3. Numerical results and discussion
The dynamic performances of a geared system are much effected by the mesh frequency, internal excitation and external excitation. Moreover, these excitations are obviously different in the bifurcation characteristics.
3.1. Influence of excitation frequency
Following parameters are adopted in this section: the amplitudes of internal excitation ˉer=0; the external excitation is neglected here and average torque is controlled by input power P=200 KW [26]; the backlash b=20 μm.
The dimensionless nonlinear dynamic Eq. (13) of micro-segment gear system with time-varying stiffness, profile deviation and backlash is solved using the fourth order Runge-Kutta method. The simulations run for 20,000 periods and only the data of the last 10-20 periods are plotted to guarantee the data relates to steady state conditions. Then the sampled data is used to generate the bifurcation diagram, times history chart, phase diagram, Poincare map and FFT spectrogram of micro-segment gear system in order to obtain an intuitive understanding of the dynamic behaviors.
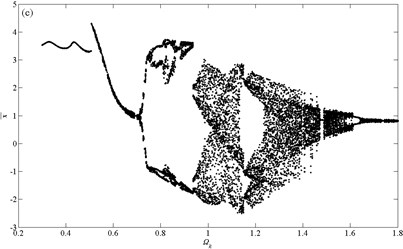
Fig. 6 presents four bifurcation diagrams for dimensionless dynamic transmission error of micro-segment gear system using dimensionless mesh frequency Ωk as bifurcation parameter. It can be observed that damping coefficient has a great effect on bifurcation behaviors of the gear system. The jump phenomena and chaotic area change much as damping coefficient increases.
Fig. 6Bifurcation diagrams using Ωk as bifurcation parameter: a) ζ= 0.06; b) ζ= 0.08; c) ζ= 0.1; d) ζ= 0.12

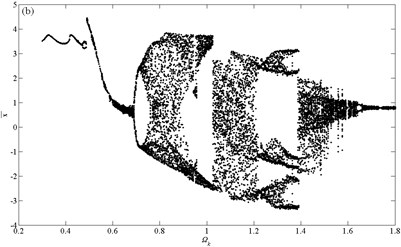
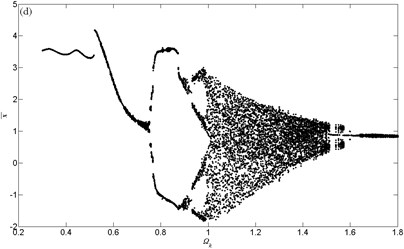
The bifurcation characteristic for the case of ζ=0.06 is shown in Fig. 6(a). It can be found that the motion is non-harmonic-single-periodic (NHS-periodic) at low values of dimensionless mesh frequency, i.e. Ωk≤0.446. The response period T of time history chart equals to excitation period, the phase diagram is a closed non-circle and non-elliptic curve, the resulting trace in Poincare map is a dot and the discrete points locate at the frequencies of mfk (where, m is a positive integer, fk=Ωk/2π, similarly hereinafter) in corresponding FFT Spectrogram according to Fig. 7(a). In the meantime, the first distinct amplitude jump happens at Ωk=0.41.
Fig. 7Simulation results for some important values of Ωk when ζ=0.06: a) NHS-periodic at Ωk=0.25; b) 2T-periodic at Ωk=0.45; c) NHS-periodic at Ωk=0.552; d) 2T-periodic at Ωk=0.668; e) chaotic at Ωk=0.72; f) 3T-periodic at Ωk=0.752; g) 2T-periodic at Ωk=1.182; h) 3T-peiodic at Ωk=1.38; i) 2T-periodic at Ωk=1.67; j) simple harmonic at Ωk=1.74
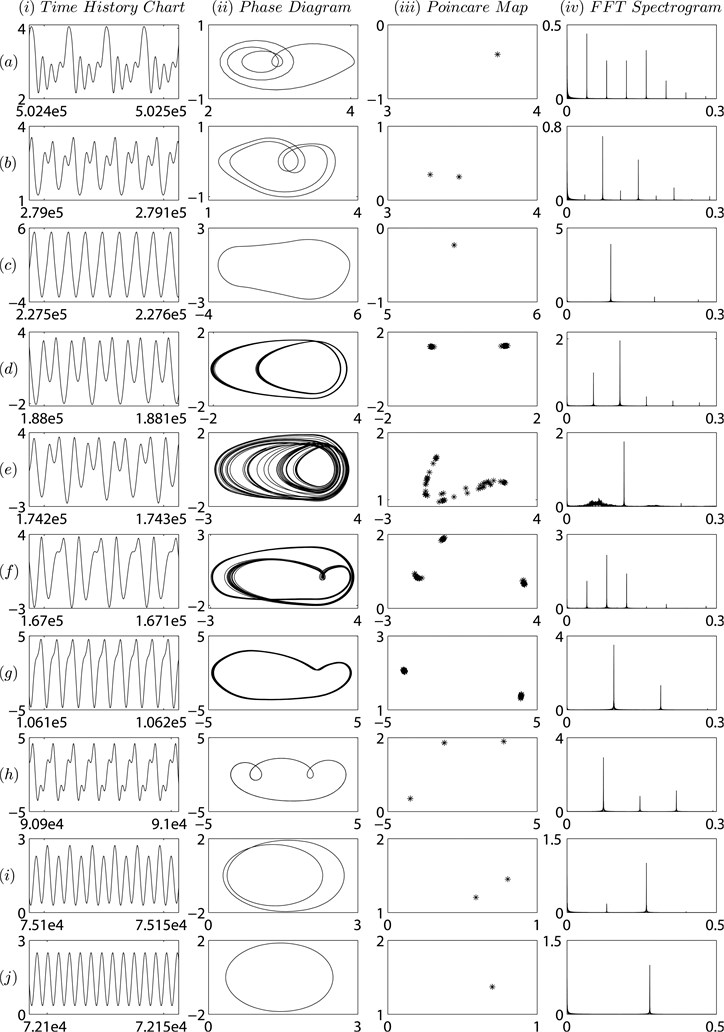
The motion mutates to be 2T-periodic as Ωk reaches 0.448 and this status continues to Ωk=0.464, as shown in Fig. 7(b), the dominant peaks in FFT Spectrogram are ifk/2, where, i is an even number. The frequency jfk/2, where j is an odd number, lead to two deflected and closed cures in phase diagram. After the second jump at Ωk=0.464, the system comes to be repeatedly transform between NHS-periodic and 2T-periodic motion until Ωk gets 0.492. The NHS-periodic motion lasts to Ωk=0.66 and the third jump occurs at Ωk=0.604.
As the dimensionless frequency Ωk further increases, the dynamic behavior of the system reverts to a 2T-periodic motion again at 0.662≤Ωk≤0.682. Here, two closed curves appear in the phase diagram and the dominant peaks in FFT Spectrogram are mfk/2 which is different with the formal 2T-periodic motion.
After that, the motion evolves to be unstable, even chaotic in the range of 0.684≤Ωk≤0.738. When the dimensionless frequency ran up to 0.74, the system exhibits 3T-periodic motion, as shown in Fig. 7(f), the trajectories repeat themselves every three periods, and there are three discrete points on the Poincare map. The corresponding FFT spectrogram has peaks at the points of mfk/3, but the situation just last for a while, the system turns back to be chaotic.
The state of chaos changes to be stabilized slowly, the system presents obvious 2T-periodic motion when Ωk reaches to 1.104, and its stability is getting better and better as Ωk increases until it comes to 1.186. The chaotic motions appear again in the range of 1.186≤Ωk≤1.37.
For dimensionless frequency 1.372≤Ωk≤1.638, the dynamic solutions are 3T-periodic. What’s more, the system experiences an impressive jump at next moment, and its solution turns to be 2T-periodic at 1.668≤Ωk≤1.696 after a brief struggle against unstable state (1.64≤Ωk≤1.644 and 1.652≤Ωk≤1.666) and 2T-periodic state (1.646≤Ωk≤1.65).
Finally, at high values of the dimensionless frequency, i.e. Ωk≥1.698, the dynamic behaviors keep simple harmonic, with an ellipse in phase diagram, one point in Poincare map and one frequency in FFT spectrogram, as show in Fig. 7(j).
The frequency response amplitude for the system is shown in Fig. 8.
Fig. 8Frequency response amplitude at various mesh frequency for ζ=0.06
In the case ofζ=0.08, it can be seen that the maximum vibration amplitude decreases according to Fig. 6(b). The system performs NHS-periodic motion in the range of Ωk≤0.472. An impressive jump happens at next moment, and the system presents 2T-periodic motion at the same time. Before long, the motion turns back to be NHS-periodic start from Ωk=0.49, with the second jump. As Ωk increases to 0.6, the motion becomes unstable, and bifurcates into 2T-periodic motion at Ωk=0.69 gradually.
As the dimensionless frequency further increases, the system comes into an unstable even chaotic state start from Ωk=0.72, and then goes back to a stable 2T-periodic motion slowly at Ωk=0.94. After a distinct jump at Ωk=1.024 and a chaotic area 1.026≤Ωk≤1.214, the 2T-periodic motion evolves to be 3T-periodic. What’s more, the3T-periodic motion further evolves to be 6T-periodic at Ωk=1.33.
With another jump happens at Ωk=1.39, and in the following range of 1.392≤Ωk≤1.632, the system is mainly under chaotic or unstable state, besides the simple harmonic state happens in 1.542≤Ωk≤1.546 and 1.594≤Ωk≤1.6, and 2T-periodic state happens in 1.616≤Ωk≤1.62. Then, the system exhibits 2T-periodic motion again in the range of 1.634≤Ωk≤1.692. It can be said that the system goes to 2T-periodic motion after the variation between chaos state, simple harmonic state and 2T-periodic state.
After that, the system leads to the area of simple harmonic motion.
The diagram of frequency response amplitude for the system is shown in Fig. 9.
Fig. 9Frequency response amplitude at various mesh frequency for ζ=0.08
In Fig. 6(c), the system also exhibits NHS-periodic motion at low value of dimensionless frequency, i.e. Ωk≤0.176, during this time, the first impressive jump appears at Ωk=0.506. Then, the motion bifurcates to be 2T-periodic in the range of 0.718≤Ωk≤0.764, 4T-periodic in the range of 0.766≤Ωk≤0.858, 2T-periodic in the range of 0.86≤Ωk≤0.882 and 4T-periodic in the range of 0.884≤Ωk≤0.952. The second notable jump happens at Ωk=0.938. After that, the system tends to be unstable even chaotic until Ωk gets 1.134. A 3T-periodic motion appears in the range of 1.134≤Ωk≤1.22. Subsequently, the dynamic solution goes to be chaotic again as Ωk rise from 1.222 to 1.472.
Fig. 10Frequency response amplitude at various mesh frequency for ζ=0.1
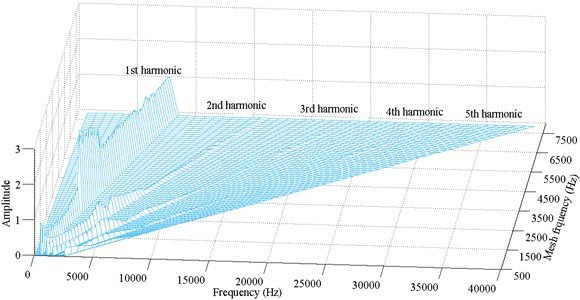
As the dimensionless frequency further increases, the system exhibits simple harmonic motion before the unstable motion presents again at Ωk=1.488. Then a 2T-periodic motion replaces the unstable motion at 1.582≤Ωk≤1.648. Finally, for the dimensionless frequency 1.65≤Ωk≤3, the system performs simple harmonic motion.
Fig. 6(d) reveals the bifurcation characteristics for ζ=0.12 using dimensionless frequency Ωk as bifurcating parameter. Compared with the cases before, bifurcation characteristics here are much simpler. The system exhibits NHS-periodic motion in the range of Ωk≤0.748, and then bifurcates to be 2T-periodic in the range of 0.75≤Ωk≤0.906. The motion further bifurcates to be 4T-periodic as Ωk increases to 0.908, and turn back to be 2T-periodic momently at 0.918≤Ωk≤0.93. Subsequently, the system goes to chaotic area start from Ωk=0.99 after a 4T-periodic motion in the range of 0.932≤Ωk≤0.988.
Fig. 11Frequency response amplitude at various mesh frequency for ζ=0.12
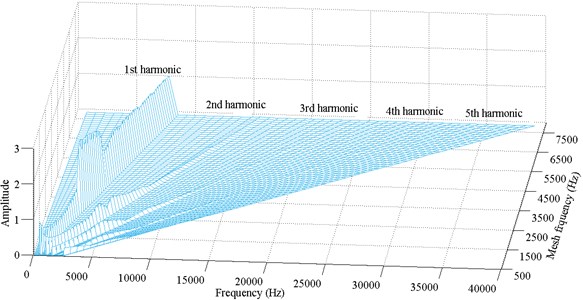
The chaotic motion lasts for a long while until the simple harmonic motion replaces it at Ωk=1.514. In the range of 1.54≤Ωk≤1.6, the motion shifts back and forth between 2T-periodic (sometime stable and sometime unstable) and simple harmonic. Finally, the response keeps simple harmonic at high values of Ωk, i.e. Ωk≥1.602.
The bifurcation behaviors for the case of ζ=0.04 and ζ=0.14 are also investigated using the same method. The plots are not provided here in order to be brief. According to the bifurcation diagrams for different values of the dimensionless frequency, we can find that, impressive jump happens less time as damping coefficient increases.
The unstable and chaotic intervals are much affected as well. According to the discussion above, we can find that the intervals lead to unstable or chaotic responses have a trend to concentration as damping coefficient increases, as shown in Fig. 12.
Fig. 12Intervals of dimensionless frequency lead to unstable or chaotic solution
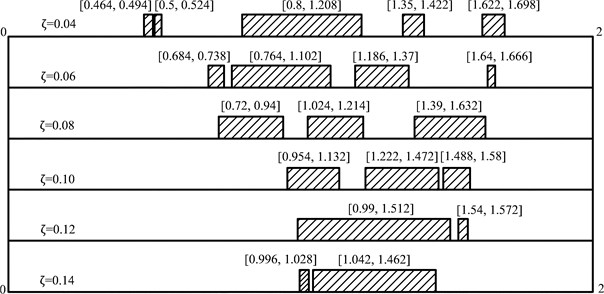
Moreover, the system is more sensitive to the dimensionless frequency at low value of damping coefficient, i.e., the type of motion changes more frequent as dimensionless frequency increases.
The rotational speed that probably causes an unstable or chaotic should be avoided to ensure stability and reliability of the system according to bifurcation diagrams.
3.2. Influence of external excitation
The fluctuation of torque is an important component of external excitation. To research the influence of fluctuation of torque on the bifurcation characteristics, both the fluctuation amplitude and the fluctuation frequency need significant consideration. Here, the system parameters are given as: ˉFm=0.05, ξ=0.25,¯er=0, Ωk=0.2, b=20 μm.
Fig. 13 shows the bifurcation process of the system when ˉFp1=0.02, Ωp=ρpΩk, here ρp is used as control parameter.
Fig. 13Bifurcation diagram using ρp as bifurcation parameter, here ρp=Ωp/Ωk
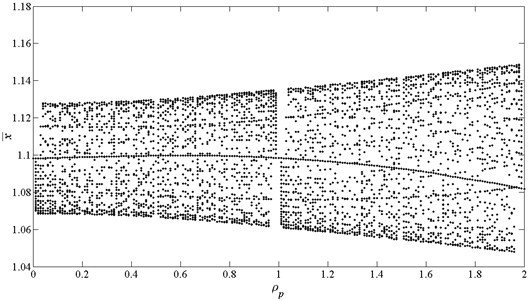
According to Fig. 15, the system presents an interesting bifurcation process. Two excitation sources result in a quasi-periodic motion with the response frequency fr=ifk+jfp, here fk=Ωk/2π, fp=Ωp/2π, i, j= 0, ±1, ±2,…. So, some special values of ρ will lead to special motions
For example, in the case of ρp=0, 1, 2, the system exhibits NHS-periodic motion. In the case of ρp=0.5, 1.5, the system performs 2T-periodic motion. In the case of ρp= 0.25, 0.75, 1.25, 1.75, the virbation response is 4T-periodic. In the case of ρp=0.2, 0.4, 0.6, 0.8, 1.2, 1.4, 1.6, 1.8, the system presents 5T-periodic motion. The corresponding frequency response amplitude diagram reveals the same situation, as shown in Fig. 14.
Fig. 14Frequency response amplitude at various external excitation frequency Ωp
Compared with the effect of external excitation frequency, the effect of external excitation amplitude is much simpler. The bifurcation diagram presented in Fig. 15 reveals that, at low values of ˉFp1, the system performs NHS- periodic motion. As ˉFp1 increases, the motion turns to be 4T-periodic due to the effect of external excitation frequency. What’s more, as ˉFp1 further increases, the motion keep 4T- periodic, the response amplitude is greatly affected.
The corresponding amplitude-frequency characteristic diagram presents the same situation, as shown in Fig. 16.
Fig. 15Bifurcation diagram using F-p1 as bifurcation parameter
Fig. 16Frequency response amplitude at various external excitation amplitude F-p1
It can be found that, the response frequency is composed of non-dimensional frequency fk and external excitation frequency fp; as ˉFp1 increases, the 4T-periodic motion is performed more obvious, and the amplitudes increase.
3.3. Influence of internal excitation
To investigate the influence of internal excitation on the bifurcation characteristics, the system parameters are assigned as follow: ˉFm=0.05, ˉFpr=0,ξ=0.25, Ωk=0.2, Ωe=ρeΩk, φer= –0.72, b=20 μm. Here, both the influences of Ωe and ¯er on bifucation characteristics are also investigated.
Fig. 17 shows the bifurcation characteristics of dimensionless dynamic transmission error by using ρe as control parameter.
Similar to the bifurcation process using ρp as bifurcation parameter, the response frequency of ¯x also composed of the frequencies of two excitation sources, i.e. fr=ifk+jfe. Here fk=Ωk/2π, fe=Ωe/2π, i, j= 0, ±1, ±2,…. Similarly, special values of ρe will lead to specail motions. In the case of, ρe=1, 2, 3, the system performs NHS-periodic motion. In the case of ρe=1.25, 1.75, 2.25, 2.75, the system exhibits 4-periodic motion. In the case of ρe=1.5, 2.5, the system presents 2T-periodic motion.
The difference is that, the response amplitude ¯x has an obviously increase as ρe increases, and when ρe increases to 2.68, the system turns to be unstable. The corresponding amplitude-frequency characteristic diagram is shown in Fig. 18.
Fig. 17Bifurcation diagrams using ρe as bifurcation parameter, here e¯1=0.15
Fig. 18Frequency response amplitude at various internal excitation frequency Ωe
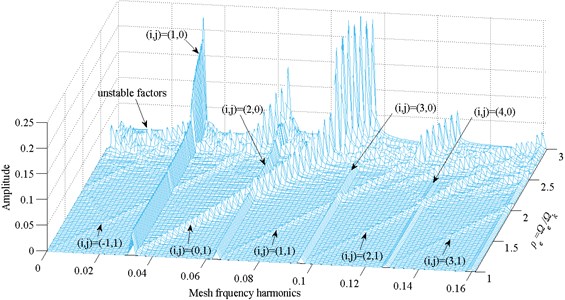
According to figure, it is clear that the response amplitude has a large jumping as ρe increases, and the frequencies resulting in unstable motions are obviously increasing.
Fig. 19Bifurcation diagrams using e¯1 as bifurcation parameter, here Ωk=0.65
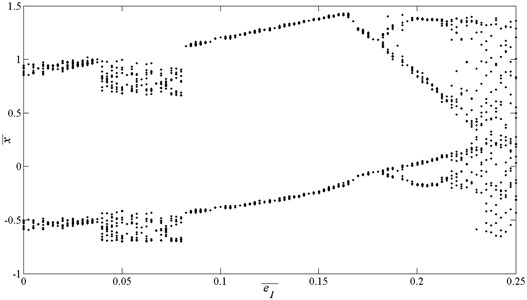
The bifurcation characteristics using ¯e1 as control parameter is clearly presented based on Fig. 20. At the low values of ¯e1, the system exhibits 2T-periodic motion. As ¯e1 increases to 0.04, the motion becomes to be unstable. As ¯e1 further increases to about 0.185, the motion bifurcates to be 4T-periodic. When ¯e1 increases to 0.23, the system presents chaotic motion. According to the corresponding amplitude-frequency characteristic diagram, the unstable and chaotic phenomenon can be easily found. Another conclusion can be got, the growth of ¯e1 has little influence on response amplitude, but has a great influence on the stability of the motion.
Fig. 20Frequency response amplitude at various internal excitation frequency e¯1
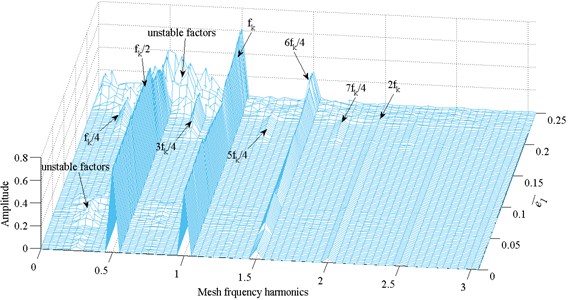
It can also be found that, the response frequency is composed of non-dimensional frequency fk and internal excitation frequency fe; as ¯e1 increases, the system bifurcates from 2T-periodic motion to 4T-periodic motion. The system performs chaotic motion as ρe increases to 2.68 or as ¯e1 increases to 0.23.
4. Conclusions
The micro-segment gear is a new type of gearing and this paper presents a numerical analysis of its bifurcation characteristics. The main conclusions are:
1) The dynamic system is very sensitive to damping coefficient. As damping coefficient increases, the number of bifurcation and impressive jump tend to decrease. In the meantime, the intervals of dimensionless frequency leading to unstable or chaotic motion have a trend to concentration as damping coefficient increases.
2) The motion state of the system often bifurcates though period doubling bifurcation as the dimensionless frequency increases.
3) The influence of external excitation and internal excitation on system’s bifurcation characteristics have similarities and differences. Due to two excitation sources, the responses frequency is composed of non-dimensional frequency fk and external or internal excitation frequency fp/fe.
4) The effects of internal excitation on bifurcation characteristics are greater than that of external excitation. As ρe increases to 2.68 or ¯e1 increases to 0.23, the system exhibits chaotic motion. The growth of ¯e1 affects both the response frequency and response amplitude, while the growth of ˉFp1 only affects the response amplitude.
References
-
Komori T., Ariga Y., Nagata S. A new gears profile having zero relative curvature at many contact points (Logix Tooth Profile). Journal of Mechanical Design, Vol. 112, Issue 3, 1990, p. 430-436.
-
Komori T., Nagata S. A new gear profile of relative curvature being zero at contact points. Proceeding of International Conference on Gearing, China, Vol. 1100, 1988, p. 230-236.
-
Komori T., Ariga R., Nagata S. A new gear profile having zero relative curvature at many contact points (Logix tooth profile). Proceedings of International Power Transmission and Gearing Conference, ASME, Chicago, Vol. 2, 1989, p. 599-606.
-
Han Z., Jinhua L., Hongyu L., Anshi C. Constructing principle and features of tooth profiles with micro-segment. Chinese Journal of Mechanical Engineering, Vol. 33, 1997, p. 7-11.
-
Kang Huang Theoretical and Experimental Research of Micro-Segment Gear. Hefei University of Technology, Hefei, 2002.
-
Huang K., Zhao H., Tian J. Experimental research on temperature rise comparison between micro-segment gear and involute gear. Zhongguo Jixie Gongcheng (China Mechanical Engineering), Vol. 17, Issue 18, 2006, p. 1880-1883.
-
Chen Q., Zhao H., Huang K. Study on calculation of transmission efficiency about the microsegment gear. Zhongguo Jixie Gongcheng (China Mechanical Engineering), Vol. 22, Issue 13, 2011, p. 1537-1539.
-
Kahraman A., Singh R. Non-linear dynamics of a spur gear pair. Journal of Sound and Vibration, Vol. 142, Issue 1, 1990, p. 49-75.
-
Raghothama A., Narayanan S. Bifurcation and chaos in geared rotor bearing system by incremental harmonic balance method. Journal of Sound and Vibration, Vol. 226, Issue 3, 1999, p. 469-492.
-
Parker R. G., Vijayakar S. M., Imajo T. Non-linear dynamic response of a spur gear pair: modelling and experimental comparisons. Journal of Sound and Vibration, Vol. 237, Issue 3, 2000, p. 435-455.
-
Theodossiades S., Natsiavas S. Non-linear dynamics of gear-pair systems with periodic stiffness and backlash. Journal of Sound and Vibration, Vol. 229, Issue 2, 2000, p. 287-310.
-
Moradi H., Salarieh H. Analysis of nonlinear oscillations in spur gear pairs with approximated modelling of backlash nonlinearity. Mechanism and Machine Theory, Vol. 51, 2012, p. 14-31.
-
Vaishya M., Singh R. Analysis of periodically varying gear mesh systems with Coulomb friction using Floquet theory. Journal of Sound and Vibration, Vol. 243, Issue 3, 2001, p. 525-545.
-
Theodossiades S., Natsiavas S. Periodic and chaotic dynamics of motor-driven gear-pair systems with backlash. Chaos, Solitons and Fractals, Vol. 12, Issue 13, 2001, p. 2427-2440.
-
Al-Shyyab A., Kahraman A. Non-linear dynamic analysis of a multi-mesh gear train using multi-term harmonic balance method: sub-harmonic motions. Journal of Sound and Vibration, Vol. 279, Issue 1, 2005, p. 417-451.
-
Tamminana V. K., Kahraman A., Vijayakar S. A study of the relationship between the dynamic factors and the dynamic transmission error of spur gear pairs. Journal of Mechanical Design, Vol. 129, Issue 1, 2007, p. 75-84.
-
Osman T., Velex P. A model for the simulation of the interactions between dynamic tooth loads and contact fatigue in spur gears. Tribology International, Vol. 46, Issue 1, 2012, p. 84-96.
-
Li S., Wu Q., Zhang Z. Bifurcation and chaos analysis of multistage planetary gear train. Nonlinear Dynamics, Vol. 75, Issues 1-2, 2014, p. 217-233.
-
Farshidianfar A., Saghafi A. Global bifurcation and chaos analysis in nonlinear vibration of spur gear systems. Nonlinear Dynamics, Vol. 75, Issue 4, 2014, p. 783-806.
-
Li Z., Peng Z. Nonlinear dynamic response of a multi-degree of freedom gear system dynamic model coupled with tooth surface characters: a case study on coal cutters. Nonlinear Dynamics, Vol. 84, Issue 1, 2016, p. 271-286.
-
Mohammed O. D., Rantatalo M. Dynamic response and time-frequency analysis for gear tooth crack detection. Mechanical Systems and Signal Processing, Vol. 66, 2016, p. 612-624.
-
Velex P., Chapron M., Fakhfakh H., et al. On transmission errors and profile modifications minimising dynamic tooth loads in multi-mesh gears. Journal of Sound and Vibration, Vol. 379, 2016, p. 28-52.
-
Blagojević M., Nikolić V., Marjanović N., et al. Analysis of cycloid drive dynamic behavior. Scientific Technical Review, Vol. 59, Issue 1, 2009, p. 52-56.
-
Zeyin H., Tengjiao L., Chen C., et al. Mathematical models and dynamic contact analysis of involute/noninvolute beveloid gears. Journal of Vibroengineering, Vol. 16, Issue 6, 2014, p. 2949-2961.
-
Xiong Yangshou, Huang Kang, et al. Dynamic modelling and analysis of the microsegment gear. Shock and Vibration, Vol. 2016, 2015.
-
Li T., Zhu R., Bao H., et al. Stability of motion state and bifurcation properties of planetary gear train. Journal of Central South University, Vol. 19, 2012, p. 1543-1547.
Cited by
About this article
This work is supported by the International S&T Cooperation Program of China (2014DFA80440) and the Natural Science Foundation of Anhui Province of China (No. 1408085MKL12).

