Constructed solutions of face gear dynamics associated with engagement impact energy decay

1. Introduction

Face gear drives are addressed by scholars, due to several strengths versus spiral bevel gear drives [1-15], and according to research achievements of Litvin et. al. [16-21], face gear drives are suggested to be used in first-stage gear drives of helicopter main gear boxes. Due to operating characteristics of first-stage gear drives, namely, input-stage gear drives in helicopter main gear boxes, face gear dynamics is focused by many researchers [22-27]. However, according to the limited published issues about face gear dynamics, calculation solutions of face gear dynamics associated with engagement impact energy decay are not to be constructed. Thus, in the study, an engagement impact energy decay calculation solution of face gear drives is proposed, and a four degree-of-freedom (DOF) face gear dynamic model is formulated. Furthermore, the dynamic mesh forces of an example case of face gear drives without considering engagement impacts, as well as with considering engagement impacts and engagement impact suppressions are simulated. The results indicate the fidelity of the proposed calculation solutions of face gear dynamics associated with engagement impact energy decay could be accepted. These contributions would benefit to construct face gear drive modification solutions, and improve engineering applications of face gear drives in the future.

2. Solutions of face gear dynamics associated with engagement impact energy decay

2.2. Four DOF dynamic model

A four DOF dynamic model of face gear drives, as shown in Fig. 1, is formulated for assessing the fidelity of the proposed calculation solutions of face gear dynamics associated with engagement impact energy decay.

Fig. 1A four-DOF dynamic model

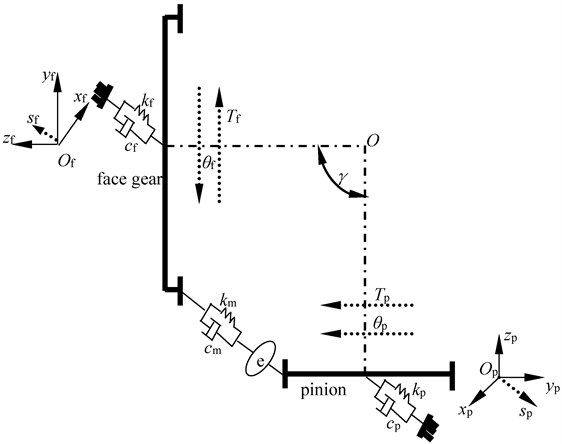
As illustrated in Fig. 1, mathematic equations of the dynamic model can be deduced as:

2

$\left\{\begin{array}{l}{m}_p{s}_p^{\text{'}\text{'}}+c_p{s}_p^{\text{'}}+k_p{s}_p=-F_m,\\ m_f{s}_f^{\text{'}\text{'}}+c_f{s}_f^{\text{'}}+k_f{s}_f=F_m,\\ I_p{\theta }_p^{\text{'}\text{'}}+F_m{R}_{bp}=T_p,\\ I_f{\theta }_f^{\text{'}\text{'}}+F_m{R}_{bf}=-T_f,\end{array}\right.$

where $F_m$ can be written in:

3

$F_m=k_m\mathrm{s}\mathrm{i}\mathrm{n}\left(\gamma \right)\left(s_p-s_f+R_{bp}{\theta }_p-R_{bf}{\theta }_f-e\right)$
$+c_m\mathrm{s}\mathrm{i}\mathrm{n}\left(\gamma \right)\left(s_p^{\text{'}}-s_f^{\text{'}}+R_{bp}{\theta }_p^{\text{'}}-R_{bf}{\theta }_f^{\text{'}}-e^{\text{'}}\right),$

where $\theta$ is a torsion degree of freedom, $s$ is a bending degree of freedom, $T$ is a torsion, $k$ is a bending stiffness, $c$ is a bending damping, $m$ is a quality, $I$ is a moment of inertia, ($\text{'}$) is first derivative, ($\text{'}\text{'}$) is second derivative, subscript $f$ and $p$ express a face gear and a pinion respectively. In addition, $k_m$ is mesh stiffness, $c_m$ is mesh damping, and $e$ is a comprehensive meshing error.

3. Simulations

In order to investigate dynamic mesh force differences of face gear drives among three conditions, namely, without engagement impacts, with engagement impacts, and with engagement impacts associated with impact energy decay, as well as evaluate the fidelity of the proposed calculation solutions of face gear dynamics associated with engagement impact energy decay, geometric parameters, operating conditions and material characteristics of an example case of face gear drives are given in Table 1.

Based on the parameters, listed in Table 1, the STE, which can be calculated according to the reference [28], of the example case among three conditions, meaning, without engagement impacts, with engagement impacts, and with engagement impacts associated with impact energy decay, are simulated, as shown in Fig. 2.

Fig. 3A dynamic mesh force simulation of the example case

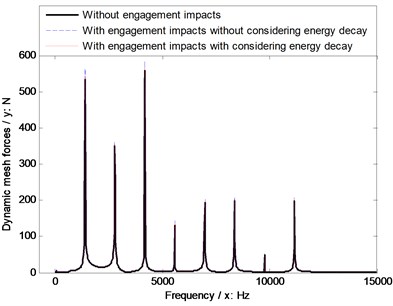
Fig. 2A simulation of STE of the example case

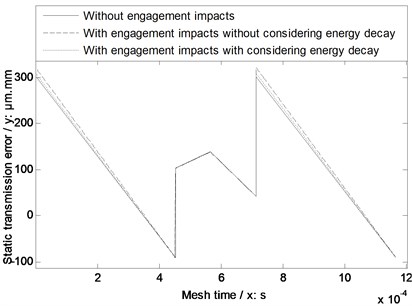
Introducing the results of Fig. 2 into Eq. (2), the dynamic mesh forces of the example case of face gear drives among three conditions are simulated, as shown in Fig. 3.

As illustrated in Fig. 2 and Fig. 3, the STE and dynamic mesh force simulation results with considering engagement impacts associated with energy decay are between the simulation results without engagement impacts and those with engagement impacts, in which energy decay is not considered, which is consistent with the general knowledge and phenomenon of face gear dynamics. Thus, the fidelity of the proposed calculation solutions of face gear dynamics associated with engagement impact energy decay could be accepted.

4. Conclusions

In this study, the most important work is to construct calculation solutions of face gear dynamics associated with engagement impact energy decay. Secondly, the fidelity of the proposed calculation solutions could be accepted according to the simulation results of an example case of face gear drives, which is fit for general cognitions of gear dynamics. These contributions would benefit to improve face gear drive modifications and engineering applications of face gear drives in the future.