Free vibration analysis of doubly convex/concave functionally graded sandwich beams

1. Introduction

Functionally graded materials (FGMs) are non-homogeneous but isotropic material which properties vary gradually and continuously with location within the material. FGMs are developed for military, automotive, biomedical application, semi-conductor industry and general structural element in high thermal environments. Many weaknesses of composites can be improved by functionally grading the material to have a smooth spatial variation of material composition, with ceramic-rich material placed at the high-temperature locations and metal-rich material in regions where mechanical properties need to be high.

Natural vibration frequencies of plates are important in the design and analysis of engineering structures in diverse fields as aerospace, ocean and nuclear engineering, electronics, and oil refineries. Loy et al. [1] have studied the vibration of stainless steel and nickel graded cylindrical shells under simply supported ends by using Love’s theory and Ray-Ritz method. Pradhan et al. [2] have presented the vibration of a FG cylindrical shell. The effects of boundary condition and volume fractions on the natural frequencies are studied. Reddy and Cheng [3] have studied the harmonic vibration problem of FG plates by means of a three-dimensional asymptotic theory formulated in terms of transfer matrix. Vel and Batra [4] have studied the three-dimensional exact solution for the vibration of FG rectangular plates. Based on the higher-order shear deformation theory, Chen [5] has analyzed the nonlinear vibration of a shear deformable FG plate including the effects of transverse shear deformable and rotary inertia. Giunta et al. [6] have presented the free vibration analysis of FG beams via several axiomatic refined theories.

Sandwich constructions have been developed and utilized for almost many years because of its outstanding bending rigidity, low specific weight, superior isolating qualities, good fatigue properties, and excellent natural vibration frequencies. The last characteristic is the major reason why sandwich structures are used more often in aerospace vehicles. Chan and Cheung [7] have carried out a dynamic analysis of multilayered sandwich plates using linear elastic theory. Reddy and Kuppusamy [8] have studied the free vibration of laminated and sandwich rectangular plates using 3-D elasticity equations and the associated finite element model. Kanetmatsu et al. [9], Wang [10] and Lee and Fan [11] have proposed the study of the bending and vibration of sandwich plates. The free vibration analysis of fiber reinforced plastic composite sandwich plates have been presented by Meunier and Shenoi [12]. Pandya and Kant [13] have developed a simple finite element formulation for flexural analysis of multilayer symmetric sandwich plates. A study on the eigenfrequencies of sandwich plates has been presented by Kant and Swaminathan [14].

Recently, sandwich construction becomes even more attractive due to the introduction of advanced composite and FGMs. Sandwich structures made from FGMs have increasing use because of smooth variation of material properties along some preferred direction. Zenkour [15] has studied the buckling and free vibration of FG sandwich plates. Studies on vibration of doubly convex/concave sandwich beams made of FGMs have not been seen in the literature. Compared with FG plates and shells, studies for FG beams are relatively less (Sankar [16], Wu et al. [17], Aydogdu and Taskin [18]). Bhangale and Ganesan [19] have presented the buckling and vibration behavior of a FG sandwich beam having constrained viscoelastic layer in thermal environment by using finite element formulation.

In the present article, free vibration analysis of a variable-thickness FG sandwich beam is presented. The governing differential equation is exactly satisfied at every point of the beam. The boundary conditions at the end edges of the beam are also exactly satisfied. The core layer of the beam is made from an isotropic ceramic material. The bottom face is made of a FG metal-ceramic material, which components vary smoothly in the thickness direction from metal to ceramic ones. The top face is made of a FG ceramic-metal material, which constituents vary smoothly in the thickness direction from ceramic to metal ones. The effective material properties of the present FG sandwich beam are determined using a simple power law distribution. Natural frequencies are presented for metal/ceramic/metal FG sandwich beam with variable thickness. Results obtained are tabulated for future comparison with other investigators. Additional results are plotted to show the effects of vibrations in the geometric and lamination parameters.

2. Geometrical preliminaries

The present study considers FGMs composed of metal and ceramic. The grading is accounted for only across the thickness of the sandwich beam. The present approach adopts the smooth and continuous variation of the volume fraction of either ceramic or metal based on the power law index. The bottom face of the present sandwich beam is made from a metal-ceramic FG material, the core layer is still homogeneous and made from a ceramic material, and the top face is made from a ceramic-metal FG material (see Zenkour [15, 20-24]). The present beam is assumed to have length $L$, width $b$ and variable thickness $h$, as shown in Figs. 1 and 2. Rectangular Cartesian coordinates $\left(x,y,z\right)$ are used and the mid-plane is defined by $z=\text{0}$ and its bounding planes are defined by $z=\pm 1/2h\left(x\right)$.

Fig. 1Plot of the FG sandwich beam with a doubly convex thickness variation (-0.5≤λ≤0)

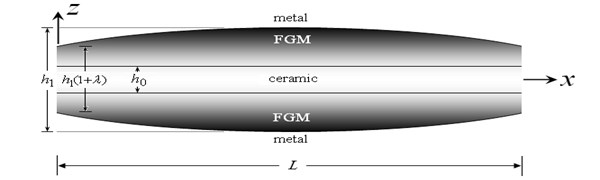
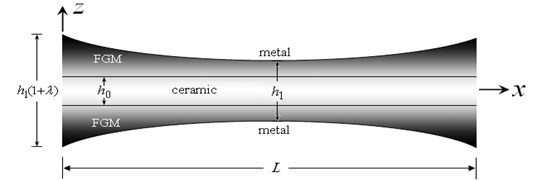
Fig. 2Plot of the FG sandwich beam with a doubly concave thickness variation (0≤λ≤0.5)

A simple power law-type definition for the volume fraction of the metal across the thickness direction of the sandwich beam is assumed. This is defined as:

where $h_0$ is the thickness of the core layer and the volume fraction index $k$ represents the material variation profile through the faces thickness, which is always greater than or equal to zero. The value of $k$ equal to zero represents a fully ceramic beam while the value of $k$ tends to infinity represents fully metal faces with a ceramic core. Based on the volume fraction definition, the effective material property definition follows:

Note that $P\left(x,z\right)$ represents the effective material property for each interval while $P_m$ and $P_c$ represent, respectively, the corresponding properties of the metal and ceramic of the FG sandwich beam. The superscript ‘($n$)’ stands for the layer number ($n=\text{1}$ means bottom face, $n=\text{2}$ means core, and $n=\text{3}$ means top face). Generally, this study assumes that Young’s modulus $E$ and material density $\rho$ of the FGM change continuously through the thickness direction of the beam and obey the gradation relation given in Eq. (2). It should be noted that the material properties of the considered beam are metal-rich at the bottom and top surfaces ($z=\pm h_0/2$) of the beam and ceramic-rich at the interfaces ($z=\mp h_0/2$).

The total thickness of the beam accounts for doubly convexity/concavity variation in the $x$ direction. It reads:

where $h_1$ is the constant reference thickness value located at the beam center ${\text{(}h}_1>h_0\text{)}$, $\lambda$ is a small thickness parameter show the convexity and the concavity of the thickness variation, and $f\left(x\right)$ describes the convex/concave thickness variation of the sandwich beam:

The present sandwich beam has a doubly convex thickness variation when $-\text{0.5}<\lambda <\text{0}$ (see Fig. 1), and it is a doubly concave thickness variation when $\text{0}<\lambda <\text{0.5}$ (see Fig. 2). It is to be noted here that the ends of the beam is $\text{(}1+\lambda \text{)}$ times thicker (thinner) than the thickness at the center of the beam, $x=L/2$.

3. Basic equations

The dynamic version of the principle of minimum of the total energy is used to derive the governing equation and associated boundary conditions. It is given in terms of the deflection $w$ and the transverse distributed load $q$ is as:

where:

in which $E\left(x,z\right)$ and $\rho \left(x,z\right)$ are given according to Eq. (2). The associated boundary conditions are given as follows:

1) $w$ is specified or $I_2\left(x\right)\frac{d\ddot{w}}{dx}+\frac{d}{dx}\left(I_e\left(x\right)\frac{d^{2}w}{d{x}^2}\right)=0$.

2) $\frac{dw}{dx}$ is specified or $\left(I_e\left(x\right)\frac{d^{2}w}{d{x}^2}\right)=0$.

The moment and shear force are given by:

4. Free vibration of sandwich beams

The edges of the considered beam $\text{(}x=0,L\text{)}$ have two combinations of simply supported (S) and clamped (C) boundary conditions. The displacement $w$ is presented as products of determined function of the axial coordinate and unknown function of time. For free vibration, the load force $q$ is vanished and the displacement is given by:

where ${\omega }_m$ denotes the eigenfrequency associated with the $m$ eigenmode, $W_m$ is arbitrary parameter and $\xi (\equiv x/L)$ is the dimensionless axial variable. The function $X\left(\xi \right)$ depends on the boundary conditions on the beam edges as follows:

SS:

CS:

Using Eq. (8) into the governing equation, Eq. (5), and setting $q=0$, one obtains:

where:

and

is the frequency parameter of the natural vibration. After imposing the boundary conditions of the problem, Eq. (11) can be solved directly by numerical computation to obtain the positive root of the frequency parameter $\mathrm{\Omega }$ according to the SS and CS boundary conditions.

5. Numerical examples and discussion

The FGM can be obtained combining two distinct materials such as a metal and a ceramic. The isotropic FG sandwich beam considered in the examples is assumed to be composed of metal (Ti-6Al-4V) and ceramic (zirconia-ZrO₂). The relevant material properties for the constituent materials are listed in Table 1 (Reddy and Chin [25]).

The dimensionless fundamental frequencies $\text{(}m=\text{1)}$ for a doubly convex FG sandwich beam with $h_1/h_0=\text{2}$ and $L/h_0=\text{10}$ at the center of sandwich beam are presented in Table 2 for different values of the volume fraction index $k$ and the thickness parameter $\lambda$. Similar results for the doubly concave sandwich beam are presented in Table 3. It is to be noted that, frequencies increase as $k$ increases and $\lambda$ decreases and this irrespective of the boundary conditions. As the volume fraction index $k$ tends to infinity (full ceramic beam), the frequencies are the same for the two shapes of the beam and are independent on the thickness parameter $\lambda$.

The dimensionless natural frequencies for a doubly convex $\text{(}\lambda =-\text{0.5)}$ and a doubly concave $\text{(}\lambda =\text{0.5)}$ FG sandwich beams with $h_1/h_0=\text{2}$, $L/h_0=\text{10}$ and $h_1/h_0=\text{2}$ and $\xi =\text{0.5}$ are given, respectively, in Tables 4 and 5. Once again, the frequencies increase as $k$ increases and the eigenmode $m$ increases. Some plots are presented for natural frequencies $\text{(}m=\text{5)}$ of FG sandwich beam $\text{(}k=\text{5.5)}$ with doubly convex/concave thickness variations $\text{(}\left|\lambda \right|=\text{1/3)}$. All plots shown henceforth are obtained for natural frequencies versus the thickness ratio $h_1/h_0$ at $L/h_0=\text{10, 15, 20}$ and 25. Figs. 3 and 4 show that the frequencies for beams subjected to SS and CS boundary conditions are stable and increasing with the increase of $h_1/h_0$ and $L/h_0$ ratios.

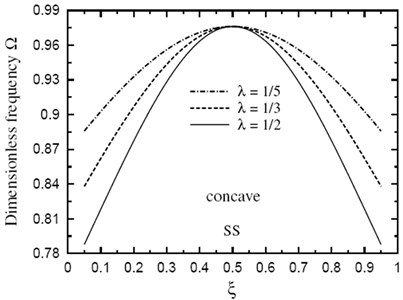
Finally, the dimensionless fundamental frequency is plotted through the length of the FG sandwich beam according to different parameters. Figs. 5 and 6 show plots of the fundamental frequency of a SS doubly convex/concave FG sandwich beam with the volume fraction index $k=\text{5}$, $h_1/h_0=\text{3}$, $L/h_0=\text{10}$ and for different values of $\lambda$. However, Figs. 7 and 8 show plots of the fundamental frequency of a SS doubly convex $\text{(}\lambda =-\text{0.5)}$ or concave $\text{(}\lambda =\text{0.5)}$ FG sandwich beam with the volume fraction index $k=\text{3.5}$, $h_1/h_0=\text{3}$ and for different values of $L/h_0$ ratio. In addition, Figs. 9 and 10 shows fundamental frequencies of doubly convex/concave SS sandwich beam with fully metallic faces and ceramic core ($k$ tends to infinity).

As shown in Figs. 5-10, results are symmetric about the center of the beam. Frequencies are maximum at the edges of the doubly convex beam and at the center of the doubly concave beam. Once again, frequencies increase as $\lambda$ decreases. However, the value of $\lambda$ has a very little effect on frequencies at the center of beam with fully metallic faces and ceramic core.

Fig. 3Natural frequency Ω vs thickness ratio h1/h0 for a SS FG sandwich beam with doubly convex/concave thickness variation

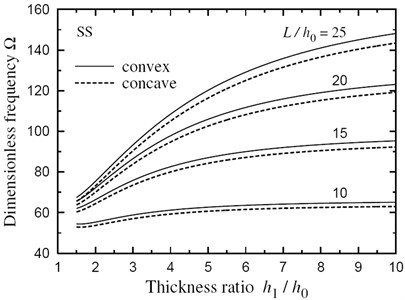
Fig. 4Natural frequency Ω vs thickness ratio h1/h0 for a CS FG sandwich beam with doubly convex/concave thickness variation

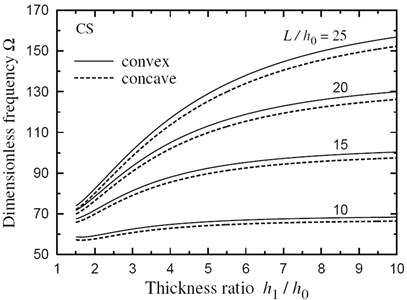
Fig. 5Fundamental frequency Ω through the length of a doubly convex SS FG sandwich beam for different values of ξ(k=5, h1/h0=3, L/h0=10)

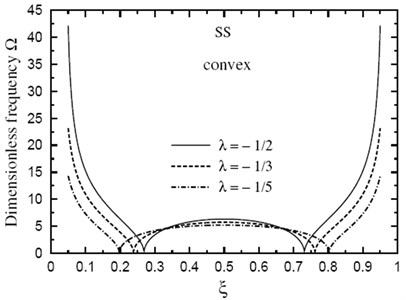
Fig. 6Fundamental frequency Ω through the length of a doubly concave SS FG sandwich beam for different values of ξ(k=5, h1/h0=3, L/h0=10)

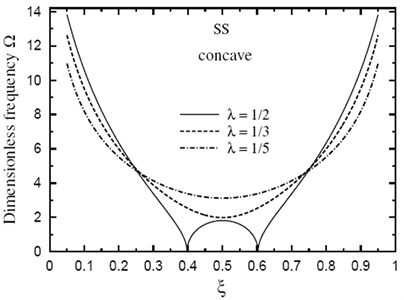
Fig. 7Fundamental frequency Ω through the length of a doubly convex SS FG sandwich beam for different values of L/h0(k=3.5, h1/h0=3)

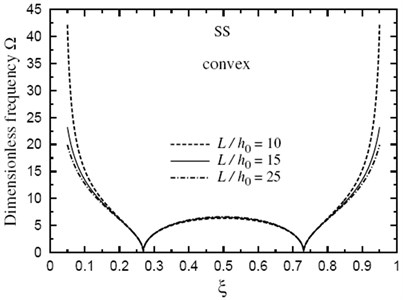
Fig. 8Fundamental frequency Ω through the length of a doubly concave SS FG sandwich beam for different values of L/h0(k=3.5, h1/h0=3)

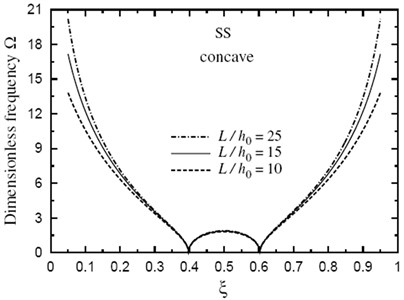
6. Conclusions

This article focuses on the derivation of natural vibration frequencies of variable-thickness FG sandwich beams subjected to various boundary conditions. The core layer is composed of a homogeneous ceramic material while the faces are made of a symmetric FG metal-ceramic material. The material properties such as Young’s modulus and material density can vary through the axial and thickness directions of the beam according to a mixed power-law type distributions. Some vibration frequencies for metal-ceramic/ceramic/ceramic-metal sandwich beam with a doubly convex/concave variable thickness are tabulated for future comparisons. The effects of many parameters such as thickness ratio, length-to-core thickness ratio, thickness parameter and the volume fraction index on frequencies are investigated. The results show that the fundamenta1 frequencies are similar to that observed for homogeneous convex/concave beams and the natural frequencies are affected by the thickness variation and the constituent volume fractions and the configurations of the constituent materials.

Fig. 9Fundamental frequency Ω through the length of a doubly convex SS sandwich beam of fully metallic faces and a ceramic core (k→∞, h1/h0=3, L/h0=10)

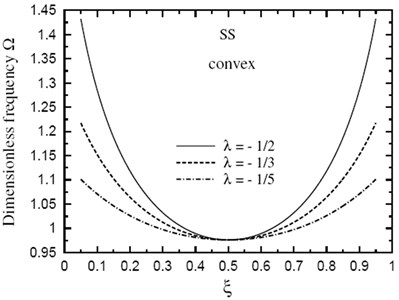
Fig. 10Dimensionless fundamental frequency Ω through the length of a doubly concave SS sandwich beam of fully metallic faces and a ceramic core (k→∞, h1/h0=3, L/h0=10)