Human activity recognition: classifier performance evaluation on multiple datasets

1.1. Current approaches in activity recognition

In general, in activity recognition authors attempt to recognize static states (lying, sitting, standing, etc.), dynamic states (walking, running, etc.) and/or transition states (i.e. standing to walking). Data preprocessing to improve the classification accuracy is common [1-3]. Classification methods currently widely used in the area are based both on classic algorithms like the Classification And Regression Tree (CART) [4, 5] or k-Nearest Neighbor (k-NN) [6, 7] and more advanced techniques like the Adaptive Neuro Fuzzy Interference System (ANFIS) [8, 9] or Iterative Dichotomiser 3 (ID3) [10] and others.

2.1. The opportunity dataset

This dataset has been created to provide a benchmark for HAR methods. It consists of three different sensor systems (wearable, ambient, object-attached) and contains a wide variety of activities described and distinguished by many parameters (sensor data, limb used to perform them, etc.). The dataset provides a total of 242 parameters, 144 of which are data from wearable sensors, that is 7 inertial record units (IMUs), 12 3D acceleration sensors and 4 3D localization sensors, 60 parameters are taken from object sensors placed on 12 objects and 37 parameters correspond to data obtained from ambient sensors (13 switches and 8 3D acceleration sensors). The dataset was collected from 4 subjects in 6 runs, during 5 of which they were performing activities of daily living (ADL) and one run was a “drill” run in which the subjects specifically performed a particular activity.

For the purposes of this paper, only the wearable sensor portion of the dataset was extracted. ADL and drill activities were merged into a single set as their division was not relevant in the task ahead. As some of the parameters were statistics computed from the records, these parameters were not taken into consideration. Overall, 133 parameters per record were used, making this dataset the most elaborate (and the most computationally expensive) of the three. Its detailed descriptions can be found in [11] and [12] with further reading on its application in, for example, [13].

2.2. The PAMAP2 dataset

The PAMAP2 dataset contains data of nine healthy human subjects, each wearing three IMUs by Trivisio, Germany and a heart rate monitor. Each of the three IMUs measures temperature and 3D data from an accelerometer, gyroscope and magnetometer. The data is sampled at 100 Hz and transmitted to PC via a 2.4 GHz wireless network. Subjects wore one IMU on the dominant wrist, one on the dominant ankle and one on the chest. Detailed information on the dataset can be found in [14] and [15].

The methods have been tested on all 9 test subjects in the dataset, labeled in the dataset as subject101 through subject109. Data of all these subjects consists of 2872532 records, each containing 54 values. The description of the values is also included in the dataset documentation. Some values can be missing, indicated with a NaN (Not a Number) value.

Aside from the total of twelve activities performed by the subjects, the dataset also contains transition activities (data collected while not clearly performing any of the desired activities). These were discarded as their relevance is not assured. Since some records contain only NaN values, these were discarded as well. From each record, irrelevant values, that is the orientation of each IMU and timestamp, were removed. Since most heart-rate values were NaNs due to a different operating frequency, they were also removed. As a result, each record contains 36 values.

2.3. The localization dataset

A simple yet very interesting dataset consisting of 4 localization tags placed on the ankles, belt and chest of the user. Originally described and used in [16], this dataset was primarily focused on detecting activities that could help identify emergency situations and provide a basis for remote care systems for elderly people. The dataset could be considered quite minimalistic as each record contains only 8 parameters: sequence ID, tag ID, timestamp, date, 3 localization coordinates for a tag and a class label. Disregarding the sequence IDs, timestamps and dates as irrelevant and separating the class label, the final dataset was the smallest one with only 4 parameters per record.

Unfortunately this dataset did not contain a pure standing activity, which is why this particular activity, while being one of the base activities for any other one, was included in the others class even though the previous two datasets do distinguish it.

3.1. k-Nearest Neighbors

k-NN is a non-parametric algorithm, meaning that it makes no assumptions about the structure or distribution of the underlying data, thus being suitable for real-world problems that usually do not follow the theoretical models exactly. The method is also considered to be a lazy learning algorithm as it performs little to no training during computation. As a result, the method uses the whole training dataset during classification. k-NN is well known for its simplicity, speed and generally good classification results in applications like bioinformatics [26], image processing [27], audio processing [28] and many others.

3.2. Classification and regression tree

This algorithm classifies a sample according to groups of other samples with similar properties. During training, the training data is continuously divided into smaller subsets (tree nodes). When the divisions are finished, the samples are clustered together according to their properties. Testing samples are then evaluated against certain conditions in each node and propagated throughout the tree. When the sample reaches a leaf node, it is then assigned the class to which the samples in that node belong. In this paper, a binary tree with logical conditions was used. CARTs are still under extensive research and can be used as a standalone classifier [29] or as a part of larger algorithmic structures [30].

3.3. Random forest

RF is an ensemble algorithm consisting of a number of CARTs combined together into a single voting system. Each CART receives a dataset with only a subset of parameters, giving it a perspective and knowledge about the problem unique from any other CART. These parameters are chosen randomly, but each parameter set is unique. The number of parameters to choose for each CART as well as the number of CARTs in the forest are the only two variables that are subjects to change when performing experiments, making it easy to use. Its downside is both time and spatial complexity inherent to its nature. However, the algorithm has been shown to be very robust in performance in many research areas [31, 32], making it a suitable alternative for consideration in both classification and regression problems.

3.4. Linear discriminant analysis

LDA is a well-known technique used to identify sample clusters in a given set of data. It attempts to divide clusters (data classes) with a linear function so that the classes are as distant from each other as possible, but at the same time keeping the distance between individual data samples in a single class minimal. The method assumes that the data in each class is normally distributed, but it has still been successfully applied in many problems of automatic recognition, for example in image feature extraction [33] or speech recognition [34].

3.5. Quadratic discriminant analysis

As the name suggests, QDA is very closely related to LDA with the exception that QDA does not assume the normal distribution of the data in each class. Instead of the linear function that separates the classes from each other, the function used by QDA is quadratic and can be considered to be a generalization of LDA. Due to its greater time complexity, the method is not as widely used as LDA, but it is still feasible in many applications, including bioinformatics [35] or molecular physics [36].

3.6. Nearest centroid classifier

An extremely fast classifier. The approach is similar to that of k-NN, but instead of k closest training samples the method picks the label of the class whose training samples' mean (centroid) is the closest to the signal query. The speed and simplicity of the algorithm is compensated by low classification performance. Therefore the classifier is usually coupled with one or more data preprocessing techniques. In many implementations the method has been successfully used to create pattern recognition systems in bioinformatics [37, 38].

4.1. Classification

To classify the query signal vector, a strategy of computing the residual value from the difference between the query vector and its sparse representation converted into the vector space of the training matrix vectors is employed. This is performed for each class resulting in $c$ residuals. The classification is then based on the minimum residual. Formally, the classification problem can be stated as follows:

Here, ${\mathbf{s}}_k$ is an $n$-dimensional vector with non-zero elements located only on the indices corresponding to the $k$th class in the training matrix, hence the need for the training samples of a given class to be grouped together in the matrix. The algorithm could be described by the following steps:

⦁ Set the iteration variable $i$ to 1.

⦁ Replace all sparse coefficients with indices not corresponding to class $i$ with zeros.

⦁ Multiply the training matrix with the modified vector $\mathbf{s}.$

⦁ Compute the ${\mathcal{l}}^2$-norm of the resulting vector.

⦁ Increase $i$ by 1 and repeat for all classes.

⦁ Output the class whose ${\mathcal{l}}^2$-norm is the lowest.

Computing the residuals is generally not computationally expensive and can be performed in real time, depending on the size of the training matrix. Only very large training matrices can slow the process down significantly.

Aside from the modification above, we also used a tensor adaptation that we developed and described in [40]. This adaptation restructures the data into a tensor and implements elements of the ensemble paradigm into its classification procedure. Experiments confirming its ability to generally perform better than the original OMP version in a HAR problem was included in [40].

5.1. Experimental settings

The execution of some of the algorithms can be customized through execution parameters which, for these experiments, were set according to the best empirical speed/accuracy ratio. While the goal was to make the results as comparable as possible despite using datasets with greatly dissimilar properties, the Localization dataset contained so few parameters that the evaluation required a different setting. The common settings in terms of customizable algorithms for all dataset were as follows: as all algorithms were implemented in the latest version of MATLAB, the default MATLAB settings were used for CART. k-NN was experimented upon with four settings of the $k$ parameter: 1, 3, 5 and 10. As k-NN is a classic and very well known classifier, we decided to include these four most successful settings as opposed to just picking one that performed the best. LDA, QDA and NCC were not customizable.

For the OMP classifiers (designated as OMP for the original version, OMPmod for the modification described in section 4 and OMPten for the tensor adapation) and RF, the number of parameters per record in the Localization dataset was limiting. While for the PAMAP2 and Opportunity datasets the methods were set to 10 sparse coefficients (OMPs) and 1000 trees each accepting 6 input parameter each (RF), the Localization dataset, due to it having only 4 parameters per record, had to make do with 2 sparse coefficients and 6 trees calculating 2 parameters each. While this setting does seem quite restrictive, OMP should compute only as many sparse coefficients as there are parameters and RF used the highest setting possible as there are no more than 6 combinations of 4 parameters taken 2 at a time.

Given the difference in the number of records in each dataset, a compromise had to be made in this area as well. The lowest number of records were in the Localization dataset (164850 records), the number of samples taken for one experiment was, therefore, reduced to 150000. As most of the samples in the other two datasets would be discarded, we performed a total of 5 completely random selections of 150000 samples. For each selection, the experiments were conducted and the results averaged, taking much greater data space of the datasets into consideration during the experiments.

The entire dataset was divided into a training and a testing set. Experiments were performed on 5 different settings with the training set being a 10 %, 20 %, 30 %, 40 % or 50 % portion of the selected samples. The rest was used for evaluation. Since not all of the classifiers provide a validation step, the step was omitted from the evaluation process. This could also be considered a kind of a restriction as it is common in data processing to use portions of about 70 % for training. Since the time complexity of the algorithms vary greatly, performance records in speed of computation time were also conducted. The times were calculated as the worst case scenario for the 50 % training set only. Note that if the classifier first created a model from the training set and then used it for classification (like CART and RF), the training part is not included as, in practice, training is usually not a time-critical computation and is done in advance. In cases when the testing phase was too fast to measure on the per-record basis (like all CART evaluations), the whole testing phase was measured and TPM (Time Per Record) was calculated by dividing the resulting time by the number of records in the test phase.

The experiments were run on a computer equipped with a quad-core Intel Core i5-750 2.67 GHz processor, 8 GB of DDR3 RAM effectively clocked at 1333 MHz, Windows 8.1 operating system and the latest version of MATLAB.

5.2. Results

The averaged classification accuracies given as percentual success rates are shown in Tables 2-4 where the classifiers are sorted according to their best results (regardless of the training set size) in the descending order. For all methods except for LDA, QDA and NCC, larger training set resulted in more or less improved accuracy. LDA, QDA and NCC, on the other hand, suggest that in HAR problems, the training set size does not matter to them. This does not come as a surprise as no matter the training set size, data distribution (for LDA and QDA) and the centroid location (for NCC) remain the same. This property can clearly be seen in Figures 1-3 where the accuracy changes very little with the training set size. While the charts can seem rather redundant, the behavior of the classifiers is worth noticing as they all scaled about the same in terms of improving the accuracy with greater training size. Considering the variety of data acquisition devices used in the three datasets and of the classifiers themselves, the charts suggest a hidden property of the HAR problem that is certainly worth investigating. Note that in Figure 3, even though the differences between training set sizes are slightly exaggerated by a different $y$-axis scale, LDA, QDA and NCC still show little to no difference in performance.

Fig. 1Graphical representation of the accuracies achieved for different training sets (10 % through 50 %, left-to-right order) and classifiers. Localization dataset

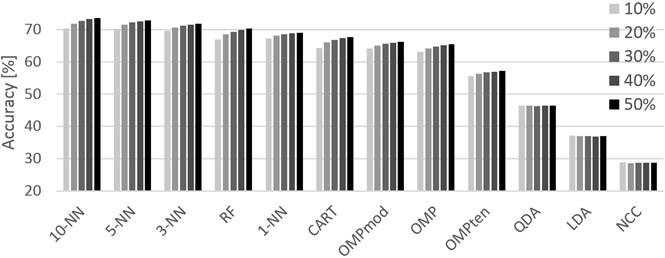
Fig. 2Graphical representation of the accuracies achieved for different training sets (10 % through 50 %, left-to-right order) and classifiers. PAMAP2 dataset

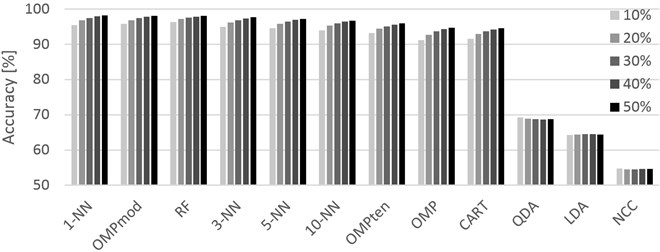
Fig. 3Graphical representation of the accuracies achieved for different training sets (10 % through 50 %, left-to-right order) and classifiers. Opportunity dataset

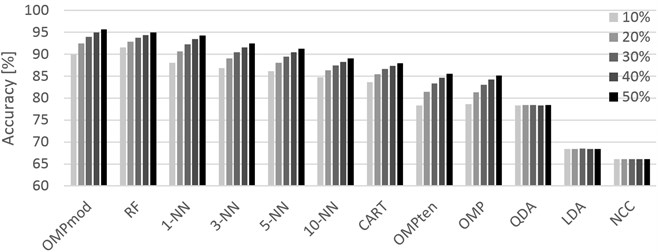
For the Localization dataset (Table 2), the results are generally discouragingly low, topping at 73.55 % for k-NN with $k=\text{10}$. This suggests that while the dataset can provide some accuracy, the data collection setting using only four localization tags is not suitable for the task as specified in this paper. K-NN was, in this case, the best performing algorithm almost regardless of its setting. The differences between individual algorithms are not too great, giving the potential user freedom in choosing a method in terms of calculation speed.

The PAMAP2 dataset (Table 3) has shown promising results before, and the results were confirmed in these experiments as well. With the maximum accuracy at 98.16 % by 1-NN followed very closely with the difference of only 0.04 % by our proposed method, the dataset appears to present a highly reasonable compromise between accuracy and price of the data capturing solution. With the exception of LDA, QDA and NCC, the classifiers performed quite well, offering a variety of methods for solving HAR problems using the capturing settings as defined in the PAMAP2 dataset documentation.

Finally, the Opportunity dataset (Table 4) shows promising and satisfactory results while its setting seems to be the most suitable for our modification of the OMP based classifier. The classifier surpassed all other classifiers with the lead of 0.78 %, 1.45 % and 7.75 % against RF, 1-NN and CART, respectively. Practical usefulness of OMPmod over RF depends on future time complexity reduction as the method is noticeably slower than RF. It is also noteworthy that RF performed better than any other classifier for 10 % and 20 % training set sizes in PAMAP2 as well as Opportunity, however practical application with the provided accuracy results could be doubted given the potential when using more data for training.

The approximate times required to classify one record for each classifier are listed in each table in the TPM column. The values are in milliseconds. As is often the case, the least accurate ones are the fastest. This holds true in these experiments as well when the fastest of the tested algorithms, NCC, performed very poorly. QDA performed significantly better while being only slightly slower, but still could not provide satisfactory accuracy. While RF, k-NN and OMPmod are relatively slow methods in comparison, their speed is still sufficient for practical application providing, at worst, 5 classifications every second for the PAMAP2 dataset. Though the most accurate when dealing with the Opportunity dataset, OMPmod was also the slowest, providing only one to two classifications every second. In this case, practical use might depend on the requirements of the customer, but it is reasonable to assume that humans will not switch activities every second or even more often.