Noise and vibration assessment of permanent-magnet synchronous motors based on matching pursuit

Chen, Zhong; Zhang, Xianmin

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 June 2014

Check for updates

Noise and vibration assessment of permanent-magnet synchronous motors based on matching pursuit

Zhong Chen¹

Xianmin Zhang²

^{1, 2}GuangDong Provincial Key Laboratory of Precision Equipment and Manufacturing Technology South China University of Technology, Guangzhou, P. R. China

^{1, 2}School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou, P. R. China

Corresponding Author:

Zhong Chen

Cite the article Download PDF

Downloads 1277

Abstract

This paper presents a noise and vibration assessment scheme for the elevator permanent-magnet synchronous motors (PMSMs) based on matching pursuit (MP) with carefully selected atoms. The atomic dictionary is developed by considering of the complication of electromagnetic noise and vibration of the elevator PMSMs. After identifying the natural frequencies by modal testing and computing the characteristic electromagnetic frequencies of the PMSMs, the impulse energy ratio based on transient components, which are extracted by projecting on the selected atoms based on the MP method, are computed and used to assess the machines. The assessing results indicate that the transient components can accurately represent the electromagnetic impulse since the distorted magnetic fields and the features are robust for quality inspection of the elevator PMSMs.

1. Introduction

Permanent-magnet synchronous motors (PMSMs) have been adopted by a lot of machines, such as the automobiles, the robots and the elevator traction machines etc., due to their quieter performance than that of switched reluctance and induction motors. In general, noise and vibration of PMSMs are mainly induced by electromagnetic and mechanical exciting force. Electromagnetic noise and vibration of PMSMs mainly come from cogging torque, torque ripple, and magnetic radial forces. Mechanical noise and vibration of PMSMs mainly come from rotating parts, such as bearing. But all of the noise and vibration are primarily radiated and shown through the PMSMs body, in which the intrinsic dynamic characteristics have an important impact. According to references [1-3], noise and vibration of this kind of machines are mainly caused by radial electromagnetic force that is generated by electromechanical interaction in the air gap of a PMSM. Although an optimized PMSM could be designed in consideration of various factors including tooth shape, magnet pole angle, combination of pole and sole numbers, rotor eccentricities, inverter PWM carrier signal, and so on [4-7], the electromagnetic fields of the ultimate machines could still be distorted by the parameters’ variations, such as variations of the permanent-magnetic material parameters, pole location errors in a rotor, and eccentricities between a stator and a rotor in a PMSM. These variations, caused in the manufacturing and assembly process, could result in non-stationary noise and vibration of a PMSM. Therefore, robust features related to these defects should be extracted precisely from vibration signals by using advanced signal analysis methods.

Traditional signal analysis methods such as spectrum, envelope demodulation and cepstrum analysis have been employed for defects detection of motors [8-9]. Various time-frequency analysis methods have been applied in fault feature extraction of electrical machines in order to extract their non-stationary fault features. Cristalli et al. [10] applied the short-time Fourier transform (STFT) method to detect the failure features of a motor bearing in the time-frequency domain. Antonio-Daviu et al. [11-12] used the Hilbert-Huang transform (HHT) to diagnose the mixed eccentricity fault of an induction motor as compared to wavelet transform method, and track the characteristic transient evolution of a particular fault-related component of the failures in damper windings of synchronous motors. Riera-Guasp et al. [13] employed the Gabor time-frequency method to generate high resolution time-frequency stamps of different types of faults, such as the broken bars and mixed eccentricity faults of an induction motor. The above-mentioned methods mainly base on Fourier basis-expansion, and are only successfully applied in the fault diagnosis of a motor in operation.

Matching pursuit (MP) method, which is introduced by Mallat and Zhang [14], is a kind of atomic decomposition methods, which computes the signal approximations from a redundant dictionary by iteratively selecting one vector at a time [15]. With a problems-oriented redundant atomic dictionary, the meaningful components can be projected into the related atomic bases sparsely and efficiently. Many researchers applied this method in the fields of fault diagnosis of bearings [16, 17], gears [18], and breast cancer [19]. It is meaningful that non-stationary vibration signal of the motors is processed by using the MP method in order to implement quality monitoring of PMSMs in its manufacturing process.

In this paper, the vibration signals of the elevator traction machine, which is an external rotor PMSM, are analyzed and subjected to the MP method for noise and vibration assessment, as well as the failure recognition. In Section 2, the suitable atoms are selected and an optimal redundant dictionary is build up according to the energy ratios between the projections and the original signals for the finite samples. The MP-based signal decomposition method and the noise and vibration assessment scheme for the PMSMs are introduced. In Section 3, the intrinsic characteristics of the PMSM's body are obtained by modal testing of the PMSMs, and various elevator PMSMs are assessed according to the assessment scheme. The concluding remarks are given in Section 4.

2. Assessment scheme based on matching pursuit

2.1. Building of a dictionary

Since the characteristics of the non-stationary impulse and the harmonic wave are frequently embedded in the vibration signals of the unqualified PMSMs, atomic functions in MP algorithm should be carefully selected according to the criterion of adaption to the signal features. Atomic functions in MP algorithm mainly include Fourier-based functions, such as the sine function, the cosine function, the discrete cosine transform-II basis (DCT II), time-frequency functions, such as various wavelet function and wavelet packet, and Kronecker delta function [15].

Table 1The energy ratios between the projections and the original vibration signals

Atoms type	No. 1	No. 2	No. 3	No. 4	No. 5	No. 6
Sin	0.489281	0.359808	0.478384	0.347939	0.368390	0.826936
DCT II	0.732533	0.744054	0.738899	0.626174	0.576048	0.970080
Wpsym4-5	0.489736	0.631208	0.375593	0.336352	0.404387	0.513062
Sin+Wpsym4-5	0.646450	0.664261	0.590921	0.439555	0.502171	0.941226
DCT II+Wpsym4-5	0.742739	0.758717	0.744465	0.634790	0.601093	0.974292
Sin+DCT II+Wpsym4-5	0.757809	0.772107	0.771510	0.646449	0.617912	0.981396

In order to detect the harmonic vibration signal of the PMSM, sine function and discrete cosine transform-II basis are selected for the decomposition of vibration signals of the PMSM. In order to detect transient contents of the vibration signals of the PMSM, the Daubechies least-asymmetric wavelet packet with 4 vanishing moments at level 5 is selected, which is briefly named as Wpsym4-5 or Daubechies symlet packet. Since symlet wavelet has a compact support and an almost linear phase, its packet is embedded in the dictionary of the MP algorithm for decomposing non-stationary impulse contents. But the atom type and their combination should be determined optimally in order to decompose the vibration signals efficiently and sparsely. So we design an evaluation experiment in which the energy ratios between the projections and the originals using MP algorithm are computed in 100 iterated steps. The largest energy ratio will indicates the combination of atom types best suitable. The vibration signals of the 6 MPSMs are selected, which include 5 ones in bad condition (No. 1-No. 5) and one in good condition (No. 6). The results are listed in Table 1.

From the above results, the atom combinations of sin, DCT II and Wpsym4-5 could be used to decompose the vibration signals efficiently and sparsely, and should be selected to build the redundant dictionary. After atomic functions have been determined, the dictionary ${\{ϕ_{n}\}}_{n \in Γ}$ is defined, where $Γ$ is $m \times n$ sets, in which $m$ is the index of the above defined atomic types, and $n$ belongs to non-negative integer sets.

2.2. Decomposition algorithm based on matching pursuit

The primary task of the MP algorithm [14] is to decompose vibration signal of the PMSM into a linear combination of the pursued basis functions.

Given that $f (x)$ is the vibration signal of the PMSM and let $R^{0} f (x) = f (x)$ , $ϕ_{0}$ is selected according to the criterion of maximization of the absolute value of inner product $〈f_{0} (x), ϕ_{0}〉$ over the whole dictionary. Then $f (x)$ can be represented as:

1

f (x) = 〈f (x), ϕ_{0}〉 + R^{1} f (x),

where $R^{1} f (x)$ is the residual after the first approximation. The residual $R^{1} f (x)$ can be further decomposed as the above process. The optimal atom $ϕ_{1}$ is selected as the criterion of maximization of $|R^{1} f (x), ϕ_{1}|$ . The procedure repeats until a desired approximation precision or number of iteration is reached. After $K$ th iteration, the signal $f (x)$ can be represented as:

2

f (x) = \sum_{n - 1}^{K - 1} 〈R^{n} f (x), ϕ_{n}〉 + R^{K} f (x) .

Finally, the transient signal contents can be rebuilt by the selected symlet packet atoms. The harmonic signal contents can be rebuilt by the selected discrete cosine basis and sine basis. These decomposed signal contents indicate the important physical meanings of the machine conditions.

2.3. Assessment scheme of noise and vibration of the PMSMs

After the atoms are selected, the assessment scheme based on the MP algorithm can be defined as follows:

Step 1: the projections are computed using the MP algorithm based on the built dictionary. The transient contents and the harmonic contents of signal $f (x)$ is extracted according to the selected symlet packet atoms and the atoms of selected discrete cosine basis and sine basis respectively.

Step 2: the power spectrum density (PSD) method is used to analyze the transient and the harmonic contents. These decomposed signal contents and its PSD indicate the important physical meanings of the machine conditions, and is used to assess noise and vibration of the PMSMs initially.

Step 3: the impulse energy ratios are computed, which are used to assess the condition of the machine by a determined threshold simply. The impulse energy ratio is defined as:

3

λ = \frac{\sum_{n_{1}} {|〈f (x), ϕ_{n_{1}}〉|}^{2}}{\sum_{n} {|〈f (x), ϕ_{n}〉|}^{2}}, n_{1} \in n, n \in Γ,

in which set $n_{1}$ means the index of the Wpsym4-5 atomic types and their projection coefficients, and set $n$ means the index of the all types in the dictionary and their projection coefficients. The impulse energy ratio will indicates fault condition of the PMSMs.

Step 4: after the threshold value of impulse energy ratio is determined, the PMSM condition is assessed by the threshold.

3. Noise and vibration assessment of the PMSMs

3.1. Natural characteristics of the PMSM

Noise and vibration of the elevator traction machine, which is a special external rotor PMSM, is assessed in this section. As shown in Fig. 1, the machine is composed of a stator, a rotor comprised of a rotor support and an axle, and bearings including a rear and a front bearing. The stator is combined by a machine body, a rear end cover and coils. Magnetic poles are distributed evenly in the circumstance of the rotor support. The front bearing is a spherical roller bearing, which endures the primary load of the elevator cabin. From the characteristic structure of the machine, it is noted that noise and vibration is induced by excitation of the bearing rotation and magnetic forces between the rotor and the stator. Vibration waves spread along the structure, and radiate noise on the external surface.

Fig. 1Assembly of the elevator traction machine: 1 – machine body; 2 – rear end cover; 3 – rear bearings; 4 – coils; 5 – rotor support; 6 – front bearings; 7 – axle

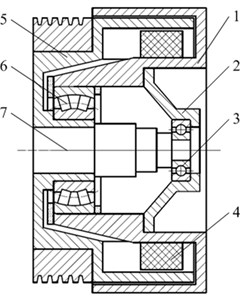
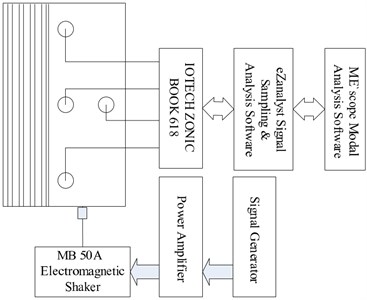
Fig. 2Modal testing setup: a) modal testing site, b) modal testing system

a)

b)

In order to assess the noise and vibration of PMSMs, modal testing should be implemented to obtain natural characteristics of the machines. Fig. 2 shows modal testing setup, of which the exciting point is located on the lateral side of the machine, and the response measuring points are placed on the top of the machine because of its neighboring to the magnetic poles. The 4 single-axis accelerators are selected for the response measurement. Excitation force is exerted using electromagnetic shaker MB 50 A. The IOtech ZonicBook 618E is adopted as the dynamic signal analyzer, and the DG1022 is used as signal generator to generate scanning exciting signal. After 100 times linear averages, the FRFs (frequency response function) are obtained, and then imported into ME’scope modal analysis software for modal analysis.

Table 2 shows the modal frequencies, the modal damping factors and the vibration modes which are obtained from the above modal testing. The open-close vibration mode shapes of the stator body look like the vibration mode shapes that shown in Fig. 3. The 2nd and 3rd vibration modes in Table 1 correspond to Fig. 3(a), and the 4th vibration mode in Table 1 corresponds to Fig. 3(b). Since the body open-close vibration mode shapes of the machine's stator coincide with the radial magnetic forces wave [20], the noise and vibration in the frequency range from 300 to 550 Hz might correspond with the modal characteristics of the machine.

Fig. 3Results of modal analysis using Ansys

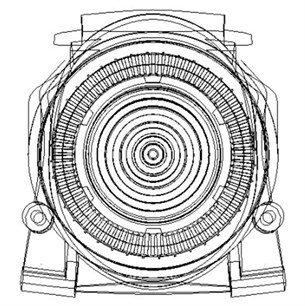
a) 1st mode shape of body open-close

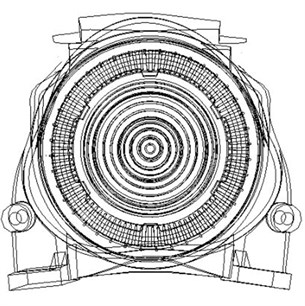
b) 2nd mode shape of body open-close

Table 2Results of modal analysis of the elevator traction machine

Modal order	Natural frequency (Hz)	Modal damping factor (%)	Mode shape
1st	372	0.795	body swing
2nd	517	0.794	body open-close
3rd	549	2.35	body open-close
4th	641	2.5	body swing-open-close
5th	739	1.48	body swing
6th	882	1.65	body swing

3.2. Specification of vibration measurement

Since noise and vibration indicate some failures of the machine in final inspecting process, the vibration measurement experiments are planned in order to diagnose the cause of noise and vibration and improve the manufacturing process. Vibration signals at normal speed are selected to assess noise and vibration of the machine because noise is related to vibration. The specifications of the elevator PMSM are illustrated as follows: normal speed of the machine, $n =$ 168 r/min; pole pairs, $p =$ 20; slot number, $Z_{2} =$ 90; inverter carrier frequency, 8 kHz. The specifications of front spherical roller bearing in the machine are illustrated as follows: number of roller, 27 $\times$ 2; diameter of the rollers, 14.988 mm; diameter of pitch circle, 150 mm; contact angle, 8.5°. The specifications of back ball bearing in the machine are illustrated as followings: number of balls, 10; diameter of balls, 14.288 mm; diameter of pitch circle, 72.5 mm.

Three unqualified elevator PMSMs at different failure levels with respect to the noise and vibration are selected for the vibration measurement. The accelerator 14206 and dynamical signal analyzer IOtech ZonicBook 618E with eZanalyst software are used to pick up the vibration signals. After assessment of the noise and vibration, the vibration signals of the improved elevator PMSM are also collected by the measurement system. All of the sampling rates are set to be 5120 Hz in order to maintain the useful frequency contents. The vibration signals acquisition is done under the sampling configuration in the operation conditions of a free load and a rated machine speed of 168 rpm. At this speed, the characteristic frequencies of the front and the back bearing can be calculated into Table 3. From Table 3, we can find that the bearing characteristic frequencies are much smaller than the modal frequency of the machine. The factors with regard to the resonance effects due to bearing faults can be ignored.

Table 3Characteristic frequency of the front and back bearings

Bearings	RPS¹ (Hz)	BPFO² (Hz)	BPFI³ (Hz)	FTF⁴ (Hz)	BSF⁵ (Hz)
Front bearing	2.8	34.06	41.54	1.26	13.87
Back bearing	2.8	8.68	13.72	1.08	5.9
¹Revolutions Per Second.
²Ball or Roller Pass Frequency of Outer Ring.
³Ball or Roller Pass Frequency of Inner Ring.
³Ball or Roller Pass Frequency of Inner Ring.
⁵Ball or Roller Spin Frequency.

3.3. Analysis of electromagnetic force

Most of the electromagnetic vibration/noise is caused by the radial electromagnetic force waves, which are aroused by the main wave magnetic fields, the harmonic wave magnetic fields, the 1st order teeth harmonic magnetic fields, and the unbalanced magnetic fields [21]. The force wave of main wave magnetic fields can be formulated as:

4

P_{1} = P_{0} \cos (2 p θ - 2 ω_{1} t - 2 θ_{0}),

where $P_{0}$ is the constant of the radial electromagnetic force, $p$ is the pole pairs of the motor, $ω_{1}$ is the angular velocity of main wave, and $θ_{0}$ is initial phase. According to the above mentioned specifications of the MPSM, the frequency of basis wave is:

5

f_{0} = \frac{n p}{60} = 168 \times \frac{20}{30} = 56 Hz,

where $n$ is the rated rotation speed of the MPSM in 168 rpm. Therefore the related harmonic frequencies include the following parts:

1) Rotating harmonic frequency of the rotor:

6

f_{1} = k_{1} p f_{r} = 112, 168, 224, 280, 360, \dots Hz, k_{1} = 1, 2, 3,

2) Teeth harmonic frequency of the rotor:

7

f_{2} = k_{2} Z_{2} f_{r} = 252, 501, \dots Hz, k_{2} = 1, 2, 3, \dots,

3) Interactive frequency between the stator and the rotor:

8

f_{3} = (k_{2} Z_{2} + 2 k_{1} p) f_{r} = 364, 390, 476, 532, 588, 613, \dots Hz, k_{1}, k_{2} = 1, 2, 3, \dots .

The above frequencies coincide with the frequencies in the power spectrum density of the free-load torsion of the elevator PMSM simulated using Ansoft Maxwell 14.0.

3.4. Vibration analysis and assessment based on MP

In this section, matching pursuit algorithm with the above selected atomic dictionary including Daubechies symlet packet atom, DCT-II atom and sine atom is applied to decompose the vibration signals of the elevator MPSMs in both good and bad conditions for the selected PMSMs. Then after the threshold of the impulse energy ratio is determined, the assessment of 25 PMSMs is implemented.

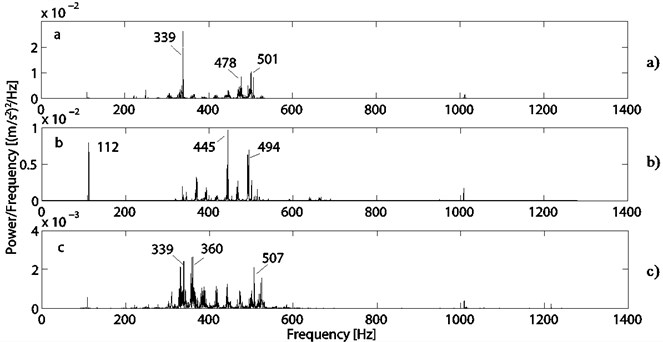
In order to understand the frequency characteristics of the vibration signals, the power spectrum density (PSD) method is used to analyze three elevator PMSMs of different bad conditions, among which No. 1 and No. 2 PMSM are assessed to be unqualified, while No. 3 PMSM is assessed to be qualified by the inspectors. As shown in Fig. 4, the vibration magnitudes of the machine No. 1 and No. 2 are 10 times greater than that of the machine No.3, especially the contents in frequency domain in the range from 300 to 400 Hz and 400 Hz to 550 Hz. All machines have three contents in frequency domain that cover the contents of 112 Hz, 300 to 400 Hz and 400 to 550 Hz. According to the above computed results, these contents in frequency domain correspond with the rotating harmonic frequencies, the teeth harmonic frequencies and the interactive frequencies between the stator and the rotor, respectively. Meanwhile, they also coincide with the natural frequencies of the 1st, 2nd and 3rd swing, open-close mode shapes, respectively. But all these three contents are not relevant to the characteristic frequencies of the bearings.

Fig. 4Power spectrum density of: a) PMSM No. 1, b) PMSM No. 2, c) PMSM No. 3

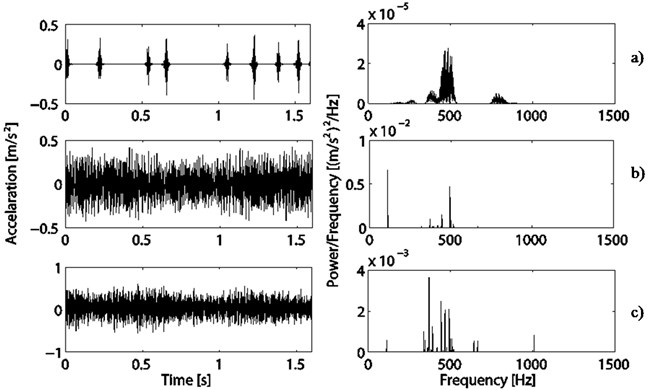
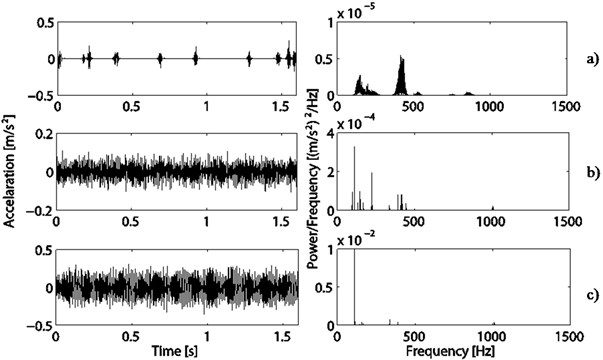
In order to assess the noise and vibration of the elevator PMSMs clearly, the vibration signals of these three machines are decomposed using MP algorithm with the selected atomic dictionary. As shown in Fig. 5-7, the transient contents of the vibration signals are extracted by the Daubechies symlet packet atom, and frequencies of these transient contents exist in the range from 300 to 400 Hz and 400 to 500 Hz. Obviously, these contents coincide with not only the rotating harmonic frequencies, the teeth harmonic frequencies and the interactive frequencies between the stator and the rotor, but also the related natural frequencies. Meanwhile, the intervals of impulse in these three machines are irregular, indicate the complicated transient phenomenon. The extracted contents by DCT-II and Sine atom are steady-state harmonic vibration contents which reflect the electromagnetic force wave in the frequency domain of 112 Hz, 300 to 400 Hz and 400 Hz to 550 Hz, respectively. The magnitude of the steady-state harmonic vibration for the No. 3 machine is obviously less than that of other machines.

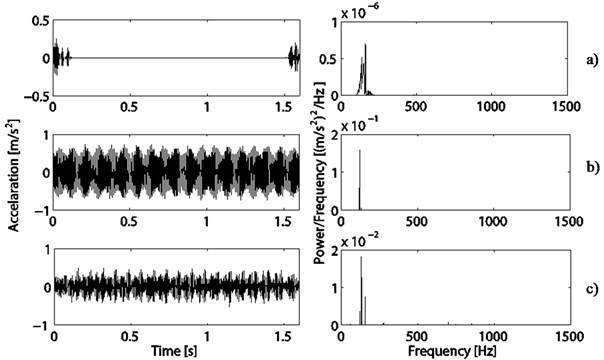
Based on the assessment of noise and vibration, it is concluded that the abnormal electromagnetic forces are the main cause of the abnormal noise and vibration. It is found that the unevenly-placed permanent magnetic poles in the circles of the rotors lead to inconsistent magnetic flux density between each other. Therefore, after being inspected, the permanent-magnetic poles are assembled carefully in order to ensure the consistent flux density. As shown in Fig. 8, the magnitude of the transient contents extracted by the Daubechies symlet packet atom is decreased significantly, and corresponds with the electromagnetic frequencies in 112 Hz and 339 Hz domains. The stead-state contents extracted by the DCT-II and Sine atoms mainly focus on the contents in frequency domain of 112 Hz which is the 1st order rotating harmonic frequency of the rotor.

Fig. 5Decomposition based on MP of the PMSM No. 1: a) Projections on Daubechies symlet packet basis and its PSD, b) Projections on DCT basis and its PSD, c) Projections on sine basis and its PSD

Decomposition based on MP of the PMSM No. 1: a) Projections on Daubechies symlet packet basis and its PSD, b) Projections on DCT basis and its PSD, c) Projections on sine basis and its PSD

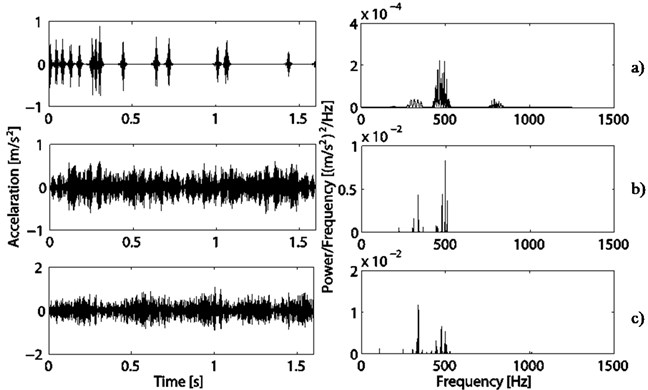
Fig. 6Decomposition based on MP of the PMSM No. 2: a) Projections on Daubechies symlet packet basis and its PSD, b) Projections on DCT basis and its PSD, c) Projections on sine basis and its PSD

Decomposition based on MP of the PMSM No. 2: a) Projections on Daubechies symlet packet basis and its PSD, b) Projections on DCT basis and its PSD, c) Projections on sine basis and its PSD

After the structure of the machine was modified and optimized and the assembly process was regulated, the new-type elevator PMSMs are produced in the factory. As shown in Fig. 9, the transient contents, which are extracted by the Daubechies symlet packet atom, do not nearly exist in considering of the end effects in signal processing. And the steady-state contents extracted by the DCT-II and Sine atom mainly focus on the 1st order rotating harmonic frequency of the rotor in 112 Hz, and high order electromagnetic harmonic nearly do not exist.

Fig. 7Decomposition based on MP of the PMSM No. 3: a) Projections on Daubechies symlet packet basis and its PSD, b) Projections on DCT basis and its PSD, c) Projections on sine basis and its PSD

Decomposition based on MP of the PMSM No. 3: a) Projections on Daubechies symlet packet basis and its PSD, b) Projections on DCT basis and its PSD, c) Projections on sine basis and its PSD

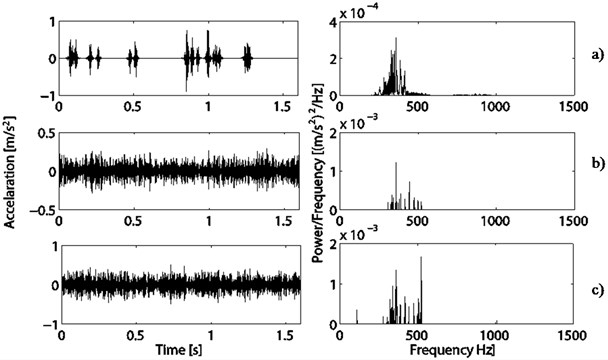
Fig. 8Decomposition based on MP of the PMSM with changed magnetic poles: a) Projections on Daubechies symlet packet basis and its PSD, b) Projections on DCT basis and its PSD, c) Projections on sine basis and its PSD

Decomposition based on MP of the PMSM with changed magnetic poles: a) Projections on Daubechies symlet packet basis and its PSD, b) Projections on DCT basis and its PSD, c) Projections on sine basis and its PSD

So matching pursuit method with carefully selected atom can accurately decompose the vibration signals of the elevator PMSMs, and the extracted transient components can be used to assess and diagnose the cause of the noise and vibration of the elevator PMSMs.

After the above analysis, the impulse energy ratios for the above 4 PMSMs are computed according to Eq. (3), which are 7.5909 %, 8.9375 %, 2.7175 %, 21.6593 % and 0.4049 % for the machine No. 1, No. 2, No. 3 and No. 4 respectively. So the threshold of the impulse energy ratio is set as 1 %. In order to evaluate the assessment method, 20 PMSMs in bad condition and 5 PMSMs in good condition from the PMSM factory are selected for assessment based on the presented assessment scheme. The correct rate of assessment for the machines is 100 %.

Fig. 9Decomposition based on MP of the new-type PMSM: a) Projections on Daubechies symlet packet basis and its PSD, b) Projections on DCT basis and its PSD, c) Projections on sine basis and its PSD

Decomposition based on MP of the new-type PMSM: a) Projections on Daubechies symlet packet basis and its PSD, b) Projections on DCT basis and its PSD, c) Projections on sine basis and its PSD

4. Conclusion

An assessment scheme based on matching pursuit method with selected atoms is presented to diagnose the noise and vibration of the elevator PMSMs. Electromagnetic noise and vibration of the elevator PMSMs are complicated, especially when there exists some distorted magnetic fields, which are induced by many factors, such as over-assembly-tolerance of the permanent magnetic pole. By using Daubechies symlet packet atom, DCT-II atom, and Sine atom, the transient and steady-state components of the vibration signals are successfully extracted respectively. The frequency domain of the extracted transient and steady-state components coincide with the frequencies of the electromagnetic force wave and the natural frequencies of the machine. It is found that the impulse energy ratio using the transient components extracted using Daubechies symlet packet atom can successfully identify the failure degree of the machines, which thus can be used to guide the structure modification and assembly process improvement.

References

Islam R., Husain I. Analytical model for predicting noise and vibration in permanent-magnet synchronous motors. IEEE Transactions on Industry Applications, Vol. 46, Issue 6, 2010, p. 2346-2354.

Search CrossRef
Timar P. L. Noise and vibration of electrical machines. Elsevier, Amsterdam, 2004.

Search CrossRef
Yang S. J. Low-noise electrical motors. Clarendon, Oxford, 1981.

Search CrossRef
Hur J., Kim B. W. Rotor shape design of an interior PM type BLDC motor for improving mechanical vibration and EMI characteristics. Journal of Electrical Engineering and Technology, Vol. 5, Issue 3, 2010, p. 462-467.

Search CrossRef
Zeze E., Akatsu K. Research on vibration analysis and noise-reduction technique of PM motor. Proceeding of 20th International Conference on Electrical Machines, 2012.

Search CrossRef
Sun T., Kim J.-M., et al. Effect of pole and slot combination on noise and vibration in permanent magnet synchronous motor. IEEE Transactions on Magnetics, Vol. 47, Issue 5, 2011, p. 1038-1041.

Search CrossRef
Wu Y. C., Hong Y. C. Cogging torque and torque ripple reduction of a novel exterior-rotor geared motor. Journal of Vibroengineering, Vol. 14, Issue 4, 2012, p. 1477-1485.

Search CrossRef
Goldman S. Vibration spectrum analysis: a practical approach. Second Edition, Industrial Press Inc., New York, 1999.

Search CrossRef
Sonmez D., Seker S., Gokasan M. Entropy-based fault detection approach for motor vibration signals under accelerated aging process. Journal of Vibroengineering, Vol. 14, Issue 3, 2012, p. 1263-1277.

Search CrossRef
Cristalli C., Paone N., et al. Mechanical fault detection of electric motors by laser vibrometer and accelerometer measurements. Mechanical Systems and Signal Processing, Vol. 20, Issue 6, 2006, p. 1350-1361.

Search CrossRef
Antonino-Daviu J. A., Rodriguez P. J., et al. Transient detection of eccentricity-related components in induction motors through the Hilbert-Huang Transform. Energy Conversion and Management, Vol. 50, Issue 7, 2009, p. 1810-1820.

Search CrossRef
Antonino-Daviu J. A., Riera-Guasp M., et al. Toward condition monitoring of damper windings in synchronous motors via EMD analysis. IEEE Transactions on Energy Conversion, Vol. 27, Issue 2, 2012, p. 432-439.

Search CrossRef
Riera-Guasp M., Pineda-Sanchez M., et al. Diagnosis of induction motor faults via Gabor analysis of the current in transient regime. IEEE Transactions on Instrumentation and Measurement, Vol. 61, Issue 6, 2012, p. 1583-1596.

Search CrossRef
Mallat S., Zhang Z. Matching pursuit with time-frequency dictionaries. IEEE Transactions on Signal Processing, Vol. 41, Issue 12, 1993, p. 3397-3415.

Search CrossRef
Mallat S. A wavelet tour of signal processing: The sparse way. Elsevier Inc., 2009.

Search CrossRef
Tang H., Chen J., et al. Signal complexity analysis for fault diagnosis of rolling element bearings based on matching pursuit. Journal of Vibration and Control, Vol. 18, Issue 5, 2012, p. 671-683.

Search CrossRef
Liu B., Ling S. F., et al. Bearing failure detection using matching pursuit. NDT and E International, Vol. 35, Issue 4, 2012, p. 255-262.

Search CrossRef
Feng Z., Chu F. Application of atomic decomposition to gear damage detection. Journal of Sound and Vibration, Vol. 302, Issue 1-2, 2007, p. 138-151.

Search CrossRef
Yoshida H. Matching pursuit with optimally weighted wavelet packets for extraction of microcalcifications in mammograms. Applied Signal Processing, Vol. 5, Issue 3, 1998, p. 127-141.

Search CrossRef
Dai Y., Cui S., et al. Analysis on electromagnetic vibration/noise of induction motors for EV drives. Proceedings of the Chinese Society of Electrical Engineering, Vol. 32, Issue 33, 2012, p. 89-97, (in Chinese).

Search CrossRef
Ma H. Zh. Motor condition monitoring and fault diagnosis. Machinery Industry Press, Beijing, 2008, (in Chinese).

Search CrossRef

About this article

Received

12 January 2014

Accepted

18 March 2014

Published

30 June 2014

Keywords

matching pursuit

permanent-magnet synchronous motors

noise

vibration

Acknowledgements

The work described in this paper is supported by the Major Program of Natural Science Foundation of China (No. 91223201), the Science and Technology Planning Project of Guangdong Province, China (No. 2012B011300010 and No. 2012B091100141), and the Natural Science Foundation of Guangdong Province (No. S2013030013355).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.