Resonant vibration-based evaluation of wood drying defects

1. Introduction

Wood appears to be one of the most widely used materials in building constructions, furniture production and other areas. Depending on exploitation conditions, it has to undergo drying until the required level of moisture is reached. However, the drying process involves more than simply removing excess moisture; when wood is subjected to a drying condition it shows better mechanical properties and more resistance to environmental moisture and temperature fluctuations, ultraviolet rays and etc. In seeking to significantly enhance resistance to environmental exposure, heat-treated wood (thermo-wood) is manufactured, which is heated at 140–240 ^oC.

During the drying and heating process there is uneven distribution of moisture and temperature in wood assortments, which results in the formation of stresses. If they exceed the strength limit, wood assortments develop cracks and in many cases become unsuitable for production.

Mechanical properties of wood products undergo assessment by treating products as distributed parameter systems, i.e. as beams, panels and the like. The extensive distribution of measured parameters is conditioned by internal defects, such as decay, knags, cracks and etc., found in specimens.

The article [1] describes the mechanism of crack formation when capillary porous materials undergo the drying process. A theoretical model was created to describe this effect. It was demonstrated that the acoustic emission method allows to observe and control the drying process, and to select optimal drying parameters (duration and quality). Theoretical and practical experiments were performed when drying cylinder-shaped specimens made of kaolin and pine wood. Theoretical prognoses were based on experimental research. It was shown that the acoustic emission method can be applied when it is necessary to optimize the drying process.

Another article [2] emphasizes that wood drying is an inevitable process during which dried assortments can undergo deformation, develop cracks and etc. There is a direct dependency between mechanical properties of wood, moisture and temperature, which can be expressed in mathematical dependencies. Based on mathematical calculations, it was established why dried assortments with larger cross-section tend to crack more frequently. The modelling reveals that there is different swelling (shrinkage) in separate zones of the assortment. Theoretical models were applied to explain occurring wood deformations.

The article [3] analyses three mathematical models (single board drying model, kiln-wide drying model and drying stress model), in order to simulate softwood drying in kilns and drying induced stresses. The stress model was used for the optimization of the drying regime and the effective reduction of drying induced stresses.

The paper [4] examines how the drying temperature affects wood hardness. After exposing pine wood to convective and microwave drying, results revealed that those assortments that underwent microwave drying at 60–100 ^oC until 8 % moisture was reached showed a significant difference in hardness along the fibre. When drying up to 12 %, there was no noticeable difference in wood hardness. It was found that in contrast to the drying method or temperature, density and moisture have greater impact on wood physical properties.

When exposed to high temperatures, colour change and surface roughness of heated wood depends directly on the drying duration, since the heating process causes changes in the structure of lignin and hemicellulose [5]. When subjected to heating, wood shows more resistance to the environmental exposure and harmful insects.

The study [6] reveals that when exposing various types of wood to 120–200 ^oC heating, the development of cracks can be observed among layers of cell walls (in cell corners). Soft types of specimens tend to crack in a tangential direction in the latewood zone, especially in the case of wood with narrow annual rings, or wood develops cracks in the zone between the earlywood and latewood.

The work [7] provides the modelling of softwood drying at high temperatures. It examines how various factors influence the mechanism of moisture movement and analyzes consistent patterns of liquid migration in cell walls of damp wood. It was established experimentally and theoretically that moisture permeability is affected by the arrangement of growth rings on the cutting surface and wood density (especially in the core).

Another research paper [8] deals with stresses and deformations that develop during the wood drying due to the swelling, shrinkage and external mechanical impact. A wood drying model was created to evaluate hydro, thermo, sorptive and elastic deformations, and their change during the drying process.

The investigations in the field of precise vibromechanics and vibroengineering are more widely known. Various designs of mechanical systems of different types, new principles, innovations and more than 1750 inventions and patents of the author have been developed with co-authors [9].

In the work [10] the vibrations of a multi-layered polymeric film are investigated. It is determinated that upper and lower layers are stiff and do not deform in the transverse direction, while internal layer can deform in the transverse direction. The first four eigenmodes are analysed, graphical results of their investigation are presented.

Resonant oscillations are used to estimate the modulus of elasticity of wood, humidity and other parameters [11].

Thus it has become particularly topical to assess the quality of dried wood assortments, since wood develops cracks during the drying process as a result of occurring stresses.

The objective of this study is to detect cracks in dried wood assortments.

2. Testing Methodology and Equipment

Tests were performed by measuring resonant oscillations of beam-shaped specimens. Investigations deal with rectangular cross-bar resonant oscillations [12] (Fig. 1).

Beam equation of motion is written using the following format:

where $E$ – Young’s modulus; $I$ – area moment of inertia of beam cross section; $\rho$ – density of beam material; $S$ – cross-section area.

Fig. 1Beam chart in testing: x, y – coordinates, l – length of the beam

When the beam stiffness is independent of x coordinates:

where $a=\sqrt{\frac{EI}{\rho S}}$.

Beam transverse oscillation frequency is calculated as follows:

where $k_i=\left(\frac{1}{2}+i\right)\frac{\pi }{l}$.

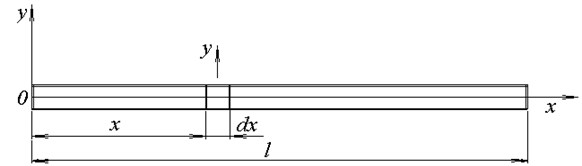
Such beam amplitude-frequency characteristics aggregates of the succession individual resonant vibration modes. First three vibration modes of free beam are shown in Fig. 2.

Fig. 2First three (a, b, c) vibration modes of free beam

When the vibrating beam from the studied wood mode complies with any of the theoretical beam mode, by setting oscillation frequency and other parameters wood modulus of elasticity is estimated [11].

During the moistening/drying and heating/moistening processes, after wood dries and swells, some specimens, owing to the residual stresses, develop relatively large cracks, which can exist prior to the cutting of specimens and become even more noticeable during the thermal treatment (Fig. 3).

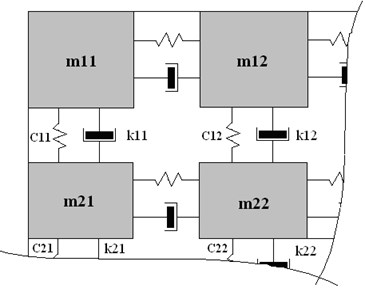
The cracked specimen (Fig. 3) appears to be heterogeneous, i.e. it vibrates as a discontinuous body. This is how the specimen ‘turns’ from the distributed parameter system into the concentrated parameter system with a number of degrees of freedom (Fig. 4) [12].

Fig. 3The scheme of the specimen that developed cracks in various directions: m1, m2, m3 – masses of separate elements of the cracked specimen

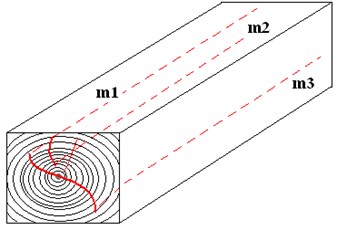
Fig. 4The dynamic model of the cracked specimen: here m11 – mij – masses of specimen’s separate zones, c11 – cij, k11 – kij – rigidity and damping coefficients

Such a system of free oscillations equations, which overlooked damping, is recorded:

Each mass in the form of vibrations recorded harmonic function:

where $p_i$ and ${\phi }_i$ are the frequency and phase angle.

In this case the beam amplitude frequency characteristics become more complex, depending on the mass, stiffness and damping coefficient values.

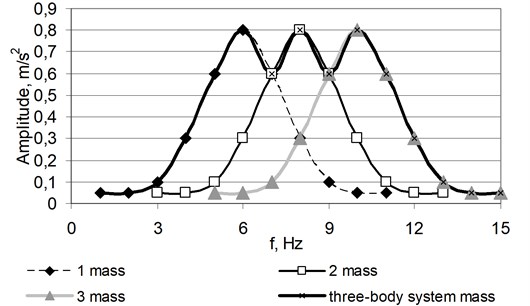
At the same time different resonant frequencies of specimen’s separate elements are recorded (Fig. 5).

Fig. 5Amplitude-frequency characteristic of the specimen composed from three separate elements close to the resonance frequencies and uniform damping rates

3. Simulation of Crack Defects

Tests involved birch and pine wood specimens with the following dimensions: 250×40×25 mm and 300×30×30 mm, respectively. Initially, all samples were fixed amplitude frequency characteristics of the first vibration mode. First mode of beam vibrations is submitted in Fig. 6 [11].

Fig. 6The first mode of beam vibrations

Specimens underwent drying in the air (at 30 ^oC) until 6.5 % moisture was reached. Subsequently birch specimens were subjected to moistening in the air, whereas pine specimens were exposed to water soaking. Then specimens moistened in this manner underwent heating in the air for 3 hours at 120 ^oC – 210 ^oC. Based on the changes in amplitude-frequency characteristics, which were obtained by exposing the specimen to vibration in various (bending) directions, the evaluation of wood cracks was carried out (Fig. 1).

Part of pine wood specimens was used for the modelling of crack defects. In order to simulate possible cracks, cuts were made on various flat surfaces of specimens and changes in amplitude-frequency characteristics were recorded.

As wood develops cracks in various directions, cuts that simulate crack defects were made on all the flat surfaces of pine wood specimens by changing their length and depth. Before introducing the cuts, amplitude-frequency characteristics of specimens were established by exciting transverse resonant vibrations with respect to all the flat surfaces of the specimen (in different directions of specimen bending).

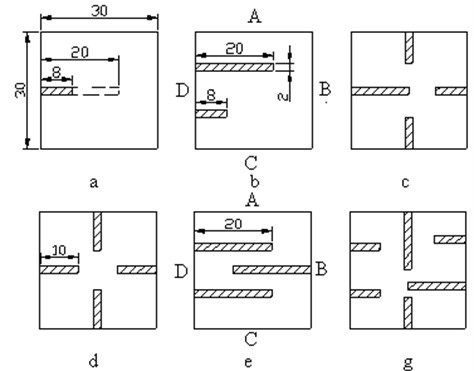
Fig. 7 shows modelling schemes of cracks (defects) of pine wood specimens.

Fig. 7Modelling schemes of crack defects

Initially the cut was made on one of the flat surfaces of the specimen by changing its depth within the range of 8 – 20 mm. It was determined that there is a significant change in the amplitude-frequency characteristic of the specimen, when the depth of the cut reaches more than 15 mm.

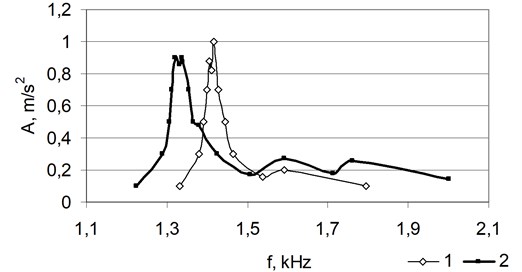
Fig. 8 provides the specific amplitude-frequency characteristic of the specimen (which is analogous in the case of each specimen) prior to and after the modelling of the crack depth.

Fig. 8The amplitude-frequency characteristic of the specimen prior to (1) and after (2) the modelling of the crack depth

Subsequently, the selected depth of the cut was 15 mm and the length was altered within the range of 75 – 300 mm. It was found that the length of the cut had no significant impact on the amplitude-frequency characteristic of the specimen; the change occurs, when the length reaches 150 mm. The cut made along the entire length of the specimen leads to no considerable changes in the amplitude-frequency characteristic (Fig. 9).

Fig. 9The amplitude-frequency characteristic of the specimen in different bending directions by altering the length of the cut

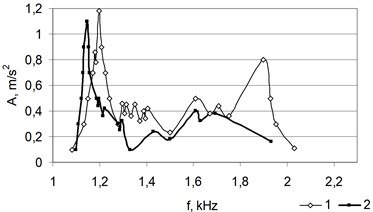
There were more noticeable changes in the amplitude-frequency characteristic of the specimen, when the specimen had several simulated crack defects with various depths (Fig. 7b, c, g, Fig. 10 shows their amplitude-frequency characteristics). It was observed that when all the flat surfaces of the specimen have the same cuts (Fig. 7d), changes in the amplitude-frequency characteristic seem to be minor, whereas, when there is a larger number of cuts and their arrangement is asymmetric, there are major changes in the amplitude-frequency characteristic (Fig. 7c, g).

It can be noticed (Fig. 8, 9 and 10) that the disintegration of the specimen’s structure leads to changes in the amplitude-frequency characteristic. Each part of the specimen has a different resonant frequency. In the present case, the specimen consists of several parts (in separate cases up to 8) of the concentrated parameter system (Fig. 4) and it is impossible to test it as a continuous body.

Fig. 10The amplitude-frequency characteristic of the specimen with several cuts in various bending directions

4. Test Results

Since deciduous and coniferous wood absorbs moisture at different rates, birch and pine wood specimens underwent moistening under different conditions.

Fig. 11 provides amplitude-frequency characteristics of some birch specimens after moistening and heating operations.

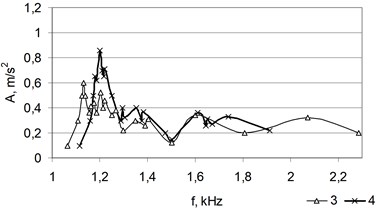
Fig. 11Amplitude-frequency characteristics of different birch wood specimens that cracked during the moistening and heating

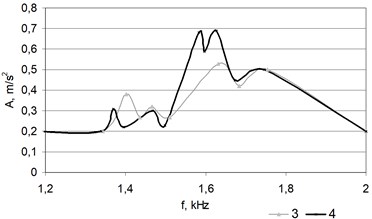
It can be observed that amplitude-frequency characteristics of the first, second, third and fourth birch specimen have the following peaks: 6, 7, 4 and 5, respectively. It is obvious that during the moistening and drying processes specimens split accordingly into a certain number of separate parts.

Analogous results were obtained when moistening and drying pine wood specimens.

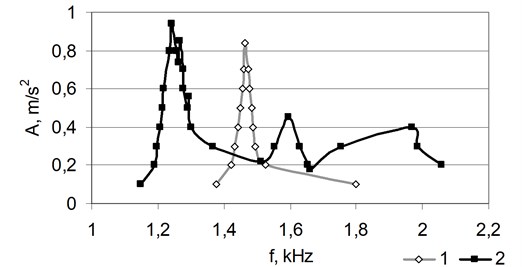
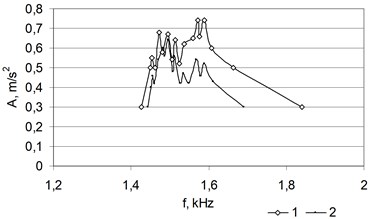
Fig. 12 provides the amplitude-frequency characteristic of the typical pine wood specimen in various bending directions.

Fig. 12Amplitude-frequency characteristics of the moistened-dried pine wood specimen in various bending directions

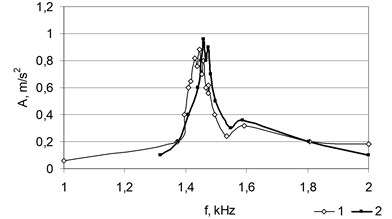
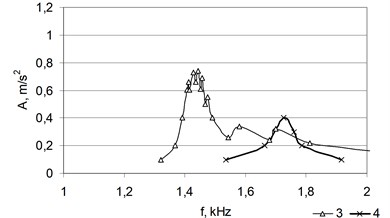
Obtained results show (Fig. 11 and 12) that in an analogous manner to crack modelling it is possible to destroy the structure of specimens during the drying process. The specimen becomes heterogeneous and it consists of several bodies with certain masses and vibrates as a complex system of concentrated parameters. This enables to establish the inner structure of such assortments, i.e. to evaluate cracks and at the same time the quality of drying.

Changes in amplitude-frequency characteristics of specimens were assessed during the modelling of cracks and when wood specimens underwent heating and drying under strict regimes.

Test results can be used for evaluating the quality of dried wood and its sorting.

5. Conclusions

1. It was established that due to the wood cracks, which are developed during the heating and drying process, the distributed parameter system of the vibrating specimen turns into the concentrated parameter system with a number of degrees of freedom.

2. It was obtained that when modelling wood cracks in the specimen its amplitude-frequency characteristic is analogous to the one of the cracked specimen.

3. It was determined that a significant change in the amplitude-frequency characteristic of the specimen occurs, when the depth and length of the modelled crack defect reaches half of the value of the respective dimension.

4. It was found that when the specimen vibrates in different directions, a different amplitude-frequency characteristic is obtained, which allows foreseeing the direction of crack development.

5. The provided methodology enables to assess the inner structure of the wood specimen and the quality of its drying process.