Fault diagnosis of planetary gearbox with multi-channels vibration data based on a novel feature extraction method and LSSVM

2.1. MRSVD

MRSVD is an improved signal processing method based on SVD [9]. SVD requires the construction of a phase space with high dimensions, which leading to dimensional disasters and high computational complexity. The phase space of MRSVD is built by recursion, and multi-resolution SVD is applied to obtain an approximate signal and detail signals, as shown in Fig. 1.

Fig. 1The process of the MRSVD

The detailed decomposition process of MRSVD for time series $V=(v_1,v_2,\dots ,v_N)$ is as follows.

A two-dimensional Hankel matrix is built:

The singular value decomposition of $H_1$ can be described as:

where, $A_1$ and $D_1$ are the approximate signal and detail signal of the first decomposition, respectively, ${\sigma }_{11}$ and ${\sigma }_{12}$ are the two singular values of the first decomposition, ${\sigma }_{11}>{\sigma }_{12}$.

According to the process shown in Fig. 1, the approximate signal can be iteratively decomposed as:

The original signal can be decomposed into an approximate signal and several detailed signals that describe the original signal at different scales. The MRSVD method does not lead to dimensional disasters, because only a two-dimensional Hankel matrix is required to decompose in each iteration. Therefore, MRSVD has an advantage in terms of calculation speed.

2.2. VMD

VMD is a signal-processing method suitable for nonlinear and nonstationary signals. A signal can be decomposed into several IMFs that contain its own central frequency and frequency bands [16].

The model of the VMD can be described as:

where, $f\left(t\right)$ is the original signal in the time domain, $u_i\left(t\right)$ represents the $i$-th IMF of the original signal, ${\omega }_i$ is the center frequency of $u_i$, $K$ is the number of IMFs, ${\partial }_t$ represents the calculation of the partial derivatives of time, $\delta \left(t\right)$ is the unit pulse function.

The extended Lagrangian function is applied to solve Eq. (4) as:

where $\alpha$ is the penalty factor, $\eta$ represents the Lagrange multiplier.

The saddle point of Eq. (5) can be searched by updating $u_i$ and ${\omega }_i$ as follows:

During the iterative solution of the VMD, the center frequency and bandwidth of each IMF are updated until the iteration termination condition is satisfied.

2.3. Dispersion entropy

Dispersion Entropy (DE) is an index that reflects the complexity or irregularity of a time series. The detailed calculation process of DE for the time series $X=(x_1,x_2,\dots ,x_N)$ is as follows:

Step 1: Time series $X$ is mapped to the range of 0 to 1 using a normal distribution function as follows:

where, ${\sigma }^2$ is the variance value of the time series, $\mu$ is the mean value of the time series.

Step 2: Series $Y=(y_1,y_2,\dots ,y_N)$ continues to be mapped to different categories as follows:

where, $R$ is the rounding function, $c$ is the number of categories.

Following the above two steps, each element of the time series $X$ is mapped to the categories $(\mathrm{1,2},\dots ,c)$.

Step 3: The embedding vector $z_j^{m,c}$ is built as follows:

where, $m$ and $d$ are the embedding dimension and time delay respectively.

Step 4: The dispersion pattern is described as follows:

As the dispersion pattern is composited of $m$ bits, and each bit can be formed from 1 to $c$. The number of dispersion patterns is $c^m$.

Step 5: The relative frequency of each dispersion pattern is calculated as follows:

where, the $\mathrm{N}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\left({z_j}^{m,c}\right|{\pi }_{v_0{v}_1\cdots v_{m-1}})$ represents the number of embedding vectors $z_j^{m,c}$ mapped to the dispersion pattern.

Step 6: The dispersion entropy value is calculated according to Shannon Entropy as follows:

The DE value represents the degree of irregularity. DE can obtain the maximum value $\mathrm{l}\mathrm{n}\left(c^m\right)$ when each dispersion entropy has the same probability, such as a noise signal. DE can obtain the minimum value for the periodic signals.

4.1. The fault diagnosis information of planetary gearbox

The failure dataset of the planetary gearbox used in this study was provided by Liu et al. in their research [5]. The failure dataset was collected from a wind turbine drive test rig consisting of a planetary gearbox, motor, fixed-shaft gearbox, and load. The planetary gearbox consisted of four planet gears and a sun gear. The planetary gearbox operates under five different conditions: normal, gear with a broken tooth, wear gear, crack occurs in the root, and missing one tooth. The planetary gearbox parameters are presented in Table 1.

The vibration datasets collected by the acceleration sensors in the $X$ and $Y$ directions were applied for fault diagnosis to verify the proposed method in this study. The time-domain waveforms of the vibration data under five different operating conditions are shown in Fig. 3.

As shown in Fig. 3, the time-domain feature cannot be used to distinguish between different operating conditions.

The vibration data in the $X$ and $Y$ directions were divided into 100 groups of sample sets for each operation condition without repetition, and each group of sample sets included 4096 sample points. In this study, the sample sets were used for feature extraction and fault diagnosis.

Fig. 3The time-domain vibration data of the planetary gearbox in five different conditions

a) Normal

b) Gear with a broken

c) Missing one tooth

d) Wear gear

e) Crack occurs in the root

4.2. Analysis of the proposed IMRSVD

In a rotating system, fault characteristics are often reflected in the frequency. The power spectrum was used to observe the relationship between the fault type and characteristic frequency. In this section, the wear gear vibration data are analyzed as an example. The time-domain waveform and the power spectrum are shown in Fig. 4.

As shown in Fig. 4, the peak value of the power spectrum was approximately 4260 Hz. The rotating and meshing frequencies can hardly be found, and the power spectral density (PSD) of the characteristic frequency is almost submerged.

Fig. 4Time-domain waveform and power spectrum of the wear gear vibration data

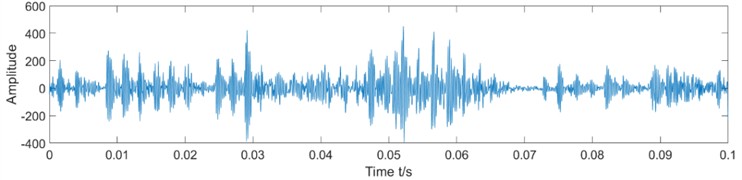
a) Time-domain waveform

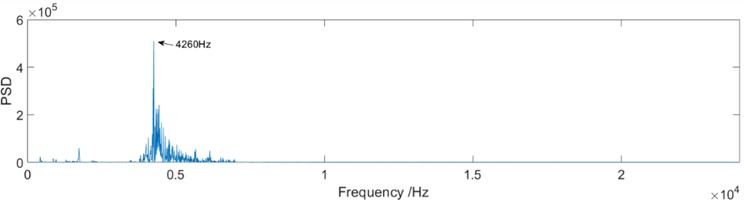
b) Power spectrum

Therefore, the proposed IMRSVD method was applied to process the original vibration signal. The time-domain waveform and power spectrum of the wear gear vibration signal processed by IMRSVD are shown in Fig. 5.

Fig. 5Time-domain waveform and power spectrum of the wear gear vibration signal after IMRSVD processing

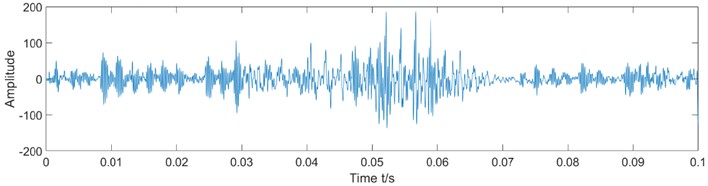
a) Time-domain waveform

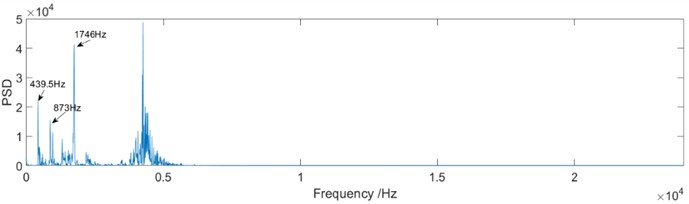
b) Power spectrum

As shown in Fig. 5, the characteristic frequency is displayed after IMRSVD processing. Several characteristic frequencies were obtained, such as 439.5 Hz, 873, and 1746 Hz. As stated above, the meshing frequency of the planetary gearbox was 437.5 Hz, and the observed characteristic frequencies represented the basic frequency and harmonics. The results indicate that the IMRSVD method can effectively remove interference and extract useful features that reflect the operation characteristics of the planetary gearbox.

4.3. Analysis of feature extraction

Because the DE value of the vibration signal can reflect the complexity and variation of the signals, it can be used as a feature for fault diagnosis. In this section, features based on the DE value of the sample set with different composition structures are analyzed.

Firstly, the DE values of the vibration data in the $X$ and $Y$ directions were calculated. The results are shown in Fig. 6.

Fig. 6The DE value of vibration signal under different operating conditions

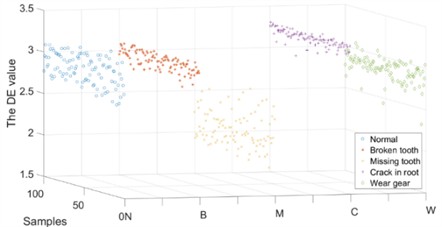
a)$X$ channel

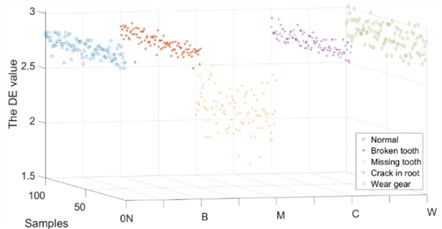
b)$Y$ channel

It can be observed that the DE value of the original vibration signal shows little difference under different operating conditions. Missing tooth conditions can be classified using DE values. However, the other four operating conditions were difficult to distinguish. Therefore, the single DE feature of the original vibration signal is not suitable for fault diagnosis of planetary gearboxes.

As stated in Section 4.2, the vibration signal has several characteristic frequencies, and VMD is utilized to decompose the original vibration signal. The decomposition performance of the VMD is significantly affected by the modal number $K$ and control parameter $\alpha$. In this paper, the center frequency method and minimum envelope entropy were applied to determine the modal number $K$ and control parameter $\alpha$.

Firstly, the initial value of $\alpha$ was set to 2000, and the center frequencies under different modal numbers $K$ are listed in Table 2.

The results show that model mixing appears when the modal number is set as 6, and the modals with center frequency of 4246.69 Hz and 4808.43 Hz are too close. The decomposition performance was better when the number of modal was five.

Secondly, the initial value of $K$ was set to 5, and the envelope entropy of the IMFs with different control parameters $\alpha$ was calculated. $\alpha$ with the minimum envelope entropy is a suitable control parameter. Based on the analysis, the parameters were set to $K=\text{5}$ and $\alpha =$ 1723.

The decomposition results of the wear gear vibration signal are shown in Fig. 7, and the results of the wear gear vibration signal after IMRSVD processing are shown in Fig. 8.

Fig. 7The IMFs and Its PSD of the wear gear vibration signal

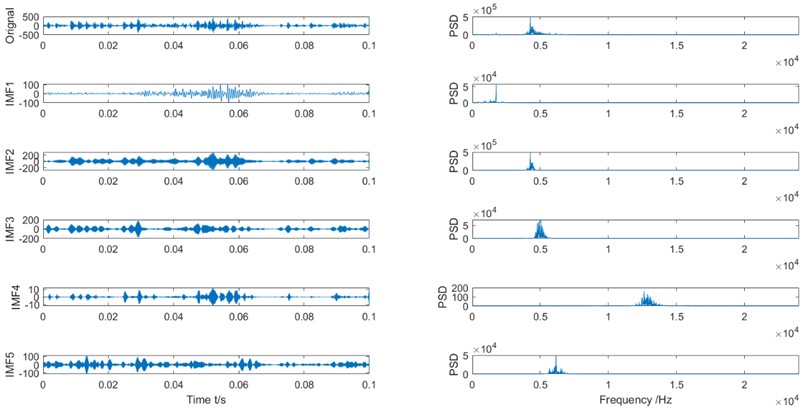
Fig. 8The IMFs and Its PSD of the wear gear vibration signal after IMRSVD processing

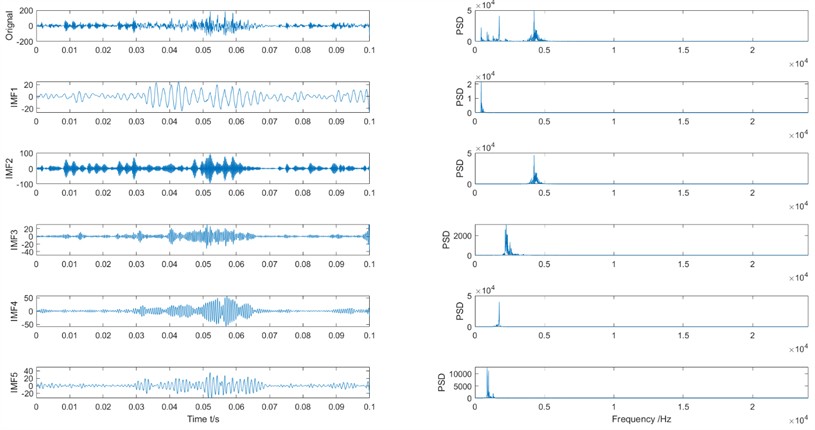
It can be seen that the VMD can decompose the original signals into IMFs with different frequency characteristics. The center frequency of the IMFs of the original vibration signal has little relationship with the characteristic frequency, which means that the original vibration signal has many interfering components. As shown in Fig. 8, the signal after IMRSVD processing contains more characteristic frequencies. The center frequency of the IMFs represents the characteristic frequency of the planetary gearbox, which means that the IMFs have useful information for fault diagnosis. The results further proved the effectiveness of the proposed IMRSVD method.

Because the IMFs contain different characteristic frequencies, the DE of the IMFs can be used as a feature for fault diagnosis. Some of the DE values of the IMFs of the $X$ and $Y$ direction samples under different operating conditions are shown in Figs. 9-10.

The DE values of different IMFs under different operating conditions have differences and connections as well as performance in the $X$ and $Y$ directions. Therefore, a composite feature formed by the DE values of different IMFs in different directions was proposed for fault diagnosis.

Fig. 9The DE value of the IMFs in X channel

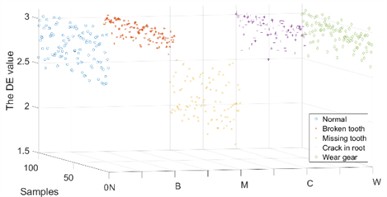
a) IMF 1

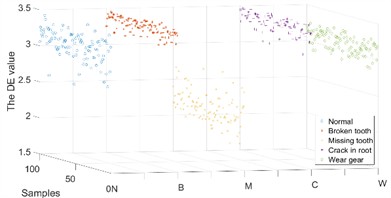
b) IMF 2

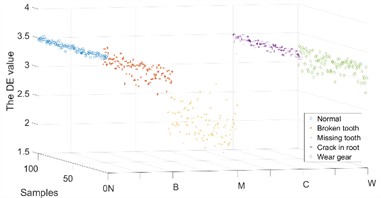
c) IMF 3

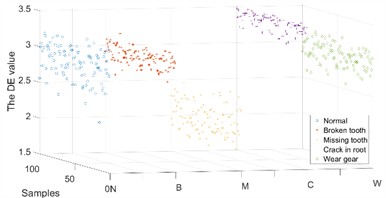
d) IMF 4

Fig. 10The DE value of the IMFs in Y channel

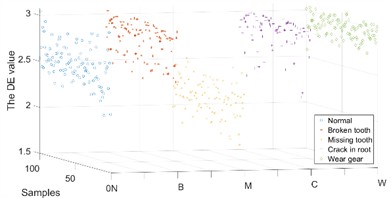
a) IMF 1

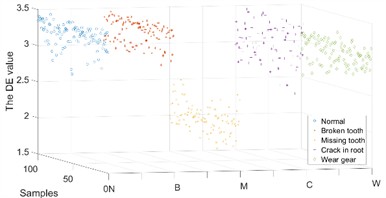
b) IMF 2

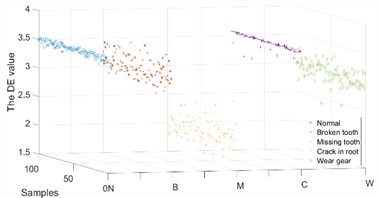
c) IMF 3

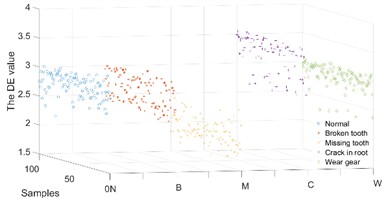
d) IMF 4

4.4. Analysis of the proposed fault diagnosis method

The verification of the proposed fault-diagnosis method is presented in this section. A Back propagation (BP) neural network, SVM, and LSSVM were applied for fault classification. BP and SVM refer to the functional functions built into MATLAB. The BP parameters were set as follows: hidden layer = 20, learning rate = 0.001, and training time = 1000. The RBF kernel function was selected for the SVM. The toolbox LSSVMlabv1_8_R2009b_R2011a was utilize according to http://www.esat.kuleuven.be/sista/lssvmlab. This toolbox has ‘tunlssvm’ function for cross validation optimization of hyper parameters of LSSVM model which is very convenient to use.

Because the classification methods applied in this study are machine learning algorithms, the sample datasets were divided into training and testing sets. The training set was formed using the vibration data and operation labels of the 60 groups of sample sets for each operation condition. The remaining 40 groups of sample sets for each operating condition and their labels were used as testing sets. The classification of the sample data is presented in Table 3.

4.4.1. The performance of IMRSVD for fault diagnosis

The fault diagnosis results with and without IMRSVD were compared to verify the effectiveness of IMRSVD in the proposed method. Except for the difference in signal processing using IMRSVD, the fault diagnosis process for comparison is shown in Fig. 2. Firstly, VMD was applied for the signal decomposition of the double-channel vibration signal. Secondly, DE is utilized for the feature extraction of the IMFs. Finally, the LSSVM was used for classification under different operating conditions. Confusion diagrams of the fault diagnosis results are shown in Fig. 11.

The results showed that the diagnostic accuracy without IMRSVD was 97 %. There were four normal conditional samples, and two crack samples were classified into the broken tooth condition. The proposed method with the IMRSVD process classified all the samples correctly, and the diagnostic accuracy was 100 %. The results indicate that IMRSVD can improve diagnosis accuracy.

Fig. 11The confusion diagram of fault diagnosis

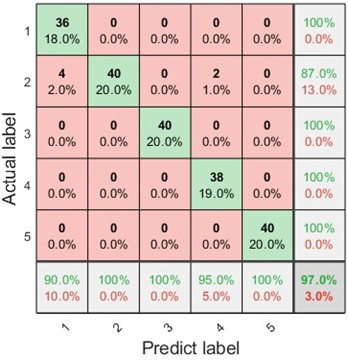
a) Without IMRSVD

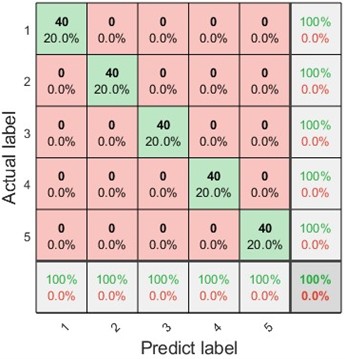
b) With IMRSVD

4.4.2. The performance of different entropy for fault diagnosis

The fault diagnosis efficiency based on different entropies was also discussed. SE and PE were applied to replace DE in the proposed method. Confusion diagrams of the fault diagnosis results based on the SE and DE are shown in Fig. 12.

As shown in Fig. 11(b) and Fig. 12, the diagnostic accuracies based on SE, PE, and DE were 99 %, 99 %, and 100 %, respectively. The results indicate that the DE-based method is more suitable than the proposed fault diagnosis method.

Fig. 12The confusion diagram of fault diagnosis with different entropy

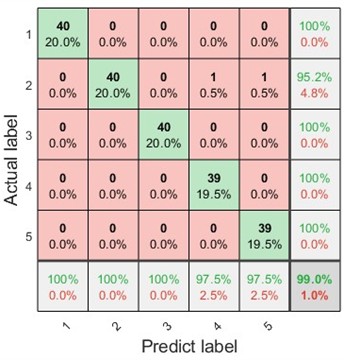
a) SE

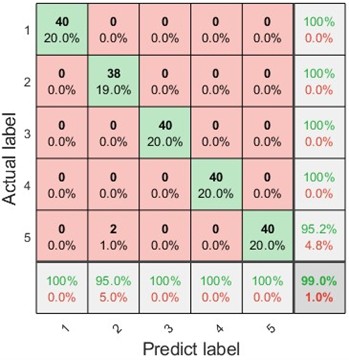
b) PE

4.4.3. The effect analysis of different signal source for fault diagnosis

The accuracies of fault diagnosis using single-channel vibration data and multi-channel vibration data using the proposed method were compared. Confusion diagram of the fault diagnosis results with the single-channel vibration data is shown in Fig. 13.

Fig. 13The confusion diagram of fault diagnosis by single channel vibration data

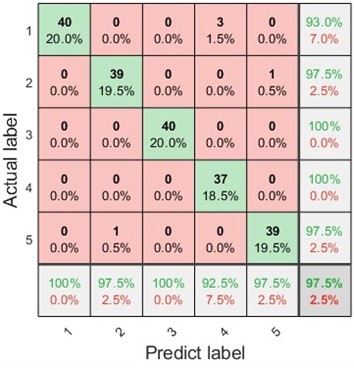
The results show that five samples were misclassified in the fault diagnosis using a single-channel signal. As shown in Fig. 11(b) and Fig. 13, the proposed method with multichannel signals has higher accuracy.