A Zhu-Wang-Tang damage constitutive model for sintered NdFeB considering crack spacing

1. Introduction

Sintered NdFeB rare earth permanent magnet materials are functional materials that were discovered by Sagawa [1] in the 1980s. This material possesses excellent magnetic properties and has spurred the development of industries and technologies like computer hard disk technology, nuclear magnetic resonance, and scanners [2]. Sintered NdFeB serves as energy storage devices that enable efficient conversion of energy and information. Consequently, the volume of NdFeB required to generate the same magnetic field is smaller compared to other magnets, which aligns well with the contemporary demands for lightweight and integrated production. During the manufacturing process and practical applications, these materials inevitably encounter impact loads, making it essential to investigate the dynamic response of sintered NdFeB.

Sintered NdFeB has fundamental mechanical properties that include bending strength, compressive strength, elastic modulus, fracture toughness, and hardness [3, 4]. Many scholars have conducted research on its basic mechanical properties. Szymura et al. [5] examined S-NdFeB permanent magnets with different compositions and found that impact strength, bending strength, and fracture toughness increased with the enhancement of coercivity. Wang Huanran et al. [6] used a split Hopkinson pressure bar to investigate the fracture of NdFeB magnets under uniaxial compression. While these studies primarily focus on the basic mechanical properties of NdFeB, no damage constitutive equations have yet been established to describe the dynamic behavior of sintered NdFeB. Therefore, its dynamic damage constitutive equation requires further exploration.

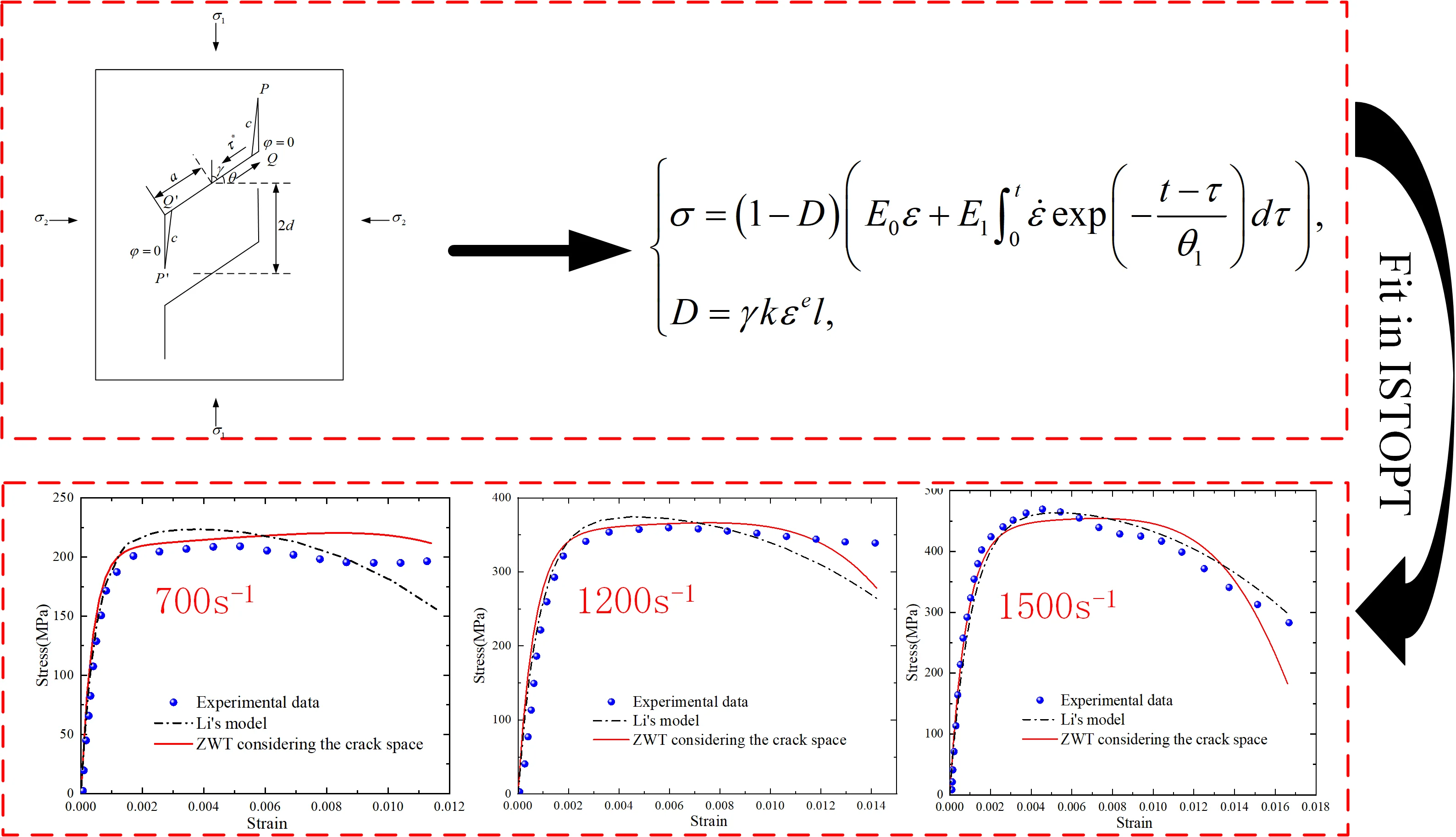
Li et al. [7] conducted experiments on the dynamic characteristics of sintered NdFeB and proposed a damage constitutive model. However, it did not consider the influence of crack spacing in the damage process. Therefore, this paper first fully considers the influence of crack spacing in the damage process, and constructs the damage model of sintered NdFeB based on the weibull distribution and the swing crack growth model. Then, the damage evolution process was combined with the ZWT constitutive model to establish the ZWT damage constitutive model (ZWTDCM). Based on previous dynamic mechanical characteristics tests of sintered NdFeB, ZWTDCM of sintered NdFeB was fitted. Finally, the newly established model was compared with the model proposed by Li. The comparison results fully demonstrated the rationality of the newly established model.

2. Damage constitutive model

2.2. Wing crack propagation model considering crack spacing

The condition for crack propagation under impact is [9]:

3

$K_{ID}=K_{IC}^d,$

where, $K_{IC}^d$ is the fracture toughness. The expression for dynamic stress concentration factor $K_{ID}$ is [10]:

4

$\begin{array}{l}k\left(\dot{l}\right)=\left(1-\frac{\dot{l}}{{\dot{l}}_m}\right){\left(1-\frac{\dot{l}}{2{\dot{l}}_m}\right)}^{-1},\\ {\dot{l}}_m\approx 0.4l_R,\\ K_{ID}=k\left(\dot{l}\right)K_I,\end{array}$

where, ${\dot{l}}_m$ is the maximum crack propagation speed, and $l_R$ is the Rayleigh wave speed. From Eq. (4), $\dot{l}$ can be obtained:

5

$\dot{l}={\dot{l}}_m\left(1-\frac{K_{IC}^d}{2K_I-K_{IC}^d}\right).$

Fig. 1 shows the equivalent representation of the microstructure of sintered NdFeB, where ${\sigma }_1$ and ${\sigma }_2$ represent the far-field loads applied to a single crack, and the initial length of the crack is 2$a$. When the stress concentration factor at the tip of the micro-crack reaches the fracture toughness, frictional slip occurs at points $Q$ and $Q^{\text{'}}$, resulting in the formation of new tensile cracks $P$ and $P^{\text{'}}$. The initial nucleation direction of the tensile cracks makes an angle ($\phi$) with ${\sigma }_1$. As the cracks propagate, the nucleation direction eventually becomes parallel to ${\sigma }_1$.

Fig. 1Wing crack propagation model

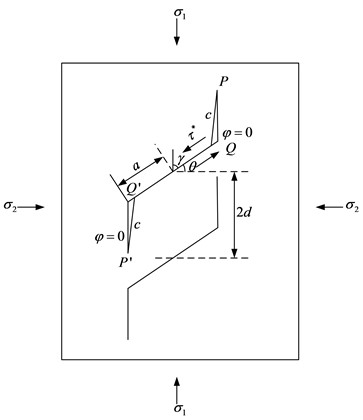
Under the action of far-field loads, $K_I$ at the tip of an I-type crack, considering the spacing of micro-cracks, is given by [11]:

6

$\begin{array}{l}{K}_I=\frac{F\mathrm{s}\mathrm{i}\mathrm{n}\theta }{\sqrt{d\mathrm{s}\mathrm{i}\mathrm{n}\frac{\pi \left(l+l^{\mathrm{*}}\right)}{d}}}-{\sigma }_2\sqrt{2d\mathrm{t}\mathrm{a}\mathrm{n}\frac{\pi l}{2d}},\\ F=2l{\tau }^{\mathrm{*}}=2l\left\{\frac{1}{2}\left({\sigma }_1-{\sigma }_2\right)\mathrm{s}\mathrm{i}\mathrm{n}2\theta -\frac{1}{2}f\left[\left({\sigma }_1+{\sigma }_2\right)-\left({\sigma }_1-{\sigma }_2\right)\mathrm{c}\mathrm{o}\mathrm{s}2\theta \right]\right\},\\ l^{\mathrm{*}}=0.27l,\end{array}$

where, $F$ is the normal force on the crack surface, ${\tau }^{\mathrm{*}}$ is the driving force for crack sliding, and $f$ is the friction coefficient.

2.4. Comparative analysis of the results from the two damage constitutive models

Referring to the experimental results in [7], the parameters of the newly established model were fitted in ISTOPT. Table 1 shows the fitted parameters. From the fitting results, it can be observed that the fitting accuracies of the new model at strain rates of 700, 1200, and 1500 are 0.99, 0.94, and 0.96, respectively, while Li's model has fitting accuracies of 0.97, 0.96, and 0.95 at the same strain rates. The two models show little difference in fitting accuracy, both exhibiting good fitting performance. The comparison of the two models is shown in Fig. 2.

Fig. 2Comparison of the two models

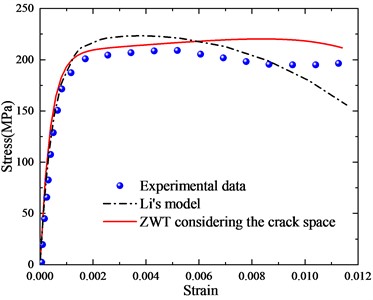
a) 700 s^-1

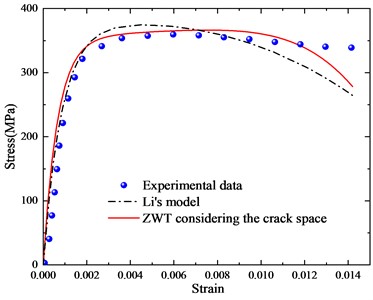
b) 1200 s^-1

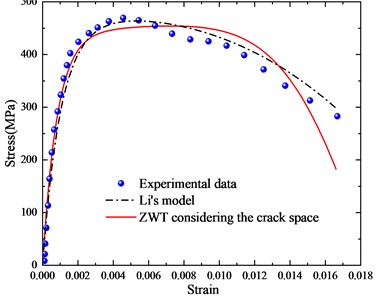
c) 1500 s^-1

In the initial stage, the experimental stress-strain curves are nearly linear, and during this phase, both models can fit the trend of the changes quite well. Subsequently, the stress-strain relationship exhibits nonlinear behavior, at which point both models show some deviation from the experimental data, but the errors remain within a reasonable range. Therefore, it can be seen that the trends in strain change for both models are also consistent with the expected patterns. Thus, the accuracy and rationality of ZWTDCM established in this paper, which considers the effect of crack spacing, have been thoroughly validated.

Table 1Parameters for the new model

Parameters	Values	Parameters	Values
$k$	4×109	2$a$ (μm)	5
$e$	2.5	$\theta$	$\pi$/4
$K_{IC}$ (Pa/m)	4×106	$d$ (μm)	120
$f$	0.7	$E_0$(MPa)	538330
$E_1$ (MPa)	2000	${\theta }_1$ (μs)	0.55

3. Conclusions

In this paper, the influence of crack spacing in the damage evolution process is fully considered, and the damage evolution process of sintered NdFeB is given by combining the Weibull distribution with the swing crack growth model considering crack space. In addition, the ZWT damage constitutive model was constructed by combining the damage process with the ZWT constitutive model. Based on previous experimental data on the dynamic mechanical characteristics of sintered NdFeB, the parameters of ZWTDCM are determined and ZWTDCM was compared with Li’s model. On the one hand, the two models have high fitting accuracy; on the other hand, both can reflect the stress-strain laws of sintered NdFeB under impact. However, compared with Li’s model, this model fully considers the influence of crack gaps during the damage process, so the accuracy and superiority of this model have been further verified.