Feature extraction of rolling bearing based on adaptive variational multi-harmonic mode extraction

Wang, Zhenhu; Liu, Chaozhong

doi:10.21595/jve.2024.24435

Journal of Vibroengineering

Browse Journal

Submit article

Published: 22 January 2025

Check for updates

Feature extraction of rolling bearing based on adaptive variational multi-harmonic mode extraction

Zhenhu Wang¹

Chaozhong Liu²

^{1, 2}Department of Engineering, Huanghe University of Science and Technology, Zhengzhou, 450000, China

Corresponding Author:

Zhenhu Wang

Cite the article Download PDF

Article in Press

Downloads 19

Abstract

Variable multi-harmonic mode extraction (VMHME) not only has the advantages of high computational efficiency and extraction accuracy similar to variational mode extraction (VME), but also could extract the multi-harmonic components of periodic narrowband impulse signals in frequency band as wide as possible, making it very suitable for feature extraction in the event of rolling bearing failure. VMHME needs to accurately estimate the fault characteristic frequency of rolling bearing as its prior parameter, and small errors in estimating the fault characteristic frequency will cause significant deviations in the target extraction components. At present, the theoretical fault characteristic frequency of rolling bearings is commonly used as the estimated fault characteristic frequency. However, due to the installation deformation of rolling bearings and the random sliding between the rolling elements and the raceway during operation, it can cause a deviation between the actual fault characteristic frequency and the theoretical fault characteristic frequency. The most scientific and effective method is to enable VMHME to adaptively obtain the fault characteristic frequency based on the characteristics of the analyzed signal itself. Therefore, this paper introduces the envelope harmonic product spectrum (EHPS) theory into VMHME and proposes an adaptive VMHME (AVMHME) method to effectively extract the multi harmonic components of the periodic narrowband impulse signal when rolling bearings fail. Feasibility of the proposed method is verified through simulation and rolling bearing’ early weak fault experiment, and its superiority is also verified through comparative analysis.

1. Introduction

As one of the most commonly used rotating components in machinery, rolling bearing causes about 45%-55% rotating machinery failures according to the statistics [1]. Effective fault feature extraction techniques could capture the weak fault of rolling bearings timely to avoid potential economic losses. The vibration signal will take on periodic transient impulses when fault arises in rolling bearing, and this typical characteristic is very weak due to the influence of noise and the energy attenuation during transmission.

There are roughly three study directions currently in terms of rolling bearing’ feature extraction: 1) Complex signal decomposition technology: decomposing the original complex vibration signal of rolling bearing into series of single component signals, and then performing feature extraction on the selected single component. 2) Periodic weak impulse signal enhancement technology. 3) Optimal frequency band selection technology to achieve optimal envelope effect. One typical representative method of the first direction is EMD technology [2], which has drawbacks of mode mixing and weak mathematical theoretical support. Although the EMD improved methods [3-5] avoid the mode aliasing problem of EMD effectively, most of them has the disadvantage of high computational complexity. The other mode decomposition methods such as local mean decomposition [6], symplectic geometry mode decomposition [7], variational mode decomposition [8] and so on have the disadvantage of manually setting the number of mode decomposition and selecting decomposition component based on experience for subsequent feature extraction. The later proposed VME method avoids the disadvantage of VMD requiring predetermined number of mode decomposition, which is very likely to cause leakage of harmonic components of the impulse components [9]. The basic theory of the second study direction is to enhance the periodic impulse components, and blind deconvolution (BD) is one typical technology. The pioneer of BD is minimum entropy deconvolution (MED) [10], which uses the kurtosis maximization criterion to search an optimal finite impulse response filter to filter the original vibration signal. To overcome the kurtosis’ sensitive to transient shock outliers, different kinds of BD methods based on the other optimization index such as Gini, $L_{p} / L_{q}$ and so on are proposed and used in repetitive impact enhancement [11-15]. The third research direction is actually to find the optimal resonance frequency band to obtain the best envelope effect, in which series of related methods such as spectral kurtosis [16, 17], fast kurtogram [18], protrugram [19], infogram [20], autogram [21] and so on have been arising. These methods could find the optimal key parameters (Center frequency and bandwidth) to construct a band-pass filter, then filter the original signal by the constructed band-pass filter using the optimal key parameters, at last apply envelope spectral on the filtered signal to extract features. Though the third research direction has achieved a number of successful applications, the in-depth usage of envelope information and the elimination of in-band noise still remain as deficiencies [22].

The periodic impulse characteristic components may be distributed over wide and different frequency bands when failure arises in rolling bearing, and the most ideal approach is to construct a bandpass filter bank based on the center frequency and bandwidth for each frequency band, then filter the original signal using the bandpass filter bank. It is obvious that such a bandpass filter bank is difficult to be constructed. Fortunately, VMD provides a solution to the construction of the above stated bandpass filter bank whose optimization objection is based on variational analysis, and several intrinsic mode functions (IMFs) with narrow-band property could be obtained iteratively by VMD. Some VMD based methods have been proposed and used in fault diagnosis of rotating machinery [23-26]. However, fault diagnosis methods based on VMD require precise setting of the number of mode decomposition in advance. In addition, the VMD-based methods extract multiple modes simultaneously when there is only one target extraction mode, resulting in additional large computational costs. The later proposed VME method avoids the above-mentioned drawbacks of VMD effectively, which only extracts the target mode, thus having higher computational efficiency compared with VMD. The feature of VME is very suitable for extracting periodic impact components when rolling bearing fails. However, VME [9] still requires the center frequency of the target extracted components as one prior parameter. In addition, VME assumes that the extracted target components are concentrated within the frequency band centered on the prior center frequency. Therefore, it is highly likely to cause leakage of harmonic components of the target signal when VME is used for extracting periodic impact components. Choosing a larger bandwidth could avoid the leakage of harmonic components of the target signal, but it may cause higher noise pollution within the frequency band. To use the virtues of VME and retain the desired harmonics of the target extracted impulse components, a corresponding method named variational multi-harmonic mode function (VMHME) [27] is proposed. Furthermore, VMHME could remove the in-band noise. In fact, VMHME could be regarded as the aforementioned ideal bandpass filter bank in a certain sense. However, VMHME needs to estimate the fault characteristic frequency of test bearing accurately and use it as one prior input parameter. At present, the theoretical fault characteristic frequency of rolling bearings is commonly used as the estimated fault characteristic frequency. However, due to the installation deformation of rolling bearings and the random sliding between the rolling elements and the raceway during operation, it can cause a deviation between the actual fault characteristic frequency and the theoretical fault characteristic frequency. The most scientific and effective method is to enable VMHME to adaptively obtain the fault characteristic frequency based on the characteristics of the analyzed signal itself. Correspondingly, an AVMHME method is proposed in the paper, which could estimate the fault characteristic frequency of the analyzed signal correctly and adaptively based on EHPS. The main contributions of the paper are as follows: 1) An adaptive fault characteristic frequency estimation method based on EHPS is proposed. 2) The proposed fault characteristic frequency estimation method is introduced into VMHME and a corresponding AVMHME method is proposed and used in early weak fault feature extraction of rolling bearing. 3) Effectiveness of the proposed method is verified through simulations and experiment, and its advantage over the other related new methods is also compared.

The rest organizations of the paper are follows: section 1 and section 2 are dedicated to the theories of VMHME and AVMHME respectively. Besides, some simulations are also presented in Section 1 and Section 2. Section 3 is the early weak fault experiment of rolling bearing to verify effectiveness of the proposed method. Comparison study is presented in Section 4 and conclusion is given in Section 5.

2. Variational multi-harmonic mode extraction

The intrinsic mode function (IMF) is defined one single-component amplitude modulation or frequency modulation signal with narrow band-width, which could be obtained through time-frequency decomposition methods such as empirical mode decomposition (EMD), variational mode decomposition, variational mode extraction and so on. The $i t h$ IMF in the above time-frequency decomposition processes could be expressed as following equation:

1

u_{i} (t) = e_{i} (t) c o s (ϕ_{i} (t)),

where $e_{i} (t)$ represents one non-negative envelope function, and $ϕ_{i} (t)$ is the corresponding phase expression. The time-domain envelope of its impulse vibration signal exhibits broadband and multi harmonic characteristics, so the Eq. (1) is no longer applicable to describe the broadband and multi harmonic characteristics mentioned above [27]. The idea of multi-harmonic mode function (MHMF) is proposed, which not only could represent an ensemble of multi-harmonic components, but also have the property of broadband [27]. Besides, each harmonic in MHMF is narrow-band. The definition of MHMF is shown in Eq. (2):

2

m (t) = A_{0} + \sum_{k = 1}^{K} A_{k} (t) \cos (k w_{0} (t) t + θ_{k}),

in which $K$ represents the number of MHMF’ harmonics, $w_{0} (t)$ represents the wave’ instantaneous frequency, and the $k$ th harmonic’ initial phase is denoted by $θ_{k}$ . $A_{0}$ is average amplitude of the DC term.

VME only extracts the single target characteristic IMF, so it has higher efficiency than VMD. The concept of VMHME is proposed by the combination of virtues of VME with MHMF [27], and VMHME could extract the mode with explicit MHMF from the analyzed signal perfectly. Only two components (the desired MHHF $m (t)$ and the residual component $r (t)$ ) are supposed to be decomposed from the analyzed signal $g (t)$ , which could be expressed as following:

3

g (t) = m (t) + r (t),

4

m (t) = \sum_{k = 1}^{K} u_{k} (t) = \sum_{k = 1}^{K} A_{k} (t) \cos (k w_{0} (t) + θ_{k}),

in which the $k$ th harmonic in the MHMF is represented by $u_{k} (t)$ . The following two constraints are imposed on VMHME [27]:

1) Each harmonic in the MHMF should be narrowband, which means that each harmonic component should be distributed closely around its center frequency $k w_{0}$ in spite of that $m (t)$ is one broad-bandwidth component. Under the above constraint, the instantaneous frequency $w_{0} (t)$ could be replaced by the constant value $w_{0}$ , which is the mean frequency of $w_{0} (t)$ . So, $m (t)$ could be restricted by minimizing each harmonic’ bandwidth similar to VMD and VME, and the corresponding criterion is as following:

5

J_{1} = {\sum_{k = 1}^{K} ‖\partial_{t} [(δ (t) + \frac{j}{π t}) * u_{k} (t)] e^{- j k w_{0} t}‖}_{2}^{2} .

2) It should minimize the energy of the residual signal $r (t)$ as much as possible to obtain MHMF maximally. So, the following penalty function is constructed by using the squared $L^{2} - n o r m$ of $r (t)$ :

6

J_{2} = {‖r (t)‖}_{2}^{2} .

To sum up, the extraction of target MHMF could be restricted the following optimization problem:

7

\begin{array}{l} \underset{{u_{k} (t), {w_{0}}, r (t)}}{m i n} \{α J_{1} + J_{2}\}, \\ s . t . \sum_{k = 1}^{K} u_{k} (t) + r (t) = g (t), \end{array}

in which $α$ is the parameter balancing $J_{1}$ and $J_{2}$ , whose selection could be similar to VME.

The following constructed augmented Lagrangian combing one quadratic penalty term and Lagrangian multipliers is used to solve the reconstruction constraint of VMHME:

8

Γ (\{u_{k} (t)\}, \{w_{0}\}, \{r (t)\}, λ (t)) = α \sum_{k = 1}^{K} {‖\partial_{t} [(δ (t) + \frac{j}{π t}) * u_{k} (t)] e^{- j k w_{0} t}‖}_{2}^{2} + {‖r (t)‖}_{2}^{2} + β {‖g (t) - (\sum_{k = 1}^{K} u_{k} (t) + r (t))‖}_{2}^{2} + ⟨λ (t), g (t) - (\sum_{k = 1}^{K} u_{k} (t) + r (t))⟩,

in which $λ$ represents the Lagrangian multiplier, and $β$ represents the other set penalty parameter balancing the magnitude difference between the reconstruction error and the objective function. The ADMN [8] is used to solve the problem of Eq. (8). The variable $u_{k} (t)$ in VMHME should updated using following optimization objection function:

9

\begin{array}{l} u_{k}^{i + 1} = \underset{u_{k}}{a r g m i n} Γ (\{u_{j < k}^{i + 1}\}, \{u_{j \geq k}^{i}\}, \{w_{0}^{i}\}, \{r^{i}\}, λ^{i}) \\ = \underset{u_{k} \in X}{a r g m i n} α {‖\partial_{t} [(δ (t) + \frac{j}{π t}) * u_{k} (t)] e^{- j k w_{0} t}‖}_{2}^{2} \end{array}

+ β {‖g (t) - (\sum_{j} u_{j} (t) + r (t)) + \frac{λ (t)}{2 β}‖}_{2}^{2} .

Transform Eq. (9) into frequency domain as following for calculation simplification:

10

{\hat{u}}_{k}^{i + 1} = \underset{{\hat{u}}_{k} \in X}{a r g m i n} α {‖j (w - k w_{0}) [(1 + s g n (w)) {\hat{u}}_{(k)} (w)]‖}_{2}^{2}

+ β {‖\hat{g} (w) - (\sum_{j} {\hat{u}}_{j} (w) + \hat{r} (w)) + \frac{\hat{λ} (w)}{2 β}‖}_{2}^{2} .

The two composed parts in Eq. (10) could be further rewritten as following by using the real signal’ Hermite symmetry:

11

{\hat{u}}_{k}^{i + 1} = \underset{{\hat{u}}_{k} \in X}{a r g m i n} \{\int_{0}^{\infty} 4 α (w - k w_{0})^{2} {|{\hat{u}}_{k} (w)|}^{2} d w

+ 2 β \int_{0}^{\infty} {|\hat{g} (w) - (\sum_{j} {\hat{u}}_{j} (w) + \hat{r} (w)) + \frac{\hat{λ} (w)}{2 β}|}^{2} d w\} .

The final solution of ${\hat{u}}_{k}^{i + 1}$ is obtained as following:

12

{\hat{u}}_{k}^{i + 1} = \frac{\hat{g} (w) - (\sum_{j} {\hat{u}}_{j \neq k} (w) + \hat{r} (w)) + \frac{\hat{λ} (w)}{2 β}}{β + 2 α (w - k w_{0})^{2}} .

The solutions of $w_{0}$ and $\hat{r}$ could be obtained as follows similar to ${\hat{u}}_{k}$ :

13

\begin{array}{l} w_{0}^{i + 1} = \underset{w_{0}}{a r g m i n} Γ (\{u_{k}^{i + 1}\}, \{w_{0}^{i}\}, \{r^{i}\}, λ^{i}), \\ w_{0}^{i + 1} = \underset{w_{0}}{a r g m i n} \sum_{k} \int_{0}^{\infty} (w - k w_{0})^{2} {|{\hat{u}}_{k} (w)|}^{2} d w, \\ w_{0}^{i + 1} = \frac{\sum_{k} \int_{0}^{\infty} k w {|{\hat{u}}_{k} (w)|}^{2} d w}{\sum_{k} \int_{0}^{\infty} k^{2} {|{\hat{u}}_{k} (w)|}^{2} d w}, \\ r^{i + 1} = \underset{r}{a r g m i n} Γ (\{u_{k}^{i + 1}\}, \{r^{i}\}, λ^{i}), \\ {\hat{r}}^{i + 1} = \underset{\hat{r}}{a r g m i n} {\int_{0}^{\infty} |\hat{r} (w)|}^{2} d w + β \int_{0}^{\infty} |\hat{g} (w) - (\sum_{k} {\hat{u}}_{k} (w) + \hat{r} (w)) + \frac{\hat{λ} (w)}{2 β}|, \\ {\hat{r}}^{i + 1} = \frac{\hat{g} (w) - \sum_{k} {\hat{u}}_{k} (w) + \hat{λ} (w)}{1 + β} . \end{array}

The Lagrangian multiplier $λ$ is obtained by following equation:

14

{\hat{λ}}^{i + 1} = \hat{λ} + β (\hat{g} (w) - (\sum_{k} {\hat{u}}_{k} (w) + \hat{r} (w))) .

VMHME not only has the advantage of high computational efficiency same as VME, but also could extract the multi harmonic narrow band impulse signals effectively in the wide frequency range when fails arises in rolling bearing. However, VMHME needs to estimate the fault characteristic frequency of test bearing accurately and use it as one prior input parameter. The following two simulations are used to verify the above shortcomings of VMHME: the signal shown in Fig. 1(a) simulates the periodic impact characteristics ( $T =$ 0.1 s) that are interfered by other transient impact components with smaller amplitudes.

Fig. 1Simulation 1 verifying the shortcoming of VMHME

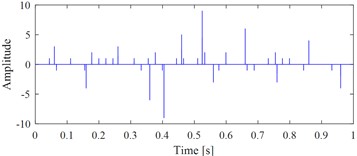
a) The original synthesized signal

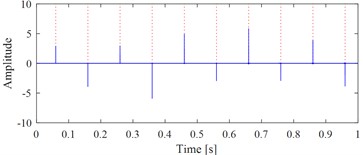
b) The extracted correct target signal using exact fault characteristic frequency

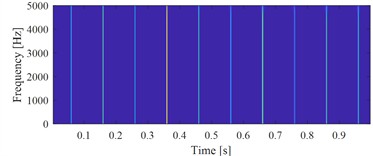
c) The time-frequency map of the signal shown in Fig. 1(b)

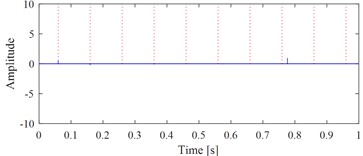
d) The extracted target signal using fault characteristic frequency with 1 % error

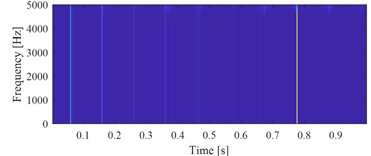
e) The time-frequency map of the signal shown in Fig. 1(d)

Fig. 2Simulation 2 verifying the shortcoming of VMHME

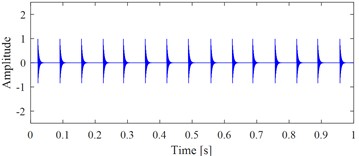
a) The target extracted signal

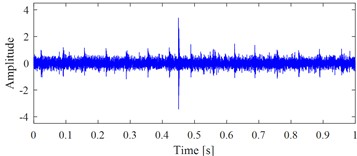
b) The signal shown in Fig. 2(a) with added noise

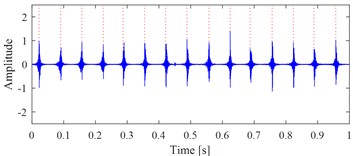
c) The extracted correct target signal using exact fault characteristic frequency

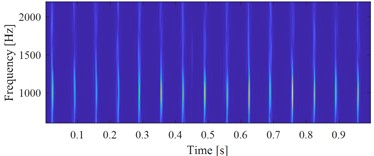
d) The time-frequency map of the signal shown in Fig. 2(c)

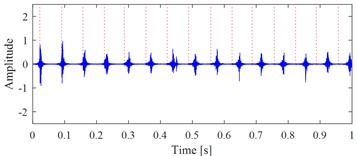
e) The extracted target signal using fault characteristic frequency with 1 % error

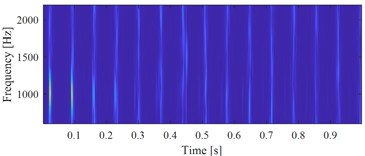
f) The time-frequency map of the signal shown in Fig. 2(e)

Fig. 1(b) and Fig. 1(c) show the correct extracted target signal and its time-frequency map by using the exact fault characteristic frequency as the input of VMHME, and Fig. 1(d) and Fig. 1(e) are the extracted target signal and its time-frequency map by using estimated fault characteristic frequency with 1 % error as the input of VMHME. The above stated shortcoming of VMHME could be observed intuitively based on Fig. 1. Fig. 2 shows the relevant simulation results to further verify the shortcoming of VMHME: Fig. 2(a) is an inner race fault simulation signal of rolling bearing, whose mathematical model could be referred to Eq. (17). Fig. 2(b) is the result by adding strong background noise into the signal as shown in Fig. 2(a). Fig. 2(c) is the extracted result of VMHME by using exact fault characteristic frequency, and Fig. 2(d) is the time-frequency map of the signal as shown in Fig. 2(c). Fig. 2(e) is the extracted result of VMHME by using fault characteristic frequency with 1 % error, and Fig. 2(f) is the time-frequency map of the signal as shown in Fig. 2(e).

3. Adaptive variational multi-harmonic mode extraction

Although the theoretical fault characteristic frequency calculation formulas of rolling bearing could calculate its fault characteristic frequencies effectively, installation errors and slight sliding between rolling bearing components during running could cause deviation between the actual fault characteristic frequency and the theoretical fault characteristic frequency. The most effective and scientific method is to estimate the fault characteristic frequency of test bearing according to the inherent characteristics of the analyzed signal itself. Autocorrelation function (AC) presented in equation (15) is the traditional and commonly used tool to estimate the exact period of the analyzed signal [28-29]. Unfortunately, it has been verified that effectiveness of AC will decrease under the strong inference of background noise [30]. It is well known that the envelope spectral result of faulty bearing’ vibration signal will take on harmonic-related spectral structure (HRSS), and the faulty type of test bearing could be reflected by the spectral interval of HRSS. The harmonic product spectrum (HPS) defined in Eq. (16) is a sensitive index for detecting the phenomenon of HRSS as verified in related reference [31]:

15

r_{x} (τ) \equiv \int x (t) x (t + τ) d τ,

16

H (w) = F (w) \cdot F (2 w) \cdot \dots \cdot F (M w) = \prod_{m = 1}^{M} F (m w),

in which $m$ and $F (w)$ represent the number of harmonics and the frequency amplitude of analyzed signal $x (t)$ respectively.

In this paper, apply envelope spectral analysis on the analyzed signal firstly. Subsequently, the HPS of the envelope result naming envelope HPS (EHPS) is analyzed to estimate the fault characteristic frequency of the analyzed signal: the frequency corresponding to the maximum amplitude in EHPS could be considered as the correct fault characteristic frequency [31].

The rolling bearing fault model whose mathematical equation can be expressed as Eq. (17) is used [32] to verify the feasibility of the proposed method. $τ_{i}$ is the tiny fluctuation around mean period $T$ . $n (t)$ represents the background noise. Set the sampling frequency $f_{s}$ = 16384 Hz, and the shaft rotation frequency is $f_{r}$ = 12 Hz. The inner race and outer race fault characteristic frequencies are $f_{i}$ = 47 Hz and. Set $f_{n}$ = 4000 Hz as the nature frequency of the system. Assuming the random slide between rolling element and race is normally distributed whose standard deviation is 0.5 % of the shaft rotation ratio, which causes the discrepancy between the theorical fault characteristic frequency and the actual fault characteristic frequency:

17

\{\begin{array}{l} x (t) = s (t) + n (t) = \sum_{i} A_{i} h (t - i T - τ_{i}) + n (t), \\ A_{i} = A_{0} c o s (2 π f_{r} t + ϕ_{A}) + C_{A}, \\ h (t) = e^{- B t} c o s (2 π f_{n} t + ϕ_{ω}) . \end{array}

Fig. 3(a) presents the inner race faulty signal of rolling bearing under the influence of strong background noise. Due to the influence of strong background noise, the periodic impulse characteristics in the time domain are obscured. Similarly, the corresponding envelope spectrum analysis result shown in Fig. 3(b) is also unable to extract the inner race fault characteristic frequency. In fact, the goal of VMHME is to extract as many harmonic components as possible, so the optimal estimated fault characteristic frequency should be corresponding to the largest number of harmonic components obtained by HRSS theoretically. The iteration for finding the optimal fault characteristic frequency of the analyzed signal should be terminated by HRSS when the number of harmonic components reaches largest. Fig. 3(c) shows the estimated fault characteristic frequency of signal shown in Fig. 3(a) corresponding to different number of harmonic components: the fault characteristic frequency of the target extracted component could be estimated correctly after 8 iterations. The estimated fault characteristic frequency value in Fig. 3(c) is used as input of VMHME, and the corresponding optimal final output is given in Fig. 3(d). The envelope spectrum of the last extracted signal shown in Fig. 3(d) is presented in Fig. 3(e), based on which the fault characteristic frequency with its harmonics is extracted successfully.

Fig. 3Simulation verifying the feasibility of AVMHME

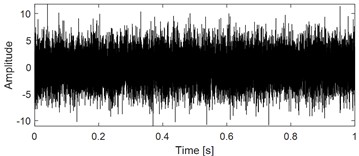
a) Rolling bearing simulation signal interfered with strong background noise

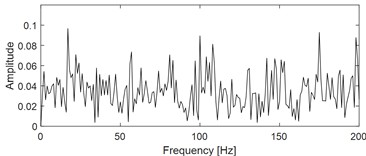
b) Envelope spectral of the signal as shown on Fig. 3(a)

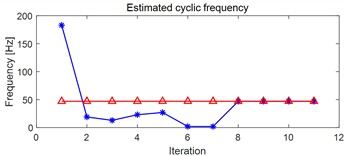
c) Estimated fault characteristic frequency based on EHPS

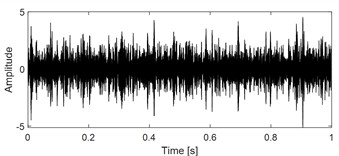
d) The extracted component based on VMHME using the estimated fault characteristic frequency as shown in Fig. 3(c)

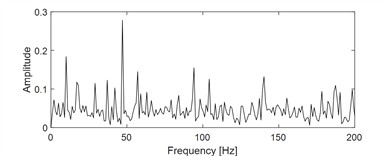
e) Envelope spectral of the signal as shown on Fig. 3(d)

4. Experiment

The ABLT-1A bearing test bench as shown in Fig. 4(a) is used for the accelerated life cycle test of rolling bearings. The test bench consists of a test head, a test head seat, a transmission system, a loading system, a lubrication system, an electrical control system, and a data acquisition system. This test bench can simultaneously install 4 bearings for accelerated fatigue life testing. The experiment adopts a strengthening test method to accelerate the failure rate of bearings in order to shorten the experimental period. The so-called strengthening test refers to loading an equivalent load (usually half of the rated dynamic load) higher than the reference load on the tested bearing without changing the contact fatigue failure mechanism of the rolling bearing. The loading schematic diagram is shown in Fig. 4(b).

Fig. 4The test bench and the schematic diagram of the radial loadings

a) The test bench

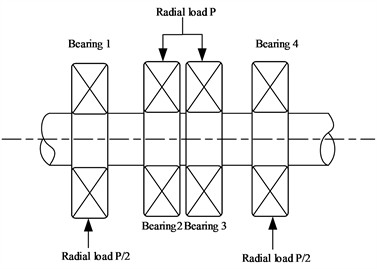
b) The schematic diagram of the loading

The test bearing used in this experiment is one kind of single row deep groove ball bearing with model 6307, and its structural parameters are shown in Table 1. The rotating frequency is 50 Hz and the corresponding theoretical fault characteristic frequencies of the test bearings are given in Table 2.

Table 1The parameters of the test rolling bearing

Type	Ball number	Ball diameter [mm]	Pitch diameter [mm]	Contact angle	Motor speed [rpm]	Load [kN]
6307	8	13.494	58.5	0	3000	12.744

Table 2The fault characteristic frequencies of the test rolling bearing

$f_{r}$	$f_{c}$	$f_{b}$	$f_{i}$	$f_{o}$
50 Hz	19 Hz	102 Hz	246 Hz	153 Hz

During the experiment, four rolling bearings were simultaneously installed on the test bench. Replace the bearing with a new one of the same model when one of the bearings experiences fatigue, and then continue the test until all bearings are tested. The first faulty bearing is used as the analysis object, as its full life data is least affected by interference from other bearings. Damage arises on the inner race of the first faulty bearing after the final disassembly. Collect one group of data every minute with the sampling frequency 25.6 kHz and sampling length 20480. The kurtosis index is a sensitive and effective indicator reflecting the early failure of rolling bearings. The kurtosis index curve of the analyzed bearing throughout its life cycle is shown in Fig. 5(a): the kurtosis index undergoes a sudden change at the 2297th minute, and the group data at the very moment could be regarded as the early fault step. Time domain waveform and envelope spectral corresponding the group data at 2297th minute are presented in Fig. 5(b) and (c) respectively. Due to the influence of strong background noise, not only the periodic impact characteristics of faulty bearing could not be reflected on the time-domain waveform, but also the inner race fault characteristic frequency with its harmonics could not be extracted based on Fig. 5(c).

The estimated cyclic frequency based on EHPS is given in Fig. 5(d), based on which though the estimated fault characteristic frequency approaches the theorical frequency, there are some little differences between them. Use the estimated fault characteristic frequency as the input of VMHME, and time domain waveform of the extracted components is presented in Fig. 5(e). Apply envelope spectral on the signal as shown in Fig. 5(e), and the corresponding result is shown in Fig. 5(f), based on which the inner race fault characteristic frequency and its harmonics are extracted perfectly.

Fig. 5Experiment verifying the effectiveness of the proposed AVMHME

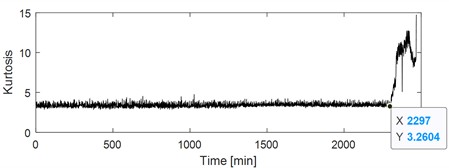
a) Kurtosis index curve over the faulty bearing’ life

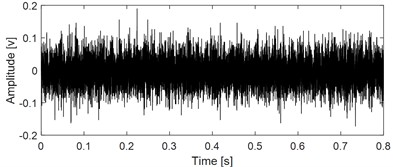
b) Time domain waveforms of the early weak fault step

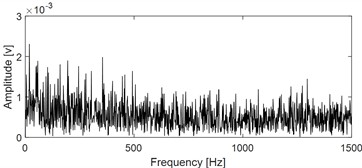
c) Envelope spectral of the signal shown in Fig. 5(b)

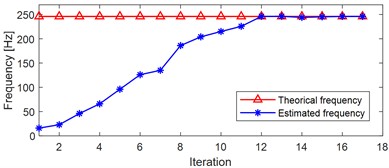
d) The estimated cyclic frequency by EHPS in the iteration process for the signal as shown in Fig. 5(b)

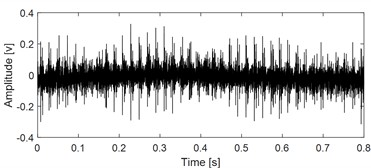
e) The extracted component as shown in Fig. 5(b) based on AVMHME

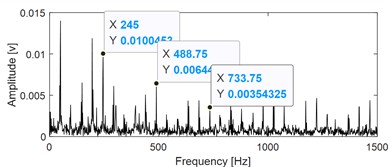
f) The envelope spectral of the signal as shown in Fig. 5(e)

Fig. 6 are the extraction results of the signal as shown in Fig. 5(b) based on VMHME: Fig. 6(a) is the time domain waveform of the extracted component and its corresponding envelope spectral result is given in Fig. 6(b). Though the inner race fault characteristic frequency 246 Hz could be extracted, its harmonic could not be extracted same as Fig. 5(f), which further verifies that small errors in estimating the fault characteristic frequency in VMHME calculation model will cause significant deviations in the target extraction components.

5. Comparison

The first method named as CFFsgram [33] is used for comparison, which is related to optimal resonance frequency band selection to obtain the best envelope effect. In CFFsgram, the original vibration of faulty bearing is filter by the constructed 1/3-binary tree filter bank to obtain series of narrowband signals. The candidate fault frequencies (CFFs) are identified by the local features of square envelope spectral of the obtained narrowband signals, and a CFFs-based indicator is designed to guide the selection of the optimal key parameters (center frequency and bandwidth). It is verified that CFFsgram has evident advantages over the other related methods. Apply CFFsgram analysis on the signal as shown in Fig. 5(b) and the results are shown in Fig. 7: Fig. 7(a) is the CFFsgram spectral, based on which the optimal key parameters are selected as: center frequency $f_{c} =$ 9200 Hz and $B_{w} =$ 267 Hz. Construct a band-pass filter using the two key parameters and filter the original signal as shown in Fig. 5(b), and time-domain waveform of the filtered component is given in Fig. 7(b) and its envelope spectral result is shown in Fig. 7(c). Unfortunately, the inner race fault characteristic frequency could not be identified based on Fig. 7(c).

Fig. 6The analysis results of the early weak fault of rolling bearing based on VMHME

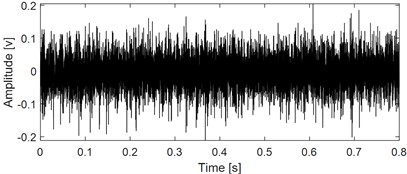
a) The extracted component as shown in Fig. 5(b) based on VMHME

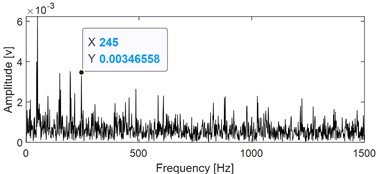
b) Envelope spectral of the signal as shown in Fig.6 (a)

Fig. 7Analysis results of the signal as shown in Fig. 5(b) based on CFFsgram

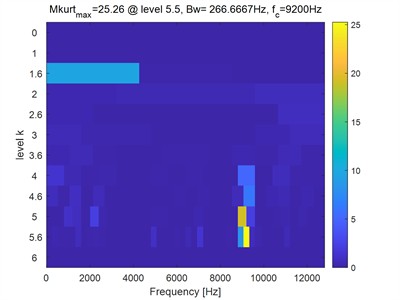
a) CFFsgram spectral of the signal as shown in Fig. 5(b)

b) Time domain waveform of the filtered signal using the band-pass filter based on the key parameters obtained by Fig. 7(a)

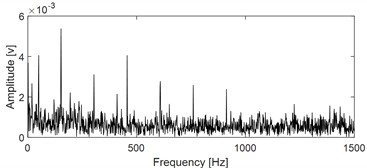
c) Envelope spectral of the signal as shown in Fig. 7(b)

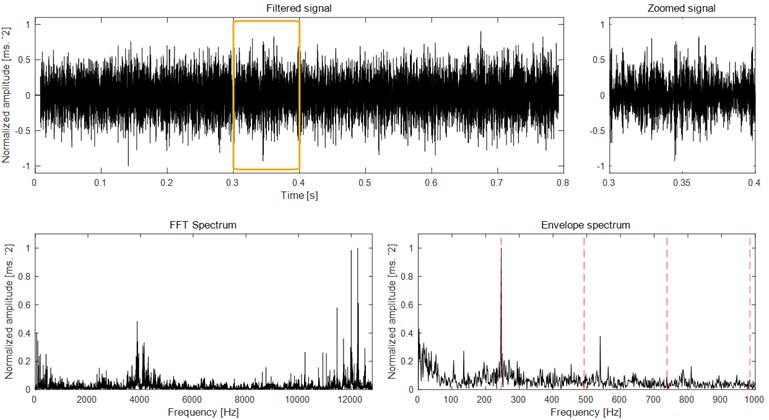
The second method used for comparison is minimum noise amplitude deconvolution (MNAD) [34], which is a new periodic weak impulse signal enhancement technology. A new index named periodic noise amplitude ratio is used by MNAD, which has advantages over the other popular blind deconvolution methods through verification. Fig. 8 shows the analysis results of the signal as shown in Fig. 5(b) based on MNAD: The impact characteristic of the filtered signal is enhanced evidently compared with the original signal as shown in Fig. 5(b), which is further verified by the zoomed signal. Though the envelope spectrum of the filtered signal extracts the inner race fault characteristic frequency, the harmonics of the inner race fault characteristic frequency are not extracted same as Fig. 5(f).

Fig. 8Analysis results of the signal as shown in Fig. 5(b) based on MNAD

6. Conclusions

The paper first verifies through simulations that the small error in the fault characteristic frequency, which is the key input parameter of VMHME will cause significant deviation in output. At present, VMHME takes the theoretical fault characteristic frequency of rolling bearing as the input parameter. Unfortunately, the deviation between the theoretical fault characteristic frequency and the actual fault characteristic frequency could not be avoided due to installation deformation and random sliding between the rolling elements and raceway during operation. To address the aforementioned issues, an AVMHME method is proposed in the paper, which could adaptively and accurately estimate the fault characteristic frequency of the analyzed signal based on EHPS. Then the estimated fault characteristic frequency is input into the VMHME model to obtain the final periodic multi harmonic impulse characteristic component. Effectiveness of the proposed AVMHME method is verified through early weak fault experiment on rolling bearing, and its superiority is also compared with the other two newer signal processing methods (one method is optimal response frequency band selection to maintain the best envelope effect and the other one is periodic weak impulse signal enhancement technology).

References

A. Rai and S. H. Upadhyay, “A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings,” Tribology International, Vol. 96, pp. 289–306, Apr. 2016, https://doi.org/10.1016/j.triboint.2015.12.037

Publisher
Q. Du and S. Yang, “Application of the EMD method in the vibration analysis of ball bearings,” Mechanical Systems and Signal Processing, Vol. 21, No. 6, pp. 2634–2644, Aug. 2007, https://doi.org/10.1016/j.ymssp.2007.01.006

Publisher
B. Liu, S. Riemenschneider, and Y. Xu, “Gearbox fault diagnosis using empirical mode decomposition and Hilbert spectrum,” Mechanical Systems and Signal Processing, Vol. 20, No. 3, pp. 718–734, Apr. 2006, https://doi.org/10.1016/j.ymssp.2005.02.003

Publisher
F. Wang, C. Liu, W. Su, Z. Xue, Q. Han, and H. Li, “Combined failure diagnosis of slewing bearings based on MCKD‐CEEMD‐ApEn,” Shock and Vibration, Vol. 2018, No. 1, p. 63217, Apr. 2018, https://doi.org/10.1155/2018/6321785

Publisher
M. A. Colominas, G. Schlotthauer, and M. E. Torres, “Improved complete ensemble EMD: a suitable tool for biomedical signal processing,” Biomedical Signal Processing and Control, Vol. 14, pp. 19–29, Nov. 2014, https://doi.org/10.1016/j.bspc.2014.06.009

Publisher
Y. Li, M. Xu, R. Wang, and W. Huang, “A fault diagnosis scheme for rolling bearing based on local mean decomposition and improved multiscale fuzzy entropy,” Journal of Sound and Vibration, Vol. 360, pp. 277–299, Jan. 2016, https://doi.org/10.1016/j.jsv.2015.09.016

Publisher
X. Zhang, C. Li, X. Wang, and H. Wu, “A novel fault diagnosis procedure based on improved symplectic geometry mode decomposition and optimized SVM,” Measurement, Vol. 173, p. 108644, Mar. 2021, https://doi.org/10.1016/j.measurement.2020.108644

Publisher
K. Dragomiretskiy and D. Zosso, “Variational mode decomposition,” IEEE Transactions on Signal Processing, Vol. 62, No. 3, pp. 531–544, Feb. 2014, https://doi.org/10.1109/tsp.2013.2288675

Publisher
M. Nazari and S. M. Sakhaei, “Variational mode extraction: a new efficient method to derive respiratory signals from ECG,” IEEE Journal of Biomedical and Health Informatics, Vol. 22, No. 4, pp. 1059–1067, Jul. 2018, https://doi.org/10.1109/jbhi.2017.2734074

Publisher
R. A. Wiggins, “Minimum entropy deconvolution,” Geoexploration, Vol. 16, No. 1-2, pp. 21–35, Apr. 1978, https://doi.org/10.1016/0016-7142(78)90005-4

Publisher
Y. Cheng, Z. Wang, W. Zhang, and G. Huang, “Particle swarm optimization algorithm to solve the deconvolution problem for rolling element bearing fault diagnosis,” ISA Transactions, Vol. 90, pp. 244–267, Jul. 2019, https://doi.org/10.1016/j.isatra.2019.01.012

Publisher
Y. Miao, J. Wang, B. Zhang, and H. Li, “Practical framework of Gini index in the application of machinery fault feature extraction,” Mechanical Systems and Signal Processing, Vol. 165, p. 108333, Feb. 2022, https://doi.org/10.1016/j.ymssp.2021.108333

Publisher
D. Zonoobi, A. A. Kassim, and Y. V. Venkatesh, “Gini index as sparsity measure for signal reconstruction from compressive samples,” IEEE Journal of Selected Topics in Signal Processing, Vol. 5, No. 5, pp. 927–932, Sep. 2011, https://doi.org/10.1109/jstsp.2011.2160711

Publisher
X. Jia, M. Zhao, Y. Di, P. Li, and J. Lee, “Sparse filtering with the generalized lp/lq norm and its applications to the condition monitoring of rotating machinery,” Mechanical Systems and Signal Processing, Vol. 102, pp. 198–213, Mar. 2018, https://doi.org/10.1016/j.ymssp.2017.09.018

Publisher
L. Li, “Sparsity-promoted blind deconvolution of ground-penetrating radar (GPR) data,” IEEE Geoscience and Remote Sensing Letters, Vol. 11, No. 8, pp. 1330–1334, Aug. 2014, https://doi.org/10.1109/lgrs.2013.2292955

Publisher
J. Antoni, “The spectral kurtosis: a useful tool for characterising non-stationary signals,” Mechanical Systems and Signal Processing, Vol. 20, No. 2, pp. 282–307, Feb. 2006, https://doi.org/10.1016/j.ymssp.2004.09.001

Publisher
J. Antoni and R. B. Randall, “The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines,” Mechanical Systems and Signal Processing, Vol. 20, No. 2, pp. 308–331, Feb. 2006, https://doi.org/10.1016/j.ymssp.2004.09.002

Publisher
J. Antoni, “Fast computation of the kurtogram for the detection of transient faults,” Mechanical Systems and Signal Processing, Vol. 21, No. 1, pp. 108–124, Jan. 2007, https://doi.org/10.1016/j.ymssp.2005.12.002

Publisher
T. Barszcz and A. Jabłoński, “A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kurtogram,” Mechanical Systems and Signal Processing, Vol. 25, No. 1, pp. 431–451, Jan. 2011, https://doi.org/10.1016/j.ymssp.2010.05.018

Publisher
J. Antoni, “The infogram: Entropic evidence of the signature of repetitive transients,” Mechanical Systems and Signal Processing, Vol. 74, pp. 73–94, Jun. 2016, https://doi.org/10.1016/j.ymssp.2015.04.034

Publisher
A. Moshrefzadeh and A. Fasana, “The Autogram: An effective approach for selecting the optimal demodulation band in rolling element bearings diagnosis,” Mechanical Systems and Signal Processing, Vol. 105, pp. 294–318, May 2018, https://doi.org/10.1016/j.ymssp.2017.12.009

Publisher
D. Peng, X. Zhu, W. Teng, and Y. Liu, “Use of generalized Gaussian cyclostationarity for blind deconvolution and its application to bearing fault diagnosis under non-Gaussian conditions,” Mechanical Systems and Signal Processing, Vol. 196, p. 110351, Aug. 2023, https://doi.org/10.1016/j.ymssp.2023.110351

Publisher
X. Zhang, Q. Miao, H. Zhang, and L. Wang, “A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery,” Mechanical Systems and Signal Processing, Vol. 108, pp. 58–72, Aug. 2018, https://doi.org/10.1016/j.ymssp.2017.11.029

Publisher
Y. Miao, M. Zhao, and J. Lin, “Identification of mechanical compound-fault based on the improved parameter-adaptive variational mode decomposition,” ISA Transactions, Vol. 84, pp. 82–95, Jan. 2019, https://doi.org/10.1016/j.isatra.2018.10.008

Publisher
J. Li, X. Cheng, Q. Li, and Z. Meng, “Adaptive energy-constrained variational mode decomposition based on spectrum segmentation and its application in fault detection of rolling bearing,” Signal Processing, Vol. 183, p. 108025, Jun. 2021, https://doi.org/10.1016/j.sigpro.2021.108025

Publisher
B. Pang, M. Nazari, and G. Tang, “Recursive variational mode extraction and its application in rolling bearing fault diagnosis,” Mechanical Systems and Signal Processing, Vol. 165, p. 108321, Feb. 2022, https://doi.org/10.1016/j.ymssp.2021.108321

Publisher
T. Jiang, Q. Zhang, X. Wei, and J. Zhang, “Variational multi-harmonic mode extraction for characterising impulse envelope of bearing failures,” ISA Transactions, Vol. 132, pp. 524–543, Jan. 2023, https://doi.org/10.1016/j.isatra.2022.05.042

Publisher
X. Xu, J. Lin, and C. Yan, “Adaptive determination of fundamental frequency for direct time-domain averaging,” Measurement, Vol. 124, pp. 351–358, Aug. 2018, https://doi.org/10.1016/j.measurement.2018.04.027

Publisher
Y. Miao, M. Zhao, J. Lin, and Y. Lei, “Application of an improved maximum correlated kurtosis deconvolution method for fault diagnosis of rolling element bearings,” Mechanical Systems and Signal Processing, Vol. 92, pp. 173–195, Aug. 2017, https://doi.org/10.1016/j.ymssp.2017.01.033

Publisher
C. Ding, M. Zhao, J. Lin, and J. Jiao, “Multi-objective iterative optimization algorithm based optimal wavelet filter selection for multi-fault diagnosis of rolling element bearings,” ISA Transactions, Vol. 88, pp. 199–215, May 2019, https://doi.org/10.1016/j.isatra.2018.12.010

Publisher
M. Zhao, J. Lin, Y. Miao, and X. Xu, “Detection and recovery of fault impulses via improved harmonic product spectrum and its application in defect size estimation of train bearings,” Measurement, Vol. 91, pp. 421–439, Sep. 2016, https://doi.org/10.1016/j.measurement.2016.05.068

Publisher
J. Antoni, F. Bonnardot, A. Raad, and M. El Badaoui, “Cyclostationary modelling of rotating machine vibration signals,” Mechanical Systems and Signal Processing, Vol. 18, No. 6, pp. 1285–1314, Nov. 2004, https://doi.org/10.1016/s0888-3270(03)00088-8

Publisher
N. Zhou, Y. Cheng, Z. Wang, B. Chen, and W. Zhang, “CFFsgram: A candidate fault frequencies-based optimal demodulation band selection method for axle-box bearing fault diagnosis,” Measurement, Vol. 207, p. 112368, Feb. 2023, https://doi.org/10.1016/j.measurement.2022.112368

Publisher
B. Fang, J. Hu, C. Yang, and X. Chen, “Minimum noise amplitude deconvolution and its application in repetitive impact detection,” Structural Health Monitoring, Vol. 22, No. 3, pp. 1807–1827, Aug. 2022, https://doi.org/10.1177/14759217221114527

Publisher

About this article

Received

08 August 2024

Accepted

24 December 2024

Published

22 January 2025

SUBJECTS

Fault diagnosis based on vibration signal analysis

DOI

https://doi.org/10.21595/jve.2024.24435

Keywords

variational multi-harmonic mode extraction

adaptive variational multi-harmonic mode extraction

envelope harmonic product spectrum

feature extraction

rolling bearing

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

Zhenhu Wang is the theoretical researcher and writer of the paper, and Chaozhong Liu is the program programmer in the paper.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Research article

2024 01 21

A gear fault diagnosis method based on variational mode decomposition and multi-scale discrete entropy

Tao Zhang, Yongqi Chen, Yang Chen, Qian Shen, Qinge Dai

Research article

2023 08 01

Motor rolling bearing fault diagnosis based on MVMD energy entropy and GWO-SVM

Jian Tang, Qiaoni Zhao

Research article

2022 08 23

Repetitive impacts recovering using variational mode extraction with constructed reference enhanced by improved blind deconvolution

Wenliao Du, Xukun Hou, Hongchao Wang

Research article

2021 11 05

Weak fault feature extraction of rolling element bearing based on variational mode extraction and multi-objective information fusion band-pass filter

Hongchao Wang, Wenliao Du, Haiyi Li, Zhiwei Li, Jiale Hu

Z. Wang and C. Liu, “Feature extraction of rolling bearing based on adaptive variational multi-harmonic mode extraction,” Journal of Vibroengineering, Vol. 27, No. 2, –14, Jan. 2025, https://doi.org/10.21595/jve.2024.24435

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2024.24435
UR  - https://doi.org/10.21595/jve.2024.24435
TI  - Feature extraction of rolling bearing based on adaptive variational multi-harmonic mode extraction
T2  - Journal of Vibroengineering
AU  - Wang, Zhenhu
AU  - Liu, Chaozhong
PY  - 2025
DA  - 2025/01/22
PB  - Extrica
VL  - 27
IS  - 2
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

 @article{Wang_2025, title={Feature extraction of rolling bearing based on adaptive variational multi-harmonic mode extraction}, ISSN={2538-8460}, url={https://doi.org/10.21595/jve.2024.24435}, DOI={10.21595/jve.2024.24435}, journal={Journal of Vibroengineering}, publisher={JVE International Ltd.}, author={Wang, Zhenhu and Liu, Chaozhong}, year={2025}, month=jan }

Copy Bibtex

Copied to clipboard!

[1]Z. Wang and C. Liu, “Feature extraction of rolling bearing based on adaptive variational multi-harmonic mode extraction,” Journal of Vibroengineering, Jan. 2025, doi: 10.21595/jve.2024.24435.

Copy IEEE

Copied to clipboard!

Wang, Zhenhu, and Chaozhong Liu. “Feature Extraction of Rolling Bearing Based on Adaptive Variational Multi-Harmonic Mode Extraction.” Journal of Vibroengineering, January 22, 2025. https://doi.org/10.21595/jve.2024.24435.

Copy Chicago

Copied to clipboard!

Feature extraction of rolling bearing based on adaptive variational multi-harmonic mode extraction

Abstract

1. Introduction

2. Variational multi-harmonic mode extraction

3. Adaptive variational multi-harmonic mode extraction

4. Experiment

5. Comparison

6. Conclusions

References

About this article

Related Articles