Abstract
This paper simulates the launching dynamics of the Terminal-guidance projectile considering the barrel thermo-chemical erosion wear and mechanical wear. A thermochemical erosive material degradation model that considers the rise in friction temperature is first introduced. Moreover, the wear state of barrel rifling at different periods is calculated using the erosion wear model. A three-dimensional model of the worn barrel is established, and the coupled barrel– terminal-guidance projectile launch dynamics are simulated for different wear periods. Finally, the projectile's bore overload and attitude are analyzed to explore the effect of barrel wear on launch.
Highlights
- A thermochemical erosive material degradation model that considers the rise in friction temperature is introduced.
- The erosive wear model is used to calculate the wear state of the barrel rifling at different times.
- The coupled barrel– terminal-guidance projectile launch dynamics are simulated and analyzed for different wear periods.
1. Introduction
Terminal-guidance projectile (TGP) can effectively enhance the suppression effect and destructive capability of artillery and have been emphasized by countries worldwide. As a guided projectile, the TGP faces many complex technical problems in order to meet the requirements of both precision guidance and artillery firing conditions. Of these, the most critical technical issue is the anti-overload technology. The process in the chamber of the TGP under artillery firing conditions is a complex nonlinear process characterized by high transient impact, intense load, high overload, large material deformation and damage failure, high-speed friction, and high temperature and pressure. This harsh environment places high shock and overload resistance requirements. The mechanism of ballistic processes in artillery varies somewhat at different barrel life cycles; the thermochemical erosion and mechanical wear accompanying artillery firing change the bore dimensions and, thus, the coupling law of the artillery [1, 2]. Relevant research on TGP overloading has been carried out [3-5], but research on the effect of bore erosion wear on the TGP has yet to be done. Exploring the launching dynamics mechanism of the TGP during the entire life cycle of the barrel is essential to improve the projectile’s operational reliability, system stability and control accuracy.
A thermochemical erosion material degradation model considering the friction temperature rise [6] can reasonably simulate the barrel's thermochemical erosion and mechanical wear behaviour during the projectile launching process. Therefore, based on the above erosion and wear model, this paper calculates the wear of barrel rifling under different life cycles and establishes the simulation models of the projectile-artillery coupled launch dynamics. By analyzing the projectile overload and attitude during different wear periods of the barrel, the effect of barrel wear on launching is summarized, which is of significant theoretical and practical significance for developing TGP.
2. Quantification of barrel bore erosion and wear
2.1. Model of erosion and wear
The barrel bore wear [6-9] is divided into two main categories: thermochemical erosion and the other is mechanical wear. One of the factors that cause thermochemical erosion of the barrel is mainly chemical erosion, thermal softening, thermal phase change, thermal melting, etc.; the factors that cause mechanical wear of the barrel are especially barrel-projectile friction movement, the impact of the projectile center band, and the scouring effect of the gunpowder gas flow. In the artillery firing process, the action mechanisms of erosion wear and mechanical wear are interrelated and work together to cause wear of the bore surface layer of the barrel. This paper uses a material degradation model for thermochemical erosion considering frictional temperature rise to describe the coupling relationship between thermochemical erosion and mechanical wear. Where the barrel bore thermochemical erosion [6] is represented by the following equation:
where h(t) is the thermal convection coefficient between the barrel chamber and high-temperature propellant gas, t0 and t1 are the start and end melting times of the artillery steel, T is the gunpowder gas temperature, Ts is the melting point of the barrel material, T0 is the initial ambient temperature, q1 is the heat flow distribution coefficient of the barrel material, q2 is the heat flow distribution coefficient of the rotating band material, Λ=0.53 is the projectile mass distribution coefficient, α is the rifling angle, S is the cross-sectional area of the barrel, μ is the frictional coefficient; p(x) is the base pressure of the projectile, which varies with the projectile stroke, ρ1 is the artillery steel density, c1 is the specific heat, r0 is the average width of the spiral rifling, L1 is the latent heat of artillery steel, l1 and l2 are the projectile strokes before and after the Δt.
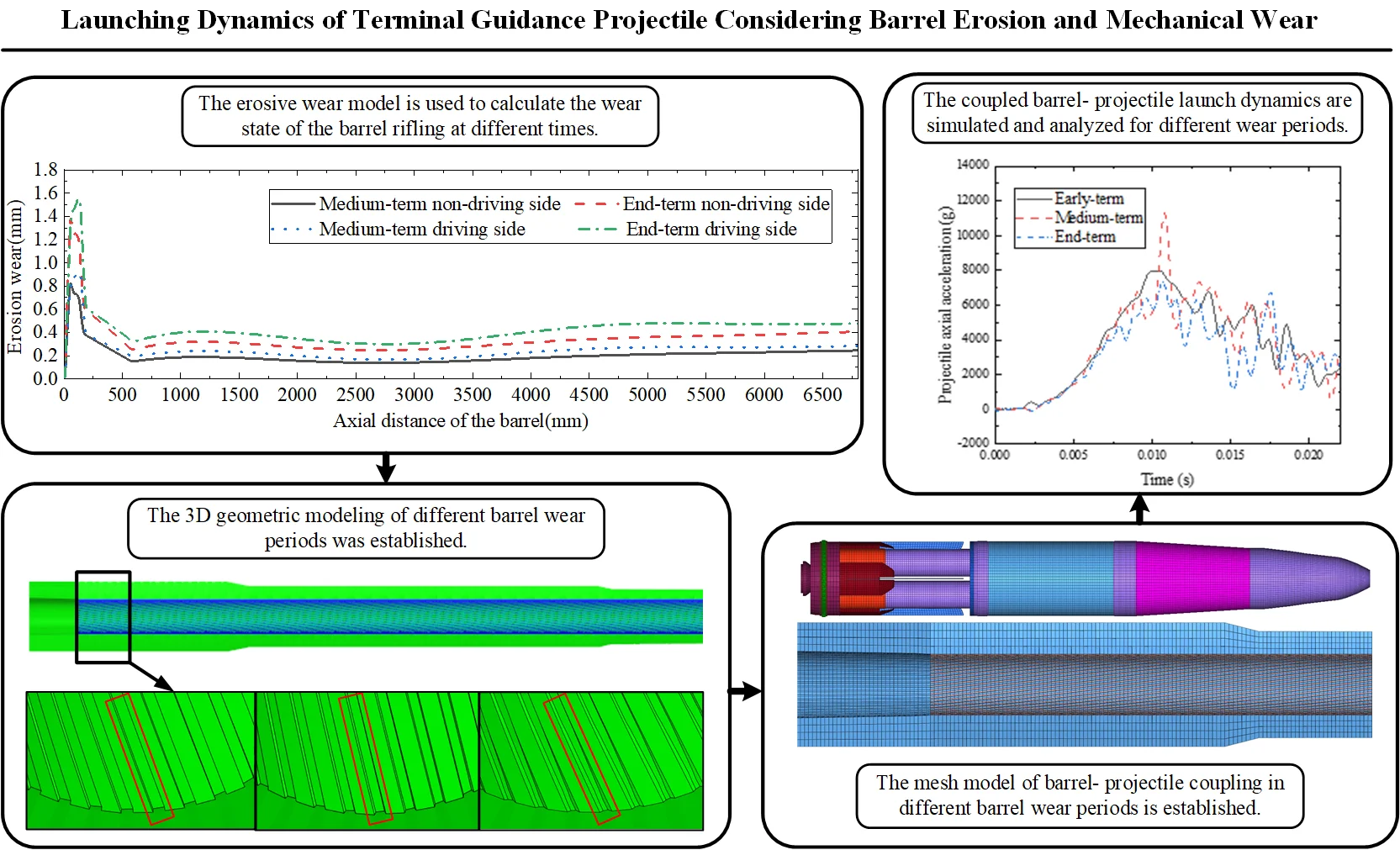
Fig. 1Schematic diagram of wear and modeling of the barrel at different periods
The following equation gives the mechanical wear [6] of the barrel’s inner bore:
where K= 6×10-4 is the mechanical wear rate of the copper/steel friction pair, s is the effective width of the rotating band, n is the projectiles number; Re=0.152 (μm) is the surface roughness, v is the projectile velocity, φ1 is the secondary work factor, m is the projectile mass, Rs is the mass eccentricity, η is the dynamic viscosity of molten metal, l is the projectile stroke.
Then the total wear is:
The wear of the barrel is calculated separately for different periods based on the above erosion wear model, where the early-term model assumes no wear, the middle-term model is for firing 300 projectiles, and the end-term model is for firing 500 projectiles. The upper part of Fig. 1 shows the results of numerical calculations of rifling wear along the axial direction of the barrel, and the lower part of Fig. 1 shows the modelling of the barrel for different wear periods.
2.2. Simulation modeling of launch dynamics
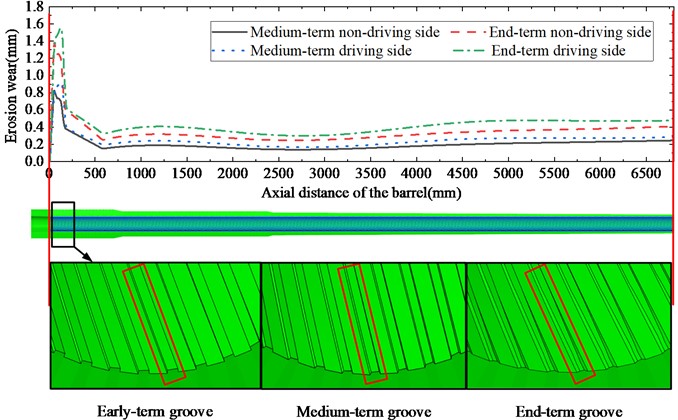
The projectile-gun coupling finite element discrete model is established based on the above barrel solid model in different periods and the TGP solid model. Among them, the barrel is divided by solid mesh, and the rifling wear geometric boundary strictly constrains the mesh shape to ensure the accurate establishment of the wear model [10]. The tail of the TGP is modelled using shell mesh, and the components such as the rotating band, sliding ring, guidance nose, control compartment, and warhead structure are all modelled by solid meshes. The projectile and barrel discretization is shown in Fig. 2.
Fig. 2Projectile-gun coupling finite element mesh
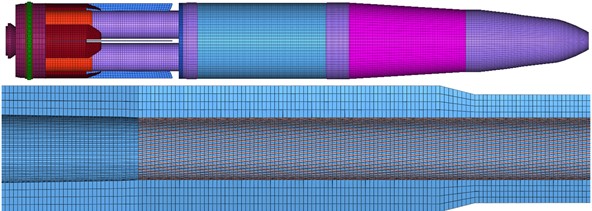
When the artillery is fired, the TGP is accelerated and spun in the rifled barrel. The loads applied in the coupled system are mainly gravity and base pressure. Gravity is realized by applying a vertically downward body force to the model. The base pressure is obtained by internal ballistic calculations considering the change in chamber volume and the closed gas drop by rifling wear, which is applied to the base of the TGP. The base pressure curves for different wear periods are shown in Fig. 3.
The end-guided projectile achieves in-bore de-spin using a sliding band, and contact relationships are set for sliding ring-sliding ring groove, band surface-barrel bore, and center band-barrel bore. The “hard contact” setup satisfies the impenetrability of the normal direction of the contacting objects, the prediction/correction algorithm imposes tangential friction constraints, and the collision contact forces are computed by the penalty function method [11].
Fig. 3Bore pressure curves for different wear periods
3. Calculation results and discussion
The launching dynamics of the TGP during different wear periods are simulated by using the above setup method and boundary conditions. The calculation results of the projectile in-bore overload for different wear periods of the barrel are shown in Fig. 4 and Fig. 5.
Fig. 4Different wear periods – projectile axial overloading
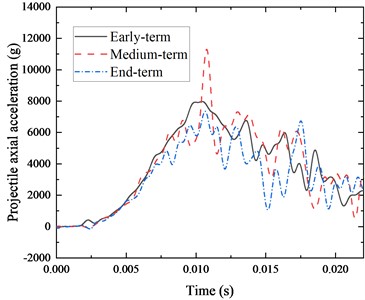
Fig. 5Different wear periods – projectile lateral overloading
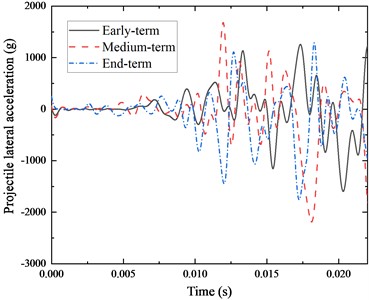
Table 1Overload peaks of TGP at different wear periods
Wear periods | Axial overload peak / 103g | Lateral overload peak / 103g |
Early-term | 7.975 | 1.593 |
Medium-term | 11.301 | –2.187 |
End-term | 7.354 | 1.757 |
From Fig. 4 and Table 1, it can be seen that the axial overload of the TGP varies significantly under different barrel wear conditions, with the minimum axial overload peak of 7.354×103 g, which occurs at the end-term and the maximum peak of 1.130×104 g, which occurs at the middle-term. The minor axial overload peak at the end is due to a more pronounced decrease in the base pressure as the barrel wears out, resulting in a decreasing trend throughout the end axial overload curve. It is clear, however, that there is a tendency for axial overload fluctuations to increase in the middle and end stages of internal ballistics as the barrel wears out.
From Fig. 5 and Table 1, it can be seen that the lateral overload peaks of the TGP also change significantly under different barrel wear conditions, with the maximum lateral peak of –2.187×103 g, which occurs in the middle-term and the minimum peak of 1.593×103 g, which occurs in the early-term. The lateral fluctuations of the projectile are also more intense in the middle and end terms than in the early term of wear.
The projectile in-bore vibration results for different wear periods of the barrel are shown in Fig. 6 to Fig. 7.
Fig. 6Different wear periods – projectile swing angle
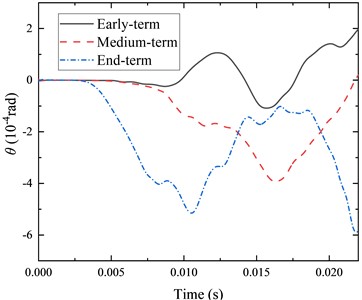
Fig. 7Different wear periods – projectile swing angular velocity
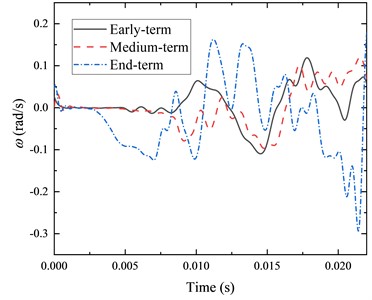
Table 2Swing angle and angular velocity of projectile at muzzle moment for different wear periods
Wear periods | θ (rad) | ω (rad/s) |
Early-term | 1.973e-4 | 0.0563 |
Medium-term | 0.196e-4 | 0.0686 |
End-term | –5.846e-4 | 0.177 |
Figs. 6, 7 and Table 2 show that the projectile swing angle and angular velocity change dramatically in different barrel wear cases. From Fig. 6, the increase in the gap between the projectile and the barrel due to the wear increases the peak of the projectile swing angle in the chamber, impacting the firing accuracy. From Fig. 7, with increased barrel wear, the bore boundary environment is not smooth, leading to increased fluctuations in the projectile swing angular velocity, which means that the projectile will be subjected to a more significant lateral overload, and the projectile electronic chip and guidance control equipment puts forward a higher overload resistance requirements.
4. Conclusions
The dynamic process of TGP launching is simulated in this paper for different wear periods. A thermochemical erosion material degradation model considering frictional temperature rise is used to calculate the wear of the barrel at different life cycles, and the 3D model of the worn barrel is established based on the calculation results. The projectile and artillery coupled firing dynamics are simulated for different wear periods, and the results show that with the increasing barrel wear, the radial and axial projectile overloads worsen, the swing angle peak gradually increases, and the swing angular velocity fluctuates more drastically. Barrel wear affects the projectile launching accuracy while placing higher demands on the projectile's resistance to overloading.
References
-
X.-L. Li, Y. Zang, Y. Lian, M.-Y. Ma, L. Mu, and Q. Qin, “An interface shear damage model of chromium coating/steel substrate under thermal erosion load,” Defence Technology, Vol. 17, No. 2, pp. 405–415, Apr. 2021, https://doi.org/10.1016/j.dt.2020.02.002
-
N. Rezgui, D. Mickovic, S. Zivkovicc, and I. Ivanovic, “Experimental and numerical analysis of thermo-chemical erosion in gun steel,” Thermal Science, Vol. 23, pp. 194–194, Jan. 2018, https://doi.org/10.2298/tsci180608194r
-
P. Verberne and S. A. Meguid, “Dynamics of precision guided projectile launch: solid-solid interaction,” International Journal of Structural Stability and Dynamics, Vol. 20, No. 14, p. 2043001, Sep. 2020, https://doi.org/10.1142/s0219455420430014
-
J. Li, C. Li, M. Jiang, and D. Zhou, “Mechanical analysis of failure of projectile-borne vibration sensor under high overload,” in Journal of Physics: Conference Series, Vol. 1168, p. 022015, Mar. 2019, https://doi.org/10.1088/1742-6596/1168/2/022015
-
X. W. Yin, P. Verberne, and S. A. Meguid, “Multiphysics modelling of the coupled behaviour of precision-guided projectiles subjected to intense shock loads,” International Journal of Mechanics and Materials in Design, Vol. 10, No. 4, pp. 439–450, May 2014, https://doi.org/10.1007/s10999-014-9255-0
-
S. Li, L. Wang, and G. Yang, “Unified computational model of thermochemical erosion and mechanical wear in artillery barrel considering hydrodynamic friction,” Numerical Heat Transfer, Part A: Applications, pp. 1–21, Oct. 2023, https://doi.org/10.1080/10407782.2023.2269604
-
S. Li, L. Wang, and G. Yang, “Surface damage evolution of artillery barrel under high-temperature erosion and high-speed impact,” Case Studies in Thermal Engineering, Vol. 42, p. 102762, Feb. 2023, https://doi.org/10.1016/j.csite.2023.102762
-
S. Li, L. Wang, F. Xu, and G. Yang, “Numerical simulations for artillery barrel temperature variation considering mechanical friction heat under continuous shots,” International Communications in Heat and Mass Transfer, Vol. 142, p. 106663, Mar. 2023, https://doi.org/10.1016/j.icheatmasstransfer.2023.106663
-
L. Wang, S. Li, F. Xu, and G. Yang, “United computational model for predicting thermochemical-mechanical erosion in artillery barrel considering friction behavior,” Case Studies in Thermal Engineering, Vol. 29, p. 101726, Jan. 2022, https://doi.org/10.1016/j.csite.2021.101726
-
C. Ding, N. Liu, and X. Zhang, “A mesh generation method for worn gun barrel and its application in projectile-barrel interaction analysis,” Finite Elements in Analysis and Design, Vol. 124, pp. 22–32, Feb. 2017, https://doi.org/10.1016/j.finel.2016.10.003
-
C. Y. Guo, G. L. Yang, J. L. Ge, and Q. Z. Sun, “Effect of ramming initial state on band engraving in smooth-bore guns,” Journal of Physics: Conference Series, Vol. 2478, No. 2, p. 022009, Jun. 2023, https://doi.org/10.1088/1742-6596/2478/2/022009
About this article
This research was financially supported by the “Jiangsu Province Natural Science Foundation” [Grant No. BK20210342], the “National Natural Science Foundation of China” [Grant No. 52105106].
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.

