Force analysis of the planetary-type mechanisms of the enhanced vibration exciters

Korendiy, Vitaliy; Parashchyn, Oleh; Stetsko, Andrew; Litvin, Roman; Kotsiumbas, Oleh; Pelo, Roman

doi:10.21595/vp.2024.24029

Vibroengineering Procedia

Browse Procedia

Published: 04 April 2024

Check for updates

Force analysis of the planetary-type mechanisms of the enhanced vibration exciters

Vitaliy Korendiy¹

Oleh Parashchyn²

Andrew Stetsko³

Roman Litvin⁴

Oleh Kotsiumbas⁵

Roman Pelo⁶

^{1, 2, 3}Department of Technical Mechanics and Engineering Graphics, Lviv Polytechnic National University, Lviv, Ukraine

^{4, 5, 6}Department of Motor Vehicle Transport, Lviv Polytechnic National University, Lviv, Ukraine

Corresponding Author:

Vitaliy Korendiy

Cite the article Download PDF

Downloads 38

Abstract

The planetary-type vibration exciters are relatively novel and prospective types of actuators for various vibratory technological equipment. Numerous research papers substantiated the possibilities of implementing such exciters for generating circular, elliptical, and rectilinear oscillations of the working members of different technological machines. The present research continues the authors’ previous investigations dedicated to kinematics and dynamics of planetary-type vibration exciters and is focused on the analysis of forces, moments, and torques acting upon the elements of the corresponding actuating mechanisms. The research methodology contains the development of the simplified dynamic diagrams of two different designs of planetary-type mechanisms, derivation of the analytical expressions describing force parameters of the considered mechanical systems, performing the mathematical modeling and computer simulation of the mechanism motion in order to analyze the corresponding forces, moments, and torques. The obtained results present the time dependencies of the mentioned force parameters under different operational conditions and design parameters of the planetary-type mechanism. The major scientific novelty of the paper consists in defining the minimal required torque of the motor needed to be applied for driving the mechanism at different conditions. The research outcomes can be effectively used by engineers while developing new and improving existent vibratory technological machines equipped with the considered planetary-type vibration exciter.

Force analysis of the planetary-type mechanisms of the enhanced vibration exciters

Highlights

Two planetary-type mechanisms with internal and external gearing used for actuating inertial vibration exciters of various vibratory technological equipment are considered.
The expressions describing their kinematic and force characteristics are deduced allowing for evaluating the reactions in the hinges and the moment of the forces acting upon the carrier.
The obtained results present the time dependencies of the mentioned force parameters under different operational conditions and design parameters of the planetary-type mechanism.

1. Introduction

Modern vibratory technological equipment uses various types of vibration exciters, which differ by design parameters and operation peculiarities. One of the simplest designs is based on the crank-type mechanism that actuates the reciprocating screen or sieve [1]. Another type of commonly used vibration exciters uses the centrifugal forces generated due to the rotation of the imbalanced shafts [2]. An interesting design of the twin crank-slider excitation mechanism is proposed in [3]. The possibilities of implementing multi-rotor systems with one active drive for actuating vibratory technological machines are thoroughly studied in [4] and [5]. Another prospective design of the inertial vibration exciter is based on the ball-type actuators [6]. The paper [7] considers the peculiarities of implementing the double-rotor exciters and nonlinear springs in vibratory systems. In [8], the authors study the dynamic behavior of the mobile robot equipped with the enhanced pantograph-type suspension and imbalanced rotor. The use of the crank-type exciter for actuating the vibratory screening conveyor is analyzed in [9].

The planetary-type vibration exciters are relatively novel and prospective types of actuators for various vibratory technological equipment. The possibilities of providing the time-varying operational characteristics of the planetary gears are comprehensively investigated in [10]. The influence of different dynamic parameters on the vibration response of these gears is considered in [11]. The paper [12] analyzes the main working regimes of the novel planetary-type vibration exciter. In [13], the authors study the dynamics of an enhanced adjustable planetary-type exciter driven by the chain gear. The modeling of torsional vibrations of the planetary gear train is performed in [14], where the corresponding frequency spectrum analysis is conducted.

The present research continues the authors’ previous investigations published in [15]-[17]. The generalized design of an asymmetric self-adjustable planetary-type vibration exciter was initially proposed in [15]. Further investigations were focused on the simplified symmetric design of the exciter allowing for generating the controllable circular, elliptical, and rectilinear trajectories of the single-mass oscillating systems [16]. The latest research results published in [17] were dedicated to kinematic analysis of the planetary-type mechanism that can be used as a vibration exciter of various vibratory technological machines. The present research is focused on the analysis of forces, moments, and torques acting upon the elements of the previously considered planetary-type mechanisms. Herewith, the major scientific novelty of the paper consists in defining the minimal required torque of the motor needed to be applied for driving the mechanism at different operational conditions and design parameters of the vibration exciter.

2. Research methodology

2.1. Dynamic diagrams of the planetary-type mechanisms of the enhanced vibration exciters

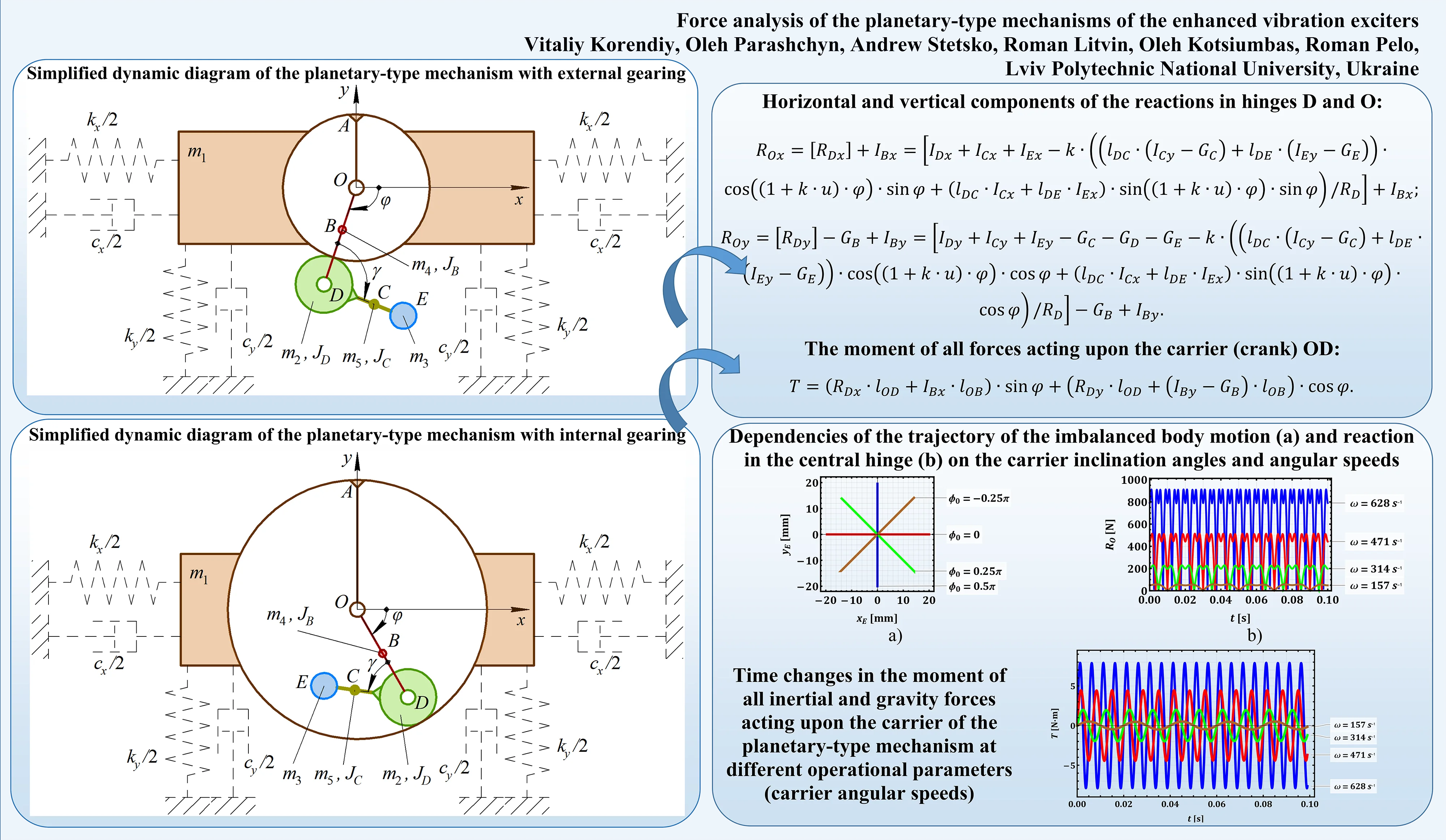
The simplified dynamic diagrams of the planetary-type mechanisms used for actuating vibration exciters are presented in Figs. 1 and 2. Considering the design with an external gearing (Fig. 1), when the planet gear rolls over the unmovable sun gear, the carrier $O D$ is set into rotary motion in a clockwise direction around the hinge $O$ . The latter is fixed on the machine’s working member and is chosen to be the origin of the inertial reference frame $x O y$ . The angular position of the carrier at an arbitrary moment of time is characterized by the angle $φ$ . Depending on the geometrical parameters of the mechanism, the angular position $γ$ of the planet gear $D$ and the imbalanced body $E$ can be unambiguously expressed in terms of the angle $φ$ . The inertial parameters of the considered mechanical system are characterized by the masses $m_{1}$ , $m_{2}$ , $m_{3}$ , $m_{4}$ , $m_{5}$ of the working member, planet gear, imbalanced body, carrier, and connecting rod, respectively. In addition, while performing further dynamic analysis, the moments of inertia of the corresponding bodies are considered relative to their centers of mass: $J_{B}$ , $J_{D}$ , $J_{C}$ .

Fig. 1Simplified dynamic diagram of the planetary-type mechanism with external gearing

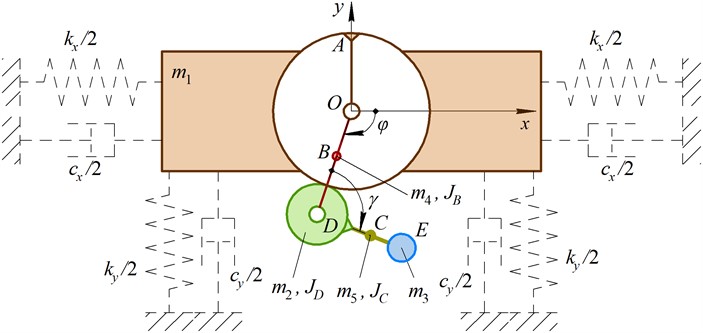
Similarly to the previously considered dynamic diagram, the mechanism with internal gearing (Fig. 2) is characterized by eight inertial parameters and two angles unambiguously defining the positions of all the movable elements in the inertial reference frame $x O y$ . The only distinction is the opposite direction of rotation of the planet gear caused by the clockwise rotation of the carrier. While performing further analysis, let us consider the case when the mechanisms’ geometrical and inertial parameters are prescribed, and the angle $φ$ is the known (pregiven) function of time $t$ . Particularly, the case of constant angular speed of the carrier $ω$ is to be studied.

Fig. 2Simplified dynamic diagram of the planetary-type mechanism with internal gearing

2.2. Analytical expressions defining kinematic and dynamic parameters of the mechanisms

According to the considered dynamic diagrams, the relation between the angles $γ$ and $φ$ , and the coordinates of the mass centers of the movable bodies can be expressed as follows:

1

φ = φ_{0} + ω ∙ t, γ = γ_{0} + ω ∙ (l_{O D} + R_{D}) / R_{D} ∙ t = γ_{0} + ω ∙ u ∙ t,

2

x_{B} = l_{O B} ∙ \cos φ, y_{B} = - l_{O B} ∙ \sin φ,

3

x_{D} = l_{O D} ∙ \cos φ, y_{D} = - l_{O D} ∙ \sin φ,

4

x_{C} = l_{O D} ∙ \cos φ - l_{D C} ∙ \cos (φ + k ∙ γ) = l_{O D} ∙ \cos φ - l_{D C} ∙ \cos ((1 + k ∙ u) ∙ φ),

5

y_{C} = l_{D C} ∙ \sin (φ + k ∙ γ) - l_{O D} ∙ \sin φ = l_{D C} ∙ \sin ((1 + k ∙ u) ∙ φ) - l_{O D} ∙ \sin φ,

6

x_{E} = l_{O D} ∙ \cos φ - l_{D E} ∙ \cos (φ + k ∙ γ) = l_{O D} ∙ \cos φ - l_{D E} ∙ \cos ((1 + k ∙ u) ∙ φ),

7

y_{E} = l_{D E} ∙ \sin (φ + k ∙ γ) - l_{O D} ∙ \sin φ = l_{D E} ∙ \sin ((1 + k ∙ u) ∙ φ) - l_{O D} ∙ \sin φ,

where $l_{O D}$ , $l_{O B}$ , $l_{D C}$ , $l_{D E}$ are the distances between the corresponding points; $R_{D}$ is the pitch radius of the planet gear; $k$ is the coefficient defining the type of the planetary-type mechanism: $k = 1$ for the mechanism with external gearing and $k =$ --1 for the mechanism with internal gearing; $u = (l_{O D} + R_{D}) / R_{D}$ is the substitution made for reducing the expressions length.

The horizontal and vertical components of speeds and accelerations of the corresponding mass centers can be derived as follows:

8

{\dot{x}}_{B} = - l_{O B} ∙ \dot{φ} ∙ \sin φ, {\dot{y}}_{B} = - l_{O B} ∙ \dot{φ} ∙ \cos φ,

9

{\dot{x}}_{D} = - l_{O D} ∙ \dot{φ} ∙ \sin φ, {\dot{y}}_{D} = - l_{O D} ∙ \dot{φ} ∙ \cos φ,

10

{\dot{x}}_{C} = (l_{D C} ∙ (1 + k ∙ u) ∙ \sin ((1 + k ∙ u) ∙ φ) - l_{O D} ∙ \sin φ) ∙ \dot{φ},

11

{\dot{y}}_{C} = (l_{D C} ∙ (1 + k ∙ u) ∙ \cos ((1 + k ∙ u) ∙ φ) - l_{O D} ∙ \cos φ) ∙ \dot{φ},

12

{\dot{x}}_{E} = (l_{D E} ∙ (1 + k ∙ u) ∙ \sin ((1 + k ∙ u) ∙ φ) - l_{O D} ∙ \sin φ) ∙ \dot{φ},

13

{\dot{y}}_{E} = (l_{D E} ∙ (1 + k ∙ u) ∙ \cos ((1 + k ∙ u) ∙ φ) - l_{O D} ∙ \cos φ) ∙ \dot{φ},

14

{\ddot{x}}_{B} = - l_{O B} ∙ ({\dot{φ}}^{2} ∙ \cos φ + \ddot{φ} ∙ \sin φ), {\ddot{y}}_{B} = l_{O B} ∙ ({\dot{φ}}^{2} ∙ \sin φ - \ddot{φ} ∙ \cos φ),

15

{\ddot{x}}_{D} = - l_{O D} ∙ ({\dot{φ}}^{2} ∙ \cos φ + \ddot{φ} ∙ \sin φ), {\ddot{y}}_{D} = l_{O D} ∙ ({\dot{φ}}^{2} ∙ \sin φ - \ddot{φ} ∙ \cos φ),

16

{\ddot{x}}_{C} = (l_{D C} ∙ {(1 + k ∙ u)}^{2} ∙ \cos ((1 + k ∙ u) ∙ φ) - l_{O D} ∙ \cos φ) ∙ {\dot{φ}}^{2} + (l_{D C} ∙ (1 + k ∙ u) ∙ \sin ((1 + k ∙ u) ∙ φ) - l_{O D} ∙ \sin φ) ∙ \ddot{φ},

17

{\ddot{y}}_{C} = (l_{D C} ∙ {(1 + k ∙ u)}^{2} ∙ \sin ((1 + k ∙ u) ∙ φ) + l_{O D} ∙ \sin φ) ∙ {\dot{φ}}^{2} + (l_{D C} ∙ (1 + k ∙ u) ∙ \cos ((1 + k ∙ u) ∙ φ) - l_{O D} ∙ \cos φ) ∙ \ddot{φ},

18

{\ddot{x}}_{E} = (l_{D E} ∙ {(1 + k ∙ u)}^{2} ∙ \cos ((1 + k ∙ u) ∙ φ) - l_{O D} ∙ \cos φ) ∙ {\dot{φ}}^{2} + (l_{D E} ∙ (1 + k ∙ u) ∙ \sin ((1 + k ∙ u) ∙ φ) - l_{O D} ∙ \sin φ) ∙ \ddot{φ},

19

{\ddot{y}}_{E} = (l_{D E} ∙ {(1 + k ∙ u)}^{2} ∙ \sin ((1 + k ∙ u) ∙ φ) + l_{O D} ∙ \sin φ) ∙ {\dot{φ}}^{2} + (l_{D E} ∙ (1 + k ∙ u) ∙ \cos ((1 + k ∙ u) ∙ φ) - l_{O D} ∙ \cos φ) ∙ \ddot{φ} .

The inertial and gravitational forces acting upon the mass centers are the following:

20

I_{B x} = - m_{4} ∙ {\ddot{x}}_{B}, I_{B y} = - m_{4} ∙ {\ddot{y}}_{B}, G_{B} = m_{4} ∙ g,

21

I_{D x} = - m_{2} ∙ {\ddot{x}}_{B}, I_{D y} = - m_{2} ∙ {\ddot{y}}_{B}, G_{D} = m_{2} ∙ g,

22

I_{C x} = - m_{5} ∙ {\ddot{x}}_{C}, I_{C y} = - m_{5} ∙ {\ddot{y}}_{C}, G_{C} = m_{5} ∙ g,

23

I_{E x} = - m_{3} ∙ {\ddot{x}}_{E}, I_{E y} = - m_{3} ∙ {\ddot{y}}_{E}, G_{E} = m_{3} ∙ g,

where $g$ is free-fall acceleration.

The horizontal and vertical components of the reactions in hinges $D$ and $O$ are equal to:

24

R_{O x} = [R_{D x}] + I_{B x} = [I_{D x} + I_{C x} + I_{E x} - k ∙ ((l_{D C} ∙ (I_{C y} - G_{C}) + l_{D E} ∙ (I_{E y} - G_{E})) ∙ \cos ((1 + k ∙ u) ∙ φ) ∙ \sin φ + (l_{D C} ∙ I_{C x} + l_{D E} ∙ I_{E x}) ∙ \sin ((1 + k ∙ u) ∙ φ) ∙ \sin φ) / R_{D}] + I_{B x},

25

R_{O y} = [R_{D y}] - G_{B} + I_{B y} = [I_{D y} + I_{C y} + I_{E y} - G_{C} - G_{D} - G_{E} - k ∙ ((l_{D C} ∙ (I_{C y} - G_{C}) + l_{D E} ∙ (I_{E y} - G_{E})) ∙ \cos ((1 + k ∙ u) ∙ φ) ∙ \cos φ + (l_{D C} ∙ I_{C x} + l_{D E} ∙ I_{E x}) ∙ \sin ((1 + k ∙ u) ∙ φ) ∙ \cos φ) / R_{D}] - G_{B} + I_{B y} .

The moment of all forces acting upon the carrier (crank) $O D$ gives the primary information about the torque of the motor needed to be applied in the hinge $O$ for actuating the mechanism:

26

T = (R_{D x} ∙ l_{O D} + I_{B x} ∙ l_{O B}) ∙ \sin φ + (R_{D y} ∙ l_{O D} + (I_{B y} - G_{B}) ∙ l_{O B}) ∙ \cos φ .

3. Results and discussion

3.1. Analyzing the reactions in the central hinges of the mechanisms

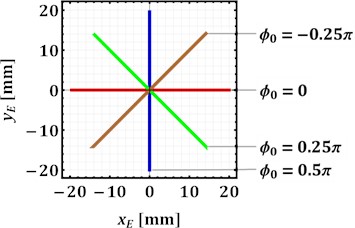
In order to perform further numerical modeling, let us consider the simplified case of the carrier uniform rotation at the constant angular speeds of $\dot{φ} =$ 157, 314, 471, 628 s^-1 (rotational frequencies of 25, 50, 75, 100 Hz), when the mass of the imbalanced body is equal to $m_{3} =$ 0.1 kg and its eccentricity is $l_{D E} =$ 0.01 m. Herewith, all the other inertial parameters of the system are neglected and assumed to be zero: $m_{2} = m_{4} = m_{5} =$ 0. The latter assumption can be proved when the vibration exciter is equipped with at least two symmetrically installed planet gears and synchronized imbalanced rotors. In addition, let us study three basic cases: 1) the imbalanced body describes a rectilinear trajectory in a vertical direction (e.g. while performing compacting processes); 2) in a horizontal direction (e.g., while conducting sieving processes); 3) in an inclined direction (e.g., while carrying out conveying processes). These three cases can take place when the geometrical parameters $R_{D}$ , $l_{D E}$ , and $l_{O D}$ are equal [17]: $R_{D} = l_{O D} = l_{D E} =$ 0.01 m. The corresponding trajectories can be generated at the following initial values of the angles $γ$ and $φ$ : 1) $φ_{0} = π / 2$ , $γ_{0} = π$ ; 2) $φ_{0} = 0$ , $γ_{0} = π$ ; 3) $φ_{0} = π / 4$ ( $φ_{0} = - π / 4$ ), $γ_{0} = π$ .

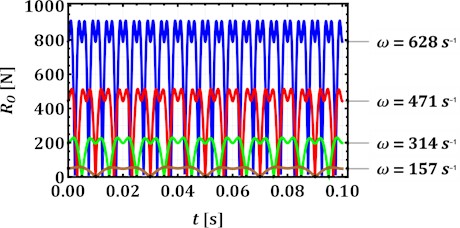
Considering the imbalanced body trajectories (Fig. 3(a)) simulated in the Mathematica software with the help of Eq. (6-7), while performing further investigations, let us analyze the first case when the imbalanced body describes a rectilinear trajectory in a vertical direction (e.g. while performing compacting processes). The corresponding time dependence characterizing the changes in the reaction of the central hinge $O$ $(R_{O} = \sqrt{R_{O x}^{2} + R_{O y}^{2}})$ of the mechanism with internal gearing at different angular speeds of the carrier is presented in Fig. 3(b). The lowest nominal values of the reaction of about 50 N are observed at the smallest angular speed of 157 s^–1 (25 Hz), while the highest values of the reactions reach 900 N at the forced frequency of 628 s^–1 (100 Hz).

Fig. 3Dependencies of the trajectory of the imbalanced body motion a) and reaction in the central hinge b) on the initial conditions (carrier inclination angles) and operational parameters (carrier angular speeds)

Dependencies of the trajectory of the imbalanced body motion a) and reaction in the central hinge b) on the initial conditions (carrier inclination angles) and operational parameters (carrier angular speeds)

a)

b)

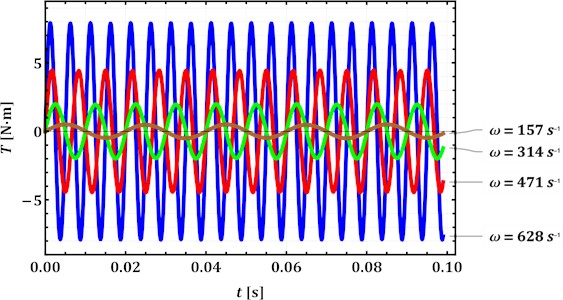
Fig. 4Time changes in the moment of all inertial and gravity forces acting upon the carrier of the planetary-type mechanism at different operational parameters (carrier angular speeds)

Time changes in the moment of all inertial and gravity forces acting upon the carrier of the planetary-type mechanism at different operational parameters (carrier angular speeds)

3.2. Analyzing the moment of all inertial and gravity forces acting upon the carrier

Considering the above-mentioned design and operational parameters of the planetary-type mechanism and the derived Eq. (26) of the moment of all forces acting upon the carrier, the corresponding time dependence is plotted in Fig. 4. The obtained simulation results show that the moment is a periodic function that changes in time at the twice larger frequency than the rotational frequency of the carrier. The maximal amplitude values of the moment of about 7 N∙m are reached at the forced frequency of 628 s^–1 (100 Hz), while the minimal ones of approximately 0.5 N∙m are observed at the lowest angular speed of the carrier of 157 s^–1 (25 Hz). The obtained data agree with the previous publications of the authors, e.g. [16], [17], and allow for primary evaluation of the necessary torque and power of the motor to be applied for actuating the excitation mechanism.

4. Conclusions

The paper considers two planetary-type mechanisms with internal and external gearing used for actuating inertial vibration exciters of various vibratory technological equipment. The corresponding dynamic diagrams are analyzed and the expressions describing their kinematic and force characteristics are deduced. The latter allow for evaluating the reactions in the hinges of the mechanisms and the moment of inertial and gravity forces acting upon the carrier. Considering the case of vertical rectilinear motion of the imbalanced body, the highest and lowest values of the reaction in the central hinge and the torque at the carrier are simulated: 50 N and 0.5 N∙m (at the carrier angular speed of 157 s^–1 (25 Hz)), 900 N and 7 N∙m (at 628 s^–1 (100 Hz)). Further research should be focused on experimental approval of the obtained simulation results.

References

H. Li, C. Liu, L. Shen, and L. Zhao, “Vibration characteristics of an industrial-scale flip-flow screen with crank-link structure and parameters optimization,” Shock and Vibration, Vol. 2021, pp. 1–16, Sep. 2021, https://doi.org/10.1155/2021/2612634

Publisher
N. Yaroshevich, O. Yaroshevych, and V. Lyshuk, “Drive dynamics of vibratory machines with inertia excitation,” Mechanisms and Machine Science, Vol. 95, pp. 37–47, Mar. 2021, https://doi.org/10.1007/978-3-030-60694-7_2

Publisher
V. Korendiy, V. Gursky, P. Krot, and O. Kachur, “Dynamic analysis of three-mass vibratory system with twin crank-slider excitation mechanism,” Vibrations in Physical Systems, Vol. 34, No. 2, pp. 2023226-1–2023226-9, Jan. 2023, https://doi.org/10.21008/j.0860-6897.2023.2.26

Publisher
V. Gurskyi, V. Korendiy, P. Krot, R. Zimroz, O. Kachur, and N. Maherus, “On the dynamics of an enhanced coaxial inertial exciter for vibratory machines,” Machines, Vol. 11, No. 1, p. 97, Jan. 2023, https://doi.org/10.3390/machines11010097

Publisher
W. Kang, P. Fang, Q. Yuan, Y. Hou, X. Jian, and H. Wang, “Synchronization and vibration absorption analysis of a dual-body vibrating screen driven by multiple motors with double-frequency actuation,” Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, pp. 1–19, Nov. 2023, https://doi.org/10.1177/09544062231200609

Publisher
V. Yatsun, G. Filimonikhin, I. Filimonikhina, and A. Haleeva, “Determining the energy efficiency of a resonance single-mass vibratory machine whose operation is based on the Sommerfeld effect,” Eastern-European Journal of Enterprise Technologies, Vol. 5, No. 7(113), pp. 44–51, Oct. 2021, https://doi.org/10.15587/1729-4061.2021.241950

Publisher
M. Du, Y. Hou, C. Yu, W. Wang, D. Hou, and G. Xiong, “Experimental investigation on synchronization of two co-rating rotors coupled with nonlinear springs,” IEEE Access, Vol. 8, pp. 48226–48240, Jan. 2020, https://doi.org/10.1109/access.2020.2975590

Publisher
V. Korendiy and O. Kachur, “Locomotion characteristics of a wheeled vibration-driven robot with an enhanced pantograph-type suspension,” Frontiers in Robotics and AI, Vol. 10, p. 1239137, Aug. 2023, https://doi.org/10.3389/frobt.2023.1239137

Publisher
O. Kachur and V. Korendiy, “Dynamic behavior of vibratory screening conveyor equipped with crank-type exciter,” in Lecture Notes in Mechanical Engineering, pp. 44–53, May 2023, https://doi.org/10.1007/978-3-031-32774-2_5

Publisher
Z. Xiao, J. Cao, and Y. Yu, “Mathematical modeling and dynamic analysis of planetary gears system with time-varying parameters,” Mathematical Problems in Engineering, Vol. 2020, pp. 1–9, Mar. 2020, https://doi.org/10.1155/2020/3185624

Publisher
Y. Liu, D. Zhen, H. Zhang, H. Zhang, Z. Shi, and F. Gu, “Vibration response of the planetary gears with a float sun gear and influences of the dynamic parameters,” Shock and Vibration, Vol. 2020, pp. 1–17, Aug. 2020, https://doi.org/10.1155/2020/8886066

Publisher
A. Kim, M. Doudkin, A. Ermilov, G. Kustarev, M. Sakimov, and M. Mlynczak, “Analysis of vibroexciters working process of the improved efficiency for ice breaking, construction and road machines,” Journal of Vibroengineering, Vol. 22, No. 3, pp. 465–485, May 2020, https://doi.org/10.21595/jve.2020.20446

Publisher
V. V. Mikheyev and S. V. Saveliev, “Planetary adjustable vibratory exciter with chain gear,” in Journal of Physics: Conference Series, Vol. 1210, No. 1, p. 012097, May 2019, https://doi.org/10.1088/1742-6596/1210/1/012097

Publisher
G. Huo et al., “Torsional vibration modelling of a two-stage closed differential planetary gear train,” in Mechanisms and Machine Science, Vol. 140, pp. 188–201, Aug. 2023, https://doi.org/10.1007/978-3-031-40459-7_13

Publisher
V. Korendiy, I. Kuzio, S. Nikipchuk, O. Kotsiumbas, and P. Dmyterko, “On the dynamic behavior of an asymmetric self-regulated planetary-type vibration exciter,” Vibroengineering Procedia, Vol. 42, pp. 7–13, May 2022, https://doi.org/10.21595/vp.2022.22580

Publisher
V. Korendiy, V. Gurey, V. Borovets, O. Kotsiumbas, and V. Lozynskyy, “Generating various motion paths of single-mass vibratory system equipped with symmetric planetary-type vibration exciter,” Vibroengineering Procedia, Vol. 43, pp. 7–13, Jun. 2022, https://doi.org/10.21595/vp.2022.22703

Publisher
V. Korendiy, O. Parashchyn, V. Heletiy, V. Pasika, V. Gurey, and N. Maherus, “Kinematic analysis and geometrical parameters justification of a planetary-type mechanism for actuating an inertial vibration exciter,” Vibroengineering Procedia, Vol. 52, pp. 35–41, Nov. 2023, https://doi.org/10.21595/vp.2023.23728

Publisher

About this article

Received

14 February 2024

Accepted

04 March 2024

Published

04 April 2024

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/vp.2024.24029

Keywords

vibratory technological equipment

force parameters

driving torque

operational conditions

design parameters

mathematical modeling

computer simulation

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 11 25

Kinematic analysis and geometrical parameters justification of a planetary-type mechanism for actuating an inertial vibration exciter

Vitaliy Korendiy, Oleh Parashchyn, Volodymyr Heletiy, Viacheslav Pasika, Volodymyr Gurey, Nadiia Maherus

Research article

2023 10 20

Generating rectilinear, elliptical, and circular oscillations of a single-mass vibratory system equipped with an enhanced twin crank-type exciter

Vitaliy Korendiy, Oleksandr Kachur, Rostyslav Predko, Oleh Kotsiumbas, Rostyslav Stotsko, Mykola Ostashuk

Research article

2022 12 12

Modelling and experimental investigation of the vibratory conveyor operating conditions

Vitaliy Korendiy, Oleksandr Kachur, Ihor Hurey, Rostyslav Predko, Roman Palash, Oleksandr Havrylchenko

Research article

2022 11 18

Experimental study of the lap motion trajectory of vibratory finishing machine

Vitaliy Korendiy, Oleksandr Kachur, Viktor Zakharov, Igor Kuzio, Ihor Hurey, Rostyslav Predko

V. Korendiy, O. Parashchyn, A. Stetsko, R. Litvin, O. Kotsiumbas, and R. Pelo, “Force analysis of the planetary-type mechanisms of the enhanced vibration exciters,” Vibroengineering Procedia, Vol. 54, pp. 28–34, Apr. 2024, https://doi.org/10.21595/vp.2024.24029

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2024.24029
UR  - https://doi.org/10.21595/vp.2024.24029
TI  - Force analysis of the planetary-type mechanisms of the enhanced vibration exciters
T2  - Vibroengineering Procedia
AU  - Korendiy, Vitaliy
AU  - Parashchyn, Oleh
AU  - Stetsko, Andrew
AU  - Litvin, Roman
AU  - Kotsiumbas, Oleh
AU  - Pelo, Roman
PY  - 2024
DA  - 2024/04/04
PB  - Extrica
SP  - 28-34
VL  - 54
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

 @article{Korendiy_2024, title={Force analysis of the planetary-type mechanisms of the enhanced vibration exciters}, volume={54}, ISSN={2538-8479}, url={https://doi.org/10.21595/vp.2024.24029}, DOI={10.21595/vp.2024.24029}, journal={Vibroengineering Procedia}, publisher={JVE International Ltd.}, author={Korendiy, Vitaliy and Parashchyn, Oleh and Stetsko, Andrew and Litvin, Roman and Kotsiumbas, Oleh and Pelo, Roman}, year={2024}, month=apr, pages={28–34} }

Copy Bibtex

Copied to clipboard!

[1]V. Korendiy, O. Parashchyn, A. Stetsko, R. Litvin, O. Kotsiumbas, and R. Pelo, “Force analysis of the planetary-type mechanisms of the enhanced vibration exciters,” Vibroengineering Procedia, vol. 54, pp. 28–34, Apr. 2024, doi: 10.21595/vp.2024.24029.

Copy IEEE

Copied to clipboard!

Korendiy, Vitaliy, Oleh Parashchyn, Andrew Stetsko, Roman Litvin, Oleh Kotsiumbas, and Roman Pelo. “Force Analysis of the Planetary-Type Mechanisms of the Enhanced Vibration Exciters.” Vibroengineering Procedia 54 (April 4, 2024): 28–34. https://doi.org/10.21595/vp.2024.24029.

Copy Chicago

Copied to clipboard!

Force analysis of the planetary-type mechanisms of the enhanced vibration exciters

Abstract

Highlights

1. Introduction

2. Research methodology

2.1. Dynamic diagrams of the planetary-type mechanisms of the enhanced vibration exciters

2.2. Analytical expressions defining kinematic and dynamic parameters of the mechanisms

3. Results and discussion

3.1. Analyzing the reactions in the central hinges of the mechanisms

3.2. Analyzing the moment of all inertial and gravity forces acting upon the carrier

4. Conclusions

References

About this article

Related Articles