Fourier series method for the stability solution of simply supported thin beams on two-parameter elastic foundations of the Pasternak, Filonenko-Borodich, Hetenyi or Vlasov models

1. Introduction

Foundation beams have been modeled using beam on elastic foundation theory that incorporates the reaction of the elastic foundation in the governing equation of beam theory to produce a governing differential equation for the foundation beam. The effect of the elastic foundation has been shown to affect the resulting behaviour of the foundation beam in buckling, bending or vibration.

Euler-Bernoulli beam theory (EBBT) has been commonly used for thin beams where the depth to span ratios are less than 0.05, while Timoshenko beam theory (TBT) and shear deformable beam theories of Dahake and Ghugal [1], Levinson [2] and Sayyad and Ghugal [3] have been used for thick beams where the depth to span ratios exceed 0.05. EBBT which assumes the Euler-Bernoulli Navier hypothesis of orthogonality of plane cross-sections to the longitudinal neutral axis before and after deformation disregards shear strains which are crucial in causing cross-sectional plane warping in beams. Hence, EBBT is suitable solely for thin beams, but produce unacceptable results for thick beams. EBBT equation is the fourth order ordinary differential equation in terms of the transverse deflection $u\left(x\right)$ and is given by Eq. (1):

for beam bending under distributed transverse load distribution, $q\left(x\right)$.

This work is focused on thin beams and hence used EBBT.

Elastic foundations have been modeled using discrete parameter and continuously distributed parameter models. Continuously distributed parameter models use the theory of elasticity to derive the reaction forces on the beams from the soil while discrete parameter models rely on the use of one, two or a limited number of parameters to describe the soil reaction pressures on the beam. Continuously distributed parameter models are difficult to formulate and use and are sparsely used. Discrete parameter foundation models are commonly used due to ease of formulation, simplicity in use and simplicity in the nature of the resulting governing equation.

Commonly used discrete parameter foundation models are (i) Winkler model, which is a one-parameter model, [4], [5], [6] (ii) two-parameter models derived by Pasternak, Vlasov, Hetenyi and Filonenko-Borodich amongst others [7], [8], [9] and (iii) three-parameter models due to Kerr [10], [11] which are rarely used.

The one-parameter Winkler model, which is illustrated in Figure 1, assumes the supporting soil to be a system of vertical, closely spaced, independent, linear elastic Hookean springs whose stiffness is directly proportional to the deflection. Hence, in the Winkler model, the soil reaction ($r\left(x\right)$) on the beam is directly proportional to the beam deflection ($u\left(x\right)$) at the point, where the proportionality constant is the Winkler constant, $k$, which is used to characterise the soil [4], [5], [6]. Thus, in the Winkler model, the equation for the reaction on the beam is given by Eq. (2):

The Winkler model fails to account for shear interaction of the springs and produces discontinuity issues.

Fig. 1Beam resting on a Winkler foundation model where the Winkler foundation model is a bed of closely speedy independent Hookean springs

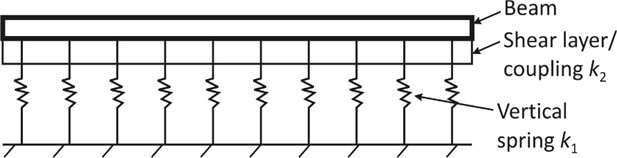
The two-parameter foundation model, which is typically illustrated in Fig. 2, utilizes two-parameters to derive the soil reaction, in an effort to overcome the limitations of the Winkler model in disregarding the shear interaction of the springs. The two-parameter models thus introduce another foundation parameter to account for the shear interaction between the closely spaced, linear elastic, vertical Hookean springs [7], [8], [9]. Hence, while the first parameter ($k_1$) represents the soil stiffness in the vertical direction, the second parameter ($k_2$) represents the coupling/shear interaction effect of the vertical Hookean springs. The reaction ($r\left(x\right)$) for the two-parameter models have been previously derived using equilibrium and variational calculus methods as expressed by Eq. (3):

Fig. 2Beam resting on a two-parameter foundation model where the two-parameter foundation model is graphically illustrated as a bed of closely spaced, linear elastic vertical Hookean springs with shear coupling present to model the shear interaction of the springs

Vlasov and Leontiev [12] adopted a simplified elastic continuum approach for the foundation and used the methods of variational calculus and energy minimization technique to derive the two-parameter Vlasov-Leontiev elastic foundation model. The Vlasov-Leontiev foundation model assumed the soil as an elastic layer and defined an arbitrary parameter ${\gamma }_1$ to characterize the vertical distribution of soil deformation.

Later, Jones and Xenophontos [13] developed an equation for the ${\gamma }_1$ parameter in terms of the displacement characteristics but did not provide any method for evaluating the ${\gamma }_1$ parameter. In another study, Vallabhan and Das [14], [15] determined the parameter ${\gamma }_1$ in terms of the beam and foundation soil characteristics using an iterative method and named the resulting model the modified Vlasov foundation.

Akhazhanov et al. [16] used the theory of elasticity to develop a simplified method for the analysis and solutions to beam on two-parameter elastic foundations. They validated their solution by comparison with solutions for beam on Winkler and Pasternak foundations and found that their solutions were identical with solutions based on Winkler and Pasternak foundation for various boundary conditions of the beam. Other contributions on beam on elastic foundations are in Akhazhanov et al. [17], [18], [19]; Huang et al. [20]. Akhmediev et al. [21] and Zhang et al. [22].

Gulkan and Alemdar [23] developed an analytical solution for the shape functions of a beam resting on a two-parameter elastic foundation. Their obtained solution is general and not restrictive to values of the foundation parameters. The exact shape function derived in their study is used to develop analytical expressions for the elements of the finite element stiffness matrices, nodal forces, mass and geometrical stiffness matrices.

Teodoru and Musat [24] also studied the finite element method of analysis of beam on linear variable two-parameter foundations. Olotu et al [25] used the semi-analytical approach called the differential transform method (DTM) to determine approximate solutions for the free vibration analysis of non-uniform beams resting on variable Winkler foundations. The elastic coefficients of the foundations were assumed to vary in the longitudinal dimensions of the beam. The DTM was applied to the equations of motion of the vibrating beam on variable Winkler foundation problem and the problem reduced to algebra. Computer codes implemented using MAPLE was used by Olotu et al. [25] to obtain solutions for clamped-clamped and simply supported boundaries, which were found to agree with previous solutions in the literature. Their works however did not consider buckling problems of beams on elastic foundation using DTM.

Aslami and Akimov [26] developed an efficient analytical method for the mathematical solution of continuous beams resting on two-parameter elastic foundations. The general form of their governing equation is reduced to a system of first order differential equations with constant coefficients; Jordan method in algebra is used to find the fundamental solution.

Beams on elastic foundations (BoEFs) subject to compressive forces can experience buckling failures, even when their material strengths have not been attained, when such compressive forces attain a certain critical value called the critical buckling load. It is thus vital for their design to have a critical buckling assessment performed in order to determine the critical buckling loads that would result in buckling failures.

Hetenyi [27], Timoshenko and Gere [28] and Wang et al. [29] have developed governing differential equations for stability (GDES) of beam on elastic foundation (BoEF) and derived analytical solutions for such GDES under various boundary conditions (simply supported, clamped-clampled, clamped-simply supported and clamped-free). In recent studies, Taha [30] and Taha and Hadima [31] used recursive differentiation method (RDM) for solving the GDES for BoEF and obtained analytical solutions for critical buckling loads for non-prismatic BoEF.

Soltani [32] solved the GDES for BoEF using the numerical approach of finite element analysis. Hassan [33] and Aristizabal-Ochoa [34] presented solutions for BoEF under different end supports. Anghel and Mares [35] solved the GDES for BoEF by using collocation techniques to solve the resulting integral formulation of the GDES. Atay and Coskun [36] used the variational iteration method (VIM) to solve the GDES for BoEF for prismatic and non-prismatic beams.

Ike [4] used the finite sine transformation method (FSTM) for the free vibration analysis of prismatic beam on Winkler foundations (BoWF) and obtained exact eigenvalues. Ike [5] used the generalized integral transform method (GITM) for free vibration analysis of the BoWF for various boundary conditions. Ike [6] presented a point collocation method (PCM) for the approximate solutions of the bending problem of BoWF and obtained acceptable results, which compared well with previous results in the literature. Ike et al. [37] used Picard’s iteration method for Euler buckling problems.

Ofondu et al. [38] used the Stodola-Vianello iteration method to solve Euler column buckling problems with clamped-pinned supports. Ikwueze et al. [39] used least squares weighted residual technique for the critical buckling load solutions of Euler columns with fixed-pinned ends. Mama et al. [40] used quintic polynomials as shape functions in a finite element analysis for the accurate buckling load solutions of BoWFs.

Ike et al [41] and Ike [42] used the Stodola-Vianello interaction method (SVIM) and polynomial shape function to find critical buckling load solutions of BoWF under clamped-clamped and simple end supports, respectively. Ike [43] applied the SVIM and exact trigonometric shape functions of simply supported beams to find exact critical buckling load solutions of BoWF for Dirichlet boundary conditions. Ike [7] implemented SVIM and exact trigonometric shape functions of Dirichlet boundary conditions to obtain exact eigenvalues for the eigenvalue problem of thin beam on Pasternak foundation. Ike et al. [8] and Ike [9] also implemented SVIM for Bo2PF using polynomial basis functions for clamped-clamped and simply supported boundaries, respectively.

Hariz et al. [44] investigated the buckling analysis of Timoshenko beam resting on two-parameter elastic foundations. Yue [45] used a refined beam model to study the behaviour of beams rested on two-parameter foundations by iterative method. Akgoz et al [46] studied the flexural analysis of beams on elastic foundations using the method of discrete singular convolution, but did not study buckling analysis.

Finite element methods were used in the studies of beam on elastic foundation by Alzubaidi et al. [47], Wieckowski and Swiatkiewiez [48], and Worku and Habte [49]. Theory of elasticity methods were also studied by Gholami and Alizadeh [50], Anyaegbunam [51] and Thanh and Linh [52]; but none studied buckling problems.

This work presents rigorous first principles derivation of the governing differential equations of elastic stability (GDES) for thin beams resting on two-parameter elastic foundations (Bo2PFs). The elastic foundations are modeled using Pasternak, Filonenko-Borodich, Hetenyi or Vlasov models using two-parameters, $k_1$ and $k_2$ while the slender beam is modeled using Euler-Bernoulli thin beam theory.

In this study, the Fourier series method (FSM) is adopted to obtain analytical solutions to simply supported thin beam resting on two-parameter foundations of the Pasternak, Hetenyi, Vlasov or Filonenko-Borodich type. The FSM is adopted due to its previously acclaimed success in dealing with ordinary differential equations (ODEs) and partial differential equations (PDEs) with Dirichlet boundary conditions and due to its effectiveness as a mathematical tool in obtaining analytical solutions to boundary value problems (BVPs).

2. Novelty of the study

The novelty of the study is the first principles, systematic derivation of the GDES of the Bo2PF problem under axial compression load; and the systematic application of the FSM to the solution of the GDES for Dirichlet boundary conditions.

2.1. Governing differential equation of stability (GDES)

2.1.1. The thin beam on two-parameter foundation

Fig. 3 shows the thin beam resting on two-parameter elastic foundation which is considered in this study.

Fig. 3Thin beam resting on two-parameter elastic foundation

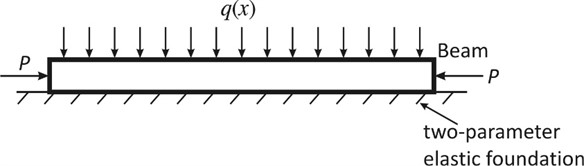
Fig. 3 shows that the thin beam has a finite span and is subjected to axial compressive force $P$ and transverse distributed load $q\left(x\right)$. The beam is simply supported at the ends $x=$0, $x=l$ where $l$ is the length of the beam.

2.1.2. Theoretical framework and assumptions

The assumptions of the formulation are as follows:

(i) The beam material is linearly elastic, homogeneous and isotropic.

(ii) The soil is linearly elastic, homogeneous and isotropic.

(iii) The displacements of the beam are very small relative to the thickness.

(iv) The axial strains are small as compared to unity.

(v) The normal strains in the transverse directions are so small and are considered insignificant.

(vi) The transverse shear stresses are also very small and negligible.

(vii) The cross-sections are plane and orthogonal to the longitudinal axis of the beam before and after flexural deformations.

2.2. Equations of equilibrium (EoE) for the elastic stability problem of Bo2PF

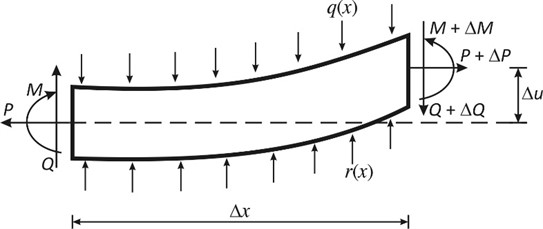
The free body diagram of an infinitesimal segment of the thin beam resting on two-parameter elastic foundation problem as considered in this paper is shown in Fig. 4.

In Fig. 4, P denotes the axial internal force at the left cut section; $P+\mathrm{\Delta }P$ is the axial internal force at the right cut section. $M$ is the bending moment acting at the left section, $M+\mathrm{\Delta }M$ is the bending moment acting at the right section; $q\left(x\right)$ is the distributed transverse loading intensity, $r\left(x\right)$ is the reaction from the two-parameter foundation on the beam. The deflection of the beam within the infinitesimal length $∆x$ is denoted by $∆u$. The elemental section of the thin beam on two-parameter elastic foundation is in equilibrium under the forces and reactions.

Fig. 4Free body diagram of an elemental segment of a thin beam resting on a two-parameter elastic foundation under compressive force

For translational equilibrium in the axial ($x$) direction:

4

$\sum F_{ix}=0.$

If forces in the positive $x$ direction are assumed to be positive, the translational equilibrium equation becomes:

5

$-P+(P+\mathrm{\Delta }P)=0.$

Solving:

6

$\mathrm{\Delta }P=0.$

Hence, axial force, $P$ is constant.

For translational equilibrium in the vertical direction:

7

$\sum F_y=0.$

If downward forces are positive, then:

8

$-Q+(Q+\mathrm{\Delta }Q)+q\left(x\right)\mathrm{\Delta }x-r\left(x\right)\mathrm{\Delta }x=0.$

Simplifying:

9

$\mathrm{\Delta }Q+\left(q\right(x)-r(x\left)\right)\mathrm{\Delta }x=0.$

Dividing by $∆x$ gives:

10

$\frac{\mathrm{\Delta }Q}{\mathrm{\Delta }x}+q\left(x\right)-r\left(x\right)=0.$

In the limit as $\mathrm{\Delta }x\to 0$:

11

$\frac{dQ}{dx}=\underset{\mathrm{\Delta }x\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{\mathrm{\Delta }Q}{\mathrm{\Delta }x}=r\left(x\right)-q\left(x\right).$

For rotational equilibrium about the left section, where anticlockwise moments are assumed as positive:

12

$\sum M_i=0.$

If anticlockwise moments are positive, the rotational equilibrium equation is:

13

$M+\mathrm{\Delta }M-M-(P+\mathrm{\Delta }P)\mathrm{\Delta }u-(Q+\mathrm{\Delta }Q)\mathrm{\Delta }x-q\left(x\right)\frac{\mathrm{\Delta }x\mathrm{\Delta }x}{2}+r\left(x\right)\mathrm{\Delta }x\frac{\mathrm{\Delta }x}{2}=0.$

Simplifying, Eq. (13) gives:

14

$\mathrm{\Delta }M-P\mathrm{\Delta }u-\mathrm{\Delta }P\mathrm{\Delta }u-Q\mathrm{\Delta }x-\mathrm{\Delta }Q\mathrm{\Delta }x-q\left(x\right)\frac{(\mathrm{\Delta }x{)}^2}{2}+r\left(x\right)\frac{(\mathrm{\Delta }x{)}^2}{2}=0.$

Further simplification of Eq. (14) gives, from Eq. (6), the following:

15

$\mathrm{\Delta }M-P\mathrm{\Delta }u-Q\mathrm{\Delta }x-\mathrm{\Delta }Q\mathrm{\Delta }x-q\left(x\right)\frac{(\mathrm{\Delta }x{)}^2}{2}+r\left(x\right)\frac{(\mathrm{\Delta }x{)}^2}{2}=0,$

since $\mathrm{\Delta }P=0$.

Dividing Eq. (15) by $∆x$ gives:

16

$\frac{\mathrm{\Delta }M\left(x\right)}{\mathrm{\Delta }x}-P\frac{\mathrm{\Delta }u\left(x\right)}{\mathrm{\Delta }x}-Q-\mathrm{\Delta }Q-q\left(x\right)\frac{\mathrm{\Delta }x}{2}+r\left(x\right)\frac{\mathrm{\Delta }x}{2}=0.$

In the limit as elemental quantities tend to zero, $\mathrm{\Delta }x\to 0$, $\mathrm{\Delta }Q\to 0$ and:

17

$\mathrm{l}\mathrm{i}\mathrm{m}\left(\frac{\mathrm{\Delta }M\left(x\right)}{\mathrm{\Delta }x}-P\frac{\mathrm{\Delta }u}{\mathrm{\Delta }x}-Q-\mathrm{\Delta }Q-q\left(x\right)\frac{\mathrm{\Delta }x}{2}+r\left(x\right)\frac{\mathrm{\Delta }x}{2}\right)=0.$

Hence:

18

$\frac{dM\left(x\right)}{dx}-P\frac{du\left(x\right)}{dx}-Q=0.$

Differentiating Eq. (18) with respect to $x$ gives:

19

$\frac{d}{dx}\left(\frac{dM}{dx}-P\frac{du}{dx}-Q\right)=0.$

Hence:

20

$\frac{d^{2}M\left(x\right)}{d{x}^2}-P\frac{d^{2}u\left(x\right)}{d{x}^2}-\frac{dQ}{dx}=0.$

Substitution of Eq. (11) into Eq. (20) gives:

21

$\frac{d^{2}M\left(x\right)}{d{x}^2}-P\frac{d^{2}u\left(x\right)}{d{x}^2}=\frac{dQ}{dx}=r\left(x\right)-q\left(x\right).$

Hence:

22

$\frac{d^{2}M\left(x\right)}{d{x}^2}-P\frac{d^{2}u\left(x\right)}{d{x}^2}=r\left(x\right)-q\left(x\right).$

The moment deflection equation of Euler-Bernoulli beam theory is:

23

$M\left(x\right)=-EI{u}^{\text{'}\text{'}}\left(x\right)=-EI\frac{d^{2}u\left(x\right)}{d{x}^2}.$

Hence, the equation of equilibrium is:

24

$\frac{d^2}{d{x}^2}\left(-EI\frac{d^{2}u\left(x\right)}{d{x}^2}\right)-P\frac{d^{2}u\left(x\right)}{d{x}^2}=r\left(x\right)-q\left(x\right).$

The governing equation for the stability of thin prismatic beam on elastic foundations is given from equilibrium conditions as:

25

$EI{u}^{iv}\left(x\right)+P{u}^{\text{'}\text{'}}\left(x\right)=q\left(x\right)-r\left(x\right),$

where the primes denote differentiations with respect to the space variable, $x$.

By substitution of the expression for $r\left(x\right)$ as given for two-parameter foundations by Eq. (2), the governing equation becomes:

26

$EI{u}^{iv}\left(x\right)+P{u}^{\text{'}\text{'}}=q\left(x\right)-\left(k_{1}u\left(x\right)-k_2{u}^{\text{'}\text{'}}\left(x\right)\right).$

Hence, simplifying gives:

27

$EI{u}^{iv}+P{u}^{\text{'}\text{'}}\left(x\right)+k_{1}u\left(x\right)-k_2{u}^{\text{'}\text{'}}\left(x\right)=q\left(x\right).$

Hence, the governing equation is written explicitly as:

28

$EI\frac{d^{4}u\left(x\right)}{d{x}^4}+P\frac{d^{2}u\left(x\right)}{d{x}^2}+k_{1}u\left(x\right)-k_2\frac{d^{2}u}{d{x}^2}=q\left(x\right),$

where $x$ is the axial coordinate axis, $u\left(x\right)$ is the deflection of the beam in the $z$ direction, $k_1$ and $k_2$ are the two-parameters of the two-parameter foundation, $I$ is the moment of inertia, $E$ is the Young’s modulus of elasticity of the beam material, $P$ is the compressive load, $q\left(x\right)$ is the distribution of transverse load on the beam.

Dividing by $EI$ gives:

29

$\frac{d^{4}u}{d{x}^4}+\frac{P}{EI}\frac{d^{2}u}{d{x}^2}-\frac{k_2}{EI}\frac{d^{2}u}{d{x}^2}+\frac{k_1}{EI}u\left(x\right)=\frac{q\left(x\right)}{EI},$

30

$u^{iv}\left(x\right)+\alpha u^{\text{'}\text{'}}+{\beta }_2{u}^{\text{'}\text{'}}\left(x\right)+{\beta }_{1}u\left(x\right)=\frac{q\left(x\right)}{EI},$

where:

31

$\alpha =\frac{P}{EI},{\lambda }_2=\frac{k_2}{EI},{\lambda }_1=\frac{k_1}{EI}.$

When no transverse loading acts, $q\left(x\right)=0,$ and Eq. (9) becomes a homogeneous ODE:

32

$u^{iv}\left(x\right)+(\alpha -{\lambda }_2)u\text{'}\text{'}\left(x\right)+{\lambda }_{1}u\left(x\right)=0.$

3. Methodology

The Fourier series method assumes that the unknown displacement $u\left(x\right)$ is in the form of a Fourier series given by:

where $A_n$ and $B_n$ are the coefficients of the Fourier series.

The thin beam considered is simply supported at the ends $x=$0, and $x=l.$

The boundary conditions are:

The force boundary conditions are:

Hence from the bending moment deflection equation of Euler-Bernoulli theory, the force boundary conditions are expressed in terms of the displacement variable as:

By differentiating $u\left(x\right)$ twice with respect to $x$, we have:

Applying the boundary condition Eq. (34a) gives:

Hence:

Applying the boundary condition Eq. (36a) gives:

Hence:

By differentiation of $u\left(x\right)$, we have:

Then, substituting into the governing equation yields:

Simplifying:

Orthogonalizing by multiplication by $\mathrm{s}\mathrm{i}\mathrm{n}\frac{m\pi x}{l}$ and integrating over the beam domain $(0\le x\le l)$ gives:

Simplifying, Eq. (45) gives Eq. (46);

Or:

where:

The sine functions are orthogonal. Hence, when $m\ne n$, $I_{mn}$ would vanish; but would not vanish when $m=n.$ The orthogonality conditions are:

if $m\ne n$ and non-zero if $m=n$:

The orthogonality conditions of the sinusoidal functions simplify Eq. (46) and enable the determination of the eigensolutions.

4. Results

The characteristic buckling equation is given from the conditions for nontrivial solutions to Eq. (47) by Eq. (49):

Solving for $\alpha$, by first simplifying Eq. (49) gives Eq. (50):

Further simplification of Eq. (50) gives Eq. (50a):

Dividing Eq. (50a) by ${\left(\frac{n\pi }{l}\right)}^2$ gives Eq. (51):

Simplifying Eq. (51) yields:

Hence:

Or:

Using Eq. (31) in Eq. (53a) gives:

Expressing Eq. (54) in the standard form gives Eq. (55):

Simplifying Eq. (55) gives Eq. (55a):

Hence introducing the dimensionless buckling coefficient $K({\lambda }_1,{\lambda }_2)$ gives:

where:

The critical buckling load coefficient $K_{cr}$ is the value of the least $K_{cr}$, and this occurs at the first buckling mode where $n=$1. Thus:

Then, the critical buckling load $P_{cr}$ which is associated with $K_{cr}$ is found as:

Values of $K_{cr}$ are calculated for certain nondimensional values of ${\stackrel{-}{k}}_1$ and ${\stackrel{-}{k}}_2$ expressed in terms of ${\lambda }_1$, ${\lambda }_2$ and $l$ and given in Table 1.

5. Discussion

This work has presented a first principles systematic derivation of the GDES for Bo2PFs. The GDES was derived using equilibrium Newtonian approach, and considered both translational and rotational equilibrium of an infinitesimal Bo2PF. The GDES is found as an ODE of fourth order.

This study has applied the Fourier series method to develop exact buckling solutions for simply supported Euler-Bernoulli beam resting on two-parameter elastic foundations of the Pasternak, Hetenyi, Vlasov or Filonenko-Borodich type. The GDES is a fourth order ODE which is non-homogeneous when transverse load is present, but homogeneous when transverse load vanishes, $q\left(x\right)=0.$

By assuming the unknown function $u\left(x\right)$ in the form of a Fourier series of unknown coefficients, and applying orthogonality of the Fourier series the GDES is reduced to a characteristic buckling equation given by the algebraic Eq. (49). The eigenvalue is found from the roots of Eq. (49) as Eq. (53) yielding the buckling load for any buckling mode, $n$, as Eq. (54).

Critical buckling load coefficient $K_{cr}$ is found to correspond to the first buckling mode $(n=1)$ and given by Eq. (58). Eq. (58) is presented in Table 1 for various values of the elastic foundation’s dimensionless two-parameters ${\stackrel{-}{k}}_1$ and ${\stackrel{-}{k}}_2,$ along with previous values of $K_{cr}$ determined by Taha [30], Anghel and Mares [35] and Ike [7], [9]. Table 1 illustrates that present FSM results are identical with the results obtained by Ike [7] by SVIM and using exact buckling shape functions and Ike [9] using fourth degree polynomial shape foundation in SVIM; Taha [30] results found by RDM, and Angel and Mares [35] results by Collocation method. The obtained solutions are exact within the framework of the Euler-Bernoulli beam stability equation considered because exact buckling shape functions were used and the solutions satisfied the domain equations at all solution points.

6. Conclusions

This study has presented first principles derivation using Newtonian equilibrium method for the elastic stability problem of Bo2PF.

This work has studied the FSM for solving the GDES for Bo2PFs. In conclusion:

1) The Fourier series method gives an exact analytical solution to the eigenvalue problem of simply supported beam on two-parameter foundations of the Pasternak, Hetenyi, Vlasov or Filenenko-Borodich type.

2) The critical buckling load occurs at the first buckling mode.

3) The critical buckling load expression is the exact analytical expression because the Fourier series contains the exact buckling shape function for the Dirichlet boundary conditions of the Bo2PF considered.

4) The results obtained for the critical buckling load parameters are identical with previous solutions that used SVIM, RDM and Collocation.