Seismic performance of fabricated shear wall structures with design defects

2.1. Establishment of analytical model

The analytical model employed in this study revolves around a 2-story prefabricated shear wall structure. Engineered to withstand a seismic fortification intensity of 7, the building’s site classification is designated as class II, accompanied by a seismic grade II rating. The geometric characteristics of the shear wall structure, depicted in Fig. 1, encompass planar dimensions of 3420 mm × 6000 mm, with each floor boasting a height of 3000 mm.

2.2. Establishment of calculation analytical model

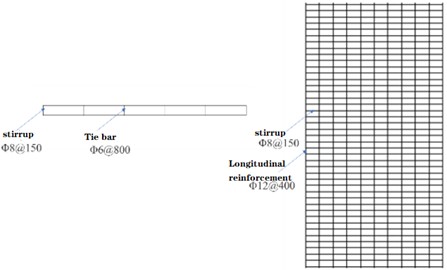
The analytical calculation model employed in this study revolves around on a 2-story prefabricated shear wall structure. Engineered the building to withstand a seismic fortification intensity of 7, the building’s site classification is designated as with a site classification of class II, accompanied by a seismic grade II rating. The geometric characteristics of the shear wall structure, depicted in Fig. 1, encompass planar dimensions of 3420 mm × 6000 mm, with each floor boasting a in planar size and have a floor height of 3000 mm. To connect with the lower structure, a reinforced concrete ground beam is positioned at the bottom. The concrete shear wall has a thickness of 210 mm, along with a protective layer thickness of 25 mm. The longitudinal reinforcement has a diameter of 12 mm and is spaced at intervals of 400 mm. Similarly, the stirrups have a diameter of 8 mm with a spacing of 150 mm. Additionally, tie bars with a diameter of 6 mm are installed between the longitudinal reinforcements, as illustrated in Fig. 2. The prestressed reinforcement has a diameter of 20 mm, while the grouting sleeve measures 400 mm in length and 60 mm in diameter.

Fig. 1Schematic representation of the shear wall structure

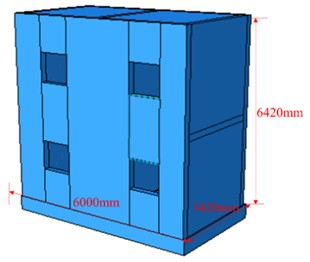
Fig. 2Reinforcing bar layout

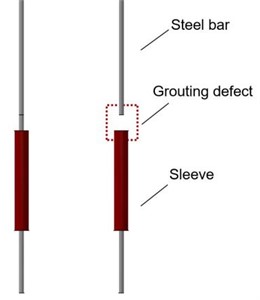
Considering that the grouting defect is a cylindrical cavity with a length of 64 mm, which is located at the upper end of the sleeve, where the concrete has no bonding effect with the prestressed reinforcement, as shown in Fig. 3.

The concrete utilized in the structure is C40 grade concrete, while the stirrups and tie bars are made of HRB300 reinforcement. The longitudinal reinforcements are made of HRB400 reinforcement. The fundamental properties of these materials are outlined in Table 1 for reference. A reinforced concrete ground beam resides at its base. The concrete shear wall exhibits a thickness of 210 mm, fortified by a protective layer measuring 25 mm in thickness. Longitudinal reinforcement components, fashioned with a 12 mm diameter, are spaced at 400 mm intervals. Complementary to this, stirrups, characterized by an 8 mm diameter, are situated at 150 mm intervals. Intertwining the longitudinal reinforcements are tie bars, elegantly portrayed in Fig. 2, bearing a diameter of 6 mm. Concurrently, the prestressed reinforcement element displays a diameter of 20 mm, while the grouting sleeve measures 400 mm in length and 60 mm in diameter.

Considering that the grouting defect manifests as a cylindrical cavity with a length of 64 mm, positioned at the upper extremity of the grouting sleeve. In this specific locale, the concrete's bond with the prestressed reinforcement is compromised, as depicted in Fig. 3.

Fig. 3Visualization of grouting defects within the structure

The structural components are assembled using C40 grade concrete, HRB300 reinforcement for stirrups and tie bars, and HRB400 reinforcement for longitudinal components. Pertinent material properties are concisely outlined in Table 1 for quick reference.

2.3. Establishment of finite element model

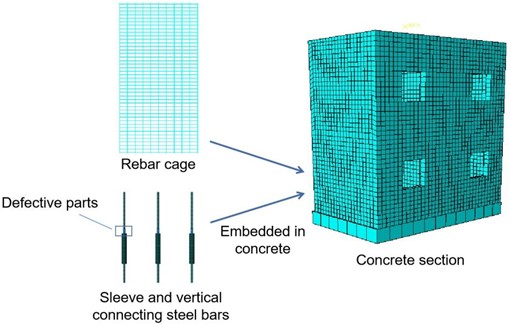
The construction of the finite element model was executed in accordance with the dimensional specifications outlined above. The Concrete Plastic Damage Model (CDP Model) was employed to replicate the behavior of concrete materials. Notably, the CDP model adeptly captures the evolution of concrete damage across cyclic loading conditions. The simulation of steel components was realized through a double line model. The discretization of the model was achieved using distinct element types: the C3D8R solid element was chosen for both concrete and prestressed reinforcement, the S4R shell element for sleeves, and the T3D2 truss element for reinforcement cages. For shear walls afflicted with grouting defects, meticulous attention was given to the precise definition of void regions within the mesh.

The assembly of the finite element model ingeniously incorporates the steel cage framework, sleeves, and interconnecting steel bars within the concrete wall matrix. In instances where sleeve grouting defects were simulated, material properties remained unspecified within the defective segment, deliberately disassociating it from the concrete matrix. In effect, this region assumed the role of a distinct defect. It is worth noting that the prestressed reinforcement within the flawed segment lacks any interaction with the adjacent concrete substrate. The schematic representation of this modeling process is visually expounded in Fig. 4.

Fig. 4Finite element model and modeling process

The overall structural configuration integrates the superstructure into a unified entity, anchored by the substructure's ground beam. The reinforcement elements and sleeves are integrated into the concrete. The model is categorized into two principal variants: those featuring comprehensive defects and those with partial defects. Specifically, the former exhibits seven defects on each side of the shear wall, while the latter displays three defects per side. These configurations are elucidated in Fig. 5.

Fig. 5Comparison of models with and without grouting defects

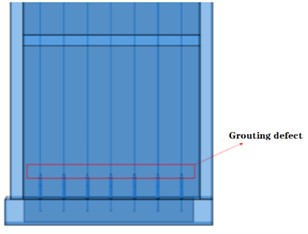
a) Model with comprehensive grouting defects

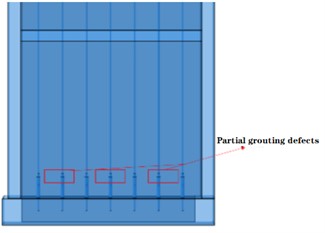
b) Model with partial grouting defects

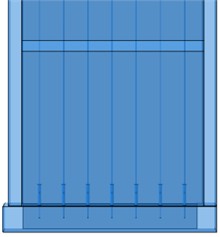
c) Model without grouting defects

3.1. Mode of structural loading

To investigate the impact of grouting defects on the overall structural stiffness and capacity for energy dissipation, analysis takes into account the angular displacement between elastic layers within distinct structures, as stipulated by the seismic design codes for buildings. The allowable displacement angle limit for concrete shear wall structures, as shown in Table 2, is set at 1/800. With the calculated model height of 6420 mm, this translates to a displacement limit of 8.025 mm for the uppermost section of the structure.

In the study, a displacement-controlled loading approach is employed. This allows for an exploration of the structure’s behavior beyond its elastic range. To enable this study, the peak loading amplitude is calibrated to 20 mm. Fixed constraints are imposed at the lowermost part of the structure. Furthermore, a coupling point is established at the model’s zenith to connect with the upper segment of the structure. At this coupling juncture, a reciprocating horizontal displacement (U1) is applied. The graphical representation of the loading protocol and the amplitude curve of displacement are elucidated in Fig. 6.

Fig. 6Schematic loading diagram and loading amplitude curve

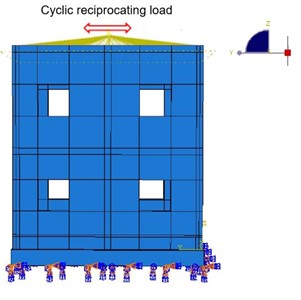
a) Loading diagram

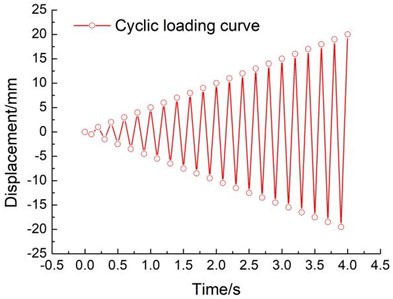
b) Loading amplitude curve

3.2. Analysis of concrete damage and reinforcement stress

Fig. 7 and Fig. 8 illustrate the nephogram s depicting the extent of concrete compression damage within the overall structure, both with and without grouting defects, respectively. In the plastic damage model employed for concrete, the damage factor signifies the extent of material damage in a particular region. Examination of these figures underscores a substantial elevation in concrete compression damage within structures afflicted by grouting defects, when compared to their defect-free counterparts.

Significantly, alongside the pronounced compression damage observed around the window area, there is also a noticeable increase in concrete compression damage adjacent to the defective section. From a frontal perspective, it is evident that the left and right segments of the window experience relatively diminished stress, resulting in the most profound concrete compression failure. Notably, in the structure with grouting defects, the shear wall opposite the window has progressed to a state of complete failure, whereas the concrete aligned with the window in the defect-free structure remains partially unaffected. Overall, concrete damage primarily manifests in the bottom structure, as observed in the nephograms.

Fig. 7Nephogram of concrete compressive damage nephogram (front view)

a) Defective structure

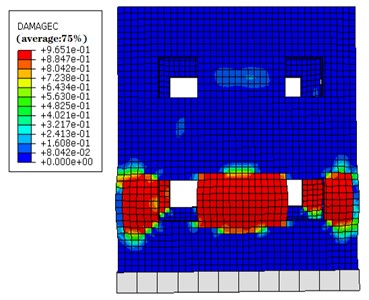
b) Defect-free structure

Fig. 8Nephogram of concrete compressive damage (side view)

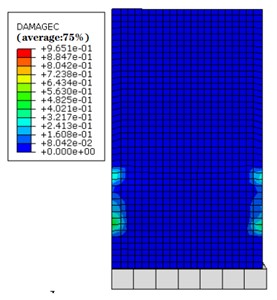
a) Defective structure

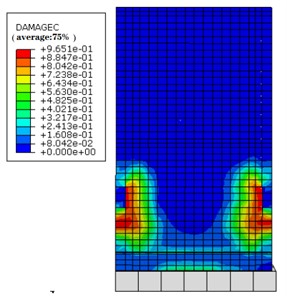
b) Defect-free structure

Upon applying cyclic loading for 10 cycles, the structure surpasses the maximum elastic displacement limit by 8 mm, transitioning from an elastic to an elastic-plastic state. Fig. 9(a) reveals that when the top displacement of the shear wall structure afflicted by grouting defects attains 10 mm, the concrete on both flanks incurs damage, exceeding its capacity, thus transferring the load incrementally to the reinforcement elements. The reinforcement stress nephogram in Fig. 9(a) indicates that as the concrete reaches its capacity, the longitudinal reinforcement concurrently attains a yield stress of 400 MPa. At this stage, the structural stress landscape is predominantly governed by the reinforcement stress. Conversely, the nephogram portraying concrete compression damage and reinforcement stress for the defect-free structure in Fig. 9(b) demonstrates that when the top displacement reaches 10 mm, the shear wall’s concrete sustains compression damage without outright failure, while the reinforcement stress below the yield threshold. Consequently, stress distribution within the structure is largely elastic, with only a marginal portion transitioning into the plastic domain.

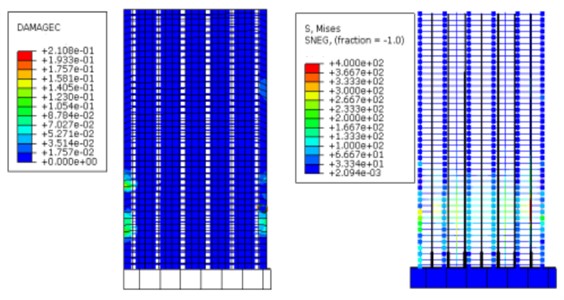
Subjected to 20 cyclic loads, the maximum displacement of the structure reaches 20 mm, surpassing the elastic displacement threshold significantly and pushing the structure into a plastic state. As shown in Fig. 10, the concrete damage of the structure with grouting defects surpasses that of the defect-free counterpart. The stress in the longitudinal reinforcement of the first layer of the structure attains 400 MPa, with an extensive plastic zone. In contrast, concrete damage in the defect-free structure is relatively minor, with the reinforcement reaching yield but a confined plastic zone, predominantly concentrated around the height of the front wall window. Due to the uniform defect distribution, specific damage tendencies emerge within certain defect models when defects are present or absent.

Fig. 9The nephogram of the shear wall under 10 times of cyclic loading

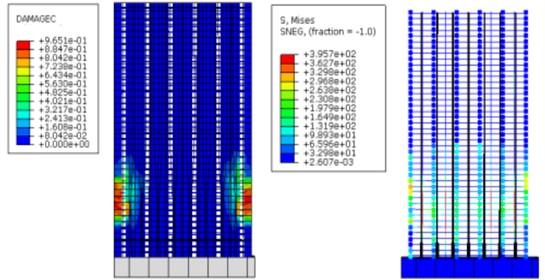
a) Nephogram of concrete compression damage and reinforcement stress of the structure with comprehensive defects

b) Nephogram of concrete compression damage and reinforcement stress of defect-free structure

By scrutinizing concrete damage and steel stress, a comparative evaluation emerges between the progression of damage and steel stress within shear wall structures, both with and without sleeve grouting defects, subjected to cyclic loading. It is evident that the presence of sleeve grouting defects induces slippage between steel bars and concrete within the defective sections, thereby amplifying damage across both compression and tension areas of the concrete. Premature detachment of concrete's load-bearing capacity imparts early stress onto steel bars, profoundly influencing the shear wall structure's macroscopic load-deformation capabilities.

3.3. Analysis of structural response-displacement relationship

This section delves into the assessment of shear bearing capacity performance in fabricated shear wall structures, focusing on changes in structural damage. The hysteresis curve represents the load-deformation relationship within structural components under cyclic loads. For a comparative evaluation of structures with and without defects, the load-displacement curves resulting from 10 and 20 times of cyclic loading are extracted, as depicted in Fig. 11. A meticulous examination of the load-displacement hysteresis curve of 10 times of cyclic loading, as depicted in Fig. 11(a), reveals a notably heightened “pinching phenomenon” in defective structures as opposed to their defect-free counterparts. This is attributed to the absence of adequate bonding between concrete and reinforcement due to grouting defects, triggering the slippage of prestressed reinforcement. Consequently, energy dissipation capacity diminishes, manifesting as the “pinching” behavior in the hysteresis curve. Moreover, when the structure reaches its yield point, the decaying reaction force in defective structures lags behind their defect-free counterparts. This divergence stems from early concrete damage in defect-affected zones, causing a loss of load-bearing capacity. The ensuing load is shouldered by prestressed reinforcement, reinforcement cage, and sleeve. The robust elastic modulus and yield stress of steel contribute to a relatively prolonged retention of reaction force, yielding a slightly slower decay in comparison to defect-free structures.

Fig. 10The nephogram of the shear wall under 20 times of cyclic loading

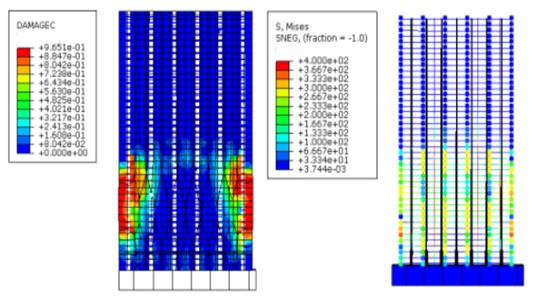
a) Nephogram of concrete compression damage and reinforcement stress of structure with comprehensive defects

b) Nephogram of concrete compression damage and reinforcement stress of defect-free structure

The hysteresis curves converge for both defective and defect-free structures as cyclic loading reaches 20 cycles, as indicated in Fig. 11. The prominence of the “pinching phenomenon” subsides in certain defect cases, with the presence of defect-free sleeves playing a pivotal role in this attenuation.

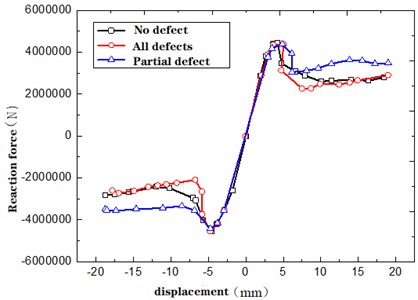
By connecting maximum reaction points across hysteresis curve stages, the load-displacement skeleton curve is delineated, as shown in Fig. 12. Evidently, the skeleton curves of structures, both with and without grouting defects, $c$ align extensively prior to reaching peak reaction force. However, the decay in reaction force is hastened in defective structures preceding the defect-free structures. Between displacements of 5-10 mm, defective structures exhibit a significantly accelerated decline in reaction force vis-à-vis the defect-free structure. Harmonization in skeleton curves occurs once structural displacement reaches 10 mm.

Fig. 11Hysteresis curves of structural reaction force-displacement

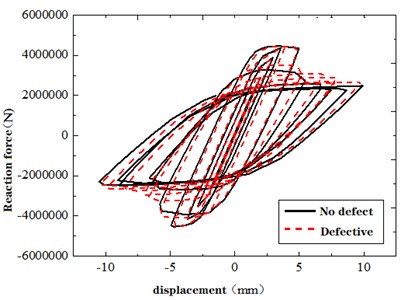
a) Ten-cycle loading of flawless and defective models

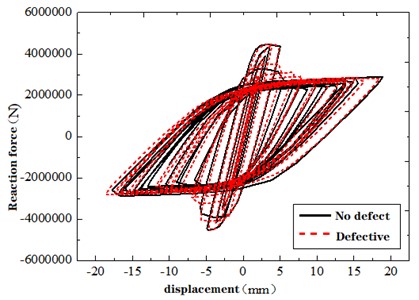
b) Twenty-cycle loading of flawless and defective models

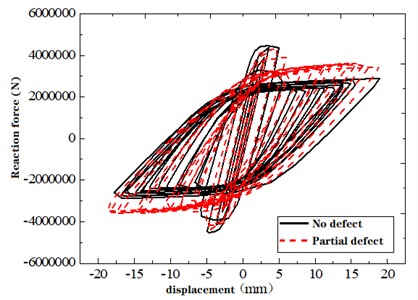
c) Twenty-cycle loading of models with no defects and partial defects

The seismic testing code of buildings specifies the use of the secant stiffness $K_i$ to represent the stiffness of the test specimen. Secant stiffness $K_i$ is calculated according to Eq. (1):

where, +$F_i$ and –$F_i$ denote loads pushed to and pulled to the peak point during the $i$-th cycle respectively; +${\mathrm{\Delta }}_i$, –${\mathrm{\Delta }}_i$ signify displacements pushed to and pulled to the peak point during the $i$-th cycle. Degradation is quantified by the ratio of secant stiffness to initial elastic stiffness.

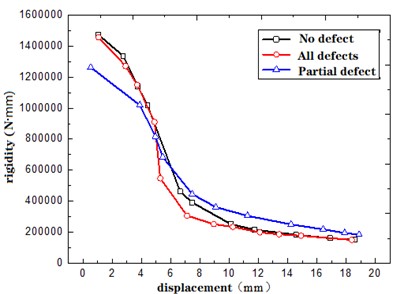
Stiffness degradation curves for defective structures and defect-free structures are illustrated in Fig. 13. It can be observed that in the elastic stage, the stiffness degradation rate of defective structure is basically same to defect-free structure. When the displacement reaches 5 mm, the structure starts transitioning from the elastic stage to the plastic stage. During the stage, the stiffness degradation rate of defect-free structure becomes faster than that of defective structures. This phenomenon can be attributed to the concrete in the defective areas of defective structures exits its load-bearing capacity earlier, and during the elastic-plastic transition stage, the load is primarily borne by the reinforcement. In contrast, the defect-free structure experiences stress redistribution between the reinforcement and the concrete during this stage, leading to accelerated degradation of structural stiffness.

Fig. 12Structural reaction force-displacement skeleton curve

Some defective structures manifest gradual stiffness degradation pre- and post- yielding. However, at displacements of 4-6 mm, stiffness degradation accelerates due to pre-yield interaction between reinforcement and concrete. As the yield displacement approaches, localized stress in defective zones prompts accelerated damage and structural stiffness degradation. Post-yielding, with concrete ceasing load-bearing, which are primarily borne by the reinforcement, the gradual shift in stiffness ensues.

Fig. 13Degradation curve of structural stiffness

By synthesizing microscopic plastic damage analysis with macroscopic mechanical performance analysis, insights into the altered seismic performance of shear wall structures with grouting defects can be explained.

Under cyclic loading, the concrete in the compression or tension areas of the structure with grouting defects will withdraw from the work in advance. This leads to an increase in the degree of fracture of the concrete around the defective area. Once the concrete is damaged, the reinforcement and sleeve take over the load-bearing role, resulting in premature yielding of the reinforcement. From a microscopic plastic damage perspective, the elastic section of the structure with grouting defects is shortened, while the plastic section is increased, expanding the range of the structural plastic deformation zone. The existence of defective areas causes slippage between the reinforcement and concrete, resulting in a more pronounced “pinching” behavior in the reaction displacement hysteretic curve.

Since defective structural reinforcement carries the external load prematurely, the skeleton curve pre- and post-yielding slightly surpasses that of defect-free structures. Upon full yield, however, both defective and defect-free structures align in hysteretic and skeleton curves. The swifter stiffness degradation in structures with grouting defects is attributed to premature concrete withdrawal and early transfer of load-bearing duty to reinforcements upon reaching yield.