Numerical simulation of heavy rail transit vehicle collision and analysis of collision force characteristics

2.1. Material model of heavy rail transit vehicle

In the process of collision, the main deformation of heavy rail transit vehicles is concentrated in the front part of the car, while the deformation of the middle and rear part of the car is small [10]. After referring to a large number of relevant literature, according to the performance and use of various material models, this paper finally selects the material model of heavy rail transit vehicle as *MAT_PLASTIC_KINEMATIC(MAT_3), another advantage of this model is that it can effectively simulate the failure of the vehicle due to the excessive stress of some components and the impact on the calculated structure during the collision [11]. Its strain rate effect is expressed by the following equation:

where ${\alpha \text{'}}_0$ is the deformation stress value of the heavy rail transit vehicle material; ${\alpha }_0$ is the static stress value; $b$ and $q$ are the strain rate parameters of the heavy rail transit vehicle material; $\dot{\beta }$ is the yield stress of the heavy rail transit vehicle material.

The parameters of the constitutive model of the head material of the heavy rail transit vehicle are shown in Table 1. The parameters in Table 1 are specifically described: $q_o$ is the density of the heavy rail vehicle material; $F$ is the Young’s modulus of the heavy rail vehicle material; $v$ is the Poisson’s ratio of the material; $F_t$ is the tangent modulus of the heavy rail vehicle material; $g_s$ is the heavy rail vehicle material.

The middle and rear parts of the vehicle body of heavy rail transit vehicles include carriages, girders and wheels, etc., and rigid connections are used between the various components [12]. The material constitutive model of the carriage, girder and wheel is set by the keyword *MAT_RIGID. Refer to the literature. The values of the material model parameters of the middle and rear parts of the car body are shown in Table 2, where, $M$ and $D$ are the plasticity values of the heavy rail vehicle material; $A$ is the mass constraint type parameter.

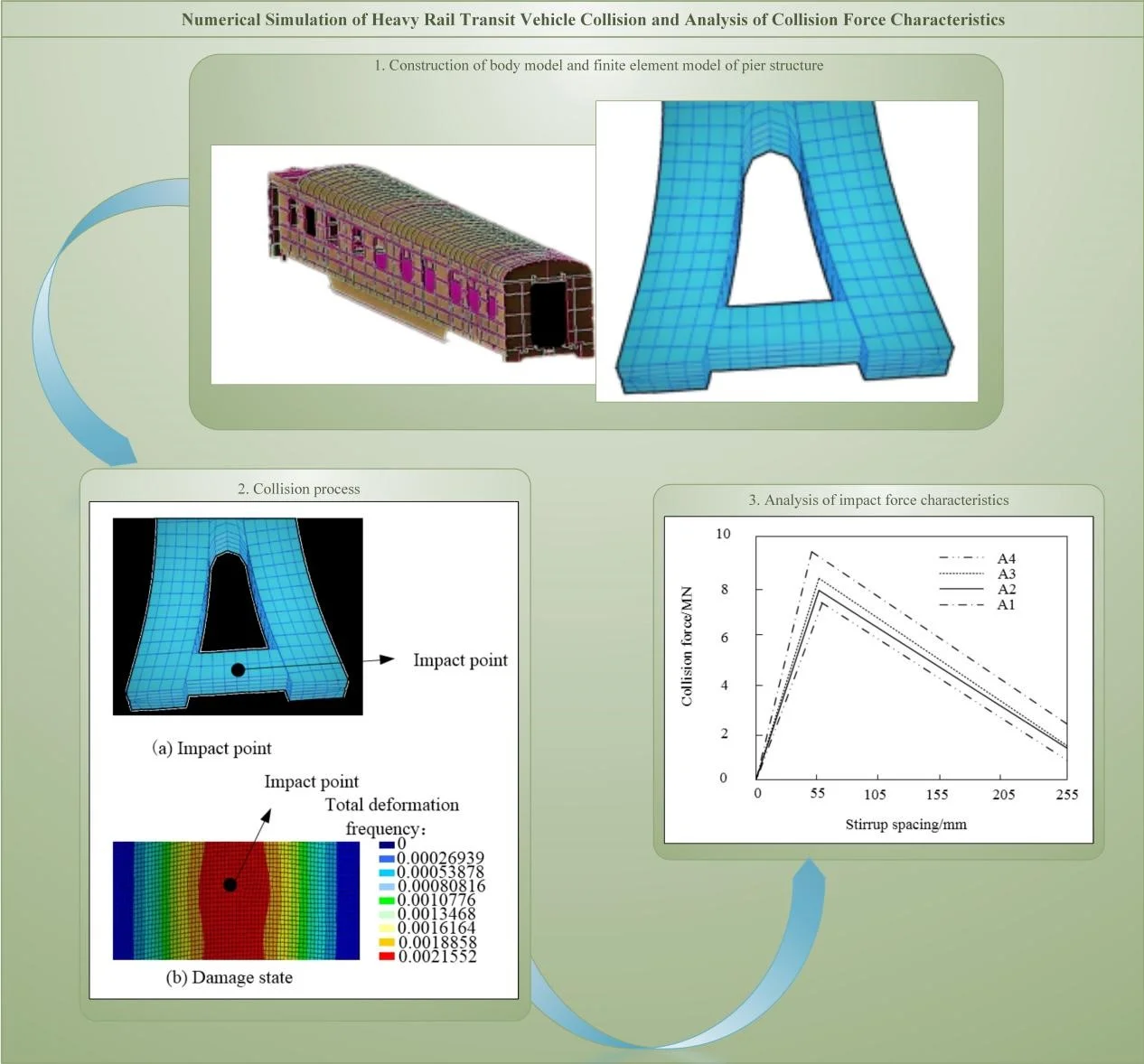
The body model is shown in Fig. 1.

Fig. 1Car body model

2.2. Bridge material mode

A typical urban bridge structure is selected as the research object. The upper structure is composed of bridge deck, guardrail, I-shaped main beam supporting the bridge deck, and spacer beam connecting the upper structure of two spans. The substructure of the bridge is composed of cover beams and double-column piers [13]. Since the bridge superstructure is not continuously poured, only the substructure and the two-span superstructure above it are simulated [14].

The bridge deck of the superstructure is 14.16 m wide and 0.3 m thick, supported by 6 I-shaped girders with a spacing of 2.5 m, the height of the guardrail is 0.84 m, and the height of the I-shaped girders is 1.15 m. The deck of the bridge adopts layered shell elements, distinguishing the steel layer and the concrete layer. Beam elements are used for concrete guardrails, I-shaped girders and partition beams, and discrete beam elements are used for rubber bearings [15]. Since the bridge colliding components studied are piers, and the failure mode of bridges subjected to vehicle collision has typical local effects, this paper does not consider the extreme cases of damage and fall of the superstructure [16]. The upper structure is made of linear elastic material, and the rubber support is made of nonlinear elastic material. This material allows the compressive stiffness to be defined in the vertical direction of the support, the tensile stiffness is zero, and the tensile and compressive stiffness is defined in the horizontal direction, and the element can be defined. When the substructure of the bridge fails, the superstructure and the substructure can be disconnected from the connection [17]. The finite element model of the bridge pier structure is shown in Fig. 2.

The steel material parameters of the substructure of the bridge are shown in Table 3.

Fig. 2Finite element model of bridge pier structure

2.3. Finite element software LS-DYNA

LS-DYNA is a world-renowned general-purpose display nonlinear dynamic analysis program capable of simulating various complex problems in the real world [18]. It has powerful analysis capabilities, rich material model library, easy-to-use cell library and adaptive meshing functions. It is especially suitable for solving geometric nonlinear, material nonlinear and contact nonlinear problems, such as explosion and impact, structural collision, metal forming problems [19]. It is mainly based on explicit analysis and supplemented by implicit analysis; it is mainly based on Lagrange algorithm, and has both ALE and Euler algorithms. It shows that the dynamic analysis adopts the central difference method, and the acceleration vector of each node of the structural system at the end of the $m$-th time step is calculated by the real formula:

Among them, $Q$ is the vehicle impact force on the pier structure at the end of the $m$-th time step (including the equivalent nodal force converted from the distributed load); $G^{\mathrm{i}\mathrm{n}\mathrm{t}}$ is the internal force vector of the bridge pier structure at the $t_m$-th time, which consists of the following items:

Among them, $A$ is the equivalent nodal force of the element stress field of the pier structure at time $t_m$; $G^{hg}$ is the hourglass resistance; $G^{contact}$ is the contact force vector when the pier collides with the vehicle.

2.4. Simulation test design

3.1. Finite element analysis results and analysis of the collision process

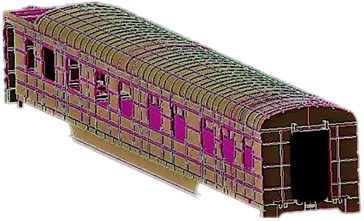
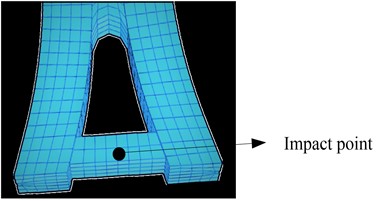
The 45 t vehicle is used to hit the bridge pier at a speed of 85 km/h. The impact point is shown in Fig. 3(a), and the damage status of the bridge pier during the collision is shown in Fig. 3(b).

Fig. 3Finite element analysis results of collision process

a) Impact point

b) Damage state

As shown in the figure, the total deformation frequency around the impact point of the bridge pier and the heavy rail transit vehicle decreases as the distance from the impact point increases, and the deformation frequency in the vicinity of the impact point is the largest.

Judging whether the above analysis results are correct is generally obtained by comparing experimental or engineering data, and the correctness of the finite element calculation itself can also be evaluated from the perspective of energy. Energy conservation is a criterion for judging whether the simulation results themselves are reasonable. Total energy = internal energy + kinetic energy + slip energy + hourglass energy, hourglass energy and slip energy should generally not exceed 10% of the internal energy. Here, only the energy change under a load of 10 t is selected for inspection. The time course of energy change is shown in Table 4.

During the impact process of the heavy rail transit vehicle hitting the bridge pier, the energy change is directly extracted from the calculation result by the software. When the time is 0.17 s, the total energy is 2.100×106 J, the kinetic energy is 0.045×106 J, and the internal energy is 1.978×106 J, so it can be seen that the sum of hourglass energy and slip energy is indeed lower than 10 % of the internal energy, which shows that the finite element analysis results are reliable.

3.2. Influence of vehicle speed on collision force

The change characteristics of the collision force with the speed change during the impact process of the heavy rail transit vehicle hitting the bridge pier are analyzed, and the simulation results are shown in Fig. 4.

Fig. 4Influence of vehicle speed on collision force

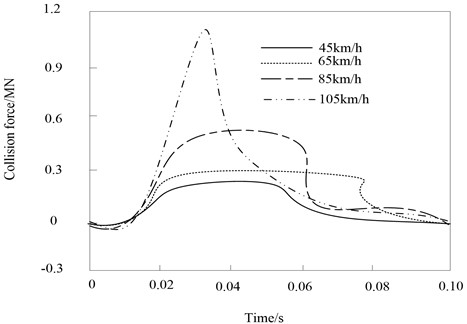
In the process of heavy rail transit vehicle impacting the pier, the peak value of vehicle impact force increases with the increase of vehicle speed. The peak value of impact force is the largest and the peak duration is the shortest at 105 km/h.

3.3. Influence of concrete strength of bridge piers on collision force

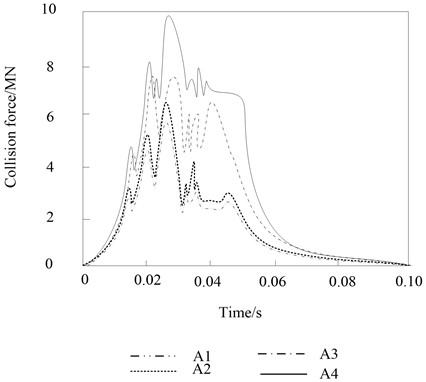
Fig. 5 shows the simulation results of the influence of the concrete strength of the bridge pier on the impact force during the impact process of the heavy rail transit vehicle hitting the bridge pier.

The peak size of the pier collision force of concrete A1, A2, A3 and A4 is A1 < A2 < A3 < A4. With the increase of concrete strength, the ductility of concrete decreases. During the impact process of heavy rail transit vehicles hitting the bridge pier, the structural deformation capacity of the bridge pier decreases, and the collision force increases.

Fig. 5Effect of concrete strength on impact force

3.4. Influence of stirrup spacing on collision force

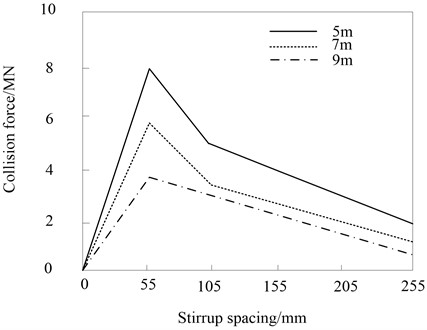
During the impact process of a heavy rail transit vehicle hitting a bridge pier, the peak value of the collision force under different bridge heights and stirrup spacings is shown in Fig. 6.

Fig. 6Peak value variation of impact force under different bridge height and stirrup spacing

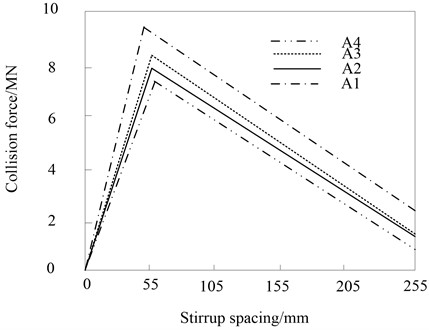
During the impact process of a heavy rail transit vehicle hitting a bridge pier, the peak value of the collision force under different concrete strengths and stirrup spacings is shown in Fig. 7.

With the densification of the spacing of the stirrups, the restraint capacity of the stirrups increases, and the strength of the concrete in the core area also increases, and the piers behave more rigidly under the impact of heavy rail transit vehicles, so the magnitude of the collision force increases. Especially when the stirrup spacing is about 55 mm, the restraint effect is more significant. For the piers of 5 m, 7 m and 9 m in Fig. 5, the peak value of the collision force with a stirrup spacing of 55 mm is larger than that with a stirrup spacing of 255 mm. The densification also reduces the amount of pier deformation during impact.

Fig. 7Peak value of impact force under different concrete strength and stirrup spacing

3.5. Influence of stirrup reinforcement ratio on collision force

In the impact process of the heavy rail transit vehicle hitting the bridge pier, the influence of the stirrup reinforcement ratio on the peak value of the collision force is shown in Table 5. Under the same impact, the structure with high stirrup reinforcement ratio appears “hard”, and the pier collides with higher force.

3.6. Influence of the eccentric distance between the vehicle and the bridge pier on the collision force

During the impact process of heavy rail transit vehicle impacting the pier, the simulation results of the impact of the eccentricity between the vehicle and the pier on the impact force are shown in Fig. 8.

The results show that during the impact process of the heavy rail transit vehicle hitting the bridge pier, when the cargo stiffness of the heavy rail transit vehicle is small, the peak value of the collision force under different collision eccentricities is relatively close. When the cargo stiffness is larger, there is a significant difference in the peak impact force in the second stage. This is mainly because when the eccentricity is large, the heavy rail transit vehicle directly collides with the bridge pier, and the peak value of the collision force is directly determined by the contact stiffness between the cargo and the bridge pier. Because the stiffness of the bridge pier is very large, high and narrow collision force will inevitably occur under the impact of the vehicle carrying the goods with greater stiffness. Therefore, when the rigidity of the cargo carried by the heavy rail transit vehicle is relatively large, the impact of the eccentric distance on the collision effect of the bridge pier should be carefully considered.

Fig. 8Influence of eccentricity between vehicle and pier on collision force

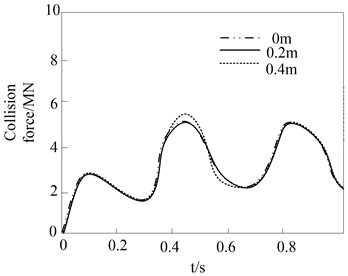
a) 15 MPa

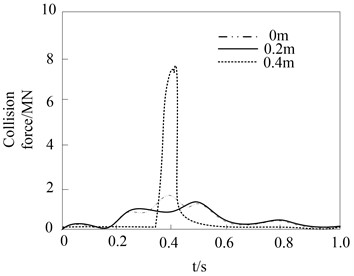
b) 10³MPa

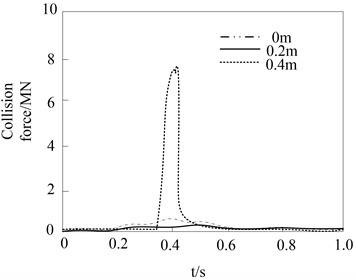
c) 10⁵MPa

3.7. Influence of vehicle mass on collision force

The simulation results of the impact of vehicle mass on the collision force are shown in Fig. 9.

Fig. 9Influence of vehicle mass on collision force

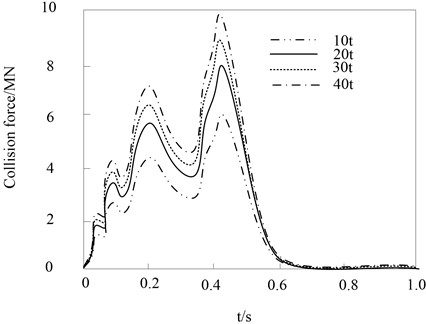
The results show that the time-history curves of the collision forces of different masses are roughly the same, and the four curves almost overlap at the initial stage of the collision. During the entire collision period, there will be large wave peak fluctuations around 0.45 s. The collision force then decreases drastically with time. This is because the front shell of the vehicle is in contact with the bridge pier at the initial stage of the collision. As the collision continues, the internal structure of the front of the vehicle will act, and the rigidity of the overall structure will increase to increase the collision force. The vehicle then rebounds and the impact force decreases with the impact time. And as the mass of the vehicle increases, so does the time at which the impact force time course ends. The reason is that the mass of the vehicle increases, the momentum at the same speed increases, and the impact force also increases.

4.1. The management of the team of drivers and passengers needs to be strengthened

Firstly, the professional quality of drivers and passengers needs to be improved. At present, most of the heavy rail car drivers in active service in China’s railway have no locomotive driving learning experience in colleges and technical secondary schools, lack of locomotive driving and corresponding maintenance theory, and there are more violations in the process of operation, which brings more risks to the use of heavy rail cars. Secondly, for the drivers and passengers, the operating standards in the process of work are unreasonable. Some drivers do not conduct the “five-step brake” test on the brakes before starting work, resulting in a serious shortage of pressure holding time [20]. When the main and auxiliary drivers monitor the data, there is no double-checking mechanism, so inconsistent data often appears on the display, which will cause the GYK monitoring device to open abnormally. During the work process, some drivers and passengers appear to have incorrect postures for answering calls and inconsistent voices. Thirdly, drivers and passengers are slow to respond to emergency problems. Drivers and passengers have relatively poor safety awareness in terms of safety risks and are not familiar with emergency procedures.

4.2. The quality of rail car equipment maintenance needs to be strengthened

First, the drivers and passengers of heavy-duty rail cars are not very aware of rail car maintenance. The daily maintenance of rail car couplers, drive shafts, brake cylinder pistons and other connecting parts is not in place, resulting in problems such as long-term non-drainage of the total air cylinder. The second is the lack of maintenance personnel. At present, there are only 2 people in the railcar maintenance team in the Baise Public Works Section, and one of them is a young worker who has been in the field for less than 3 years. The professional level is not high, and it is difficult to ensure the maintenance quality of heavy railcars. At the same time, due to the wide distribution of rail car parking points, after the equipment fails, the maintenance personnel cannot carry out the maintenance immediately, resulting in the heavy rail car waiting to be repaired for a long time, or even leaving the car with disease, which seriously affects the equipment quality and operation safety of the heavy rail car [21]. The third is that daily maintenance is a mere formality. Due to the heavy production tasks and difficult operation points of heavy-duty railcars, the heavy-duty railcars have to leave soon after they are parked and parked. Drivers and passengers often cope with maintenance and inspections on the grounds that there is not enough rest time to rush production tasks.

4.3. The professional management level of rail cars needs to be improved

Firstly, the effect of education and training is poor. After obtaining the theoretical certificate, most of the new recruits can only learn to operate the railcar by watching, and the practical experience is very lacking [22]. Workshop and related department managers did not participate in professional training, which is not conducive to professional management. The vocational education department did not establish a corresponding examination and analysis system, and did not carry out daily training work in combination with the actual situation on the spot, resulting in the lack of standardized guidance for the flight class by the section and workshop managers. Secondly, the professional management is not in place. The management department does not carefully judge the safety risks of rail cars, resulting in inadequate safety management and control, and poor on-site card control. The video analysis plan only conducts retrieval and analysis according to quantitative requirements. The coverage of retrieval and analysis is low, and it cannot play the due role of video surveillance. The rectification of the problems found in the inspection of the cadres was not reviewed in time, and the problems could not be managed in a closed-loop; the daily inspection of the management cadres was a mere formality, and the rules and regulations formulated were out of line with the actual production on site, which was not conducive to the operation of the flight shift, and directly affected the safety production of the flight shift. Thirdly, the production and transportation organization ability of heavy-duty rail cars is poor, the operation efficiency is low, and the operation points are difficult to coordinate. When the intermediate station is shunted, the station requires the co-driver to keep an eye on the duty room, to intervene at will to direct the production and transportation of railcars and other issues.