Abstract
A design of peel-speed sensitive flexible fastener was proposed based on a novel modified polyurethane. Taking the microtrichia of the head-arrester system of lestes barbarous as the bionic prototype, the structure of the micro protuberance was designed as self-mating type with hemispherical caps. Considering the nonlinearities of contact behavior and of the material property, a micromechanical model of typical interlocking element is established. Adopting the explicit dynamics finite element method, the mechanical responses of fastener in peeling are analyzed. The detachment of interlocking element is predicated by taking the total strain energy as an indicator. The influences of peel speed and friction coefficient on the mechanical performances are parametrically studied. The results show that the maximum peel force and the strength increased with respect to the enhancing peel speed because of the intrinsic nonlinearity in the constitutive relation of novel modified polyurethane the investigation adopted. With larger friction coefficient, the maximum peel force, the total strain energy and the corresponding de-adhesion displacements are respectively enhanced.
1. Introduction
The composite thin-walled deployable booms (CTDB) adopted to support the deployable membrane structures has been successfully realized its orbit application recently [1]. Flexible probabilistic fastener is the key component to control the deployment of the CTDB driven by the inflatable driving devices or by itself stored strain energy. Although the application of flexible fastener is extremely widespread, the available literatures on the mechanical research of flexible probabilistic fastener are quite few.
Applying the experimental and numerical method, Salama et al. [2] studied the mechanical behaviors of three types of fastener under the states of pure unlatching tensile stress and peeling loads. Wei et al. [3] studied the deployment responses of inflatable boom controlled by flexible fastener tapes that simulated by two-node rope element. Considering the influences of friction, Pugno [4] presented a nonlinear model to calculate the maximum attachment force, the nominal strength, and the toughness of flexible fasteners. Taking the driving velocity, applied normal load and hook numbers as control parameters, Mariani et al. [5] experimentally studied the frictional dynamics of the hook-and-loop system of Velcro® from the tribological point of view. Employing the micro-mechanical model, the deformation of the hooks and loops in the processes of engagement and detachment of flexible fasteners were analyzed in the research by Perezde [6]. To improve the adhesive properties and durability of mechanical interlocker, Jiao et al. [7] proposed an optimization design which has a pestle type micro protuberance. Sharma et al. [8] developed a soft probabilistic fastener which perceptibly reduced the damage of the protuberances or the mating fabric.
As can be seen, the research concentrated on the mechanical analyses of flexible fasteners is extremely insufficient compared to its widespread application. For the orbital deployable membrane structures, the characteristic of mechanical property of flexible fastener is quite crucial for controlling the in-orbit deployment of CTDB. According to the experimental result and daily usage experience, the loops of the most widely used hook and loop fastener would fracture or be pulled from the substrate after several attachment and detachment operations. It resulted in a reduction in the peel strength of fastener. Such instability of mechanical property is detrimental to the deployment stability of CTDB. Taking advantage of the elastic recovery behavior of CTDB, the self-deployment driven only by itself stowed strain energy can be realized by the appropriate design of mechanical characteristics of flexible fastener tapes. Considering the state of the art and the self-deployment control requirements of CTDB, a novel peel-speed sensitive flexible fastener is proposed and the mechanical properties are numerically analyzed.
2. Design and modeling
The neck of the adult dragonfly is very slender compared to the huge head. Although the strength of its head-neck joint is weak, its head can still flexibly rotate, pitch and yaw. The head can be firmly fixed and thus a stable field of view can be maintained even in tandem flight, aerial predation and grasping and biting prey. The biological investigations [9]-[11] show that plenty of microtrichia with different configurations (e.g., hook-shaped, cone-shaped and spindle-shaped) are distributed on the microtrichia field on back of head (mf) and the post-cervical sclerite (spc) of adult dragonflies. These microtrichia constitute the head-arrester system of adult dragonfly. During the high-intensity maneuvers, the microtrichia on the back surface of head will insert into the gaps between the microtrichia of the post-cervical sclerite. Attributed to the surface friction and mechanical restraint between these microtrichia, the temporary head fixation and an increased head stability can be ensured for the dragonflies which with the absence of antagonistic muscles.
As shown in Fig. 1, the microtrichia on the back of head and on the post-cervical sclerite are of the same configuration for lestes barbarus which belongs to the Lestidae family of Odonate Order. The head-arrester system of lestes barbarous has a high connection strength in the shear direction. Whereas the effect of motion constraint in the normal direction which provided by the surface friction forces is fairly weak. Taking the microtrichia of the head-arrester system of lestes barbarous as the bionic prototype, the fastener can be designed as self-mating type with ellipsoidal and spherical caps. Because of the similar mechanical mode, the connection strength in the normal direction of such fasteners are weak either.
Fig. 1Schemes of microhook in adult dragonfly head-arrester system [9]-[11]
![Schemes of microhook in adult dragonfly head-arrester system [9]-[11]](https://static-01.extrica.com/articles/22553/22553-img1.jpg)
a) Lestes barbarous
![Schemes of microhook in adult dragonfly head-arrester system [9]-[11]](https://static-01.extrica.com/articles/22553/22553-img2.jpg)
b) Head-neck scheme
![Schemes of microhook in adult dragonfly head-arrester system [9]-[11]](https://static-01.extrica.com/articles/22553/22553-img3.jpg)
c) Electron microscope image
![Schemes of microhook in adult dragonfly head-arrester system [9]-[11]](https://static-01.extrica.com/articles/22553/22553-img4.jpg)
d) Schematic representation
To enhance the ability of kinematic constraint and connection capabilities of interlocking elements, the structure of protuberances of flexible fastener are designed as self-mating type with hemispherical caps as shown in Fig. 2. Different from the hook-loop fastener, the pullout phenomenon of micro loop will not happen ever for such flexible fastener. Thus, it is of more stable mechanical properties and is more suitable for the deployment control of CTDB. In the subsequent sections, it will be taken as the object of mechanical property analysis.
The protuberance is quite small that its size is of the sub-millimeter level. Dozens of micro protuberances arranged on per square centimeter of fastener tape. Thus, the element sizes are very small when adopting the finite element (FE) method to characterize the mechanical properties of a flexible probabilistic fastener. Besides, the behavior of the contact between the interlocking elements is highly nonlinear. As a result, the cost of the computation will be extremely expensive if the full-scale sized FE model of fastener is adopted. The research by Cambridge University [12] shown that maximum peel force of a fastener with many micro protuberances can be approximated by the maximum peel force of a pair of interlocking elements multiplied by the number of protuberances. Therefore, a pair of interlocking elements will be taken as the representative mechanical cell to study the mechanical properties of a flexible fastener in the study.
A micromechanical model aiming to simulate the dynamic process of peeling was developed as shown in Fig. 3. All the freedoms of the outward surface of substrate of one fastener tape were constrained in peeling. The displacement load was applied to the outward surface of substrate of the mating fastener tape. The geometrical parameters of the flexible probabilistic mechanical fastener of the baseline group are detailed in Table 1. The experimental obtained constitutive relationship of novel modified polyurethane [13, 14] adopted in the research is plotted in Fig. 4.
Fig. 2Three-dimensional image of flexible fastener with hemispherical caps
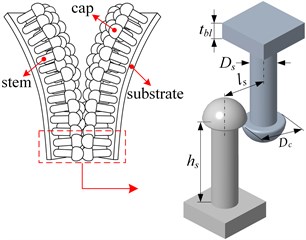
Fig. 3FE model of representative mechanical cell of the flexible fastener with hemispherical cap

Fig. 4Mechanical response of a novel modified polyurethane
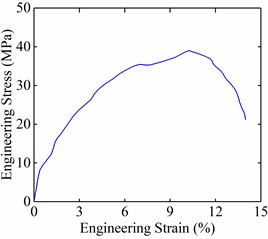
Table 1Structure parameters of mechanical interlocked fixing element with hemispherical cap
Parameter | Value |
Diameter of the stem of micro protuberance (mm) | 0.3 |
Hight of the stem of micro protuberance (mm) | 1.05 |
Distance between the stems of adjacent micro protuberances (mm) | 0.64 |
Diameter of the hemispherical cap (mm) | 0.5 |
Thickness of the substrate (mm) | 0.2 |
3. Numerical simulations and result discussion
With the adoption of explicit dynamical method, the process of peeling was analyzed. The circular planes of hemispherical caps of two mating micro protuberances get into contact first in peeling. Since the second moment of area of the hemispherical cap along the peeling direction was larger than that of the stem, most of the external input energy was converted into the bending strain energy of the stem. Thus, the deformation at the contact position was very small, and the circular plane of the hemispherical cap was basically perpendicular to the axis of the stem. As observed in the load-displacement curves plotted in Fig. 5(a), the peel force reached a peak value of 4.36 mN when the displacement increased to 0.0176 mm. Multiple extremum peaks occurred in the subsequent process of increasing peeling displacement. With further increase of displacement to 0.0647 mm, the maximum lateral deformation of the hemispherical cap of the upper protuberance occurred.
Integrating the load–displacement curve of the peeling process, the de-adhesion energy can be obtained mathematically. It can be seen from Fig. 5(b) that the de-adhesion energy rose to a peak value with increase in peeling displacement to 0.0658 mm. Adopting the locally weighted regression algorithm, the load-displacement curve was smoothed Fig. 5(a)). It can be observed that the peel force gradually decreased to 0 N as the loading displacement increased to 0.0658 mm. The values of peeling displacement were quite close when the maximum values of de-adhesion energy and maximum lateral deformation of the hemispherical cap reached. Nevertheless, considering the varying characteristics of the force-displacement curve, it is more reasonable to take the maximum de-adhesion energy as an indicator for predicting the detachment of flexible fastener.
Fig. 5Peel force and strain energy versus displacement for peel speed Vp= 30 mm/s
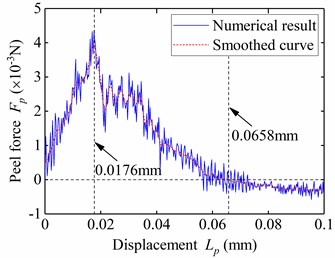
a) Peel force versus displacement for 30 mm/s
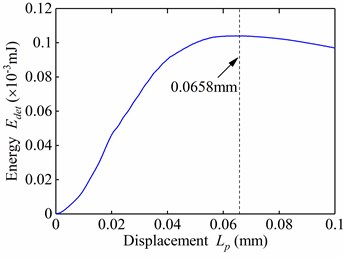
b) Strain energy versus displacement for 30 mm/s
3.1. Influences of the peel speed
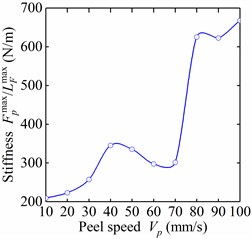
In the deployment of the CTDB which coiled on hub, the value of forward moving speed of hub along the boom axis does not remain constant. Thus, the peel speed of the flexible fasteners used to control the deployment of coiled boom also varies accordingly. 10 groups of detachment analyses at different peel speed are conducted in this section. As observed in Fig. 6(a), the mechanical behaviors were greatly influenced by the peel speed. The maximum peel force increased 81.9 % from 4.14 mN to 7.53 mN when the peel speed enhanced from 10 mm/s to 100 mm/s. The de-adhesion displacement when reached varied a lot in the process of speed growing. Furthermore, the slope of the force-displacement curve before the maximum peel force reached, i.e. the stiffness, were increased from 210 N/m to 668 N/m (Fig. 7). However, the total strain energy represented by the area under the load–displacement curve remains steady at about 1.05×10-4 mJ even the peel speed has increased 9 times (Fig. 6(b)). Meanwhile, the values of de-adhesion displacement when the maximum de-adhesion energy reached keep almost constant at 0.066 mm with small fluctuation.
It can be concluded that the mechanical property of the flexible fastener made by a novel modified polyurethane is very sensitive to the peel speed. Such speed sensitivity is mainly attributed to the strong nonlinearity of mechanical characteristics of the novel modified polyurethane the research adopted. With the aid of sensitive positive-correlation between the peel speed and peel force of fastener, the self-deployment of CTBM, driven only by the strain energy stored in boom and controlled by flexible fasteners, can be remained at a certain steady speed.
Fig. 6The influences of peeling velocity on mechanical properties of fastener
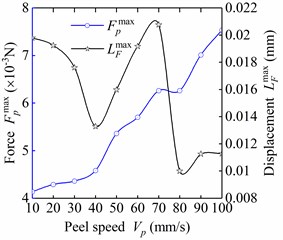
a) Maximum peel force and corresponding displacement
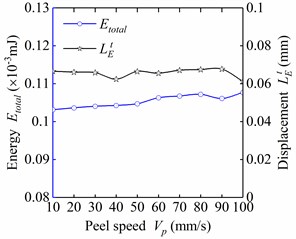
b) Maximum peel force and corresponding displacement
Fig. 7The influences of peel speed on stiffness
3.2. Influences of the friction coefficient
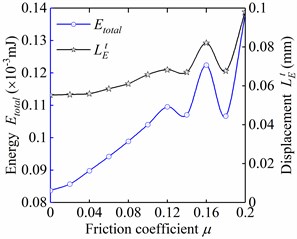
In this section, 11 groups of dynamic analyses of detachment at different friction coefficient of mating caps are conducted. As the friction coefficient slightly increased to 0.02, the maximum peel force and total strain energy were relatively small with the value of 4.09 mN and 8.57×10-5 mJ, respectively (Fig. 8).
Fig. 8The influences of friction coefficient on mechanical properties of fastener
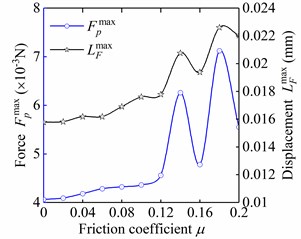
a) Maximum peel force and corresponding displacement
b) Maximum peel force and corresponding displacement
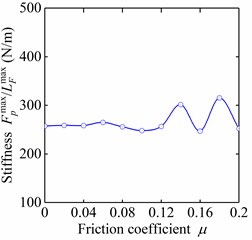
With the increase in friction coefficient, the frictional force between the hemispherical surfaces of two interlocking protuberance caps gradually increased. As a result, the external load required to release the fastener was increased. At the same time, the deformation of the stems in the peeling direction increased, and consequently also the strain energy and the friction dissipation. From the load-friction coefficient curve illustrated in Fig. 8, it can be observed that the maximum peel force and total strain energy increased with the increase of the friction coefficient in general. For a larger friction coefficient with the value of 0.2, the maximum peel force and the total strain energy were, respectively, increased to 5.55mN and 1.38×10-4 mJ with 36.7 % and 64.8 % increase when compared with those for the small friction coefficient 0. In addition, the displacements and corresponding to and also increased by 39.6 % and 77.4 %, respectively. However, the slope of the force-displacement curve before the maximum peel force reached, i.e. the stiffness, were almost remain steady at 265 N/m (Fig. 9). Overall, the mechanical properties of the flexible fastener were significantly varied under the impact of the change of surface roughness of micro-protuberances.
Fig. 9The influences of friction coefficient on stiffness
4. Conclusions
The maximum peel force and stiffness of the flexible fastener made by a novel modified polyurethane are sensitive to the peel speed. While the total strain energy and the corresponding de-adhesion displacement remain steady with the increasing peel speed. The mechanical properties of the flexible fastener are significantly influenced by the change of surface roughness of micro-protuberances. The maximum peel force, the total strain energy and the corresponding de-adhesion displacements increase with friction coefficient. The stiffness remains steady in the enhancing process of friction coefficient.
References
-
M. K. Chamberlain, S. H. Kiefer, M. Lapointe, and P. Lacorte, “On-orbit flight testing of the Roll-Out solar array,” Acta Astronautica, Vol. 179, pp. 407–414, Feb. 2021, https://doi.org/10.1016/j.actaastro.2020.10.024
-
M. Salama, H. Fang, and M. Lou, “Resistive deployment of inflatable structures using Velcro,” Journal of Spacecraft and Rockets, Vol. 39, No. 5, pp. 711–716, Sep. 2002, https://doi.org/10.2514/2.3869
-
J.-Z. Wei, H.-F. Tan, H.-W. Sun, and X.-W. Du, “Simulation and experiment for inflatable control deployment of rolled booms,” in 51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 18th AIAA/ASME/AHS Adaptive Structures Conference 12th, pp. 1–11, Apr. 2010, https://doi.org/10.2514/6.2010-2580
-
N. M. Pugno, “Velcro® nonlinear mechanics,” Applied Physics Letters, Vol. 90, No. 12, p. 121918, Mar. 2007, https://doi.org/10.1063/1.2715478
-
Mariani M. L., Esposito M. C., and Angiolillo J. P., “Observations of stick-slip friction in Velcro®,” Tribology Letters, Vol. 56, No. 2, pp. 189–196, 2014.
-
Perez V. R., “Multiscale strategy for modelling the mechanical performance of hook and loop fasteners based on a detachment process zone model,” Purdue University, Indiana, 2016.
-
J. Jiao, F. Zhang, T. Jiao, Z. Gu, and S. Wang, “Bioinspired superdurable pestle-loop mechanical interlocker with tunable peeling force, strong shear adhesion, and low noise,” Advanced Science, Vol. 5, No. 4, p. 1700787, Apr. 2018, https://doi.org/10.1002/advs.201700787
-
P. Sharma, V. Saggiomo, V. van der Doef, M. Kamperman, and J. A. Dijksman, “Hooked on mushrooms: Preparation and mechanics of a bioinspired soft probabilistic fastener,” Biointerphases, Vol. 16, No. 1, p. 011002, Jan. 2021, https://doi.org/10.1116/6.0000634
-
Gorb S. N., “Ultrastructural architecture of the microtrichia of the insect cuticle,” Journal of Morphology, Vol. 234, No. 1, pp. 1–10, 1997.
-
S. N. Gorb, “Evolution of the dragonfly head-arresting system,” Proceedings of the Royal Society of London. Series B: Biological Sciences, Vol. 266, No. 1418, pp. 525–535, Mar. 1999, https://doi.org/10.1098/rspb.1999.0668
-
S. N. Gorb, “Biological and Biologically Inspired Attachment Systems,” in Springer Handbook of Nanotechnology, Berlin, Heidelberg: Springer Berlin Heidelberg, 2010, pp. 1525–1551, https://doi.org/10.1007/978-3-642-02525-9_43
-
J. A. Williams, S. G. Davies, and S. Frazer, “The peeling of flexible probabilistic fasteners,” Tribology Letters, Vol. 26, No. 3, pp. 213–222, Apr. 2007, https://doi.org/10.1007/s11249-006-9187-4
-
J. Fan and A. Chen, “Studying a flexible polyurethane elastomer with improved impact-resistant performance,” Polymers, Vol. 11, No. 3, p. 467, Mar. 2019, https://doi.org/10.3390/polym11030467
-
S. F. Ali and J. Fan, “Capturing dynamic behaviors of a rate sensitive, elastomer with strain energy absorptions and dissipation effects,” International Journal of Applied Mechanics, Vol. 13, No. 9, pp. 1–10, Nov. 2021, https://doi.org/10.1142/s1758825121501040
About this article
This research is supported by the Shanghai Post-doc Excellence Program (2020199), Civil Aerospace Technology Research Project of National Defense Technology Industry Bureau (D020205, D010103).
