Abstract
The mode characteristics and the parameter sensitivity for a two-stage NGW spur planetary gear system are studied based on the principles of structure natural dynamical characteristics. Considering the influence of flexible structure including shaft, the planet carrier, and the ring-gear, the coupled lateral-torsional-axial vibration dynamical model of the planetary gear system is established under the generalized coordinate system using the shafting element method. With the model, the natural frequency and vibration mode are solved, and the results indicate that the flexibility of ring-gear has a greater effect on natural frequency. Several distinct types of vibration mode are summarized, such as planet torsional mode, sun-gear shaft axial mode, ring-gear axial mode and so on. However, the translational mode which is one of the modes in the coupled lateral-torsional lumped mass model is not found in this study. Within the scope of the time-varying, mesh stiffness mainly affects the planet torsional mode of corresponding stage. Furthermore, the variation of radial bearing stiffness will also do effect on axial vibration mode, and the variation of bearing stiffness not only affects the vibration modes of adjacent stage of planetary gear train, but also affects the nonadjacent stage. The results demonstrate the coupling characteristics of the system under the free vibration condition.
1. Introduction
Planetary gear transmission has many advantages, such as its compactness, light weight, heavy carrying capacity, large transmission ratio, and high-transmission efficiency. Hence, it is extensively used in both high-speed, large power, and low-speed, high-torque applications, such as automobiles, helicopters, marine main reducers, engineering machinery, lifting transportation, and other related machineries. The vibration and noise problems of multi-stage planetary gears are always the focus of attention by both academics and engineers [1]. And the prediction of natural modes, as one of the major issues in vibration field, has increasingly attracted extensive attention because of the desire to design a highly reliable, low-vibration planetary gear system.
The early literature about the natural characteristics analysis of planetary gear is scarce. Cunliffe [2] studied the eigenvalue problem for a thirteen degree of freedom system and identified the natural frequencies and vibration modes in 1974, and Botman [3] investigated the vibration modes for a spur planetary gear with eighteen degrees of freedom in 1976, but they didn’t give general conclusions. Then, Lin and Parker [4, 5] formally identified and proved the vibration structure of planetary gears with equal/ unequal planet spacing. They analytically classified all planetary gears modes into exactly three categories, rotational modes, translational modes, and planet modes. Wang Shiyu [6] investigated the inherent property of planetary gear trains with equal planet spacing, and discovered the phenomenon of vague vibration mode when some parameters taking the particular values. Furthermore, the above rule of modes classification would no longer be applicative for the system with concentrated eigenvalue. Zhang Jun [7] revealed the deductive errors in Lin’s model, and proposed the modified dynamic model which can reveal the free vibration characteristics of the planetary gear system more accurately. Kahraman [8] established a family of torsional dynamics models for compound planetary gears under different kinematic configurations. Kiracofe and Parker [9] developed a dynamic model of compound planetary gears of general description including translational degrees of freedom, which allows an infinite number of kinematic combinations. And it was mathematically proved that the modal characteristics of compound planetary gears were analogous to a simple, single-stage planetary gear system.
According to the aforementioned models and vibration structure of planetary gears, many researchers concerned the sensitivity of the natural frequencies and vibration modes to system parameters. They investigated the effect of modal parameters such as mesh stiffness and planet bearing stiffness on natural frequencies and vibration modes of planetary gear. Parker [10, 11] mathematically analyzed the effects of design parameters on natural frequencies and vibration modes and the following conclusions were drawn: (1) Rotational modes are independent of the transverse support stiffnesses. (2) Translational modes are similarly independent of the rotational support stiffnesses. (3) Planet modes are insensitive to all carrier, ring, and sun support stiffnesses.
However, there are mainly three aspects of problem in the existing research literatures as following: (1) Most of the models were established using the lumped mass method, and the main shortcoming of the modeling approach is low-fidelity. (2) In the model of spur planetary gear system, only radial and torsional degrees of freedom were considered, and the axial freedom was ignored. This may lead to the loss of some coupling characteristics of the overall system. (3) Most of the current studies only referenced the method used for single-stage planetary gears to analyze the modal characteristics of multi-stage planetary gears, while the differences between these two types of planetary gears were ignored. In this paper, the coupled lateral-torsional-axial vibration dynamical model of a two-stage NGW spur planetary gear system is established under the generalized coordinate system using the shafting element method. The coupling relationship amongst different freedoms, system nodes, major structural components, and stages in the analysis of the planetary gear natural characteristics is fully considered in order to accurately and reliably understand the dynamic behavior in the multistage planetary gear system. Sensitivity of the natural frequencies and vibration modes to system parameters is studied, and it will provide important information for tuning resonances away from operating speeds, minimizing response, and optimizing the structural design.
2. Shafting element method
2.1. Division of multistage planetary gear system
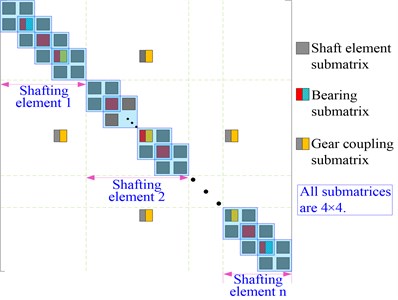
The multistage planetary gear system is composed of multiple connected components, and it is a nonlinear system with complex coupling factors. Only all the parts are taken into account, the real dynamic characteristics will be obtained [12]. Fig. 1 illustrates a typical multistage planetary gear transmission system consisting of the shaft, bearing, sun gear, planet gear, ring gear, planet carrier, and other related structural components.
Fig. 1Division of multistage planetary gear system
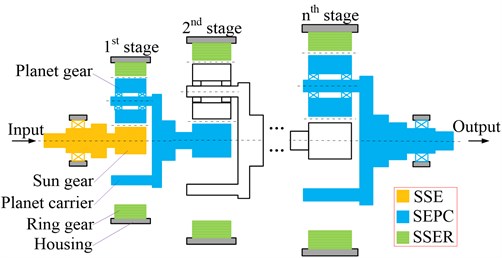
In order to formulate the equation of dynamic motion of the entire structure, the system can be divided into shafting elements, based on three categories, according to its structural characteristics: (1) Simple shafting element (SSE), to represent the actual shaft with the virtual equivalent shaft. (2) Shafting element of planet carrier (SEPC), to model the flexibility of the carrier. (3) Special shafting element of ring (SSER), to represent the flexibility of the ring gear.
2.2. Simple shafting element
Every simple shafting can be divided into many elastic shaft segments. And the gear shaft can be equivalent to virtual shaft element based on the modeling similarity principle and dynamic similarity theory [13, 14], as shown in Fig. 2. Assuming that both of the two nodes of the shaft segment would bear a bending moment, torque, and an axial force, then the stress condition of the shaft segment can be analyzed by employing the Euler-Bernouli beam element theory [15], as shown in Fig. 3. Four degrees of freedom are considered in the coupled lateral-torsional-axial vibration dynamical model of the planetary gear system.
Fig. 2Equivalent virtual shaft segment of gear shaft
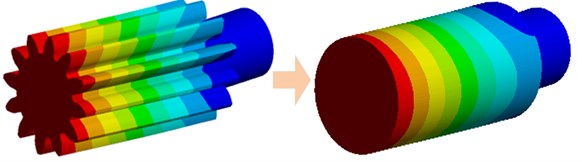
Fig. 3Simple shafting element model
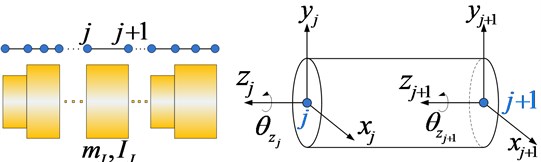
Given that is the displacement vector of the two nodes of Euler-Bernouli beam element in the local coordinate system, the free vibration equation of the element can be expressed in accordance to Eq. (1):
In Eq. (1), denotes the mass matrix, in which and , and , respectively denote the mass and moment of inertia of the Euler-Bernouli beam element . The Euler-Bernouli beam element stiffness matrix has a 8×8 order form and can be formulated by using the related theory of elastic mechanics, as expressed by Eq. (2).
In Eq. (2), denotes the cross-sectional area of the beam element, denotes the elastic modulus of materials, denotes the element length, denotes the shear modulus, denotes the torsional moment of inertia, and denotes the cross-sectional moment of inertia, denotes the shear impact factor, and . For the shear coefficient , it is assumed that for the circular section, , and for the rectangular section, [16]. In Eq. (1), the material damping is assumed as classical damping, which can be derived from Eq. (4) as:
where , denote the scale factors.
2.3. Flexible model of planet carrier
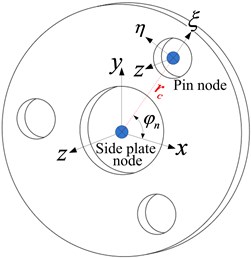
In the planetary gear system, the flexibility of the planet carrier may have an important influence on the gear meshing quality and reliability of both the internal and external gear pairs [17, 18]. Single-side plate-type and double-side plate-type are two common forms of the planet carrier. A single-side plate-type of a planet carrier can be seen as the substructure of the planet carrier with a double-side plate. Therefore, only the double-side plate-type carrier is analyzed, as shown in Fig. 4.
Fig. 4Shafting element of the planet carrier
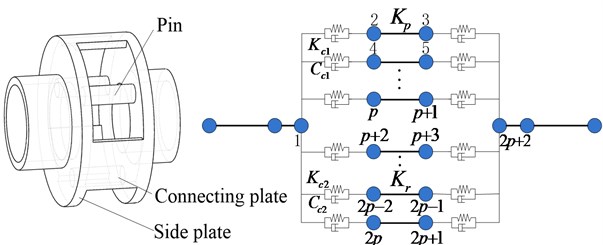
In simple terms, the shafting element of the planet carrier has an additional coupling matrix between the two side plates than the simple shafting element. The mass matrix, stiffness matrix, and damping matrix between the two side plates are defined as , , , respectively. Assume that there are pins and connecting plates, and there are nodes between the two side plates labeled as 1 to . The pin is equivalent to the circular cross-section beam element whose stiffness matrix can be denoted as . The nodes on both sides of the pin are respectively coupled with nodes 1 and of the two side plates, and the corresponding coupling stiffness matrix is . In the same way, the connection plate is approximately equivalent to the rectangular cross-section beam element whose stiffness matrix is represented by , and the coupling stiffness matrix with side plates is :
represents the overall mass matrix. The forms of and are both consistent with , which can be expressed as Eq. (4).
The pin-side plate coupling is shown in Fig. 5 where is the center distance between the pin and the side plate, and denotes the position angle of the pin (or planet gear). The coupling stiffness matrix between the pin and the side plate can be deduced in accordance to Eq. (5):
where denotes the coupling stiffness values with four degrees of freedom. The derivation methods for is identical which can be expressed as:
Fig. 5Schematic diagrams of the pin-side plate coupling
The overall stiffness matrix can then be expressed in accordance to Eq. (7), and the form of is consistent with :
The planet gear and pin are coupled through the bearing element, and the coupling stiffness matrix can be expressed as:
where denotes the stiffness matrix of the bearing element only with the main item retained. Similarly, the form of the damping matrix is consistent with .
2.4. Flexible model of ring gear
Many prior studies have shown that the flexibility of the ring gear can be a major influence on the dynamic performance of the planetary gear system [19, 20]. And the transmission reliability and service life might be influenced. Therefore, given these discrepancies, it is desirable that the dynamic performance of the system can be more accurately determined when considering the flexibility of the ring gear.
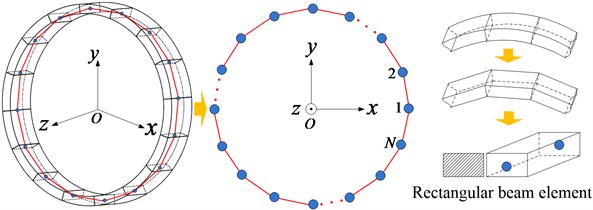
The ring gear can be equivalent to virtual shaft element first similarly with gear shaft, as shown in Fig. 6. And then the special shafting element of the ring can be divided into discrete shaft segments as shown in Fig. 7. , where denotes the tooth number of the ring gear, and is defined as the flexibility coefficient. Usually, is also equal to an integer number of times of the planet gear number to ensure the symmetry of the system’s structure. Furthermore, every shaft segment can be approximated as a rectangular beam element, and the coupling stiffness of adjacent nodes can be calculated by employing the Euler-Bernoulli rectangular beam element theory.
Fig. 6Equivalent virtual shaft segment of ring gear
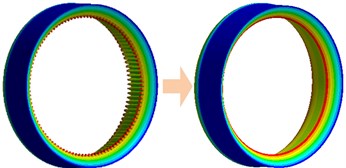
Fig. 7Special shafting element of ring gear
2.5. Overall system model
As shown in Fig. 8, three types of coordinate systems are included in the generalized coordinate system: (1) the static coordinate system , (2) the moving coordinate system rotating with the carrier, and (3) the moving coordinate system rotating with the carrier, where is in the radial direction and is in the tangential direction [21].
The SSE with the sun gear node included, and the SEPC with the planet gear node included, are coupled by external gearing. Similarly, the SEPC with the planet gear node included, and the SSER with the ring gear node included, are coupled by internal gearing. The projection vector along the mesh line along the action direction transformed at various degrees of freedom of the meshing pair can be expressed in accordance to Eq. (9):
where , , denote the base circle radii of the sun gear, planet gear, and ring gear respectively, is the angle between the normal direction of the meshing line and the positive -axis which can be expressed as . The plus or minus sign changes as the sun gear direction of rotation alters [22]. And denotes the meshing angle, denotes the installation phase angle of the planet gear. Subsequently, the stiffness matrix of the meshing coupling element can be expressed as , where is the normal synthetic meshing stiffness.
Under the overall generalized coordinate system, vibration equations of shafting elements in the multistage spur planetary gear system can be directly lumped, according to the rules shown in Fig. 9, to form the free vibration equation of the system as:
where , , are the total mass, damping, and stiffness matrices, respectively.
Fig. 8The generalized coordinate system
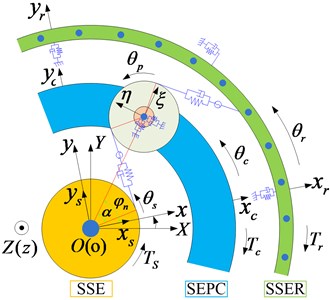
Fig. 9Schematic diagram of the assembly rules
3. Mode characteristics analysis
3.1. Model of a two-stage spur planetary gear system
For the computational study, a two-stage spur planetary gear system is considered with the essential parameters given in Table 1. The mesh stiffness and bearing stiffness are shown in Table 2 and 3, respectively. And the 3D model is shown in Fig. 10.
Table 1Two-stage planetary gear system data
Sun gear | Planet | Ring gear | ||
Number of teeth | 1st stage | 12 | 47×3 | 108 |
2nd stage | 54 | 26×3 | 108 | |
Module (mm) | 1st stage | 1.25 | ||
2nd stage | ||||
Pressure angle (deg) | 1st stage | 25.0 | ||
2nd stage | ||||
Table 2Mesh stiffness
External meshing (N·m-1) | Internal meshing (N·m-1) | |
1st stage | 4.8×108 | 8.0×108 |
2nd stage | 6.3×108 | 6.9×108 |
As shown in Fig. 11, the two-stage planetary gear system can be divided into five types of model according to the degree of discretization.
Model 1 is the traditional lumped mass model, which has 12 nodes. Model 2 takes the flexibility of shaft segment into account, and it is the primary model based on the shafting element method. Furthermore, model 3 considers the flexibility of the planet carrier on the basis of model 2. Similarly, model 4 considers the flexibility of gear ring based on model 2. Model 5 is a complete model of shafting elements, which fully considers the flexibility of different components. The whole system is divided into five shafting elements according to its structural characteristics, including the simple input shafting element, the special shafting element of the 1st ring, the intermediate shafting element of the planet carrier, the special shafting element of the 2nd ring, and the output shafting element of the planet carrier. The gear meshing elements coupled all the shafting elements to form the overall system model of which there are totally 113 nodes.
Table 3Bearing stiffness
Shaft bearing (N·m-1) | Input shaft | 5.0×107 |
Output shaft | 5.0×107 | |
Planet bearing (N·m-1) | 1st stage | 5.0×107 |
2nd stage | 5.0×107 |
Fig. 103D model of two-stage planetary gear system

Fig. 11The simplified model of two-stage planetary gear system
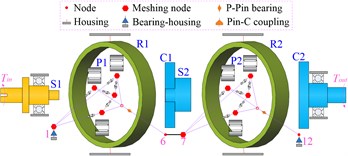
a) Model 1: lumped mass model
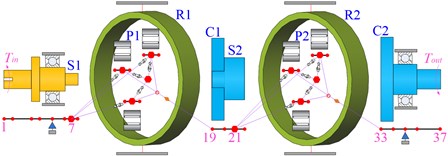
b) Model 2: considering flexibility of shaft segment
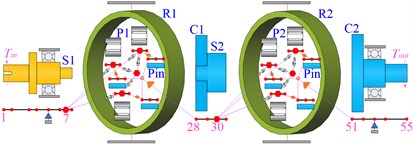
c) Model 3: considering flexibility of planet carrier
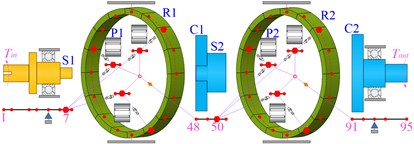
d) Model 4: considering flexibility of ring gear
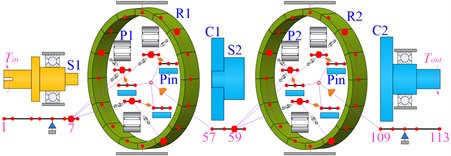
e) Model 5: complete model based on shafting element
3.2. Natural frequencies and vibration modes
Inherent characteristic is the inherent property of multiple-degree-of-freedom system [23]. The free vibration equation of the system can be expressed as Eq. (11) without taking the damping into account:
The corresponding eigenvalue problem is shown in the following equation:
where is order nonzero vector, which reflects the vibration modes, is vibration angular frequency, and is the corresponding natural frequency.
In each planet stage, the free vibration of the time-invariant representation is considered. The planets are assumed identical and equally spaced. All planet bearing stiffness’s are equal, all sun-planet mesh stiffness’s are equal, and all ring-planet mesh stiffness’s are equal. The carrier speed is assumed to be small and the gyroscopic terms is neglected. Then the natural frequency of the 5 types of models are obtained as Table 4.
In Table 4, the shadow represents that the multiplicity of natural frequency is 2, which can be denoted as . The natural frequencies solved by model 2 are the same with or smaller than model 1. This suggests that the natural frequency may reduce slightly after considering the flexibility of the shaft segment. Furthermore, the result solved by model 3 has a slight difference with model 1 and model 2, and the orders with basically have no change. Compared with model 1 to 3, the number of orders with reduced greatly solved by model 4. What’s more, the natural frequencies of each order have a much greater difference between model 4 and the first 3 models. The comparison results demonstrate that the ring gear flexibility has a more significant influence on the natural frequencies of the system than the planet carrier flexibility. In addition, the result of model 5 is relatively close to that of model 4. This can also help to prove the above conclusion.
Table 4Comparison of natural frequency of different models
Order | Natural frequency (Hz) | ||||
Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | |
1 | 14.5 | 14.5 | 14.3 | 14.5 | 14.3 |
2 | 15.2 | 15.2 | 15.1 | 15.2 | 15.1 |
3 | 15.2 | 15.2 | 15.1 | 15.2 | 15.1 |
4 | 22.4 | 22.4 | 22.4 | 22.4 | 22.4 |
5 | 239.1 | 238.8 | 229.4 | 227.5 | 219.3 |
6 | 239.1 | 238.8 | 229.4 | 235.2 | 226.2 |
7 | 375.5 | 356.1 | 343.1 | 353.1 | 340.5 |
8 | 408.0 | 407.7 | 394.7 | 377.6 | 366.3 |
9 | 408.0 | 407.7 | 394.7 | 397.8 | 385.5 |
10 | 595.1 | 595.0 | 566.7 | 552.3 | 552.3 |
11 | 620.0 | 620.0 | 606.7 | 552.3 | 552.3 |
12 | 620.0 | 620.0 | 606.7 | 593.2 | 565.2 |
13 | 636.9 | 636.9 | 620.0 | 636.9 | 606.7 |
14 | 636.9 | 636.9 | 620.0 | 636.9 | 606.7 |
15 | 696.4 | 696.1 | 670.0 | 657.3 | 639.0 |
16 | 696.4 | 696.1 | 670.0 | 671.3 | 651.2 |
17 | 819.3 | 819.0 | 780.4 | 775.3 | 745.0 |
18 | 819.3 | 819.0 | 800.5 | 775.5 | 753.1 |
19 | 826.3 | 826.2 | 800.5 | 826.2 | 780.4 |
20 | 920.2 | 913.3 | 896.8 | 873.2 | 857.7 |
21 | 1095.4 | 1094.8 | 1080.8 | 988.3 | 974.2 |
22 | 1095.4 | 1094.8 | 1080.8 | 1041.7 | 1026.2 |
23 | 1272.2 | 1257.1 | 1243.7 | 1197.3 | 1184.0 |
24 | 1455.2 | 1436.4 | 1426.4 | 1418.5 | 1407.1 |
25 | 1455.2 | 1436.4 | 1426.4 | 1430.3 | 1419.8 |
Several distinct types of vibration mode are summarized, such as planet torsional mode, sun-gear shaft axial mode, ring-gear axial mode and so on, as shown in Fig. 12. The natural frequency and vibration modes of model 5 are shown in Table 5.
Table 5Natural frequency and vibration modes of model 5
Vibration mode | Multiplicity | Natural frequency (Hz) |
Overall torsional mode (Fig. 12(a)) | 340.5/857.7/1184.0 | |
Planet torsional mode (Fig. 12(b)) | 219.3/226.2/366.3/385.5/5656.2/639.0/651.2/ 745.0753.1/974.2/1026.2/1407.1/1419.8 | |
15.1 | ||
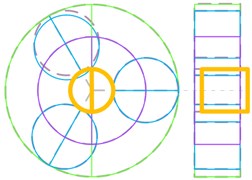
Sun-gear shaft axial mode (Fig. 12(c)) | 22.4 | |
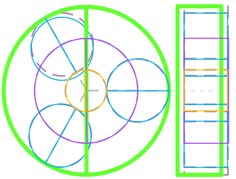
Ring-gear axial mode (Fig. 12(d)) | 552.3 | |
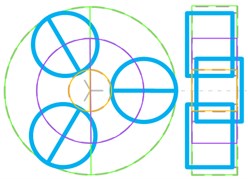
Planet axial mode (Fig. 12(e)) | 606.7 | |
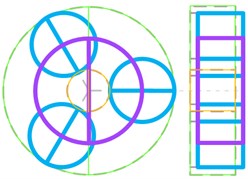
Planet + planet carrier axial mode (Fig. 12(f)) | 14.3/780.4 |
In Fig. 12, the dashed lines represent the non-vibration state of each component. Orange solid line represents the sun gear, and green solid line represents the ring gear, and blue solid line represents the planet gear, and purple solid line represents the planet carrier. The axial vibration modes are illustrated with the right-side view.
Fig. 12Classify of vibration modes
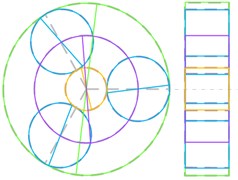
a)
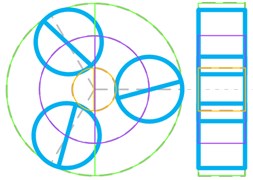
b)
c)
d)
e)
f)
4. Study of parameter sensitivity
4.1. Sensitivity to mesh stiffness
The normal synthetic mesh stiffness of gears can be solved using the Ishikawa equation [24]. Take the external meshing for instance, and denote the sun-planet mesh stiffness of the 1st stage and the 2nd stage planetary gear system, respectively. The curves of the time-varying mesh stiffness are shown in Fig. 13. The variation of one mesh stiffness is considered within a range between the maximum and minimum values in a mesh period, while the others are assumed as constant mean value. The sensitivity of natural frequencies to mesh stiffness is shown in Fig. 14.
As shown in Fig. 14, the mesh stiffness of the 1st stage has more important effect on the 24th and 25th order natural frequencies than the other orders, and to a lesser extent, the 27th and 28th orders are also influenced. However, the four orders are all planet torsional vibration mode of the 1st stage of the planetary gear system. In the meanwhile, the mesh stiffness of the 2nd stage has little influence on all the natural frequencies. But in the zoomed view, it is obvious that the 8th and 9th orders, and the 21st and 22nd orders are influenced at a certain extent. In addition, the four orders are all planet torsional vibration mode of the 2nd stage of the planetary gear system. In general, the change of mesh stiffness in the time varying range has little influence on the natural frequencies, and it mainly affects the planet torsional vibration mode of the corresponding stage of planetary gear system to different degrees.
Fig. 13Time-varying mesh stiffness
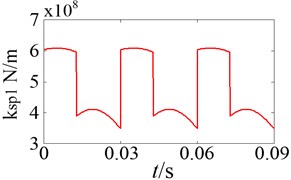
a) The 1st stage
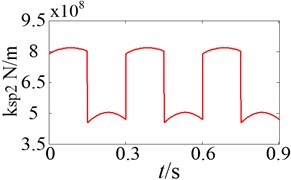
b) The 2nd stage
Fig. 14Change of natural frequencies influenced by different mesh stiffness
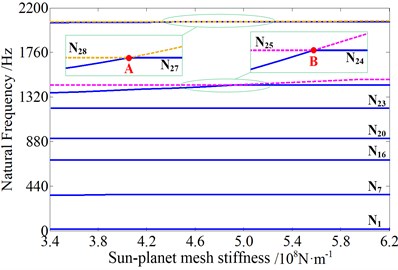
a) The 1st stage
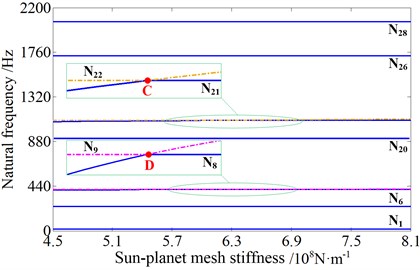
b) The 2nd stage
It can be observed that veering phenomena (A, B, C and D) occur when two planet torsional mode frequency loci approach each other, but then abruptly veer away. And the phenomenon occurs when the stiffness is approximately equal to the mean value. It just goes to show that multiple meshing pairs of the same stage taking the same mesh stiffness is the cause of for the number of planets is 3.
4.2. Sensitivity to bearing stiffness
The bearing stiffness is assumed to change within the range of 1×107-9×107 N·m-1. The sensitivity of natural frequencies to bearing stiffness of input/output shaft is shown in Fig. 15. The sensitivity of natural frequencies to planet bearing stiffness of the 1st/2nd stage is shown in Fig. 16.
Fig. 15 shows that the change of bearing stiffness of input shaft has evident effect on the sun-gear shaft axial vibration mode dominated by the 1st stage and the planet torsional vibration mode dominated by two stages together. Besides, the change of bearing stiffness of output shaft mainly affects the planet and planet carrier axial vibration mode dominated by the 2nd stage and the planet torsional vibration mode dominated by two stages together. It can be concluded that the variation of bearing stiffness of the input/output shaft not only affects the vibration modes of the adjacent stage of the planetary gear system, but also affects the nonadjacent stage. Moreover, it can be observed that the loci veering phenomena occur at A-Q points similar to what is shown in Fig. 14.
Fig. 16 shows that the change of planet bearing stiffness of the 1st stage can make significant effects on the planet torsional vibration mode, the planet axial vibration mode, and the planet and planet carrier axial vibration mode dominated by the 1st stage, and the planet torsional vibration mode dominated by the 2nd stage. Besides, the change of planet bearing stiffness of the 2nd stage does a relatively obvious influence on the planet torsional vibration mode dominated by the 2nd stage, and the overall torsional vibration mode dominated by two stages together. All the results mentioned above demonstrate that the variation of planet bearing stiffness of the 1st/2nd stage not only affects the vibration modes of its corresponding stage of the planetary gear system, but also affects other stages. Furthermore, the variation of radial bearing stiffness will also do effect on axial and torsional vibration modes. And the results demonstrate the coupling characteristics of the system under the free vibration condition. However, this is not in accord with the conclusion of existing literature. According to the author’s knowledge, this issue is worth continuing to explore, and the research in this area should get more attention. Moreover, it can also be observed that the loci veering phenomena occur similar to what is shown in Fig. 14 and Fig. 15.
Fig. 15The influence of bearing stiffness of input/output shaft on natural frequencies: ◆ – sun-gear shaft axial mode dominated by the 1st stage, ▲ – planet torsional mode dominated by two stages together, ☆ – planet and planet carrier axial mode dominated by the 2nd stage
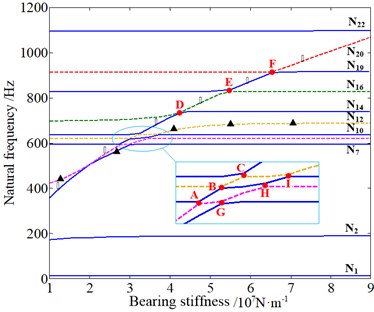
a) Input shaft
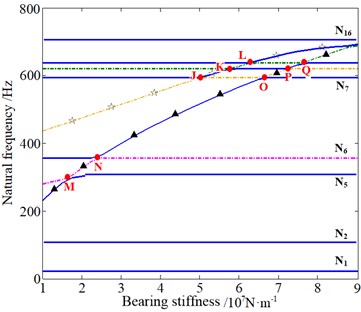
b) Output shaft
Fig. 16The influence of planet bearing stiffness of the 1st/2nd stage on natural frequencies: ◇ – planet torsional mode dominated by the 2nd stage, ▲ – planet torsional mode dominated by the 1st stage, ☆ – planet and planet carrier axial mode dominated by the 1st stage, ■ – planet axial mode dominated by the 1st stage, × – overall torsional mode dominated by two stages together
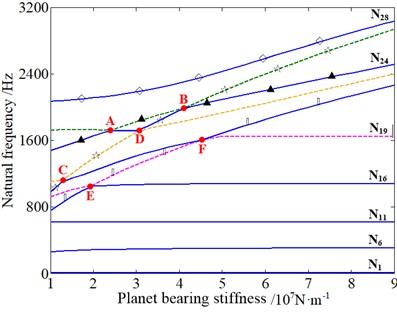
a) The 1st stage
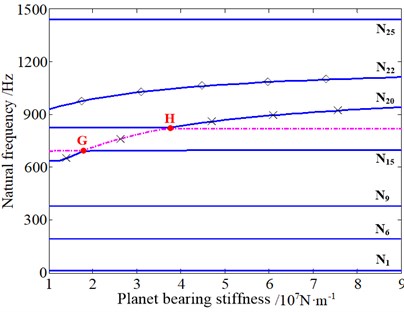
b) The 2nd stage
4.3. Sensitivity to mass of different structures
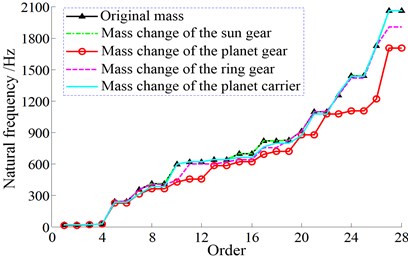
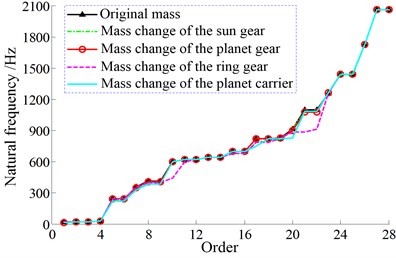
The sun gear, planet gear, ring gear, and planet carrier are the key components in a planetary gear transmission system besides the coupling shaft segments and bearings. Assumed that the mass of each structure is doubled, and then the change of the natural frequencies of the system is shown in Fig. 17.
As shown in Fig. 17, in the 1st stage, the curves of the mass changes of the sun gear and the planet carrier are basically coincident with that of the original mass. And the mass change of the ring gear appears to have a small impact on partial orders, such as the 10th and 28th order. And the mass increase of the planet gear has no effect on the first few natural frequencies, but it makes the higher order natural frequencies become lower obviously. In the 2nd stage, only the mass change of the ring gear causes a relatively great effect on partial orders, such as the 10th and 21st order. And the rest structures almost have no effect on the natural frequencies. In addition, similarly to the variation of mesh stiffness and bearing stiffness, the mass changes of different structures do not change the fundamental frequency of the system as well.
Fig. 17Natural frequency affected by mass changes of different structures
a) The 1st stage
b) The 2nd stage
5. Conclusions
In this study, the coupled lateral-torsional-axial dynamical model of the planetary gear system is established using the shafting element method. The mode characteristics and the parameter sensitivity are studied, and the specific conclusions are:
1) The ring-gear flexibility has a larger effect than other flexible effects on natural frequency. And almost all natural frequencies are distinct because of the loss of complete structural cycle-symmetry.
2) Distinct types of vibration mode are summarized, such as overall torsional mode, planet torsional mode, and even several axial modes though this is a spur gear system.
3) The variation of bearing stiffness of the input/output shaft not only affects the vibration modes of adjacent stage, but also affects the nonadjacent stage. The variation of planet bearing stiffness not only affects the vibration modes of its corresponding stage, but also affects other stages. The variation of radial bearing stiffness will also do effect on axial and torsional vibration modes. And the results demonstrate the coupling characteristics of the system under the free vibration condition. However, this is not the same with the conclusion of existing literatures.
References
-
Derek S. J. Gear Noise and Vibration. Second Edition, Marcel Dekker, 2003.
-
Cunliffe F., Smith J. D., Welbourn D. B. Dynamic tooth loads in epicyclic gears. Journal of Engineering for Industry, Vol. 96, Issue 2, 1974, p. 578-584.
-
Botman M. Epicyclic gear vibrations. Journal of Engineering for Industry, Vol. 98, Issue 3, 1976, p. 811-815.
-
Lin J., Parker R. G. Analytical characterization of the unique properties of planetary gear free vibration. Journal of Vibration and Acoustics, Vol. 121, Issue 3, 1999, p. 316-321.
-
Lin J., Parker R. G. Structured vibration characteristics of planetary gears with unequally spaced planets. Journal of Sound and Vibration, Vol. 233, Issue 5, 2000, p. 921-928.
-
Wang S., Song y., Zhang C., Xu W. Impacts of basic parameters on planetary gear characteristics. China Mechanical Engineering, 2005, p. 615-618.
-
Zhang J., Song Y., Zhang C., et al. Analysis of free vibration of NGW spur planetary gear set. Journal of Tianjin University, Vol. 11, Issue 1, 2010, p. 90-94.
-
Kahraman A. Free torsional vibration characteristics of compound planetary gear sets. Mechanism and Machine Theory, Vol. 36, 2001, p. 953-971.
-
Kiracofe D., Parker R. G. Structured vibration modes of general compound planetary gear systems. Journal of Vibration and Acoustics, Vol. 129, 2007, p. 1-16.
-
Lin J., Parker R. G. Sensitivity of planetary gear natural frequencies and vibration modes to model parameters. Journal of Sound and Vibration, Vol. 228, Issue 1, 1999, p. 109-128.
-
Guo Y. C., Parker R. G. Sensitivity of general compound planetary gear natural frequencies and vibration modes to model parameters. Journal of Vibration Acoustics, Vol. 132, Issue 1, 2010, p. 655-672.
-
Hua X., Lim T. C., Peng T., et al. Dynamic analysis of spiral bevel geared rotor systems applying finite elements and enhanced lumped parameters. International Journal of Automotive Technology, Vol. 13, Issue 1, 2012, p. 97-107.
-
Young Y. L. Dynamic hydroelastic scaling of self-adaptive composite marine rotors. Composite Structures, Vol. 92, Issue 1, 2010, p. 97-106.
-
Lin C. H., Tsao T. P. Depressing the torque vibrations of turbine blades using virtual inertia. Electric Power Systems Research, Vol. 61, Issue 1, 2002, p. 23-32.
-
Huebner K. H., Thornton E. A. The Finite Element Method for Engineers. 4th Edition, John Wiley & Sons, 2001.
-
Vosoughi A. R. A developed hybrid method for crack identification of beams. Smart Structures and Systems, Vol. 16, Issue 3, 2015, p. 401-414.
-
Helsen J., Vanhollebeke F., Marrant B., et al. Multibody modelling of varying complexity for modal behaviour analysis of wind turbine gearboxes. Renewable Energy, Vol. 36, Issue 11, 2011, p. 3098-3113.
-
Zhu C., Xu X., Liu H., et al. Research on dynamical characteristics of wind turbine gearboxes with flexible pins. Renewable Energy, Vol. 68, 2014, p. 724-732.
-
Qin D., Wang J., Lim T. C. Flexible multibody dynamic modeling of a horizontal wind turbine drivetrain system. Journal of Mechanical Design, Vol. 131, 2009, p. 1-8.
-
Chen Z., Zhu Z., Shao Y. Fault feature analysis of planetary gear system with tooth root crack and flexible ring gear rim. Engineering Failure Analysis, Vol. 49, 2015, p. 92-103.
-
Liu C., Qin D., T.C. Lim., et al. Dynamic characteristics of the herringbone planetary gear set during the variable speed process. Journal of Sound and Vibration, Vol. 333, Issue 24, 2014, p. 6498-6515.
-
Liu C., Qin D., Liao Y. Dynamic model of variable speed process for herringbone gears including friction calculated by variable friction coefficient. Journal of Mechanical Design, Vol. 136, Issue 4, 2014, p. 1-12.
-
Sun W., Ding X., Wei J., et al. A method for analyzing sensitivity of multi-stage planetary gear coupled modes to modal parameters. Journal of Vibroengineering, Vol. 17, Issue 6, 2015, p. 3133-3146.
-
Shi J., Ma X., Xu C., et al. Meshing stiffness analysis of gear using the Ishikawa method. Applied Mechanics and Materials, 2013, p. 203-206.
Cited by
About this article
The research was supported by the National Basic Research Program of China (2014CB046304). The authors would also like to acknowledge the support from the Fundamental Research Funds for Central Universities (106112015CDJXY110001).
