The Influence of projectile shielding on the internal magnetic field during an electromagnetic launch

2.1. Mathematical model of the magnetic field environment for an electromagnetic railgun

The principle of the electromagnetic railgun is shown in Fig. 1. The pulse current flows in the rail and the armature, which produces a high magnetic field in the bore and generates the Lorentz force to propel the armature [17]. The nonlinear effects of rail erosion caused by high-speed movement between armature and rails are ignored in this paper.

Fig. 1Working principle diagram of an electromagnetic railgun [16].

The pulse current flows along the opposite direction at both sides of the rail, and the current distribution in the rail is subjected to the skin effect. Considering the current model of an electromagnetic railgun, it is assumed that the rail current is only distributed at the skin depth $\delta$ of each surface and is evenly distributed at the skin depth:

where $\delta$ is the skin depth; $f$ is the frequency of the current; and $\sigma$ and $\mu$ are the conductivity and permeability of the conductor, respectively.

Since the calibre and length of the electromagnetic railgun are far shorter than the wavelength of the electromagnetic field, the displacement current can be ignored. The railgun can be considered a quasi-static system [18]. Combined with the differential form of Maxwell’s equations and Ohm’s law, the magnetic diffusion equation during electromagnetic launch can be obtained as follows [19]:

where $B_z$ is the magnetic induction in the $z$-direction, $\sigma$ is the conductivity of the rail, ${\mu }_0$ is the vacuum permeability, and $v_x$ is the velocity diffusion term.

For the rails, there is an $x$-direction reverse velocity relative to the armature, and $v_x$ is negative. Since the armature is assumed to be stationary, $v_x=$0, and the magnetic diffusion equation in the armature region can be expressed as:

where $\sigma$ is the conductivity of the armature.

Furthermore, by solving the magnetic diffusion equation of the rails and armature, their current densities can be obtained by using Ampere’s law:

where $j_x$ is the $x$-direction component of the current density, $j_y$ is the $y$-direction component of the current density.

Since the input current of the electromagnetic railgun is a low-frequency pulse current, the magnetic field generated is similar to a steady magnetic field:

where $V$ is the body current distribution area, $r´$ is the vector diameter of the source point, $r$ is the vector diameter of the field point. The main parameters affecting the test point are the spatial position of the test point from the source point and the current density component of the source point.

2.2. Calculation model of magnetic induction for the armature and rails

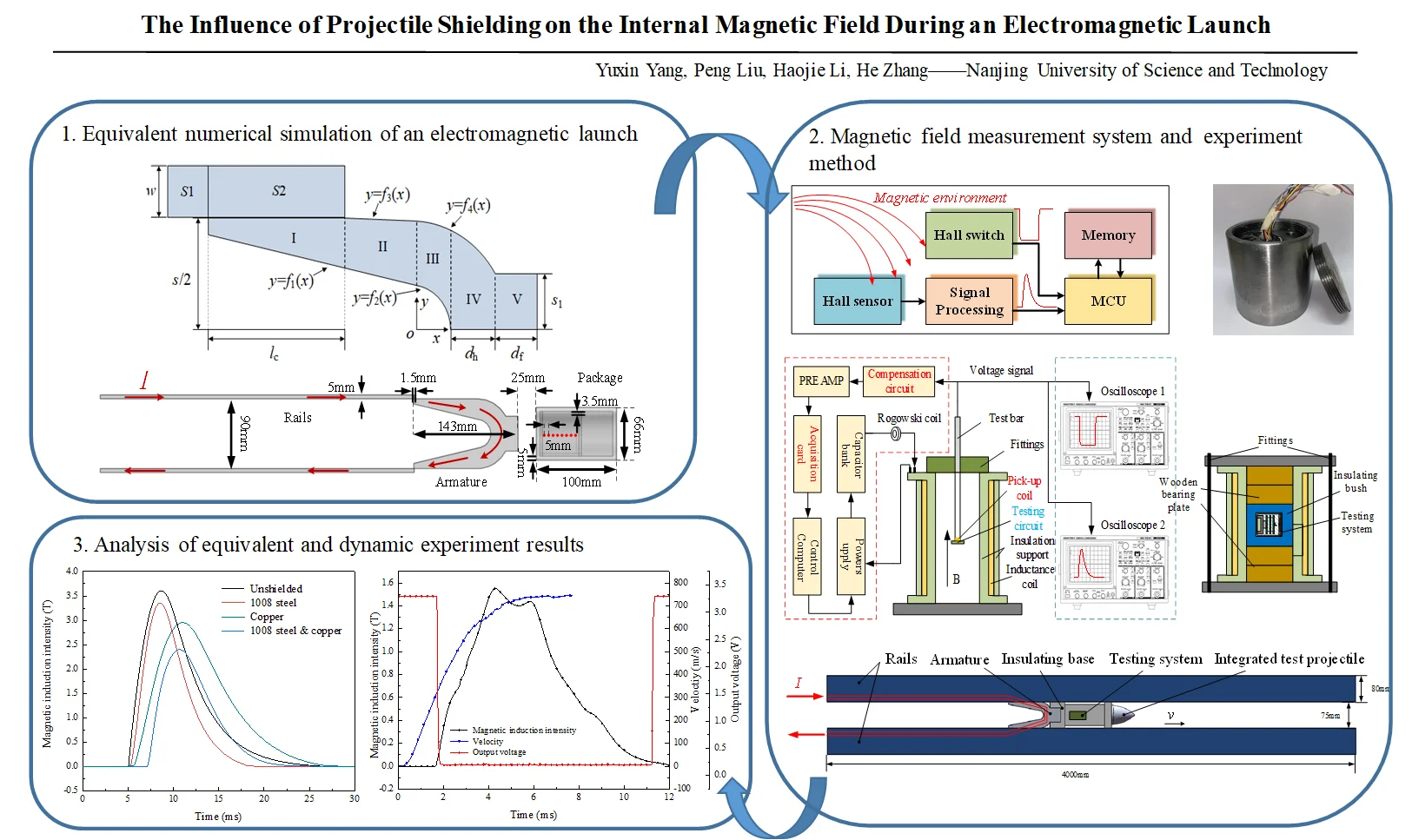
In this section, a C-type armature, which is the most common solid armature, is used for research [20]. Considering the diffusion effect of the current in the armature, the halved C-type armature is divided into five regions for calculation as shown in Fig. 2, where $y=f_1\left(x\right)$, $y=f_2\left(x\right)$, $y=f_3\left(x\right)$ and $y=f_4\left(x\right)$ represent the curve equations obtained by projection on the $xy$-plane of the inner surface of the trailing edge, the curvature circle, the tail arm and the outer surface of the throat, respectively. The width of the rail is $w$. The calibre of the railgun is $s$. The length of contact line between armature and rail is $l_c$. The top surface of armature is $s_1$. The length of armature in IV and V is $d_h$ and $d_f$, respectively. The average current densities $J_{vx}$ and $J_{vy}$ in each region are obtained by using the magnetic diffusion equation. In each region, the flux density of the observation point is calculated by using the current element model. Finally, vector addition is carried out to obtain the magnetic flux density of the whole armature at the observation point.

Fig. 2Calculation model of the C-type armature

It is assumed that the rail current is only distributed on each surface, and the skin depth $\delta$ is evenly distributed. The current distributions on the upper and lower surfaces of the rail and armature are the same, while the current distribution coefficients on the inner and outer surfaces are $f_1$ and $f_2$, respectively, where $f_1>f_2$, and $f_1+f_2=2$ [21]. The current of rail surface S1 is:

where $h_r$ and $w$ are the height and depth of the rail, respectively.

S1 is regarded as a thin current-carrying plate, and the current density is:

The distance $R$ from the source point to the field point is equal to:

The source point coordinates are $\left(x,y,z\right)$. According to Eq. (5), the generated magnetic flux density is:

The expression of the $z$-direction flux density $B_{vz1}$ produced by surface S1 is:

The expression of the flux density $B_{vy1}$ along the $y$-direction is:

Armature region I in Fig. 2 represents the contact region between the rail and the trailing edge of the armature. $x$ varies within [$-l_t$, $-l_t+l_c$], while $y$ is within [$f_1\left(x\right)$, $s$/2]. It is assumed that the current densities of region I along the $x$- and $y$-directions are $J_{ax1}$ and $J_{ay1}$, respectively. Then, the expression of the $z$-direction magnetic flux density $B_{axz1}$ is:

The expression of the generated flux density $B_{axy1}$ along the y-direction is:

The expression of the $z$-direction flux density $B_{ayz1}$ generated by the $y$-direction current of region I at the observation point is:

The x-direction flux density $B_{ayx1}$ is expressed as:

Similarly, the flux densities of other regions can be obtained. The value range of each area is shown in Table 1.

Table 1 also presents the value range of contact area S2. In fact, when the armature is moving, the current density flowing through area S2 can be ignored; when the armature is static, the current in area S2 can also be decomposed into $x$- and $y$-direction currents. The calculation method of magnetic flux density generated at the observation point applies to each area of the armature.

3.1. Equivalent simulation model

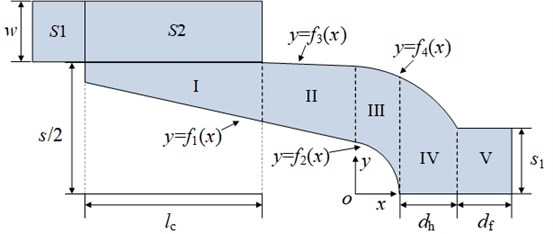
Based on the mathematical model, an equivalent model of an electromagnetic railgun is shown in Fig. 3. The rails are made of copper alloy, with a conductivity of 1.8×10⁷S/m. The armature is made of aluminium alloy, with a conductivity of 2.4×10⁷ S/m. The effect of the velocity skin effect on the contact interface between armature and rails is considered in the proposed model. During launch, the armature moves at a high speed relative to the rails. The current distributions in the rail and the armature change significantly at the same time. The current is mostly concentrated on the rail surface (10 % of the rail width) and partially on the trailing edge of the armature (2 % of the armature length) [22]. When the current enters the armature, the current distribution in the dynamic armature is the same as that in the static armature. Therefore, here, the contact model between the rails and the armature is simplified. The width of the rail is 5 mm and the contact area between the rails and the armature is 1.5 mm.

Fig. 3Equivalent model of an electromagnetic railgun during launch

The outer and inner packages are equivalent to projectile shielding and control circuit shielding, respectively. The thicknesses of the inner and outer packages are 3.5 mm and 5 mm, respectively. The inspection points are set from 32 mm to 62 mm away from the central axis of the armature, and one inspection point is set every 5 mm.

3.2. Distribution of magnetic induction in front of the armature

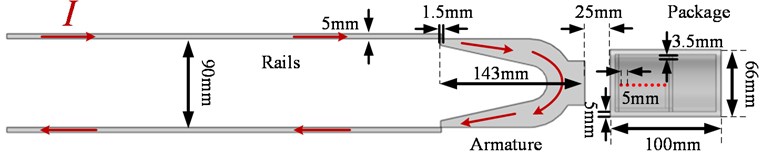
The input current of an electromagnetic railgun is provided by one or more capacitor banks. In this paper, a single capacitor bank is used to study the distribution of magnetic induction in the time-varying phase of the current rising and falling. The input current is divided into two phases. In the first phase (5-8 ms), the current increases gradually to the peak (5.5 MA); in the second phase (8-23 ms), the current decreases gradually from the peak.

The current in Fig. 4 is used in the simulation model to calculate the magnetic induction. The projectile shielding and control circuit shielding are set as non-metallic materials to investigate the internal magnetic field distribution without shielding. The simulation results are shown in Fig. 5(a). Each plot has the same trend, but the amplitude is different. The maximum and minimum peak values are 3.8 T and 2.4 T, respectively. As the distance between inspection point and armature increases, the magnetic induction decreases, as shown in Fig. 5(b). The results suggest that there is a relatively high magnetic field near the armature. The magnetic field near the armature has obvious characteristics and can be used as an environmental signal for control circuit.

Fig. 4Input current

Fig. 5Simulation of magnetic induction at different distances in front of the armature

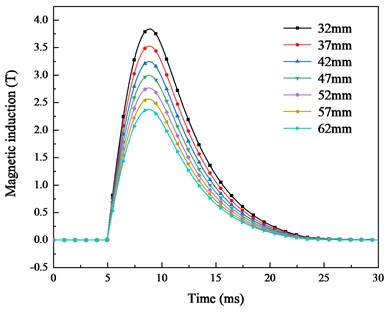
a) Magnetic induction at different points

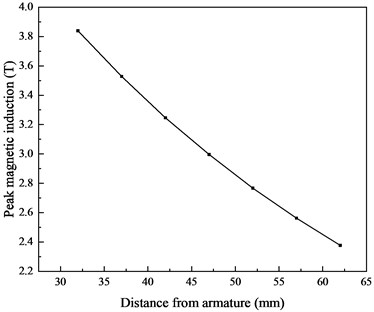
b) Peak magnetic induction

3.3. Analysis of the influence of the shielding material on magnetic induction

In Section 3.2, the magnetic induction of the projectile position was analysed. The simulation results showed that it is mainly affected by the input current and the distance from the armature. However, the influence of projectile material is not considered. The protection of the ammunition and control circuit is vital to safety during launch. The projectile is mainly composed of metal materials, which have different responses to magnetic fields. For materials with good conductivity, eddy current cancellation serves as their shielding mechanism. According to Faraday’s law, the eddy current effect is produced on the surface of the material to provide a reverse magnetic field; moreover, most of the magnetic field is transmitted by ferromagnetic materials. Flux diversion occurs, and the magnetic field density in the cavity is low.

Previous studies have most often discussed the effects of conductive and magnetic materials on the steady magnetic field, where the amplitude of magnetic induction is the primary concern. But for a pulsed magnetic field during launch, the amplitude, change time and duration are all worthy of attention. This section mainly studies the variation of magnetic induction at each point under different shielding materials, such as single permeability magnetic material, single conductive material and composite material.

The peak magnetic induction is compared with the shielding effectiveness (SE) equation:

where $B_{wo}$ and $B_w$ are the magnetic inductions of the observation point before and after shielding, respectively. In this paper, the shielding effectiveness is expressed as the peak magnetic induction due to the transient magnetic field during electromagnetic launch.

3.3.1. Simulation of a single-layer magnetic material

Low carbon 1008 steel and mumetal are used for the simulation, and the B-H curves are shown in Fig. 6(a). The input current is consistent with that in Fig. 3(a). For convenience, the 32 mm point is selected for comparison. These two packaging materials have little influence on the distribution of internal magnetic induction, as shown in Fig. 6(b). In contrast, low carbon steel has a greater influence on the internal magnetic induction. The peak shielding efficiency of 1008 steel is 0.35 dB, and the mumetal only has a peak shielding efficiency of 0.09 dB.

Fig. 6Comparison of the magnetic induction with and without the influence of the magnetic material

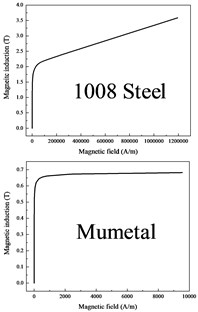
a) B-H curve of the two materials

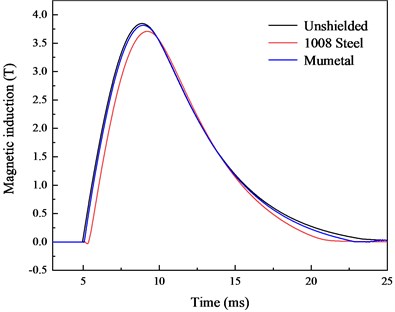
b) Simulation of the magnetic induction

Fig. 6(b) suggests that the start time when using 1008 steel is 0.39 ms slower than that of the unshielded condition. According to the shielding principle of the magnetic material, the magnetic material acts as the magnetic circuit in the magnetic field. Most of the magnetic field is transmitted by the magnetic material, so that 1008 steel has a good shielding effect at the initial 0.39 ms. However, when the external magnetic field is enhanced, the magnetic material reaches saturation, and there is no better performance in the subsequent time. Therefore, the influence of the magnetic material on the internal magnetic field can be ignored when the inspection point is close to the armature.

3.3.2. Simulation of a single-layer conductive material

Copper and aluminium are used for the simulation in this section, and the conductivities are shown in Fig. 7(a). The magnetic induction of the investigated points is compared, as shown in Fig. 7(b). It can be found that conductive material shielding has a better effect than the unshielded method. The peak magnetic induction of the copper material is reduced by 20 %, and the peak shielding efficiency reaches 1.94 dB. The peak magnetic induction of the aluminium material is reduced by 12 %, and the peak shielding efficiency reaches 1.05 dB.

Conductive materials have better shielding effect in high magnetic field environment. When the external magnetic field is enhanced, the induced current will be generated outside the conductive material. The higher conductivity of the shielding material, the larger the induced current. A reverse magnetic induction is formed to counteract part of the external magnetic field. As the eddy current magnetic field lags behind the original magnetic field, the peak magnetic field is delayed.

Fig. 7Comparison of magnetic induction with and without the influence of the conductive material

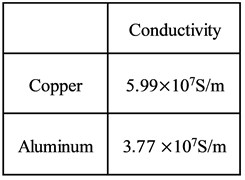
a) Conductivity of the materials

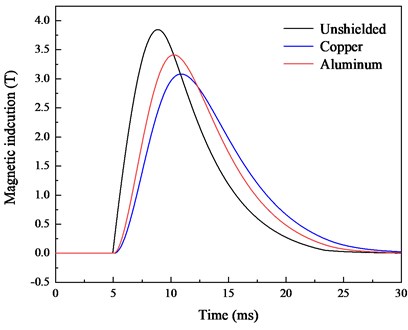
b) Simulation of the magnetic induction

3.3.4. Comparison of different shielding methods

The simulation results are shown in Table 2. The peak magnetic induction, shielding effectiveness, change time and duration are compared. The change time, expressed as the moment of magnetic induction, rises from zero and drops to zero.

Fig. 8Comparison of the magnetic induction with and without the influence of the double layer material

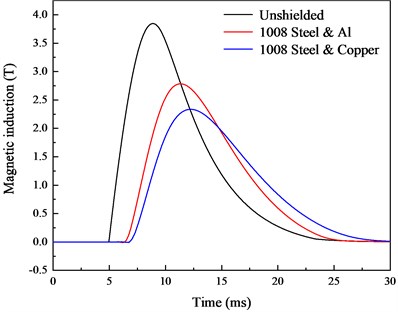
a) 1008 steel and conductive material

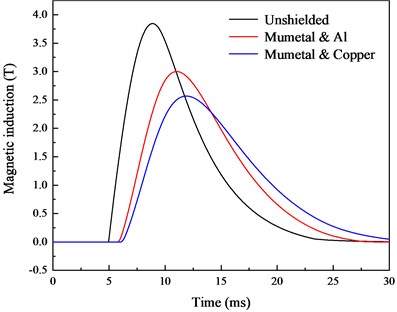
b) Mumetal and conductive material

As suggested, the shielding method of magnetic materials mainly affects the change time and duration of magnetic induction. The start time is later with shielding than without, with a maximum delay of 0.39 ms; the end time is earlier with shielding than without, ending at most 3.9 ms earlier. The duration under magnetic permeability shielding is shorter than that of the unshielded method. Specifically, the 1008 steel condition has a duration of 15.71 ms, while with mumetal, the duration is 17.20 ms. This is because part of the magnetic induction is channelled into the magnetic material and because the interior magnetic induction is lower and the pulse width is shorter.

Table 2Comparison of different shielding methods

Package materials	Peak magnetic induction (T)	SE (dB)	Change time (ms)	Duration (ms)
Unshielded	3.85	/	5.00/24.85	19.85
1008 steel	3.70	0.35	5.39/21.10	15.71
Mumetal	3.81	0.09	5.25/22.45	17.20
Copper	3.08	1.94	5.37/29.57	24.20
Aluminium	3.41	1.05	5.26/27.17	21.91
1008 steel & Al	2.78	2.83	6.52/25.45	18.93
1008 steel & copper	2.33	4.36	6.95/28.50	21.55
Mumetal & Al	3.01	2.14	5.93/26.82	20.89
Mumetal & copper	2.56	3.54	6.24/29.73	23.49

Conductive materials have better shielding effectiveness than magnetic materials. Compared to the unshielded condition, the start and end times with shielding occur later, with delays of, at most, 0.37 ms and 4.72 ms, respectively, which are due to the eddy current shielding effect of conductive materials. At the rising edge of the magnetic induction intensity, the eddy current effect of conductive shielding reverses magnetic induction, which counteracts the internal and external magnetic induction. The effect of the eddy current prevents the magnetic induction from decreasing in the decreasing stage, so, in the case of shielding with conductive materials, the initial and end stages are slower than those without shielding.

The composite shielding method is found to have a better shielding effect and can reduce the peak magnetic induction by approximately 38.9 %. At the same time, compared with other methods, its start time occurs after the unshielded method, with a maximum delay of 1.95 ms. The duration is longer for the composites than for the of unshielded condition, except the composite of 1008 steel and aluminium, which have a duration of 19 ms less. The composite shielding of copper and 1008 steel can achieve a better shielding effect, but with a serious lag in the start time and longer duration.

4.1. Magnetic measurement system

The working principle of the magnetic measurement system is shown in Fig. 9. A Hall switch and linear Hall sensor are used for the test of the pulsed high magnetic field.

Fig. 9Working principle of the magnetic measurement system

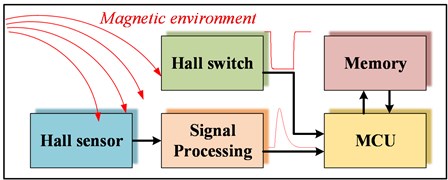
Fig. 10Principle of Hall switch-based magnetic environment detection

The output voltage of the linear Hall sensor is processed by the signal, and the output voltage at 3.5 T is adjusted to the maximum input voltage corresponding to the Analog-to-Digital converter (ADC) of microcontroller. The sensor signal matches the voltage ranging from 0 to 3.3 V through an appropriate circuit. The voltage is converted to an output signal with a frequency range of 40 kHz by using the ADC input and lookup table of the microcontroller. The output value of the Hall switch is converted to a low-level signal or a 3.3 V high-level signal. Hall switch A3144 and linear Hall CY106S were used as sensors, while C8051F was chosen as a microcontroller.

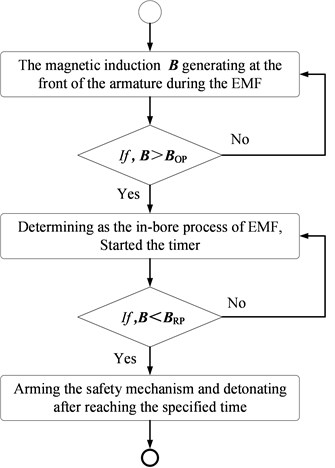
The flow chart in Fig. 10 shows how the Hall switch works. $B_{OP}$ and $B_{RP}$ are the operating and release point thresholds of the Hall switch, respectively. The output becomes “low” when the magnetic field at the Hall sensor exceeds the $B_{OP}$; when the magnetic field is reduced to a value below the $B_{RP}$, the device output becomes high.

4.2. Shielding experiment in a high magnetic field generator

The high magnetic field generator is composed of a pick-up coil, compensation circuit and acquisition card, as shown in Fig. 11. The induction electromotive force is generated by the pick-up coil, and the extra voltage of the pick-up coil is eliminated by the compensation coil. Finally, voltage acquisition and processing are completed by the acquisition card. The whole process of signal acquisition and processing is outlined by the dotted red line.

Fig. 11Working principle of the magnetic measurement system

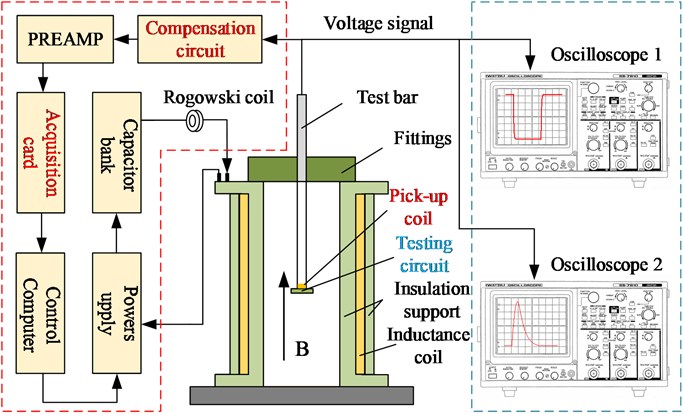
Testing and calibration of the testing circuit were performed at Wuhan National High Magnetic Field Center using a high magnetic field generator. Pulsed magnetic fields were generated by multiple winding coils with an aperture of 75 mm and a height of 228 mm. The pulses used for testing and calibration were half-period sinusoidal pulses with amplitudes up to 3.5 T. The pick-up coil equipped with an integrator was used to calibrate the magnetic field sensor. The pick-up coil was positioned in the centre of the coil at the same location as the projectile-borne storage testing system. To verify the stability and reliability of the testing system, the mapping relationship between the output voltage of the testing system and magnetic induction is studied by using Gaussian process regression.

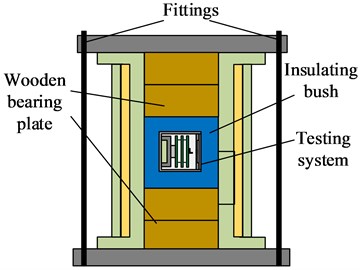
The same charging and discharging modules in Section 4.2 are also utilized in the shielding experiment. Except for the module for the real-time signal test, the magnetic field test circuit is packaged in the shielding material. The thicknesses of the shielding materials are 3.5 mm and 5 mm, which are the same as those in Section 3.1. As shown in Fig. 12, the wooden bearing plate, insulation bush and fittings are used to limit and fix the magnetic measurement system and make the test position of the magnetic field sensor the same as that of the pick-up coil. After the experiment, the upper computer is used to read back the data in the magnetic measurement system.

Fig. 12Measurement of SE with different materials

4.3. Shielding experiment during launch

A schematic diagram of an electromagnetic railgun is shown in Fig. 13(a), where the width, length and calibre of the rail are 80 mm, 4 m and 75 mm, respectively. The integrated test projectile and insulation support are fixed to the armature. The integrated projectile is composed of a projectile-borne storage testing system, a copper alloy package and an insulating sabot. The test device is shown in Fig. 13(b), which mainly consists of a control circuit, lithium battery and battery holder. The shielding of the test device is low carbon 1008 steel.

Fig. 13Experimental diagram of electromagnetic launch

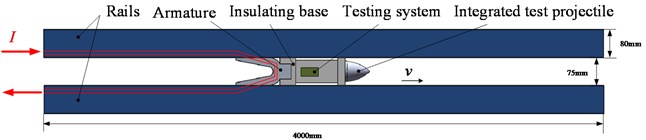
a) Schematic diagram of electromagnetic launch

b) Storage system

5.1. Measurement results of the pulsed magnetic field generator

The input current of the inductive coil and electromagnetic railgun is provided by a large capacitance discharge. Therefore, the discharge circuit is designed to simulate the distribution of in-bore magnetic induction during electromagnetic launch. The discharge experiment is carried out with a 1-MJ power supply, a charging voltage of 2 kV, and with the pick-up coil located in the centre of multiple winding coils. The input current is shown in Fig. 14(a).

The current starts to rise at 5.015 ms, reaches the peak value of 3376.6 A at 8.35 ms and then begins to decline. The current is just 28.4 A at 25 ms and drops to zero at 30 ms. The magnetic induction is basically consistent with the pulse current, as shown in Fig. 14(b). It rises from 4.7 ms to 8.35 ms, reaches the peak value of 3.60 T and then decreases gradually. The magnetic induction is close to zero at 25 ms. Therefore, multiple winding coils can be used to simulate the magnetic induction of the projectile position in the electromagnetic launching process.

Following the method given in Fig. 11, the magnetic induction and Hall switch signal readback are shown in Fig. 15. The red line represents the output voltage of the Hall switch, and the black line indicates the magnetic induction. When the magnetic induction changes ($t=$ 4.95 ms), the voltage signal decreases to 0.2 V in 0.1 ms and remains unchanged in the magnetic induction pulse width; when the magnetic induction decreases to nearly 0 T ($t=$ 24.45 ms), the voltage signal increases to 3.3 V in 0.1 ms. In this process, the Hall switch completes the measurement of the magnetic induction signal in multiple winding coils.

Fig. 14Measurement results of the pulsed high magnetic field generator

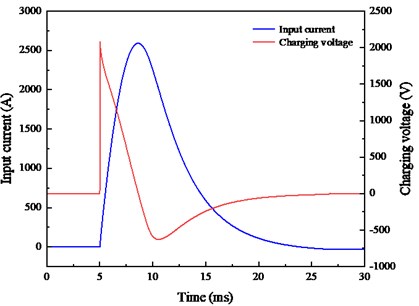
a) Input curve

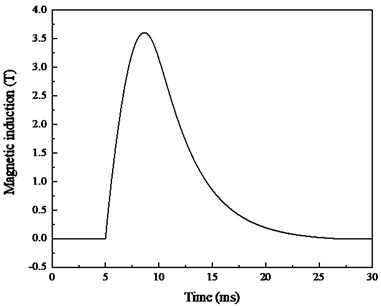
b) Output magnetic induction

Fig. 15Measurement results of magnetic induction and output voltage

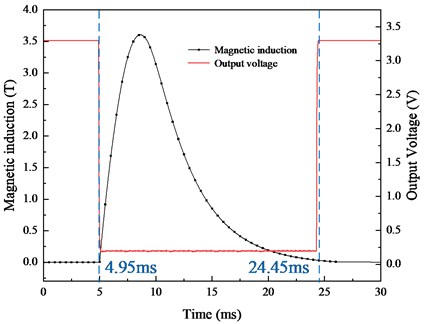
5.2. Experiment of shielding effectiveness with different materials

The same discharge voltage was used for the pulsed magnetic field experiment. Copper, low carbon 1008 steel and double layer shielding materials are chosen for the experiment. The experimental values of magnetic induction are shown in Fig. 16(a). As indicated, the composite of low carbon 1008 steel and copper have the lowest magnetic induction. The experimental value closely matches the simulation results presented in Section 3. Figs. 16(b)-(d) show comparisons between the internal magnetic induction and the output voltage signal of the Hall switch under different shielding materials. The duration of the measured magnetic induction under different shielding materials is consistent with the simulation results.

Fig. 16Comparison of magnetic induction and output voltage

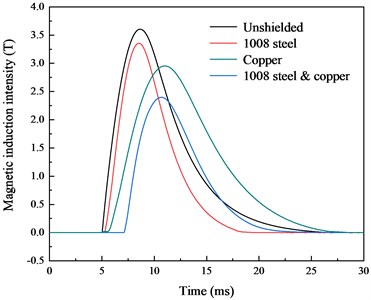
a) Comparison of magnetic induction

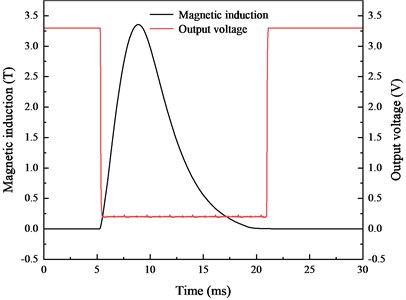
b) Low carbon 1008 steel

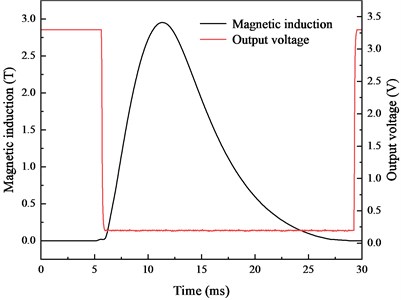
c) Copper

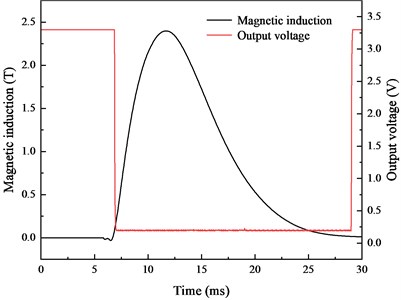
d) Low carbon 1008 steel and copper.

The change time of the Hall switch and the duration of magnetic induction are listed in Table 3. It can be found that different shielding materials exert different influences on the response time of the internal Hall switch. Compared with the unshielded experiment, the time errors of low carbon 1008 steel, copper and the composite of low carbon 1008 steel and copper are 18.97 %, 22.77 % and 12.82 %, respectively. Therefore, the magnetic and conductive materials affect the internal magnetic induction in the pulsed magnetic field environment, and the shielding effectiveness of composite shielding is the best, reaching 3.57 dB. Additionally, conductive and magnetic materials also affect the change time and pulse width of the pulsed magnetic field due to their shielding mechanisms.

5.3. Recovery considering the influence of projectile shielding during launch

The dynamic test current, which has a peak current of approximately 1 MA, is shown in Fig. 17(a). The distribution of the magnetic induction without considering the shielding material is shown in Fig. 17(b), which has a peak value of approximately 2 T.

Fig. 17Comparison of velocity, magnetic induction and output voltage of the Hall switch during launch

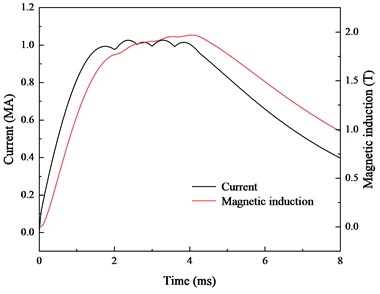
a) Input current and simulation magnetic induction

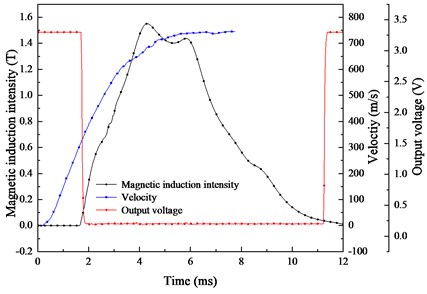
b) Measured data during launch

The results of the dynamic experiment are shown in Fig. 17(b). The blue curve is the velocity, which is integrated by the measured value of the acceleration sensor. The velocity changes within a time range of 0.15-7.8 ms, and the muzzle velocity is 750 m/s. The red curve is the Hall switch test value, and the black curve is the linear Hall sensor test value. This work uses envelopes of the analogue signal measured by the linear Hall sensor, which does not affect the analysis of the peak value and duration of the magnetic field. The magnetic induction curve begins to rise at 1.65 ms and decreases to 0 T at 12 ms. The peak magnetic induction is 1.55 T.

Without shielding, the trends of the simulated magnetic field and current are similar. Under the double shielding effect, the magnetic field clearly has a time delay, and the time error reaches 18 %. In further designs, this delay should be corrected.