Abstract
Natural gas produced in the Russian Federation is transported through main gas pipelines united into the Unified Gas Supply System of the Russian Federation. The system of main gas pipelines - the most important link in the unified gas supply system – is a large, complex and continuously developing technological system. Maximum internal pressure is one of the key characteristics for any pipeline. This indicator helps to set the limit for the capacity of the pipeline (maximum volume of pumped gas per unit of time), its level of reliability, as well as the level of hazard and potential risk (the higher the pressure inside the pipeline, the more potential threat it carries). In order to increase the reliability of determining the pressure in the gas pipeline, it is proposed to perform noise suppression using a wavelet transform in the work. Noise reduction in the wavelet transform is carried out due to the fact that the signal is decomposed into approximating and detailing coefficients. After removing the detailing component, the decomposition is restored and the output is a slightly distorted signal. Thus, when you remove an insignificant part of the original signal, the graphs of the change in values become more visual. This paper compares the efficiency of wavelet based thresholding techniques in the presence of noise for various wavelet family. For comparison, the trend processing was performed by two types of wavelets recommended for noise reduction - Symlet and Daubechies wavelets.
1. Introduction
When passing through the communication channel, a noise component is added to any signal. Depending on the origin of the noise, the signals are distinguished between acoustic, mechanical, electromagnetic, electrical and other noises. Also, noise is divided into white, color, white with limited bandwidth, impulsive, narrowband.
To eliminate noise, various noise reduction methods are applied to signals, including those based on mathematical transformation. The Fourier transforms, the windowed Fourier transform (FFT), and the Gabor transform are well known.
Wavelet transform is relatively new. Wavelet spectrograms are more informative than conventional Fourier spectrograms, and unlike the latter, they allow revealing the finest local features of acoustic signals.
Currently, this mathematical transformation is widely used as a signal processing and analysis method. Wavelet transform used in vibration-based diagnostics, in the processing of seismic sensor records in oil exploration for the localization of parts of different scales, in medicine in the processing of electrocardiograms and noise reduction in tomography [1-4].
With the windowed Fourier transformation, it is necessary to choose the type of window for analyzing the entire signal, and a narrow window will provide the best time resolution, and a wide one - frequency. The wavelet transform solves this problem. Although it is performed in the same way, the signal is multiplied with the wavelet in the same way as with the Short Time Fourier Transform with a window function.
The wavelet transform allows the use of large time intervals where more accurate information about the low frequency is needed, and shorter ones when information about the high frequency is needed.
2. Wavelet transform
With the development of the theory of wavelets, it becomes possible with high accuracy to represent the smallest features of functions, up to jumps, with their reference to time, making it possible to high-precision filtering.
Since wavelets localize functions at different scales, it becomes possible to preserve an important part of the signal by removing noise, which is very important in modern communication systems.
Due to its properties, the wavelet transform makes it possible to select the main “non-chaotic” noise from the “non-white” noise. Noise reduction (thresholding or wavelet denoising) is carried out due to the fact that the signal is decomposed into approximating and detailing coefficients. Approximating coefficients are large-value coefficients that concentrate the signal. Detail coefficients are small and usually represent noise that can be removed without affecting the main signal. After removing the detailing component, the decomposition is restored and the output is a signal with slight distortion.
Wavelets have two characteristics - scaling factor and offset, the relationship between which roughly corresponds to the scaling operation. At small scales, compressed wavelets are used, they correspond to rapidly changing signals (high frequency). At large scales, wavelets are stretched, they correspond to slowly changing signals (low frequency). Unlike other transformation tools (Fourier transform, etc.) used in signal processing, wavelets allow you to analyze signals simultaneously in the frequency and time domains.
Wavelet transforms are divided into two groups: discrete wavelet transform (DWT) and continuous wavelet transform (CWT). Both conversions are continuous in time (analog) and can be used to represent analog signals. CWT allows all possible scaling and offset factors to be used, while DWT uses a subset of them (grid).
An important question is the choice of the basic wavelet (mother), of which there are quite a lot at present: wavelets of Morlet, Shannon, Haar, Daubechies, Symlet, Mexican hat, etc. [5].
Daubechies wavelet family is the most popular wavelet family used for texture feature analysis, due to orthogonal and compact support abilities. The Daubechies wavelet uses overlapping windows, so the results reflect all changes between pixel intensities. Since Daubechies averages over more pixels, it is smoother than the Haar wavelet. The Daubechies D4 transform has four wavelet and scaling coefficients. The sum of the scaling function coefficients are also one, thus the calculation is averaging over four adjacent pixels.
The Symlets are nearly symmetrical, orthogonal and biorthogonal wavelets proposed by Daubechies as modifications to the db family. The properties of the two wavelet families are similar.
The choice of the wavelet type depends on the tasks. For noise reduction, the wavelet must have the properties of orthogonality and signal recovery. Symlet wavelets (sym) and Daubechies wavelets (db) are suitable for these purposes. By default, sym5 [98] is used for noise reduction in MatLab [6-8].
3. Implementation methodology
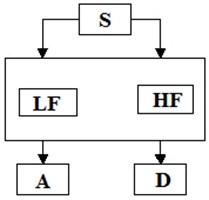
For most signals, their low-frequency component is the most important part because it can be used to identify the signal. The high-frequency component, in turn, carries the outline of the signal. However, if you remove a lot of low frequency components, the signal will become unrecognizable. In wavelet analysis, approximations are investigated on large scales, low-frequency components and details - on small ones. In Fig. 1 shows signal decomposition using wavelet analysis, where LF is a low-pass filter, HF is a high-pass filter, A is an approximation, D is a detail [9, 10].
Fig. 1Signal decomposition using wavelet analysis
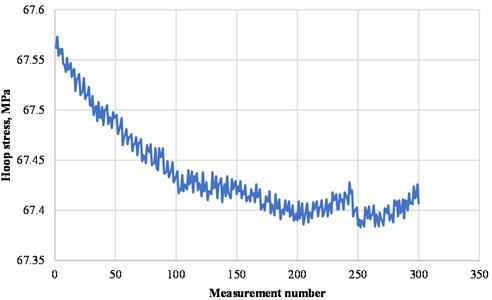
When applying the wavelet transform to gas pressure trends in gas pipelines, an increase in the accuracy of pressure control should be expected. Small changes in differential pressure may not be noticeable against the background of signal noise. Such changes can be detected after processing the original signal using a wavelet transform. Let’s analyze the time trend of the cycle voltages. The wavelet transform is performed in the MatLab interactive algorithm development environment.
Fig. 2Time trend of pipeline hoop stresses
The main script that went into the program looks like this, where wname is the wavelet that is being processed at this stage; level - level of decomposition:
x1 = xlsread('D:\wave\before.xlsx');
sig = x1;
wname = 'sym5';
level = 5;
[C,L] = wavedec(sig,level,wname);
sigd = wden(sig,'rigrsure','s','sln',level,wname);
figure;
subplot(2,1,1);
plot(sig); title('noisy signal'); hold on; plot(sigd); title('denoisy'); hold off
For comparison, the trend processing was performed by two types of wavelets suitable for noise reduction - Symlet and Daubechies wavelets.
The Fig. 2 shows the initial trend of the hoop stresses, Figs. 3 and 4 show the trends after applying the wavelet transform by the Symlet and Daubechies wavelets, respectively.
A similar processing was carried out for the time trends of the pressure at the inlet of the compressor station.
Fig. 3Hoop stress trend after processing with the Symlet wavelet
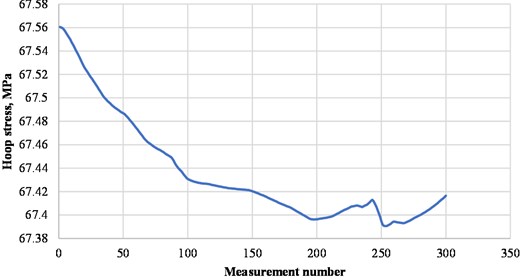
Fig. 4Hoop stress trend after processing with the Daubechie wavelet
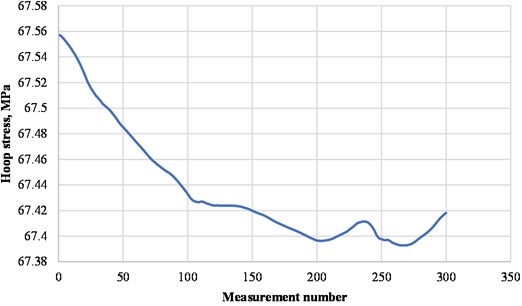
Fig. 5Initial pressure trend at the compressor station inlet before treatment
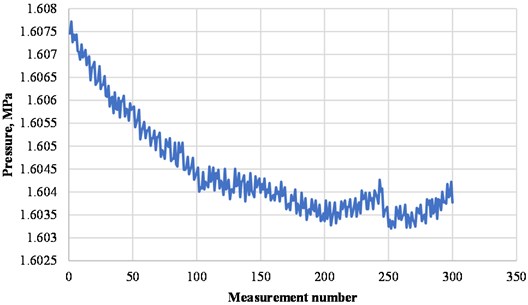
As can be seen from the figures, when processing the data using the Symlet wavelet, the graph peaks are more pronounced than when processing the Daubechies wavelet. Also, when the Daubechies wavelet is applied, some changes in the graph are smoothed out and become almost invisible. Thus, in the case of processing pressure trends and hoop stresses, it is most expedient to use the Symlet wavelet.
As a criterion for the deviation of the purified signal from the initial value at each point, the following value was taken:
Fig. 6Time trend of pressure at the inlet of the compressor station after processing by the Symlet wavelet
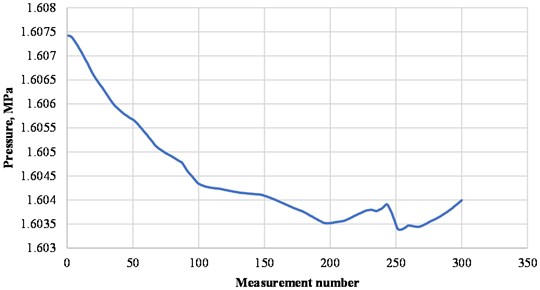
Fig. 7Time trend of pressure at the inlet of the compressor station after processing by the Daubechie wavelet
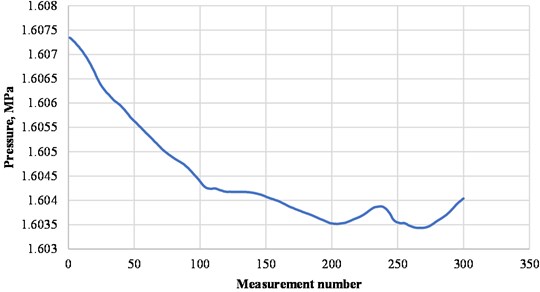
The deviation at each point of the purified hoop stress trend from the initial one when using the Symlet wavelet was from 0,00228 % to 0,01397 %, when using the Daubechies wavelet - from 0,00714 % to 0,01671 %.
Similar deviations were found for the pressure trend: when using the Symlet wavelet – from 0,00228 % to 0,01397 %, when using the Daubechies wavelet – from 0,00714 % to 0,01671 %.
Thus, when you remove an insignificant part of the original signal, the graphs of the change in values become more visual. It becomes possible to see the changes that were implicit before the noise was cleared. In particular, the application of the wavelet transform to the time trends of pressure makes it possible to localize small pressure waves with high accuracy against the background of a high noise level of the signal, which can facilitate the determination of leaks through small-diameter holes.
4. Conclusions
In this paper, a signal denoising method based on the wavelet tranformation has been proposed in order to improve the accuracy of measuring the pressure in the gas pipeline and noise suppression of the pressure sensor signal.
When comparing the use of two types of wavelets – Simlet and Daubechies, it was found that the Simlet wavelet transforms the signal more clearly, with a smaller deviation of the cleaned signal from the original - the deviation when using the Simlet wavelet was from 0,00228 % to 0,01397 %, when using the wavelet Daubechies – from 0,00714 % to 0,01671 %.
The method has been used to filter noisy signals, and it has been applied to natural gas pipeline signal from pressure sensors. The experiment has been demonstrated that this method could effectively filter out noise, and retain the original signal characteristics of pipeline.
References
-
Moskovsky, S. B., Sergeev A. N., and Lalina N. A., “Cleaning the signal from noise using the wavelet transform,” Technical Sciences: Electronic Scientific Journal, Vol. 2, 2015.
-
Y. Y. Betev, “Application of signal decomposition based on wavelets for pressure wave localization problems,” Bulletin of the Tomsk Polytechnic University, Vol. 317, No. 5, pp. 145–148, 2010.
-
K. Dragomiretskiy and D. Zosso, “Variational mode decomposition,” IEEE Transactions on Signal Processing, Vol. 62, No. 3, pp. 531–544, Feb. 2014, https://doi.org/10.1109/tsp.2013.2288675
-
R. Singh, R. E. Vasquez, and R. Singh, “Comparison of Daubechies, Coiflet, and Symlet for edge detection,” AeroSense ’97, Vol. 3074, pp. 151–159, Jul. 1997, https://doi.org/10.1117/12.280616
-
H. Gao, L. Ma, H. Dong, J. Lu, and G. Li, “An improved two-dimensional variational mode decomposition algorithm and its application in oil pipeline image,” Systems Science and Control Engineering, Vol. 8, No. 1, pp. 297–307, Jan. 2020, https://doi.org/10.1080/21642583.2020.1756523
-
N. K. Smolentsev, Wavelet Analysis in MATLAB. DMK Press, 2010.
-
Yansun Xu, J. B. Weaver, D. M. Healy, and Jian Lu, “Wavelet transform domain filters: a spatially selective noise filtration technique,” IEEE Transactions on Image Processing, Vol. 3, No. 6, pp. 747–758, 1994, https://doi.org/10.1109/83.336245
-
S. G. Chang, Bin Yu, and M. Vetterli, “Adaptive wavelet thresholding for image denoising and compression,” IEEE Transactions on Image Processing, Vol. 9, No. 9, pp. 1532–1546, 2000, https://doi.org/10.1109/83.862633
-
A. G. Lazareva, “Wavelet transform mathematics,” Young Scientist, Vol. 3, pp. 30–34, 2009.
-
N. M. Astafieva, “Wavelet analysis: Foundations of the theory and examples of application,” Uspekhi Fizicheskikh Nauk, Vol. 166, No. 11, p. 1145, 1996.

