Optimal 5R parallel leg design for quadruped robot gait cycle

1. Introduction

Robots are designed based on the tasks they are supposed to carry out. They are expected to be robust, dextrous [1] and reliable. Based on tasks, the designers have two options for robot design; to have a closed chain or an open chain mechanism.

In case of open chain mechanism, the stiffness is low [2], precision – positioning is slightly compromised and moreover huge amount of actuator torque is wasted which decreases the dynamic performance, but, their workspace reach is high. To overcome disadvantages of serial manipulators, parallel configuration was developed [3-7]. Few researchers have worked on parallel mechanism [8] to increase their workspace [9-12].

Parallel manipulators have higher payload carrying capacity, accuracy, and stiffness. Parallel mechanisms have low reach or small workspace and above that there are few occurrences of singularities. Instantaneous change in degree of freedom occurs whenever a singular configuration is attained which could be catastrophic is some cases. Thus, the study of singular configuration is essential [13]. Researchers have done extensive studies on singularity analysis [6, 14-17].

There are two types of singularities which are commonly observed in parallel mechanisms; Type 1 and Type 2 [4]. In Type 1, the end-effector will lose one or several degrees of freedom. In Type 2, at this configuration the actuator will not resist a force applied to end-effector. Conventional solutions were presented in [11, 18-21]. However, the solutions are not appreciable in all scenarios.

The requirement is precise motion so in order to achieve it, all singularities must be avoided, mechanism should be synthesised [22] and trajectory planning should be done [23]. There are many sets of solutions possible for inverse kinematic problem of parallel mechanism [8, 14]. Two Jacobian matrices are used to relate input – output velocities.

The paper presents optimal link lengths and orientation for parallel leg mechanism. In Section 2 and 3, the problem formulation is presented. In Section 4, results obtained by simulations are discussed. Finally, the conclusions are presented.

2. Model of the 5R parallel leg

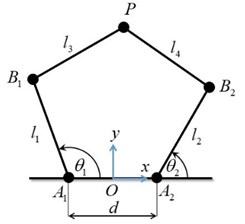
The schematic diagram of the 5R parallel leg considered in this paper is shown in Fig. 2. Links 1 and 2 of lengths $l_1$ and $l_2$ are the proximal links, and links 3 and 4 of lengths $l_3$ and $l_4$ are the distal links. From the reference coordinate frame with origin at $O$, revolute joints of the actuated links 1 and 2 are at a distance of $d/2$ on either side along $x$-axis. Fig. 1 shows the trajectory of the point $P$.

Fig. 1Path trajectory

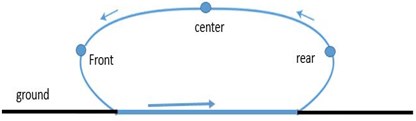
Fig. 2Schematics of the 5R parallel leg structure

2.2. Inverse position kinematics

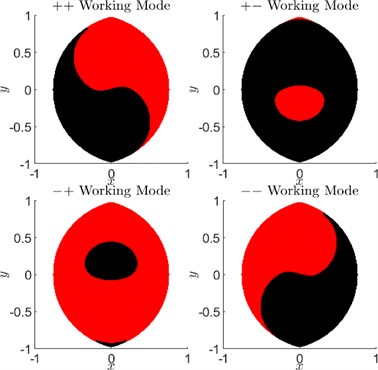
Inverse position kinematics consists of determining the joint angles ${\theta }_1$ and ${\theta }_2$ given the end-effector position $\left(xy\right)$. For every end-effector position within the reachable workspace of the 5R parallel robot manipulator, there are, in general, four solutions. These four solutions are categorized based on whether links 1 and 3 or links 2 and 4 make included angles less than $\pi$ or greater than $\pi$ measured from proximal links 1 or 2. For instance, in Fig. 2, the odd numbered links 1 and 3 make an angle less than $\pi$ (considered '-') and the even numbered links 2 and 4 make an angle greater than $\pi$ (considered '+'). This can be easily determined by checking the signs of $A_1{B}_1\times A_{1}P$ and $A_2{B}_2\times A_{2}P$. Using this convention, the four solutions, which are also called working modes, are described as ++, + -, -+, and --. Again, for each of these working modes there exists two assembly modes which divide the workspace of that particular working mode. Movement in the workspace from one assembly mode to another requires disassembly of joint at the end-effector.

For $l_1=l_2=l_3=l_4=d$, the workspace is maximum without holes in it as shown in Fig. 3.

Fig. 3Working modes and assembly modes

3. Torque requirement

The relationship between joint torques at $A_1$ and $A_2$, and the force applied at the end-effector on external surface is given by:

where $\tau ={\left[{\tau }_1{\tau }_2\right]}^T$ and $F={\left[F_x{F}_y\right]}^T$ and the Jacobian matrix:

It is clear that both $A$ and $B$ should be full rank to uniquely solve for joint torques, given the force required at the end-effector. We assume that the manipulator does not pass through singularities during normal usage and hence full rank Jacobian is ensured.

The following assumptions are considered as requirements or objectives of the leg structure:

1) End-effector path of the stance leg is a straight line parallel to the body of the quadruped robot during forward motion of the robot while maintaining a constant height.

2) End-effector path of the swing leg is a curve designed to lift the end-effector off the ground and take it to the next foot-hold on the ground. In addition to just lifting off the ground, the path should also circumvent any obstacles present.

3) End-effector can be placed on the ground at any desired foot hold within the limitations of the workspace of the parallel leg structure.

These objectives have to be met with least amount of torque from the actuators.

For constant height motion in trot gait, the vertical ground reaction force is equal to half of the total weight. For a friction coefficient of $\mu$, the maximum horizontal force will be $\mu$ times the vertical force. Let the Jacobian matrix be written as:

where $a_{ij}$ are elements of the Jacobian matrix dependent on $x$, $y$, ${\theta }_1$, and ${\theta }_2$.

In the configuration shown in Fig. 2, with the coordinate frame’s $y$-axis pointing upwards, the force that the leg mechanism has to generate is negative ($F_y<0$). The horizontal force $F_x$ can be either positive or negative depending upon acceleration or decceleration of the robot body. Then Eq. (5) can be written as:

Since we are interested in the magnitude of torques:

We can see from Eqs. (10) and (11) that the vertical force $⌊F_y⌋$ is just a scaling factor for the joint actuator torques. The coefficients of $⌊F_y⌋$ in Eqs. (10) and (11) depend on kinematics alone, i.e., end-effector position trajectory.

Now the problem of joint torque minimization can be stated as follows: For the given height of the robot body (or location where joint actuator is present) from the ground level and the given step length, find the dimensions $l_1$, $l_2$, $l_3$, $l_4$, and $d$ such that the peak absolute values of joint actuator torques ${\tau }_1$ and ${\tau }_2$ are minimum.

4. Results

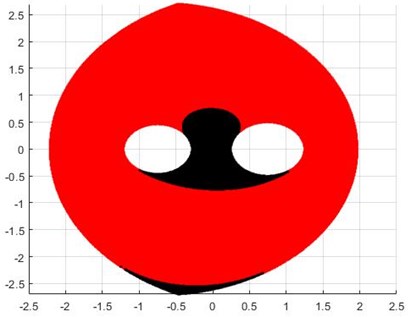
The minimization problem is solved used genetic algorithm. We are optimizing the peak torques of two actuators of this two degree of freedom mechanism to get optimal link lengths. Fig. 4 shows the workspace of the parallel mechanism. The link lengths obtained are $l_1=$ 1.1257 m, $l_2=$ 1.2306 m, $l_3=$ 1.5887 m, $l_4=$ 1.7296 m and $d=$1.4937 m. The torque for the path is obtained as 0.264 Nm.

In this paper, we assumed the path is symmetric as shown in Fig. 1 and solving the -+ mode we get the workspace depicted in Fig. 4. There are two types of singularities that can occur while working with parallel mechanism, they are Type I and Type II. In Type I singularity the mechanism loses one degree of freedom, i.e., if one link will follow the motion specified for other link and give some undesirable result. The other type of singularity is Type II, in this case the mechanism will attain some configuration and the actuator will not resist a force applied to end-effector, the actuator should have infinite stiffness which is not possible in practice and thus the end-effector cannot resist any force applied.

The path obtained does not have any Type I singularities.

Fig. 4Workspace obtained after optimization

5. Conclusions

In this paper we found out the optimized link length for the parallel manipulator. The criteria were set as to get maximum horizontal straight path but at minimum expense of torque. Here we have assumed that the path is symmetric (Fig. 1). In next case we would like to formulate asymmetric case and find out the optimized path. In the present study we have considered only the “–+” mode which seemed more promising, in future we want to analyse the remaining modes and study which one would yield the best result that can be incorporated for quadruped gait.