Effect of vibration on the rheological properties of glycerin during its purification

1. Introduction

Recently, suspensions and emulsions have received a great deal of attention [1]. Several research works have been focused on the rheology of suspensions and emulsions because the rheological properties of such inhomogeneous systems determine their technological characteristics [2].

Various scientific researches have been devoted to the study of the rheological behaviors of Glycerol under some stress and temperature [3]. The Glycerol has also been named “glycerin” in some documents like [4]. However, glycerin is the commercial name of Glycerol, which is not pure, and contain mostly 95 % of Glycerol. Glycerol is the triol compound used for different purposes in pure or mixed forms. High-purity glycerin (at least 99 %) is obtained by the alcoholization of vegetable fats, using vacuum distillation. Afterwards, the material would be separated the separation from the impurities by gravitational deposition.

The raw glycerin is a non-Newtonian fluid because it is a suspension that consists of a large number of micro dispersed inclusions. A non-Newtonian fluid is called a fluid that has a linear relationship between shear stress and the strain rate [5]. The inclusions of raw glycerin similar to those of other non-Newtonian materials dramatically influence the structure of the material, while rheological characteristics change [6]. Also, the relaxation time of such liquids is in the range of 1 ps to 1 ns [7]. The range of relaxation time of Glycerol, as a non-Newtonian liquid, is closely related to the motion of macroscopic objects. These liquids could be well described by the classical Navier-Stokes methods [8].

Ayala et al. [9] studied the effects of temperature and glycerol concentrations on the changes in rheological properties of potato starch solutions. It has been reported in [9] that the Herschel-Bulkley model was the best one for studying the behavior of mixtures with different concentrations of Glycerol at different temperatures. The characteristics of pseudoplastic solutions could be concerned in the Herschel-Bulkley model. In addition, the effects of glycerol concentration on the change in rheological parameters of the mixture have been modeled by a second-degree polynomial. However, it has been presented that a linear relation between the concentration and the temperature of the mixture should be considered to model the shear stress behavior, which depends on the glycerol concentration.

In [10], a new refinement of the value of the shear stress of Glycerol has been introduced. This paper also presented a new correction procedure to obtain shear stress relaxation curves based on experimental data. Chen et al. [11] reported a numerical method to determine the rheological characteristics of viscoelastic structures with complex geometry. They proposed a finite element method (FEM) for problems in this class. In [12], it has been tried to decrease the errors in the numerical calculations due to the approximated inversion method approaches. In addition, the Norton rule was applied to simulate the specific behaviors of viscoelastic materials and their stress-strain-time state.

Although the influence of structural and mechanical properties of the material and the conditions of their deformation under vibration conditions is significant, it is also worth paying attention to the previous technology of material processing. Thus, [17] dealt with the phenomenon of structural relaxation of the material after its preliminary thermomechanical treatment. Understanding structural relaxation and its influence on the properties of the material is extremely important for assessing the manufacturability and efficiency of dispersed materials’ processes depending on the conditions of their preparation and its “thermal history”. However, the concept of this phenomenon is vital for the development of effective technical equipment.

The stress of the material and its shear rate are important indicators in rheology [13, 14]. These indicators characterize the viscosity and elasticity of the dispersed material (suspensions and emulsions) during the deformation process. Suspensions and emulsions in rheological models should be considered as two-phase systems [15], while their viscosity is determined. Consideration of the parameters of the machining of the material, such as pressure and force, is crucial to model the rheological characteristics accurately. Otherwise, the assessment of materials’ rheological characteristics would be significantly complicated and inaccurate.

The deployment of vibration-based technologies is steadily growing to process various materials [16, 17]. The effectiveness of vibration-based processes depends on the construction of the equipment, modes of material processing, and rheological properties [18]. Although the impacts of vibration in the separation of heterogeneous dispersed systems significantly intensify this process, there is a research gap about studying the vibration influence on the rheological characteristics of the material.

A few types of research like have been performed to distinguish the vibration influence on the rheological characteristics of Glycerol. In [16], as one of the previous research works of this paper’s authors, the experimental results of a new vibrating center machine for glycerin purification have been studies. The principle of operation of the introduced machine in [16] is to combine the centrifugation and vibration separation processes. The glycerin is separated into a liquid fraction and sediment because of applying the centrifugal forces. Afterwards, the of glycerin would be separated from the precipitate under the influence of vibration.

The mechanic-rheological methods [19, 20] are widely used to select the optimum technological parameters of material processing based on vibration-based processes. This is mainly because of the simultaneous consideration of the interaction of the machine’s mechanical characteristics and the material’s rheological characteristics in the mechanic-rheological methods. In this paper, the new mechanic-rheological studies are proposed to identify the effective operating modes of machine introduced in [16], which is useful for glycerin purification based on combinatorial centrifugation and vibration separation processes. Developing mathematical evaluations based on the experimental results is one of the most important contributions of this paper. Test results illustrate the advantages of the proposed method.

The main contribution of this work is the development of a new method for estimating the rheological characteristics of raw glycerin. The compression device is used to perform this method. That allows establishing clearly the characteristic of unilateral deformation of glycerin at various technological modes of processing.

However, this method has some limitations. They mainly depend on the technological parameters of material processing. For example, the vibration frequency plays an important role in determining the rheology of a material. Starting from 150 rad·s^-1, there is a sharp increase in measurement error. That is why at the high frequency it is necessary to use additional dampers for the compression device.

The organization of the rest parts of the paper is as follows. In Section 2, the materials and the proposed methodology are given. The test results are presented in Section 3. Finally, Section 4 reports the conclusion.

2. Materials and methods of research

In this study, a new approach is proposed to determine the effective operating modes of machine introduced in [16], which is useful for glycerin purification based on combinatorial centrifugation and vibration separation processes. The mathematical mechanical-rheological evaluations are developed based on the experimental results.

2.1. Overview of the experimental set-up

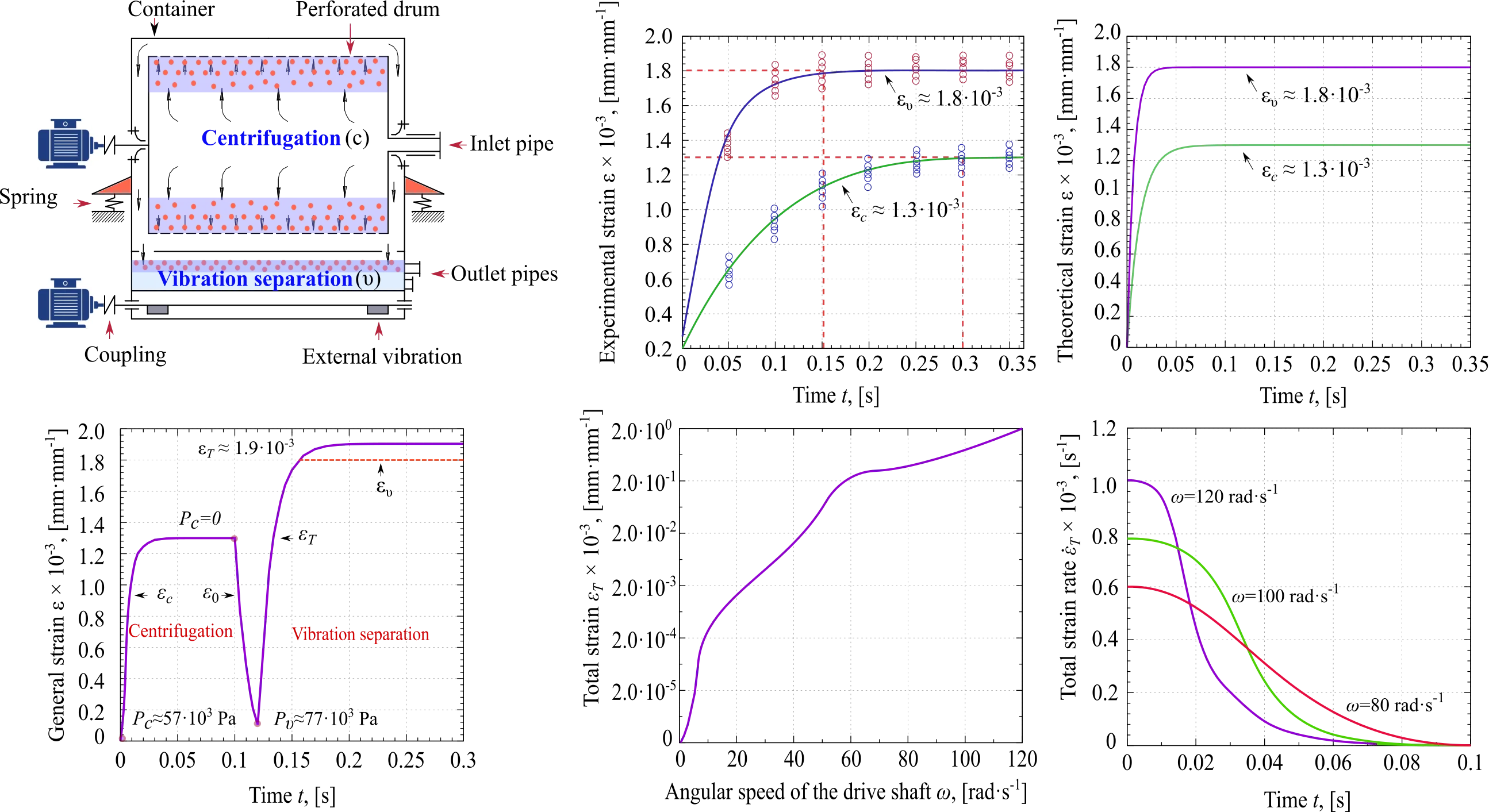
The experimental set-up and technological scheme of the developed vibrocentric machine, which has been introduced in [16], are shown in Fig. 1(a) and Fig. 1(b), respectively. This vibrocentric machine is useful for glycerin purification, which is studied in this paper.

Fig. 1The understudy vibrocentric machine for raw glycerin purification: a) Experimental set-up and b) the technological scheme

a)

b)

The angular speeds of the vibrator’s driving shaft and the centrifuge rotor are similar and have been set to 120 rad·s^-1. Also, the oscillation amplitude of the container, the total mass of oscillating machine parts, and the productivity of this machine are 4-4.5 mm, 60 kg, and 90-94 L·h^-1, respectively. Moreover, the internal area of the perforated drum is 0.25 m², while the area of the container for the vibration separation is 0.05 m².

Conventionally, the technology of glycerin purification in this machine can be separated into two technological stages: preliminary and final purification. At the first stage, due to the action of centrifugal forces to provides the process of separation of glycerin into liquid fraction and ash. Then the separated material is moved to the vibrating container. There, due to the influence of vibration, the final purification of glycerin takes place. The main purpose of the last technological operation is to extract the glycerin from the ash that formed after the first technological operation. Schematically flowchart of glycerin purification technology by vibrocentric machine is shown in Fig. 2(a).

In this study, the third-grade raw glycerin of the third grade is used to perform the experimental material tests, which its characteristics could be presented as Table 1.

The experimental-theoretical method was used to search for rheological coefficients for glycerin at different stages of its processing. Firstly, a compression device is used to find the magnitude and time of deformation of glycerin at different parameters of technological influence. Afterwards, the stress and viscosity of glycerin are calculated from the Kelvin-Voigt equation. Schematically flowchart of finding rheological coefficients by the experimental-theoretical method shown in Fig. 2(b).

Table 1Specifications of tested glycerin

No.	Specification	Value
1	Viscosity at 37 °C	382·106 Pa·s-1
2	Bulk modulus at 23 °C	4.52 109 N m-2
3	Density	1.26 kg·m-3
4	Organic residue at 20 °C	4.3 %
5	Mass fraction at 20 °C	76.8 %

Fig. 2a) Flowchart of glycerin purification by vibrocentric machine: b) flowchart of finding rheological coefficients. Accordingly to the figure, the following symbols occur: Tg is Glycerin temperature; ω is angular speed of rotation of the driving shaft; A is oscillation amplitude of the vibrocentric machines; Pp is pumping performance; Pc is centrifugal pressure; Pυ vibrational pressure; Xp.gl., Xash and Xo.r.is a mass fraction of pure glycerol, ash, and organic residue respectively; time tυ, tc of strain ευ, εc by vibration (υ) and centrifugation (c), respectively; ηυ viscosity of the material under vibration

2.2. Theoretical set-up

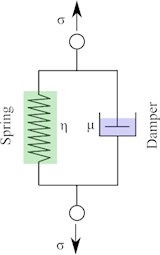
The crude glycerin, as the testing material of this study, is an elastic-viscous medium (non-Newtonian fluid). The Kelvin-Voigt rheological model is usually used to describe the unilateral deformation of such materials, as shown in Fig. 3 [21, 22]. This model consists of Hooke and Maxwell’s elements characterizing the elastic and viscous properties of the material, respectively. The mathematical expression of this model could be presented as Eq. (1):

1

$\sigma =E\epsilon +\eta \dot{\epsilon }.$

The feasible solutions of Eq. (1) depend on material processing technology. It might have several processing stages. Each processing stage leads to some deformation in the material as a result of mechanical influence on the material. In addition, some deformations would be done during the next technological stages of processing.

The stress of the material, including strain and shear rate terms, are very important because in the proposed case, complex vibration and centrifugal technology are used to purify glycerin in this research. The deployment of this technology combines combining two technological stages highlights the effectiveness of the Kelvin-Voigt rheological model. The glycerin’s modulus of elasticity is considered to be 4.35 GPa.

The centrifugation is the first technological stage of glycerin processing in the machine shown in Fig. 1(b). In this process, due to the centrifugal force, the internal structure of the material is slightly deformed. Afterwards, the vibration separation as the second technological stage starts. Finally, the material already would have some residual deformations.

Fig. 3Schematic representation of the Kelvin-Voigt rheological model

Two different solutions of Eq. (1) could be determined based on the above-stages. In the centrifugation as the first stage process, the material has no previous deformation. On the contrary, in the vibration as the second stage process, the material has experienced a prior deformation. Hence, the solution of (1) in the centrifugation process as the first stage, while $\epsilon \left(0\right)=$0 is the initial condition, could be given in Eq. (2):

2

$\epsilon =\frac{\sigma }{E}\left(1-e^{\frac{-E\cdot t}{\eta }}\right).$

In the second stage at the initial condition ($\epsilon \left(0\right)={\epsilon }_0$), which is the final condition of the centrifugation process, the strain of the material would be as:

3

$\epsilon =\frac{\sigma }{E}+e^{\frac{-E\cdot t}{\eta }}\left({\epsilon }_0-\frac{\sigma }{E}\right).$

The controlling of vibration settings is an effective means of controlling the dynamic state of the dispersion process. The vibration causes an intense mutual movement of the particles, which sharply increases the speed of each particle relative to their centers of mass. In this case, the properties of the dispersed systems depend on the ratio of the mass of the particles and their acceleration. The magnitude of the coupling force would be much smaller than the value of the vibration impulse. Therefore, it is concluded that the technological parameters of the vibration source have a significant impact on the rheological properties of the material.

Based on the above explanations, it is necessary to modify Eq. (1) to reflect changes in the rheological characteristics of the material accurately. The modified mathematical modeling should represent both centrifugal and vibrational effects on the material.

In this paper, the general mathematical model of deformation of a viscoelastic material, which is developed for the new glycerin purification method, could be expressed in Eq. (4):

4

${\sigma }_T+kA\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega \tau \right)=E{\epsilon }_T+\eta {\dot{\epsilon }}_T.$

The general solution of Eq. (4) at $\epsilon \left(0\right)=0$ and $\epsilon \left(0\right)={\epsilon }_0$ would be as Eq. (5) and Eq. (6), respectively:

5

$\begin{array}{l}{\epsilon }_T=\frac{e^{\frac{-tE}{{\eta }_v}}{e}^{\frac{-tE}{{\eta }_v}-1}\left({\sigma }_T{E}^2+{\sigma }_T{\eta }_v^2{\omega }^2+Ak{E}^2\mathrm{c}\mathrm{o}\mathrm{s}\left(\tau \omega \right)+Ak{\eta }_v\omega E\mathrm{s}\mathrm{i}\mathrm{n}\left(\tau \omega \right)\right)}{\left({\eta }_v^2{\omega }^2+E^2\right)}\\ -\frac{e^{\frac{-tE}{{\eta }_v}}\left({\sigma }_T{\eta }_v^2{\omega }^2+{\sigma }_T{E}^2+Ak{E}^2\right)}{\left(E{\eta }_v^2{\omega }^2+E^3\right)},\end{array}$

6

$\begin{array}{l}{\epsilon }_T=\frac{e^{\frac{-tE}{{\eta }_v}}\left({\epsilon }_0-\left(E^{-1}{\sigma }_T{\eta }_v^2{\omega }^2+{\sigma }_{T}E+AkE\right)\right)}{\left({\eta }^2{\omega }^2+E^2)\right)}\\ +\frac{e^{\frac{-tE}{{\eta }_v}}{e}^{\frac{-tE}{{\eta }_v}-1}\left({\sigma }_T{E}^2+{\sigma }_T{\eta }_v^2{\omega }^2+Ak{E}^2\mathrm{c}\mathrm{o}\mathrm{s}\left(\tau \omega \right)+Ak{\eta }_v\omega E\mathrm{s}\mathrm{i}\mathrm{n}\left(\tau \omega \right)\right)}{\left({\eta }_v^2{\omega }^2+E^2\right)}.\end{array}$

2.3. Compression device

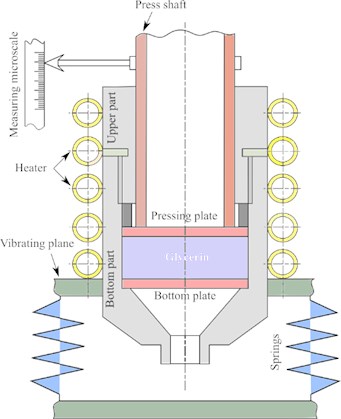
In this paper, the compression device was used to determine the value of deformation, which characterizes the properties of the material at different technological stages. This device has been developed at the National University of Food Technology, Ukraine, as shown in Fig. 4.

As can be seen in Fig. 4, the compression device consists of a cylindrical body, which its bottom part is fixed on the vibrating plane. A 1 dm³ dose of glycerin is loaded inside the cylindrical body, between the pressing and bottom plates. Moreover, the compression chamber has been shaped like a cylinder: 10 cm diameter and 13 cm height, while a pressing shaft provides the compression of glycerin.

A measuring microscale has been used to identify the value of the material’s deformation during the compression. The temperature of the glycerin has been considered to be 60 °C based on the data of [16], which is controlled using a heater.

The developed construction of the selected compression device is very successful because it could be used to search for materials’ rheological coefficients at different processing.

Fig. 4The compression device for determining the rheological coefficients

In the experimental tests, the vibration frequency sweep from 10 rad·s^-1 to 120 rad·s^-1 has been applied. In addition, different material’s compression forces have been examined. For the centrifugation process, the compression pressure ($P_c$) is assumed to be about 57·10³ Pa.

The vibration pressure ($P_{\upsilon }$) is utilized to estimate the force influence on the material during vibration separation. It should be noted that the vibration pressure is dramatically dependent on the value of the angular speed ($\omega$) of the vibrating machine. The required vibration pressure ($P_{\upsilon }$) is generated using the vibration plane of the compression device. Therefore, for further research, it is essential to determine the magnitude of the vibration pressure, particularly based on the designed and implemented experimental set-up.

Firstly, the magnitude of the oscillatory force ($F_{\upsilon }$) for vibration machine should be determined multiplying the vibration acceleration ($a_z$) and the total mass of the oscillating part of the vibration machine. Then, the vibration force’ value is divided by the size of the area of the vibration separator, and the vibration pressure ($P_{\upsilon }$) on the glycerin would be determined.

In the proposed approach to determine the rheological coefficients of raw glycerin purification, the duration ($t$) and the magnitude of deformation ($\epsilon$) of the material are determined using the compression device. Then, the deformation’s magnitude against the deformation time would be evaluated based on the measured experimental results. Furthermore, different rheological properties of various conditional materials are studies in this paper.

As discussed, it is possible to identify the value of modulus of elasticity ($E$) as a function of $\sigma ·E^{-1}$. Afterwards, the value of stress of the material ($\sigma$) could be calculated using the value of $E$, according to Eq. (2) and Eq. (3).

3. Results and discussion

In Fig. 5, the changes in the amplitude of oscillation Fig. 5(a) and the vibration acceleration Fig. 5(b) under different angular speeds of the driving shaft based on the experimental measurements have been shown. The method of conducting these experimental studies is presented in the paper [16].

Fig. 5Experimental results of a) oscillation amplitude and b) vibration acceleration depending on the angular speed of the driving shaft

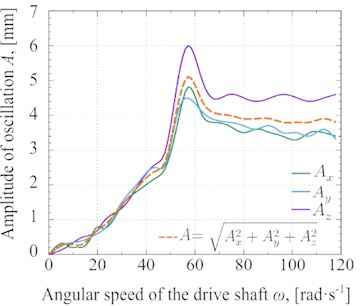
a)

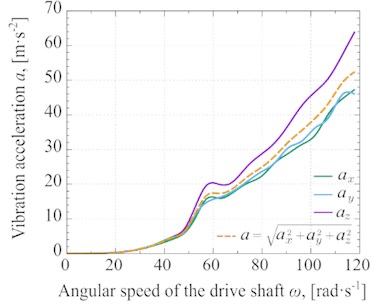
b)

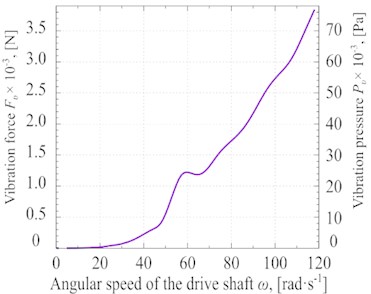
In addition, the magnitude of the oscillatory force ($F_{\upsilon }$) for vibration machine is shown in Fig. 6(b). The oscillatory force ($F_{\upsilon }$) is determined according to multiplying the vibration acceleration (as shown in Fig. 5(b)) by the total mass of the oscillating part, which is 60 kg. The value of the vibration force is divided by the area of applying the force (0.05 m²), and the vibration pressure on the glycerin ($P_{\upsilon }$) is calculated. The distributions of oscillatory for ($F_{\upsilon }$) and vibration pressure ($P_{\upsilon }$) as functions of angular speed ($\omega$) are shown in Fig. 6(b).

In Fig. 6(a), the trends of strain have been shown based on the Kelvin-Voigt rheological model. As discussed in the proposed methodology, the duration ($t$) and the magnitude of deformation ($\epsilon$) of the material using the compression device are distinguished. In this study, three conditional materials have been tested. As revealed by Fig. 6(a), the magnitude of deformation increases up to reach the steady-state value, which is equal to $\sigma ·E^{-1}$. It is evident that different conditional materials result in different durations of deformation.

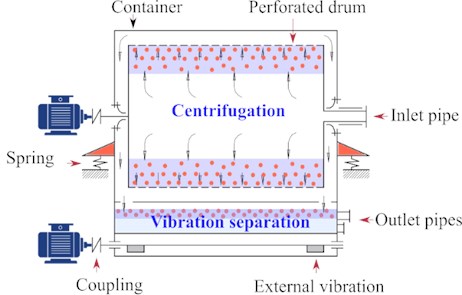
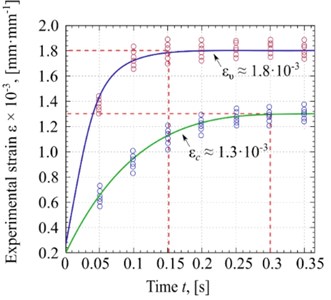
The dependencies of strain ($\epsilon$) are determined using the compression device under the centrifugation-based process and simultaneous centrifugation and vibration processes. The results of the obtained experimental data showing the strain ($\epsilon$) under different types of processes are presented in Fig. 6(c). As can be seen, the circle points have been shown for experimental data, and the appropriate curves have been fitted based on the measured experimental data.

Test results infer that the vibration greatly accelerates the value strain of the glycerin. The comparison of test results shows that the maximum value of strain would be ${\epsilon }_{\upsilon }\approx$ 1.8·10^-3 mm·mm^-1 at $t=$ 0.15 s under the vibration-based process, while the maximum value of strain is ${\epsilon }_c\approx$ 1.3·10^-3 mm·mm^-1 at the time $t=$ 0.30 s under centrifugation-based process. The faster and higher strain is achievable by applying the vibration-based process.

It has been assumed that the value $e^{\left(\eta t\right){\mu }^{-1}}$ could be neglected to calculate the rheological coefficients. The typical calculations of rheological coefficients for raw glycerin purification at the specific parameters ($P_c\approx$ 57·10³ Pa and $P_{\upsilon }\approx$ 77·10³ Pa) are presented to clarify how the proposed method could be implemented.

The ${\sigma }_c$_, as one of the rheological coefficients under the process without vibration, could be determined using Eq. (7):

Fig. 6Deformation kinetic curves: a) Strain for conditional curves of different materials at σ= constant and ε0= 0, b) the distribution of Fυ and Pυ versus the ω, c) experimental strain trend of glycerin deformation without the vibration process at Pc≈ 57·103 Pa and with the vibration process at Pυ ≈ 77·103 Pa, d) theoretical strain diagram of glycerin

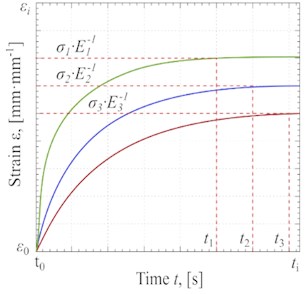
a)

b)

c)

d)

Also, the ${\sigma }_{\upsilon }$_, as one of the rheological coefficients under the vibration-based process, could be calculated using Eq. (8):

Afterwards, the values of $\eta$ as another rheological coefficient under both processes could be evaluated using Eq. (9) and Eq. (10), which have been defined based on Eq. (2):

The methodology of [23] is used to solve the above equations. The values of ${\eta }_c$ and ${\eta }_v$ under the process without and with vibration are calculated, as shown in Eq. (11) and Eq. (12):

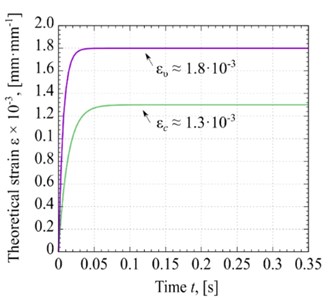
In Fig. 6(d), the theoretical curves of the strain against the compression duration under different types of processes. The first result that claims the attention is the difference between the ${\epsilon }_{\upsilon }$ and ${\epsilon }_c$. The strain of glycerin under the vibration-based process (${\epsilon }_{\upsilon }\approx$ 1.8·10^-3 mm·mm^-1) is greater than that of the process without vibration (${\epsilon }_c\approx$ 1.3·10^-3 mm·mm^-1). The comparison of test results illustrates that the theoretical strains curves are very similar to the experimental ones. But, the processing time in the theoretical curves is significantly different from the experimental values. The difference in the strain’s stabilization time of two types of process is about 0.05 s.

Moreover, the values of relaxation rate ($\lambda$) and retardation time ($\tau$) of the glycerin under two processing type are determined using the ($\eta ·E^{-1}$) and ($E·{\eta }^{-1}$), respectively.

The general characteristics of the rheological coefficients for glycerin under different non-vibration based and vibration-based process at $P_c\approx$57·10³ Pa and $P_{\upsilon }\approx$ 77·10³ Pa are shown in Table 2.

The residual strain of glycerin (${\epsilon }_0$) after the centrifugation could be determined according to Eq. (13). As shown, the strain of the glycerin is characterized when the deforming force suddenly finishes:

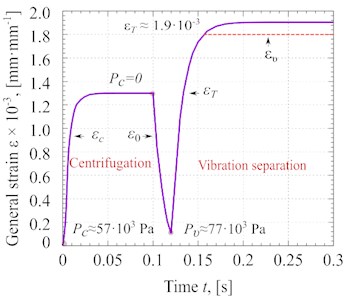
The speed of the material after centrifugation would be approximately 11 m·s^-1 based on the Bernoulli equation. The distance between the centrifuge rotor and the vibration separation section has been set to 0.2 m. While the $P_c$ is equal to 57·10³ Pa, the material falls into the zone of vibration separation at 0.018 s. Finally using the residual strain distribution over time, the value of ${\epsilon }_0$ is obtained to be 1.1·10^-4 mm·mm^-1. The general strain of glycerin processing in the developed vibrocentric machine is shown in Fig. 7(a).

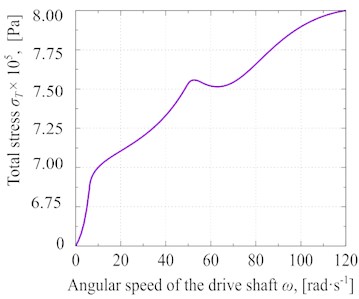
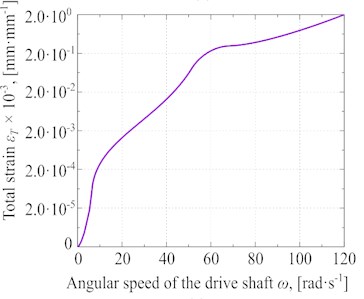
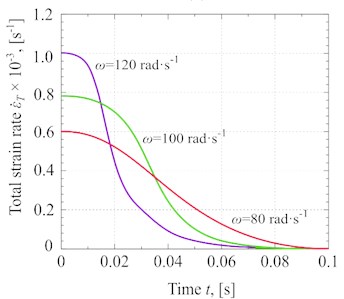
Fig. 7Different experimental results at Pc≈ 57·103 Pa and Pυ≈ 77·103 Pa: a) general strain distribution, b) total stress of the glycerin versus the angular speed, c) Total strain versus the angular speed, d) the total strain rate of glycerin under different angular speeds

a)

b)

c)

d)

As shown in Fig. 7(a), firstly due to the compression pressure ($P_c$), the strain of the material increases sharply to 1.2·10³ mm·mm^-1. Afterwards, the material is separated from the centrifuge rotor, and it would be prepared for vibration separation. In this step, the compression pressure stops suddenly. Although a sharp decrease in deformation in the material begins, due to the short distance between the material processing sections, the deformation of the material does not completely disappear. When the material enters to section for the vibration separation, it already has some strain (${\epsilon }_0\approx$ 1.1·10^-4 mm·mm^-1). In this section, vibration pressure ($P_{\upsilon }$) is applied to the material, which sharply increases the strain to ${\epsilon }_T\approx$ 1.9·10^-3 mm·mm^-1.

Then, the total rheological characteristics of glycerin, as a function of angular speed ($\omega$), are extracted using the rheological characteristics of Eq. (6). For instance, the equation for total stress could be given as Eq. (14):

Fig. 7(b) shows the ${\sigma }_T$ of the glycerin via changes in angular speed of the vibrocentric machine’s driving shaft. As revealed by results shown in Fig. 7(b), the total stress increases because of the increment of angular speed. The maximum total stress in the material at 120 rad·s^-1 is ${\sigma }_T\approx$ 8·10⁶ Pa. Also, a sharp increase in stress is observed, while the angular speed is around 50 rad·s^-1. This is mainly because of the vibrocentric machine’s resonance in this frequency range.

It is possible to determine the magnitude of total strain (${\epsilon }_T$) at the vibrational separation based on the obtained numerical data of ${\sigma }_T$, as shown in Fig. 7(c). The obtained curve of total strain has been divided into three segments. The middle part of this curve (from 15 rad·s^-1 to 60 rad·s^-1) has the sharpest increase in the value of total strain via the changes in the angular speed. However, it has been illustrated that the maximum amount of ${\epsilon }_T$ (2.0·10^-3 mm·mm^-1) at 120 rad·s^-1.

Finally, the strain rate of the glycerin could be evaluated based on the amplitude-frequency parameters of the vibration machine using Eq. (6).

Hence, the total strain rate of the glycerin could be given as Eq. (15):

Fig. 7(d) shows the total strain rate of glycerin against the angular speed of the vibrating machine’s driving shaft. The strain rate increases sharply due to an increase in the angular speed. It means that the increment of angular speed results directly affects the vibration pressure, which leads to accelerating the material’s deformation. For instance, the total strain rate of glycerin at $\omega \approx$ 120 rad·s^-1 is ${\dot{\epsilon }}_T\approx$1.0·10^-3 s^-1, while it would be 0.8·10^-3 s^-1 and 0.6·10^-3 s^-1 at $\omega \approx$ 100 rad·s^-1${\dot{\epsilon }}_T$ and $\omega \approx$ 80 rad·s^-1${\dot{\epsilon }}_T$, respectively.

The purification of glycerin is characterized by complex chemical, physicochemical, thermophysical and mechanical processes. The study of which makes it possible to organize effective and objective rheological control and management of technological purification cycles. Depending on the task, the studied rheological characteristics of glycerin can be used to determine the quality of the finished product and serve as initial data in the design of vibrocentric equipment.

4. Conclusions

In this paper, a new methodology has been proposed to evaluate the rheological characteristics of raw glycerin purification based on the experimental testing. A compression device has been used to determine the value of the unilateral deformation of this material, which allows simulating a condition of a material at various technological modes of processing. In this study, the changes of material properties under centrifugation and vibration separation processes in a vibrocentric machine have been investigated.

Mathematical modeling of glycerin’s deformation during its complex processing was developed. It was concluded based on the experimental and theoretical achievements that the influence of vibration by 15 % increases the amount of strain of the glycerin as opposed to the influence of centrifugal forces. Test results showed that the strain value and the material stress depended on the amplitude-frequency characteristics of the vibromachine. Test results inferred that the value of rheological coefficients increases with the increasing angular speed. Different rheological characteristics, e.g. the total stress, the total strain, and the total strain rate at different angular speeds of the vibrocentric machine’s driving shaft could be identified by applying the proposed methodology.

The development of a method to determine the rheological characteristics of bulk materials in the process of vibromixing is considered as one of the future works of this study.