Control of the air suspension system of semi-trailer trucks to enhance the road friendliness

2.1. Semi-trailer truck dynamic model

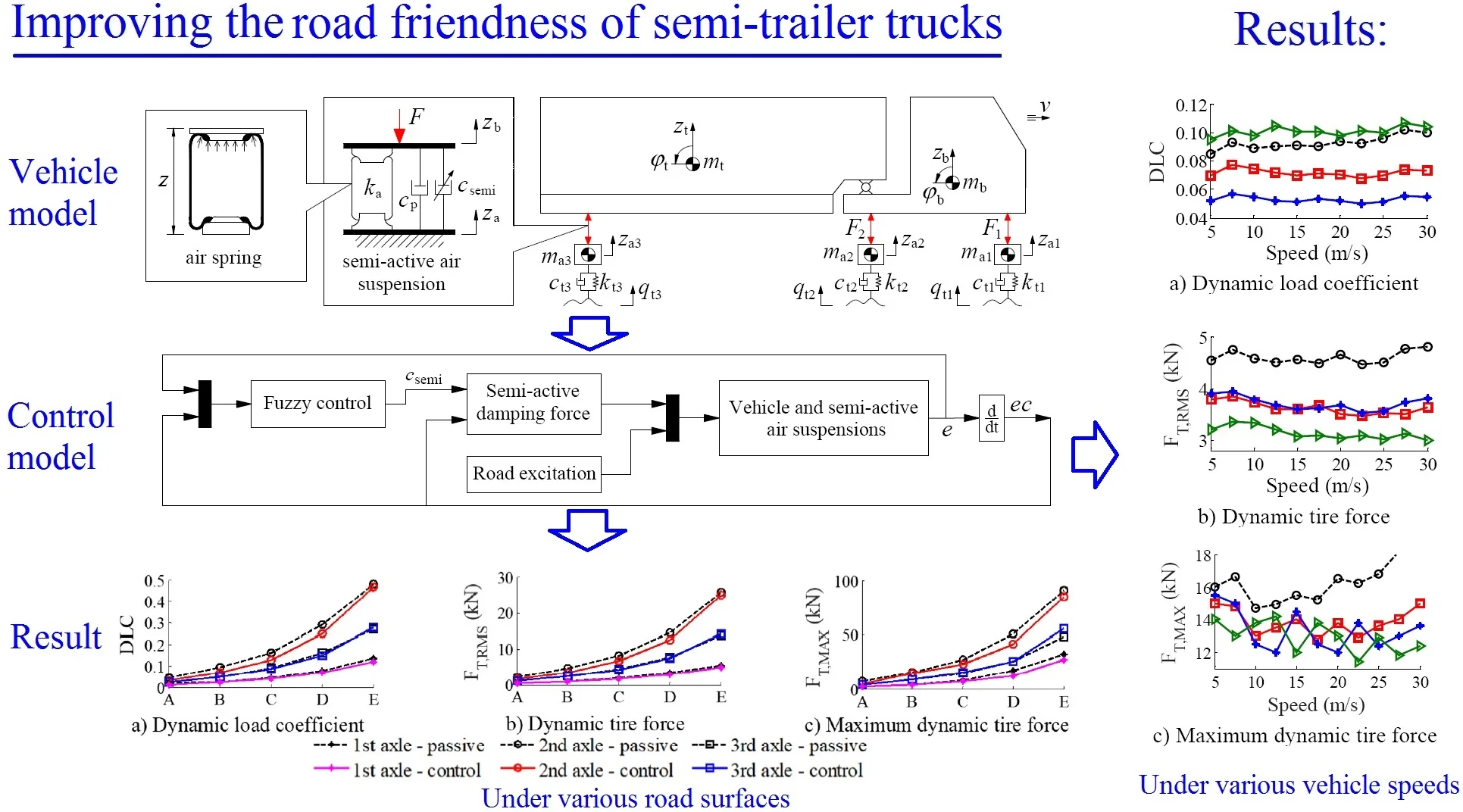
The structure of semi-trailer trucks includes the tractor driver, trailer, and three axles of the vehicle (steering, tractor driver, and trailer axles). A dynamic model of a semi-trailer truck with 7 degrees of freedom is then established as in Fig. 1, where, $m_b$ and $m_t$ are the sprung mass of the tractor driver and trailer. $m_{a\mathrm{1,2},3}$ are the unsprung mass of the steering axle, tractor driver axle, and trailer axle. $z_b$, $z_t$, and $z_{a\mathrm{1,2},3}$ are the vertical displacements of tractor driver, trailer, and vehicle axles. ${\phi }_b$ and ${\phi }_t$ are angular displacements of tractor driver and trailer. $q_{t\mathrm{1,2},3}$ is the excitation of the road surface roughness at tires.

Fig. 1A dynamic model of semi-trailer truck with semi-active air suspension system

Based on the vehicle dynamic model in Fig. 1 and by applying Newton’s second law, the motion equations of the vehicle can be represented in the matrix form as follows:

where $M$, $C$, and $K$ are the mass, damping, and stiffness matrices of vehicle, $Z$ is the displacement vector, and $F_q\left(t\right)$ is the force vector of the vibration excitation of the road surface.

2.2. Semi-active air suspension model

The air suspensions of semi-trailer trucks are used by the rolling lobe air springs and viscous dampers, and viscous dampers are controlled by semi-active fuzzy control, as modeled in the same Fig. 1.

The equation dynamic force of the air suspension system is written as follows:

where, $k_a$ is the stiffness coefficient of air spring. $c_p$ is the passive dumping coefficient. $c_{semi}$ is the semi-active damping coefficient. $z=z_a-z_b$ is the relative displacement of air suspension.

Based on the calculated result of the air spring in Ref. [3], the $k_a$ is determined by:

where, $A_0$ and $V_0$ are the initial effective area and volume, $\beta$ and $\alpha$ are the change of the effective area and volume with respect to $z$, $p_0$ and $p_a$ are the air pressure of the initial state and the standard atmospheric pressure, $n$ is a specific heat ratio.

4.1. Vibration excitations

To establish the random road surface, the white noise speed spectrum represented with a realization of a random process via its frequency spectrum density (FSD) is applied to describe the random road surface. Its equation can be expressed as follows [9]:

where, $\gamma$ is the spatial frequency of the road surface, $w\left(t\right)$ is the random signal of the white noise, $S\left(n_0\right)$ is the road roughness power spectrum density (PSD) chosen via ISO 8068 [14]. Based on ISO 8068, the PSD of road surface roughness of levels A, B, C, D, and E at $v=$ 20 m/s of the vehicle is chosen to simulate the excitation of the road surface roughness. The high roughness of the road surface with the simulation time of 50 s is shown in Fig. 3.

4.2. Evaluation criteria of road friendliness

Dynamic load coefficient (DLC) is frequently used to characterize the dynamic loading of the axles. It is defined by a ratio of the root-mean-square (RMS) of the dynamic load fluctuation over the static load [13]. The expression of the DLC is written by $DLC=F_{T,RMS}/F_s$. Herein, $F_{T,RMS}$ is the vertical RMS dynamic wheel load, $F_s$ is the average or nominal static vertical wheel load. The DLC value depends on several factors, such as road surface condition, type of suspension, vehicle velocity, load, mass, and stiffness distribution of the vehicle's structure. In general, it is in the range of 0.05 to 0.3 under normal operating conditions. It may reach to the zero when the wheels of a heavy truck are moving on a special smooth road or increase up to 0.4 when the contact between the wheels and the road surface axles is broken [9, 15]. In this study, the DLC is used to evaluate road friendliness.

5.1. Control of air suspensions on ISO level B

As clearly discussed in the previous sections, the paper aim is to reduce the DLC values of tire forces from heavy truck axles by controlling the semi-active air suspension system on the road surface roughness. The dynamic parameters of the vehicle are used in Ref. [9]. The fuzzy control tools in the Matlab software are then applied and designed to control the air suspensions of the vehicle under a road surface roughness of ISO level B at a speed of 20 m/s. The simulation results are shown in Fig. 4.

Fig. 3Excitation of road surface roughness according to ISO 8068 [14]

Fig. 4Control results of csemi and dynamic force of tire at second axle

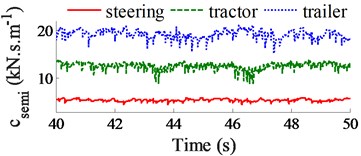
a) Semi-active damping coefficients

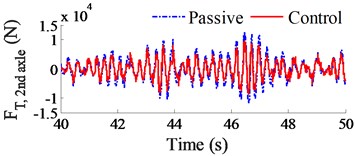
b) Dynamic tire force

Fig. 4(a) is the damping coefficients of the air suspension system at the steering, tractor, and trailer axles controlled by fuzzy control, while Fig. 4(b) is the dynamic tire force on the tractor driver axle. Similar to the research results in Ref. [9], the dynamic tire force at 2nd axle is the largest, thus, it has a great influence on road friendliness. Observing Fig. 4(b), the dynamic tire force was significantly reduced by semi-active air suspension in comparison with its passive. The calculation results in Table 3 indicate that the DLC value at 2nd axle with the control is reduced by 22.2 % compared to the passive. Besides, the RMS and MAX of dynamic tire forces ($F_{T,RMS}$ and $F_{T,MAX}$) are also significantly reduced by 23.2 % and 14.3 % in comparison with the passive. Consequently, the semi-trailer truck with semi-active air suspensions has an obvious effect on the reduction the road damage and improves the road friendliness. To fully reflect the effectiveness of semi-active air suspensions, various road surfaces are then simulated.

5.2. Control of air suspension under various road surfaces

Five road surfaces of ISO level A (very good) to ISO level E (very poor) are chosen to simulate and analyze the effect of road surface roughness on the effectiveness of semi-active air suspension system. The results of the DLC value, the $F_{T,RMS}$ and $F_{T,MAX}$ at each axle are shown in Fig. 5. It can see that all their values are significantly reduced in comparison with the passive. Moreover, the DLC value, the $F_{T,RMS}$, and $F_{T,MAX}$ at tractor driver axle are the maximum. Thus, the impact of tractor driver axle on road damage are the greatest. In Table 4, the DLC value of the tractor driver axle on road surface from ISO level A to ISO level D is from 0.03 to 0.25. Thus, the DLC value of vehicle is under normal operating conditions [15]. However, the DLC value greatly increased on ISO level E road, and its value is 0.47. In this case, the wheels of the trailer driver axle spend a significant proportion of their time disconnecting the road surface.

Fig. 5The DLC and the dynamic tire force under the various road surfaces

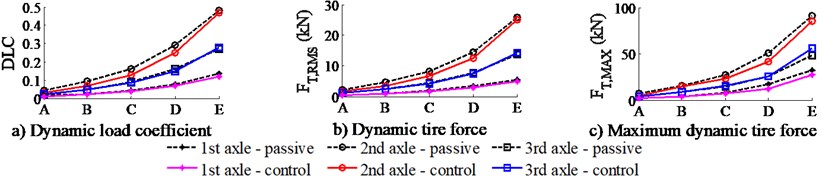
Fig. 6The dynamic tire forces on the tractor driver axle

5.3. Control of air suspension under various vehicle speeds

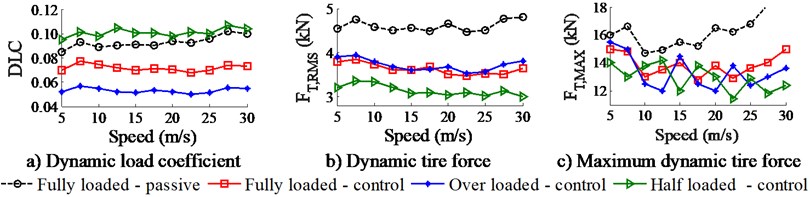
The simulation of semi-active air suspensions over a range of vehicle velocities under different loaded conditions (half loaded, fully loaded and over 50 % loaded) on ISO lever B road are plotted in Fig. 6. As shown in Fig. 6(a), under fully loaded-passive condition, the DLC value is increased with the increase of the vehicle speed. However, the DLC with semi-active air suspensions is significantly reduced. In Table 5, the maximum values of DLC at 7.5, 20, and 27.5 m/s are reduced by 17.9 %, 22.2 %, and 27.4 % respectively. Besides, the DLC also strongly depends on the loaded condition, the DLC is greatly increased in the case of the half loaded-control and it is also greatly reduced in the case of over 50 % loaded-control in comparison with the fully load-control of the trailer.

Both the $F_{T,RMS}$ and $F_{T,MAX}$ on the tractor driver axle in Fig. 10(b) and 10(c) are also significantly reduced in comparison with the passive under all different loaded conditions, especially the half loaded-control of the trailer. Table 6 also shows that the $F_{T,MAX}$at the steering, tractor driver, and trailer axles at speeds of 7.5, 20, and 27.5 m/s are significantly reduced. Especially, the maximum reduction of the $F_{T,MAX}$is greatly reduced by 10.8 %, 16.4 %, and 23 % on the tractor driver of the vehicle.