Optimal design parameters of air suspension systems for semi-trailer truck. Part 2: results and discussion

Tuan, Nguyen Van; Quynh, Le Van; Thao, Vi Thi Phuong; Duy, Le Quang

doi:10.21595/vp.2020.21563

Vibroengineering Procedia

Browse Procedia

Published: 19 October 2020

Check for updates

Optimal design parameters of air suspension systems for semi-trailer truck. Part 2: results and discussion

Nguyen Van Tuan¹

Le Van Quynh²

Vi Thi Phuong Thao³

Le Quang Duy⁴

^{1, 2, 4}Faculty of Automotive and Power Machinery Engineering, Thai Nguyen University of Technology, Thai Nguyen, Vietnam

³Faculty of International Training, Thai Nguyen University of Technology, Thai Nguyen, Vietnam

Corresponding Author:

Le Van Quynh

Cite the article Download PDF

Downloads 1008

CrossRef Citations 3

Abstract

Based on the results of model and algorithm in Part1 for searching the optimal design parameters of vehicle suspensions using genetic algorithm, in Part 2, the simulation results with MATLAB Simulink combined with an optimal program are written to search the optimal design parameters of vehicle air suspension systems in two optimal conditions. The optimal results indicate that the DLC values at all axles of vehicle respectively reduce by 9.09 %, 10.71 %, 11.11%, 10.81 %, 8.82 % (in Case 1) and 14.29 %, 19.23 %, 20.00 %, 17.14 %, 12.12 % (in Case 2) in comparison with the original air suspension systems when vehicle moves on the ISO class C road surface at $v =$ 20 m/s and full load. All these things indicate that using the genetic algorithm optimization method does not only reduce the tire dynamic loads acting on road surface but also improves the ride comfort. Finally, the optimum performance of vehicle suspension systems is considered and reassessed under different operating conditions. The evaluation results indicate that the optimum performance of the air suspension systems has better potential to improve the road friendliness which provides a ride comfort for road surfaces and vehicle.

Optimal design parameters of air suspension systems for semi-trailer truck. Part 2: results and discussion

Highlights

The geometric parameters of the air springs of suspension systems are optimized by genetic algorithm.
The design parameters of the air suspension systems are optimized by genetic algorithm.
The simulation results with MATLAB Simulink combined with an optimal program are written to search the optimal design parameters of vehicle air suspension systems in two optimal conditions.

1. Introduction

In order to improve the performance of the air suspension system for reducing the negative impact on the road surface, the control and optimization methods for air suspension systems are discussed in some of the following studies such as the control methods: the genetic LQG and PID control were used to control an air suspension system [1], the performance of the air suspension system of heavy trucks was analyzed with semi-active fuzzy control [2] and the two-bag air suspension system for heavy-duty vehicles was analyzed using the multi-body vehicle model [3], the optimization technique available in OptiY with SIMULINK simulation was used to search the optimal parameters of air spring of suspension system using vehicle dynamic model with 2 d.o.f [4], The air suspension system with independent height and stiffness tuning was analyzed and the geometric parameters of air spring were optimized [5], the glowworm swarm optimization proportional-integral-derivative controlling algorithm was designed to optimize magnetorheological damper for air suspensions [6], the vehicle suspension parameters of non-linear air spring was analyzed and optimized by using the multi-objective optimization method [7], and the optimization of suspension geometric parameters was analyzed and optimized using a double-loop multi-objective particle swarm optimization algorithm (DL-MOPSO) when the vehicle operates under various driving conditions [8]. The optimal parameters of the suspension systems as well as drum’s isolation system were found out using genetic algorithm (GA) [9, 10]. Based on the results of model and algorithm in Part 1, the rest of this paper of Part 2 is organized as follows: Optimization of suspension parameters and discussion are presented in Section 2. Section 3 presents the efficiency of the optimal design parameters compared with the original design parameters of air suspension systems under the different vehicle operating conditions and the conclusions are given in Section 4.

2. Optimization of suspension parameters and discussion

In order to find the optimal design parameters for the air suspension systems of the articulated truck semi-trailer, Matlab/Simulink software is used to simulate the half-vehicle dynamic model with a set of parameters of the articulated truck semi-trailer in Table 1 when the vehicle moves on the ISO class C road surface at $v =$ 20 m/s and full load.

Table 1Parameters of the 5-axle semi-trailer truck

Parameters	Values	Parameters	Value	Parameters	Values
$k_{t 1}$ / (N.m^-1)	647500	$k_{k}$ / (N.m^-1)	2000000	$I_{c}$ / kg.m²	2056
$k_{t 2}$ / (N.m^-1)	1185000	$k_{s}$ / (N.m^-1)	28500	$l_{1}$ / m	2.741
$k_{t 3}$ / (N.m^-1)	1185000	$c_{k}$ / (N.s.m^-1)	200000	$l_{2}$ / m	2.229
$k_{t 4}$ / (N.m^-1)	1185000	$c_{s}$ / (N.s.m^-1)	9200	$l_{3}$ / m	3.334
$k_{t 5}$ / (N.m^-1)	1185000	$m_{a 1}$ / kg	584	$l_{4}$ / m	1.330
$c_{t 1}$ / (N.s.m^-1)	258.50	$m_{a 2}$ / kg	735	$l_{5}$ / m	2.960
$c_{t 2}$ / (N.s.m^-2)	325.00	$m_{a 3}$ / kg	735	$l_{6}$ / m	5.620
$c_{t 3}$ / (N.s.m^-1)	325.00	$m_{a 4}$ / kg	735	$l_{7}$ / m	2.685
$c_{t 4}$ / (N.s.m^-1)	325.00	$m_{a 5}$ / kg	735	$l_{8}$ / m	1.115
$c_{t 5}$ / (N.s.m^-1)	325.00	$m_{b 1}$ / kg	3783	$l_{9}$ / m	0.235
$c_{1}$ / (N.s.m^-1)	11270	$m_{b 2}$ / kg	24800	$l_{10}$ / m	1.200
$k_{c 1}$ / (N.m^-1)	33860	$m_{c}$ / kg	1208	$α_{2,3}$	0.0708
$k_{c 2}$ / (N.m^-1)	33860	$m_{s}$ / kg	116	$α_{4,5}$	0.0481
$c_{c 1}$ / (N.s.m^-1)	3650	$I_{b 1}$ / kg.m²	45819	$β_{2,3}$	0.0223
$c_{c 2}$ / (N.s.m^-1)	3650	$I_{b 2}$ / kg.m²	195820	$β_{4,5}$	0.0399

Operation parameters of genetic algorithm as follows: The population size is 100; The number of generations is 200; Elitism: best seven individuals from each generation were chosen for creation of next population; Mutation: random and adaptive mutations were used; Crossover: just neighboring individuals were crossed; and selection: random [9]. A genetic algorithm program in Matlab are called by Simulink module function using the sim function, the simulation results are calculated after the calculation of the population of the objective function value. The optimal values of the parameters of air suspension systems are obtained by genetic algorithms method in comparison with the original design parameters of air suspension systems with two cases, as shown in Table 2 and Table 3.

Table 2GA optimization results in Case 1

Air spring suspension parameters	Initial design parameters	GA optimization
Case 1 Optimal design of geometrical parameters of air spring suspension systems
$A_{02}$ / m²	0.085	0.010
$A_{03}$ / m²	0.085	0.016
$V_{02}$ / m³	0.028	0.003
$V_{03}$ / m³	0.028	0.005
$p_{02}$ / MPa	0.692	0.428
$p_{03}$ / MPa	0.692	0.528
$A_{04}$ / m²	0.092	0.041
$A_{05}$ / m²	0.092	0.032
$V_{04}$ / m³	0.03	0.014
$V_{05}$ / m³	0.03	0.011
$p_{04}$ / MPa	0.492	0.254
$p_{05}$ / MPa	0.492	0.260

Table 3GA optimization results in Case 2

Case 2 Optimal design of parameters of air suspension systems
$A_{02}$ / m²	0.085	0.013
$A_{03}$ / m²	0.085	0.021
$V_{02}$ / m³	0.028	0.004
$V_{03}$ / m³	0.028	0.007
$p_{02}$ / MPa	0.692	0.243
$p_{03}$ / MPa	0.692	0.304
$A_{04}$ / m²	0.092	0.069
$A_{05}$ / m²	0.092	0.032
$V_{04}$ / m³	0.03	0.023
$V_{05}$ / m³	0.03	0.011
$p_{04}$ / MPa	0.492	0.287
$p_{05}$ / MPa	0.492	0.337
$c_{2}$ / (N.s.m^-1)	26500	53000
$c_{3}$ / (N.s.m^-1)	26500	66300
$c_{4}$ / (N.s.m^-1)	38000	24700
$c_{5}$ / (N.s.m^-1)	38000	20900

The optimal results of the DLC values at 1st, 2nd, 3rd, 4th and 5th axles of vehicle in comparison with those original results with two cases are shown in Table 4. It is indicated from Table 4 that the DLC values of the optimal design parameters of air suspension systems at all axles of vehicle respectively reduce by 9.09 %, 10.71 %, 11.11 %, 10.81 %, 8.82 % (in Case 1) and 14.29 %, 19.31 %, 20.00 %, 17.14 %, 12.12 % (in Case 2) in comparison with the original air suspension systems.

All these things indicate that using this genetic algorithm optimization method does not only reduce the tire dynamic loads acting on road surface but also improves the ride comfort.

Table 4Comparison of optimized results

Parameters and indexes	DLC_t1	DLC_t2	DLC_t3	DLC₄	DLC_t5
Case 1 Optimal design of geometrical parameters of air spring suspension systems
Before optimization	0.024	0.031	0.030	0.041	0.037
After optimization	0.022	0.028	0.027	0.037	0.034
Decrease %	9.09	10.71	11.11	10.81	8.82
Case 2 Optimal design of parameters of air suspension systems
Before optimization	0.024	0.031	0.030	0.041	0.037
After optimization	0.021	0.026	0.025	0.035	0.033
Decrease %	14.29	19.23	20.00	17.14	12.12

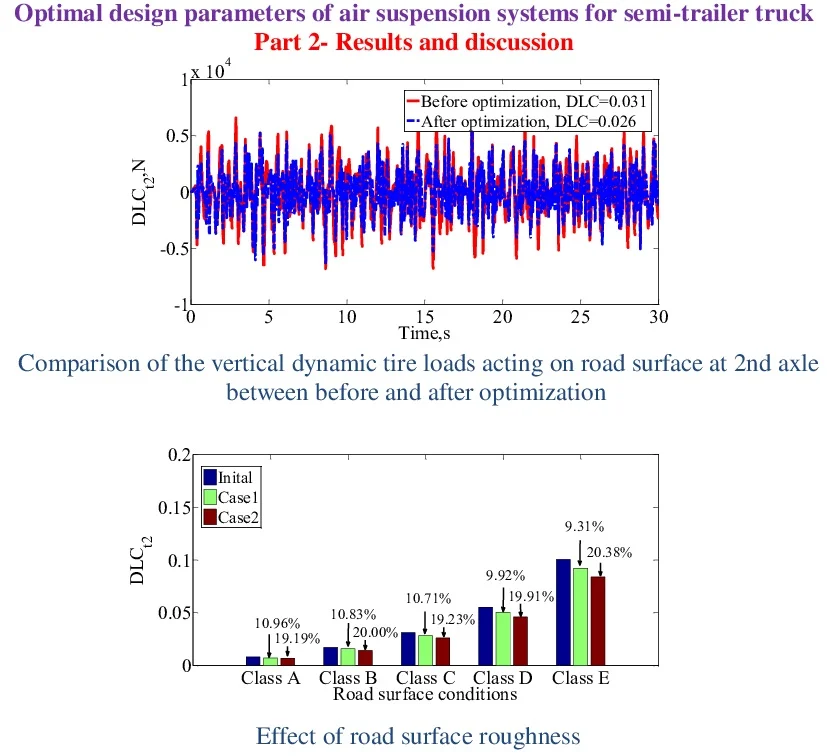
The comparison of optimized results of the vertical dynamic tire loads acting on road surface in time domain response at 2nd axle in case 1 and 4th axle in case 2 are show Fig. 1 and Fig. 2. The results from Fig. 1 and Fig. 2 show that the performance optimization of the air suspension systems with two cases is better than the original air suspension systems for reducing the negative impact on road surface, especially when the optimum design parameters of the air suspension systems in case 2.

3. Different operating conditions of vehicle

To evaluate the performance of the optimal design parameters of the air suspension systems on road surface friendliness, the different operating conditions such as road surface roughness, vehicle speed and vehicle load [11-15] are analyzed respectively in this paper.

Fig. 1Comparison of the vertical dynamic tire loads acting on road surface at 2nd axle in case 1 between before and after optimization

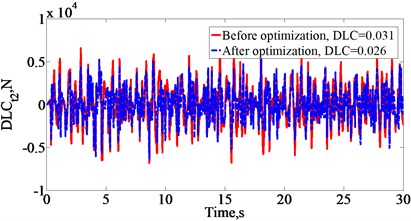
Fig. 2Comparison of the vertical dynamic tire loads acting on road surface at 4th axle in case 2 between before and after optimization

3.1. Effect of road surface roughness

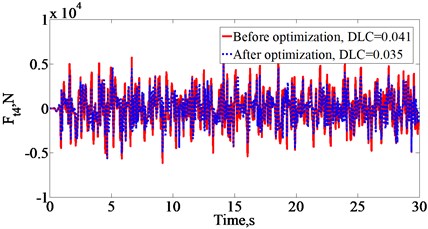
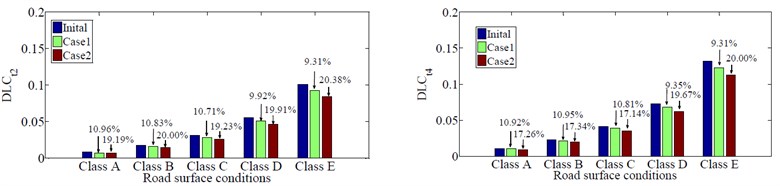
To evaluate the performance of the optimal design parameters of the air suspension systems in comparing with the original design parameters for reducing the negative impact on road surface with two cases, five road conditions from ISO class A (very good) to ISO class E (very poor) are used when vehicle moves at the vehicle speed of 20 m/s and full load. The DLC values at 2nd and 4th axles of vehicle with three cases are shown in Fig. 3(a). Fig. 3(a) shows that the DLC values at 2nd and 4th axles of vehicle with the optimal design parameters of air suspension system in case 1 respectively reduce by 10.96 %, 10.83 %, 10.71 %, 9.92 %, 9.31 % and 10.92 %, 10.95 %, 10.81 %, 9.35 %, 9.31 % in comparison with the original air suspension systems of vehicle. Similarly, the DLC values at 2ndand 4th axles of vehicle significantly reduce by 19.19 %, 20.00 %, 19.23 %, 19.91 %, 20.38 % and 17.26 %, 17.34 %, 17.14 %, 19.67%, 20.00 %, respectively in Case 2.

3.2. Effect of vehicle speed

The vehicle speeds of 5 m/s, 10 m/s, 15 m/s, 20 m/s and 25 m/s are considered to evaluate the performance of the optimal design parameters of the air suspension systems with two cases for a 5- axle semi-trailer truck when vehicle moves on the road surface condition of the ISO class C and full loaded. The DLC values at 2nd and 4th axles of vehicle with three cases are shown in Fig. 3(b), indicating that the optimal results have a significant improvement in road-friendly level in comparison with the original air suspension systems of vehicle at all vehicle speeds. Moreover, the DLC values at 2ndand 4th axles of vehicle with the optimal design parameters of air suspension system in the optimal results in case 2 are reduced by 6.14 %, 9.23 %, 7.95 % and 4.12 %, 2.31 %, 6.33 %, respectively in comparison with Case 1 when the vehicle speed increases from 10 to 15 m/s, and then to 20 m/s. The DLC values increase or decrease in abnormal manner in each of the vehicle speed because the vehicle speed affects the product of vehicle speed and the cutoff values of the roughness spatial frequency [16].

Fig. 3Comparing of the DLC values at 2nd and 4th axles of vehicle with three cases

a) Effect of road surface roughness

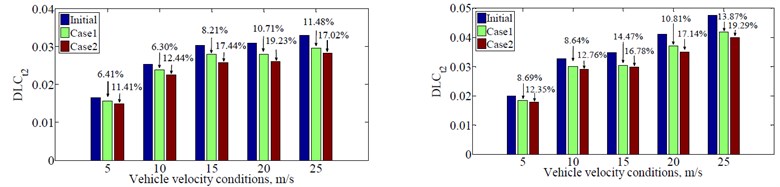
b) Effect of vehicle speed

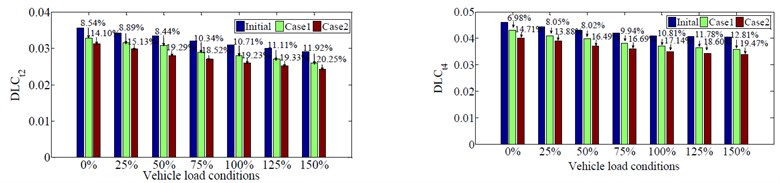
c) Effect of vehicle load

3.3. Effect of vehicle load

To continue evaluating the optimal design parameters of the air suspension systems in comparing with the original design parameters for reducing the negative impact on road surface with two cases, seven load conditions of vehicle from 0 % (empty load) to 150 % (over 150 %) are used when vehicle moves on the road surface condition of the ISO class C and the vehicle speed of 20 m/s. The DLC values at 2nd and 4th axles of vehicle with three cases are shown in Fig. 3(c). Fig. 3(c) shows that the DLC values at 2nd and 4th axles of vehicle with the optimal design parameters of air suspension system in case 2 significantly reduce by 14.10 %, 15.13 %, 19.29 %, 18.52 %, 18.31 %, 19.33 %, 20.25 % and 14.71 %, 13.88 %, 16.49 %, 16.69 %, 17.14 %, 18.86 %, 19.41 %, respectively in comparison with the original air suspension systems of vehicle. Moreover, the values of DLC at 2nd and 4th axles of vehicle increase the fastest when vehicle move under 50 % load condition and this problem has a negatively effect on road surface. However, when the vehicle's load increases over 75 % vehicle load, the values of DLC at 2nd and 4th axles of vehicle reduce gradually, which has a benefit effect on road surface. However, it has no benefit on the durability of the part of vehicle and the safe movement of vehicle [17].

4. Conclusions

In part 2 of this study, the simulation results by using MATLAB Simulink combined with an optimal program is written to solve the optimization problem of nonlinear air suspension parameters in two optimal conditions. The obtained the optimization results show that the DLC values of the optimal design parameters of air suspension systems at all axles of vehicle reduce in comparison with the initial air suspension systems of vehicle when vehicle moves on the ISO class C road surface at $v =$ 20 m/s and full load. Especially, the DLC values of the optimal design parameters of air suspension systems at 1st, 2nd, 3rd 4th and 5th axles of vehicle considering case 2 respectively reduce by 4.76 %, 7.69 %, 8.00 %, 5.71 % and 3.03 % in comparison in Case 1. Finally, the optimum performance of vehicle suspension systems is considered and evaluated again under different operating conditions and the obtained optimization results indicated that the optimum performance is the significant reduction the tire loads and road surface damage. The study results can be used for the searchers, vehicle manufacturers and traffic managers for further considerations during design as well as perfect design in the design of vehicle air suspension systems.

References

Tang Chuan Yin, Li Yun Gong Research on air suspension system based on genetic LQG and PID control. International Conference on Optics, Electronics and Communications Technology, 2017.

Publisher
Nguyen V., Zhang J., et al. Performance analysis of air suspension of heavy truck with semi-active fuzzy control. Journal of Southeast University (English Edition), Vol. 33, Issue 2, 2017, p. 159-165.

Search CrossRef
Tajima J., Momiyama F., Yuhara N. A new solution for two-bag air suspension system with leaf spring for heavy-duty vehicle. Vehicle System Dynamics, Vol. 44, Issue 2, 2006, p. 107-138.

Publisher
Abid H. J., Chen J., Nassar A. A. Equivalent air spring suspension model for quarter-passive model of passenger vehicles. International Scholarly Research Notices, Vol. 2015, 2015, p. 974020.

Publisher
Karimi Eskandary P., Khajepour A., Wong A., Ansari M. Analysis and optimization of air suspension system with independent height and stiffness tuning. International Journal of Automotive Technology, Vol. 17, Issue 5, 2016, p. 807-816.

Publisher
Xiao P., Gao H., Shi P., Niu L. Research on air suspension with novel dampers based on glowworm swarm optimization proportional-integral-derivative algorithm. Advances in Mechanical Engineering, Vol. 10, Issue 8, 2018, https://doi.org/10.1177/1687814018791710.

Publisher
Li J. H., He J., Li X. H. Multi-Objective optimization of vehicle air suspension based on Simulink-Mfile mixed programming. Applied Mechanics and Materials, Vol. 509, 2014, p. 63-69.

Publisher
Yikai Chen, Sen Huang, Lloyd Davis, et al. Optimization of geometric parameters of longitudinal-connected air suspension based on a double-loop multi-objective particle swarm optimization algorithm. Applied Sciences, Vol. 8, Issue 9, 2018, p. 1454.

Publisher
Goga V., Kľúčik M. Optimization of vehicle suspension parameters with use of evolutionary computation. Procedia Engineering, Vol. 48, 2012, p. 174-179.

Publisher
Quynh L. V., Thao V. T. P., Phong T. T. Optimal design parameters of drum’s isolation system for a double-drum vibratory roller. Vibroengineering Procedia, Vol. 31, 2020, p. 74-79.

Publisher
Le V. Q. Comparing the performance of suspension system of semi-trailer truck with two air suspension systems. Vibroengineering Procedia, Vol. 14, 2017, p. 220-226.

Publisher
Long L. X., Hong T. T., et al. Performance analysis of the hydro-pneumatic suspension system of heavy truck. International Journal of Mechanical Engineering and Technology, Vol. 9, Issue 13, 2018, p. 1128-1139.

Search CrossRef
Van Cuong B., Van Quynh L., Long L. X. Influence of heavy truck operating condition on dynamic load coefficient. Advances in Engineering Research and Application, 2018, p. 372-379.

Publisher
Long L. X., Quynh L. V., Cuong B. V. Study on the influence of bus suspension parameters on ride comfort. Vibroengineering Procedia, Vol. 21, 2018, p. 77-82.

Publisher
Van Quynh L. Influence of semi-trailer truck operating conditions on road surface friendliness. Vibroengineering Procedia, Vol. 16, 2017, p. 67-72.

Publisher
Shi X. M., Cai C. S. Simulation of dynamic effects of vehicles on pavement using a 3D interaction model. Journal of Transportation Engineering, Vol. 135, Issue 10, 2009, p. 736-744.

Publisher
Le V. Q., Zhang J., Liu X., Wang Y. Nonlinear dynamic analysis of interaction between vehicle and road surfaces for 5-axle heavy truck. Journal of Southeast University, Vol. 27, Issue 4, 2011, p. 405-409.

Search CrossRef

Cited by

Advances in Engineering Research and Application

Le Xuan Long | Dang Viet Ha | Nguyen Van Tuan | Vu Thanh Niem | Vu Thi Hien

(2023)

Advances in Engineering Research and Application

Ta Tuan Hung | Le Xuan Long | Nguyen Van Tuan | Hoang Anh Tan | Vu The Truyen

(2023)

Optimal selection for an air suspension system on buses through a unique high level parameter in genetic algorithms

Truong Manh Hung

(2022)

About this article

Received

25 June 2020

Accepted

09 August 2020

Published

19 October 2020

SUBJECTS

Mathematical models in engineering

DOI

https://doi.org/10.21595/vp.2020.21563

Keywords

semi-trailer truck

air suspension system

dynamic load coefficient

genetic algorithm

optimal parameters

road friendliness

Acknowledgements

This research was supported financially by Thai Nguyen University of Technology, TNUT, Viet Nam.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 03 13

Improving ride comfort and road friendliness of heavy truck using semi-active suspension system

Hao Li, Vanliem Nguyen

Research article

2020 11 26

Control of the air suspension system of semi-trailer trucks to enhance the road friendliness

Huaxiang Zhou, Xiaoyan Wu, Peiling Wang

Research article

2020 10 19

Optimal design parameters of air suspension systems for semi-trailer truck. Part 1: modeling and algorithm

Nguyen Van Tuan, Le Van Quynh, Vi Thi Phuong Thao, Le Quang Duy

Research article

2018 12 13

Evaluating the effect of the working conditions on the ride comfort and road friendliness of the heavy truck

Van Liem Nguyen, Khac Tuan Nguyen

N. V. Tuan, L. V. Quynh, V. T. P. Thao, and L. Q. Duy, “Optimal design parameters of air suspension systems for semi-trailer truck. Part 2: results and discussion,” Vibroengineering PROCEDIA, Vol. 33, pp. 147–152, Oct. 2020, https://doi.org/10.21595/vp.2020.21563

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2020.21563
UR  - https://doi.org/10.21595/vp.2020.21563
TI  - Optimal design parameters of air suspension systems for semi-trailer truck. Part 2: results and discussion
T2  - Vibroengineering PROCEDIA
AU  - Quynh, Le Van
AU  - Tuan, Nguyen Van
AU  - Thao, Vi Thi Phuong
AU  - Duy, Le Quang
PY  - 2020
DA  - 2020/10/19
PB  - JVE International Ltd.
SP  - 147-152
VL  - 33
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Quynh_2020,
	doi = {10.21595/vp.2020.21563},
	url = {https://doi.org/10.21595/vp.2020.21563},
	year = 2020,
	month = {oct},
	publisher = {{JVE} International Ltd.},
	volume = {33},
	pages = {147--152},
	author = {Le Van Quynh and Nguyen Van Tuan and Vi Thi Phuong Thao and Le Quang Duy},
	title = {Optimal design parameters of air suspension systems for semi-trailer truck. Part 2: results and discussion},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]L. V. Quynh, N. V. Tuan, V. T. P. Thao, and L. Q. Duy, “Optimal design parameters of air suspension systems for semi-trailer truck. Part 2: results and discussion,” Vibroengineering PROCEDIA, vol. 33, pp. 147–152, Oct. 2020, doi: 10.21595/vp.2020.21563.

Copy IEEE

Copied to clipboard!

Quynh, Le Van, Nguyen Van Tuan, Vi Thi Phuong Thao, and Le Quang Duy. “Optimal Design Parameters of Air Suspension Systems for Semi-Trailer Truck. Part 2: Results and Discussion.” Vibroengineering PROCEDIA 33 (October 19, 2020): 147–52. https://doi.org/10.21595/vp.2020.21563.

Copy Chicago

Copied to clipboard!

Optimal design parameters of air suspension systems for semi-trailer truck. Part 2: results and discussion

Abstract

Highlights

1. Introduction

2. Optimization of suspension parameters and discussion

3. Different operating conditions of vehicle

3.1. Effect of road surface roughness

3.2. Effect of vehicle speed

3.3. Effect of vehicle load

4. Conclusions

References

Cited by

About this article

Related Articles