Abstract
The vibration signal of rolling bearing often has the characteristics of strong noise, nonlinearity and non-stationary, so the accurate fault feature information cannot be obtained directly from the measured vibration signal. Therefore, a fault pattern recognition method for rolling bearing based on complete ensemble local mean decomposition with adaptive noise (CELMDAN) and fuzzy entropy is deeply studied. Firstly, the reason of modal aliasing existing in local mean decomposition (LMD) method is explained. According to the previous methods for modal aliasing processed in other methods, CELMDAN method is proposed. The experiment proves that the proposed CELMDAN method can better handle the vibration signals with nonlinear and non-stationary. Then, the principle and properties of the fuzzy entropy are introduced in detail, and the fault feature of rolling bearing can be reflected. Finally, extreme learning machine (ELM) is introduced as the pattern recognition method based on the effective fault feature of rolling bearing. Combined with the verification of experimental signal, it is proved that the proposed method can extract the fault features of rolling bearing accurately and effectively, and the fault pattern recognition of rolling bearing can be realized.
1. Introduction
Rolling bearing is widely used in the rotating machinery such as rail vehicle, lifting equipment and so on [1]. With the development of technology and the continuous expansion of modern production, it is developing in the direction of large-scale, complex and precise, and its number is growing rapidly, which results the fault probability of rotating machinery rise rapidly [2]. According to the statistics, 30 % of the faults in rotating machinery are caused by the damage of rolling bearing, and it is of great significance to study the fault pattern recognition for rolling bearing [3]. When rolling bearing fails, the measured vibration signal is usually complex, so the feature extraction and pattern recognition occupy a critical position in the analysis of vibration signal [4].
In the aspect of feature extraction of vibration signals, the main idea is to quantize the fault feature after decomposing the original vibration signal, and empirical mode decomposition (EMD) is widely used. However, EMD has many problems in analyzing the vibration signal of fault rolling bearing. For example, the modal aliasing results the intrinsic functions with different frequencies are decomposed into the same scale, and affects the practicability of EMD. As a new time-frequency analysis method, local mean decomposition (LMD) has certain advantages compared with EMD. Especially from the perspective of algorithm steps and calculation results, the superiority of LMD can be highlighted, and the main advantages include as follows: (1) The signal local fluctuations can be reflected more accurately by product function (PF) components; (2) There are no problems of over enveloping and unenveloping; (3) Less endpoint effects and more accurate instantaneous frequencies. However, LMD also decomposes the vibration signal into a series of PF components from high-frequency to low-frequency, which is like EMD. Ideally, each PF component should be a single component signal, but in actually, a certain PF signal component will contain the features with multiple time-scales, and a certain feature with same time-scale will also be decomposed into multiple PF components. The modal aliasing is mainly caused by the high frequency intermittent signal [5]. It directly causes the PF component not to correspond to the original signal, so that its time-frequency distribution has no physical meaning. The direct result is that the PF components are not correspond to the original vibration signal, which makes the time-frequency distribution of the PF component not have physical significance. For the widely applied method: EMD and LMD, their improved algorithms for modal aliasing and endpoint effect have been proposed one after another. Wang [6] applied the polynomial fitting method to the signal endpoints fitting. Xu [7] proposed the image extension method to solve the endpoint problem. For the modal aliasing problem, some predecessors tried to solve such problems by adding Gaussian white noise, and ensemble empirical mode decomposition (EEMD) was proposed under the guidance of such ideas. However, the problem of reconstruction error and incomplete decomposition process are reflected. For those problems, complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) is proposed and has achieved good results. Bouhalais [8] proposed a hybrid method based on CEEMDAN and an optimized wavelet multi-esolution analysis for the detection of rolling bearing faults under variable speed. The CEEMDAN was used in order to select the oscillatory mode that best reflect the impulsive form of the defected bearing signal. Vanraj [9] described and presented the implementation of CEEMDAN for fault diagnosis of simulated local defects using sound signals in a fixed-axis gearbox. By extracting statistical parameters from decomposed sound signals for different simulated faults, more accurate IMFs and fault severity were obtainwd. Therefore, based on predecessors’ research, this paper proposed the CELMDAN algorithm, which combines CEEMDAN and LMD [10]. By adding the decomposed noise signal, it is used to reduce the influence of modal aliasing. It is a PF component reconstruction problem of LMD. Further, it is the key to quantify the fault features contained in the decomposition results of CELMDAN. Some feature indexes are often used, such as mean value, root mean square, peak value and frequency center of gravity, but they are more suitable for representing stationary signals. Entropy is a physical quantity that expresses the disorder degree of molecular state in thermodynamics at first. After further research by scholars, it is applied to reflect the complexity and stability of signals, and the feature of non-stationary signals can be quantified. Entropy can be understood as the probability of occurrence of certain information. The more orderly a system is, the lower the entropy is. The more chaotic the system is, the greater the entropy is. When the mechanical vibration signal is disturbed by the impact of the fault, a new signal component is added to the original signal, and the complexity and stability of the entire signal change. This corresponds to the generation of new patterns in the definition of entropy. The more new patterns are generated in the signal, the greater the entropy value, that is, the greater the complexity of the original signal, the worse the stability. And fuzzy entropy [11] is a typical and effective feature which can be used as the measurement value that reflects the complexity of time series, so it can be used as the sensitive feature of vibration signals of rolling bearing.
In the aspect of pattern recognition, the fault recognition technology based on mathematical model is the core of fault diagnosis and usually more precise [12-14]. Due to the powerful learning and recognition ability, neural networks are excellent pattern recognition model and have been widely used in the field of fault diagnosis of rolling bearing [15]. Extreme learning machine (ELM) is a new neural network algorithm based on single hidden layer. The weights and thresholds among input layer, output layer and hidden layer can be randomly generated. In the training process, only the number of neurons in hidden layer needs to be set, and no other parameters need to be adjusted. It has the advantages of simple parameter selection, fast learning speed and good generalization ability, and has attracted more and more attention and application.
Therefore, in this paper, the vibration signal is decomposed by CELMDAN, then, the fuzzy entropy values of effective PF components are extracted to construct the training and testing samples. Finally, the fault pattern recognition of rolling bearing is performed through the trained ELM [16].
2. Model establishment
2.1. CELMDAN
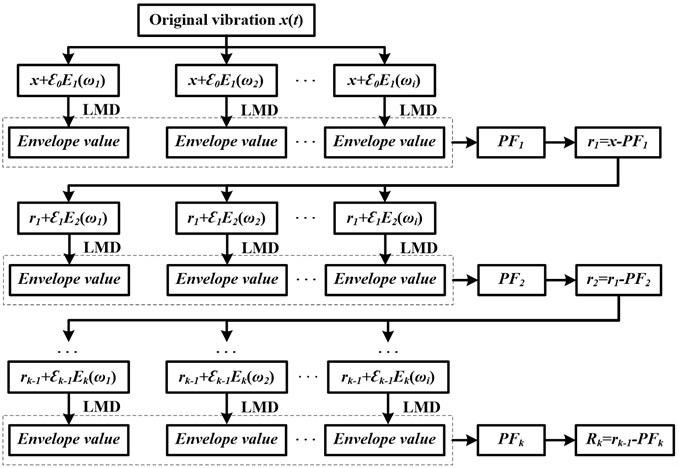
CELMDAN is proposed based on the research idea of LMD and CEEMDAN. The following formulas are the decomposition process of CELMDAN. Firstly, the operator Ej(⋅) is defined, which represents the j-th PF component of the LMD. Assuming that wi is the white noise with normal distribution, i represents the times of the added noise. εk is the amplitude coefficient of white noise. Assuming that the original signal to be decomposed is x(t), and its decomposition process is as follows [10, 17]:
(1) The original signal adding white noise is x(t)+ε0wi(t), and it is decomposed by LMD, and the average of all the first order PF components is defined as the final first PF component. That is as follows:
(2) The remaining signal r1 after screening out the first order PF component is as follows:
(3) For r1(t)+ε1E1(wi(t)), i=1,2,...,I, LMD is carried out. The average of all first order PF components is defined as the final second PF component, and that is as follows:
(4) For k=2,⋯,K, the k-th remaining signal is as follows:
(5) For rk(t)+εkEk(wi(t)), i=1,2,...,I, LMD is continued, Furthermore, the average of all first order PF components can be still obtained:
(6) Repeat steps (4) and (5) until the residual component does not satisfy the decomposition condition, then, the decomposition process is completed. The last residual component can be expressed as follows:
where K is the total amount of final PF components, and the original signal can be expressed as follows:
The following is the flowchart of CELMDAN algorithm.
Fig. 1The flowchart of CELMDAN algorithm
2.2. Fuzzy entropy
From the perspective of the analysis of vibration signals, feature extraction and pattern recognition occupy a critical position, and that are the core of fault diagnosis. When the rolling bearing fails, the measured vibration signal is often complex. The fuzzy entropy can be used as the measurement value that reflects the complexity of time series, so it can be used as the sensitive feature of vibration signals. Therefore, in this paper, the vibration signal is decomposed by CELMDAN, then, the fuzzy entropy values of each effective PF components are extracted to construct the training and testing samples. Finally, the fault pattern recognition of rolling bearing is performed through the trained ELM [16].
Define a discrete sequence {x(k),k=1,2,⋯,N}, and these elements are reconstructed in order. m is the embedded dimension, and the following can be obtained [18]:
where i=1,2,⋯,N-m+1, x0(i) is the mean of [x(i),x(i+1),…,x(i+m-1)], and it can be expressed as follows:
The d(i,j) is defined as the distance between X(i) and X(j), which is the largest difference between the two elements. Then find its absolute value:
where k=1,2,⋯,m-1, i,j=1,2,⋯,N-m+1.
The fuzzy membership function μ(x,r) is defined to measure the complexity of the sequence, and the similarity Dij between the vectors X(i) and X(j) is defined as follows:
where σ is the standard deviation of the sequence, r∈(0,1).
And then, the function is defined as follows:
The new embedding dimension is set as m=m+1, and above steps are repeated, and that can be obtained as follows:
where N is the length of the data, m is the embedded dimension, and r is the parameter of the used fuzzy membership function. Therefore, the fuzzy entropy can be defined as follows:
In the actual calculation process, the length of sequence is finite, so the fuzzy entropy can be defined as follows:
It can be seen from the algorithm of fuzzy entropy that the sequence mean is introduced in the sequence reconstruction process. When the data is fluctuating, the similarity of the fuzzy entropy is no longer determined by the absolute mean, and the stability of the calculation result is greatly enhanced. Meanwhile, the similarity measure method in calculation process of fuzzy entropy adopts the exponential metric method, due to the continuity of this function is better, so the fuzzy entropy value will also change smoothly. Therefore, the fuzzy entropy is selected in this paper as the fault feature of the vibration signal of rolling bearing. On the basis of the extracted fault feature, the fault pattern recognition of rolling bearing can be finally realized by the combining ELM which has the significant advantages in recognition.
3. The introduction of experimental platform
This experiment adopts the mechanical fault comprehensive simulation test bench of Spectra Quest of the United States. The test bench is connected in turn by inverter, motor, coupling, fault simulator, etc. The acceleration signal and the rotational speed value during the operation are collected by the data acquisition instrument, and the used experimental platform is shown in Fig. 2, and the bearing pedestal and rolling bearing are shown in Fig. 3. The setting condition of experiment process is shown in Table 1.
Table 1The setting conditions of experiment process
Motor speed | Sampling frequency | System load | Sample length |
1800 r/min | 10000 | 5 Nm | 4096 |
Fig. 2Experimental platform

Fig. 3Bearing pedestal and rolling bearing

4. The analysis of experimental results
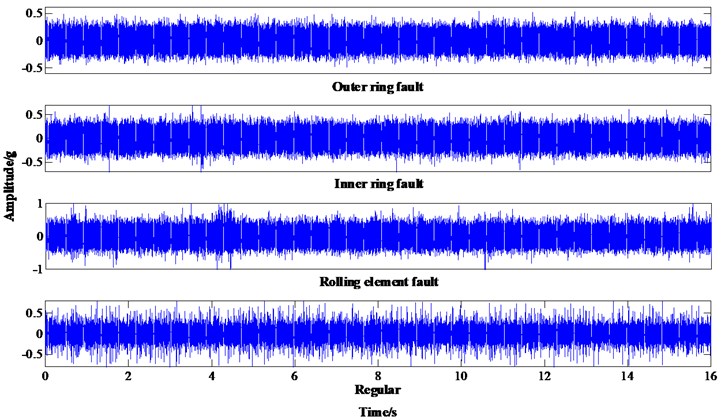
In order to verify the effectiveness of the proposed method in this paper, four types of rolling bearing vibration signals (Regular, outer ring fault, inner ring fault, rolling element fault) are selected for analysis. The time domain waveforms of the vibration signals are shown in Fig. 4.
Fig. 4The time domain waveforms of the vibration signals
In the experiment of this paper, 60 groups of samples were intercepted from each type of vibration signals, and each group of samples included 4096 data points. The obtained 4×60 groups of samples are processed by CELMDAN. The first 5 PF components with higher correlation with the original vibration signal are selected to calculate the fuzzy entropy. The fuzzy entropy matrix with 5×240 dimension can be obtained by decomposing all 240 groups of samples, and each type of vibration signal should obtain a fuzzy entropy matrix with 5×60 dimension. Generally speaking, the more training samples, the more data information can be used, and that is more conducive to the establishment of fault diagnosis model. But if the training samples are excessive, it is also easy to cause the over-fitting problem of fault diagnosis model. However, it is difficult to obtain enough samples of various rolling bearing states, and the available samples are limited under actual conditions. Therefore, based on previous research experience, 60 % of the samples can be selected as training samples, and 40 % as testing samples. It not only can complete the training of fault diagnosis model based on limited samples, but also can have some testing samples to evaluate the performance of the trained diagnosis model. In this paper, each rolling bearing state has 60 samples by the experiment, so the first 35 groups of samples of each type fuzzy entropy matrix are selected to train the ELM model, and the last 25 groups of samples of each type fuzzy entropy matrix are used for testing. Due to space limitations, only one sample of each type is selected for explanation. The decomposition results of CELMDAN for each group of sample are shown in Fig. 5- Fig. 8. The fuzzy entropy values obtained from each samples are shown in Table 2.
Fig. 5The first five PF components of the vibration signal of regular
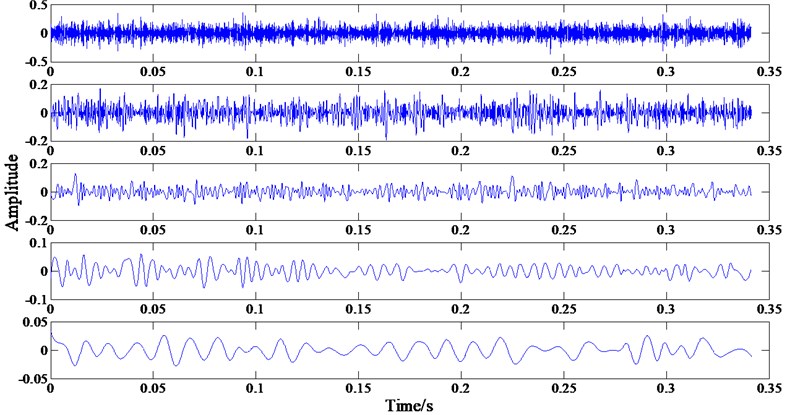
Fig. 6The first five PF components of the vibration signal of outer ring fault
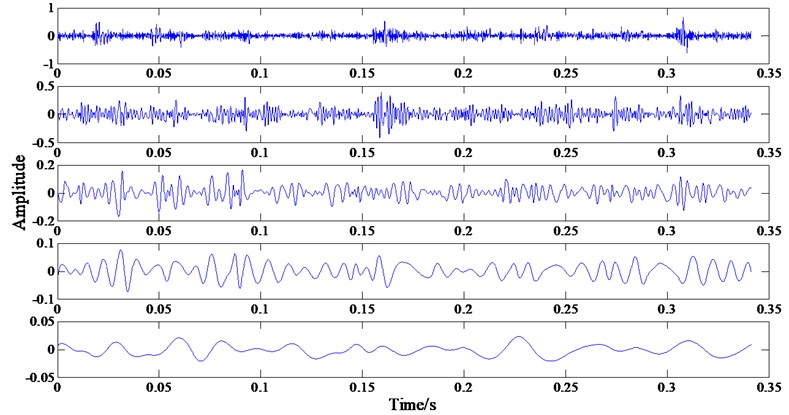
Fig. 7The first five PF components of the vibration signal of inner ring fault
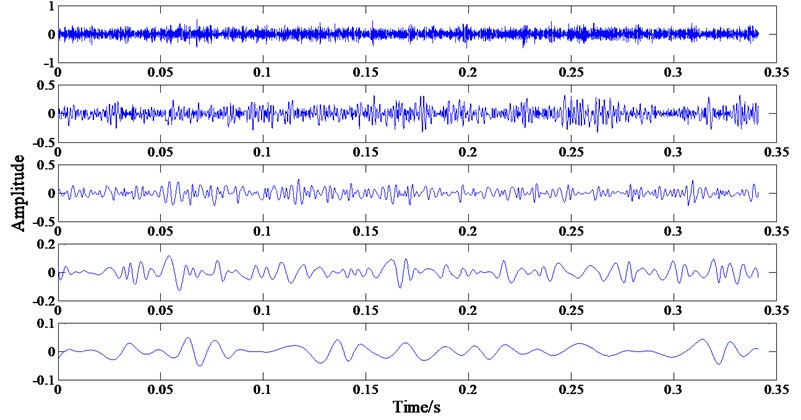
Fig. 8The first five PF components of the vibration signal of rolling element fault
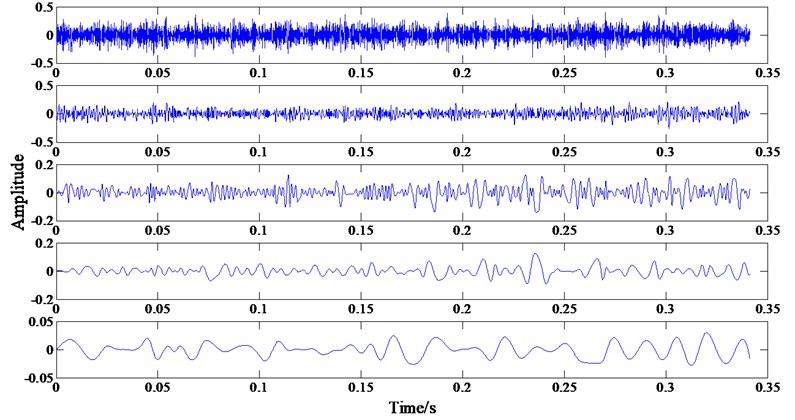
Table 2Fuzzy entropy values obtained from the samples of different rolling bearing states
Rolling bearing state | Fuzzy feature values | ||||
PF1 | PF2 | PF3 | PF4 | PF5 | |
Regular | 0.0632 | 0.0274 | 0.0032 | 1.920e-4 | –2.119e-4 |
Outer ring fault | 0.1077 | 0.0254 | 0.0054 | 4.069e-4 | –1.943e-4 |
Inner ring fault | 0.1383 | 0.0374 | 0.0080 | 5.589e-4 | –1.738e-4 |
Rolling element fault | 0.1200 | 0.0287 | 0.0051 | 4.135e-4 | –1.897e-4 |
In order to prove that it is feasible to extract the fault feature of rolling bearing by using CELMDAN and fuzzy entropy, 35 samples are selected for each types of rolling bearing, and their fuzzy entropy is calculated. The boxplots obtained from different samples of each type of rolling bearing are analyzed. The obtained boxplots of each type of rolling bearing are shown in Fig. 9 (a-d), respectively. For each type of rolling bearing, it can be seen from the Fig. 9(a-d) that the fault feature values extracted by CELMDAN and fuzzy entropy have better robustness, and the fluctuation of their feature values is small, which is completely acceptable.
Fig. 9The boxplots of fuzzy entropy of the first five PF components: a) regular, b) outer ring fault, c) inner ring fault, d) rolling element fault
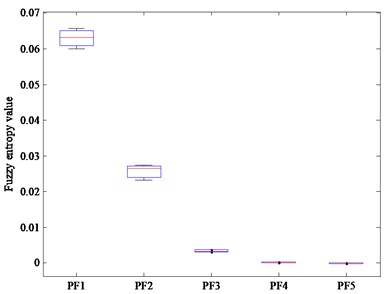
a)
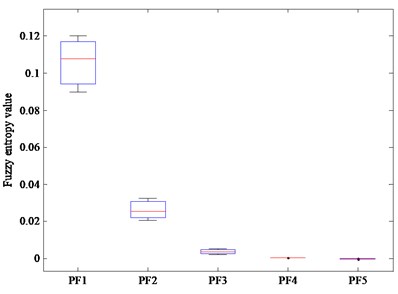
b)
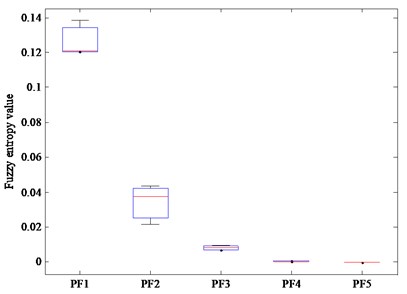
c)
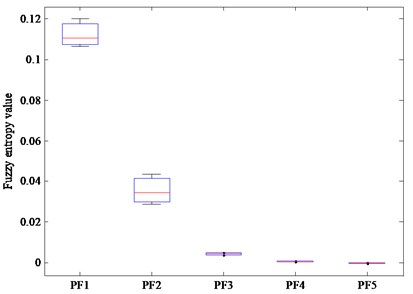
d)
Furthermore, the pattern recognition of rolling bearing is realized by ELM. The number of hidden neurons in ELM is set to 20, and the labels of the training samples of different rolling bearing types are set to λ1, λ2, λ3, λ4, respectively. When the training process is completed, the recognition rate of training samples is shown in Table 3. It can be seen that the recognition rate of training samples is 100 %. Then, the last 25 groups of samples of each rolling bearing state are used for the accuracy testing of the trained ELM, and the diagnosis result of testing samples is shown in Table 4.
Table 3The recognition rate of the training samples of each rolling bearing state
Rolling bearing state | Regular | Outer ring fault | Inner ring fault | Rolling element fault | Recognition rate |
Regular | 35 | 0 | 0 | 0 | 100 % |
Outer ring fault | 0 | 35 | 0 | 0 | 100 % |
Inner ring fault | 0 | 0 | 35 | 0 | 100 % |
Rolling element fault | 0 | 0 | 0 | 35 | 100 % |
From Table 4, the recognition rates of regular and inner ring fault are both 100 %, while those of outer ring fault and rolling element fault are 92 % and 96 %, respectively. The recognition error results are limited to outer ring fault and rolling element fault. It can be seen from Fig. 9 that there are some overlaps between PF1 and PF2 positions of outer ring fault and rolling element fault. This may be due to sporadic similar samples generated by signal interference, and it finally leads to the misdiagnosis of ELM. But in general, fuzzy entropy features effectively distinguish different fault patterns. The overall recognition rate of the proposed method is 97 %, and no fault samples are misdiagnosed as regular state. This means the situation that fault bearing is missed and continues to work can be avoided as much as possible. In order to further analyze the conclusions and prove the effectiveness of the proposed method, some experimental studies under different experiment conditions are carried out. The motor speed is set to 30 Hz and 20 Hz, respectively, and the system load is set to 2.5 Nm and 5 Nm, respectively. The vibration signals of various rolling bearings under different speeds and different loads are collected, and processed according to the above methods. The fault recognition results under different speeds and different loads are shown in Fig. 10.
Table 4The diagnosis result of the testing samples by the trained ELM
Rolling bearing state | Regular | Outer ring fault | Inner ring fault | Rolling element fault | Recognition rate |
Regular | 25 | 0 | 0 | 0 | 100 % |
Outer ring fault | 0 | 23 | 0 | 2 | 92 % |
Inner ring fault | 0 | 0 | 25 | 0 | 100 % |
Rolling element fault | 0 | 1 | 0 | 24 | 96 % |
Fig. 10The fault recognition results under different speeds and different loads
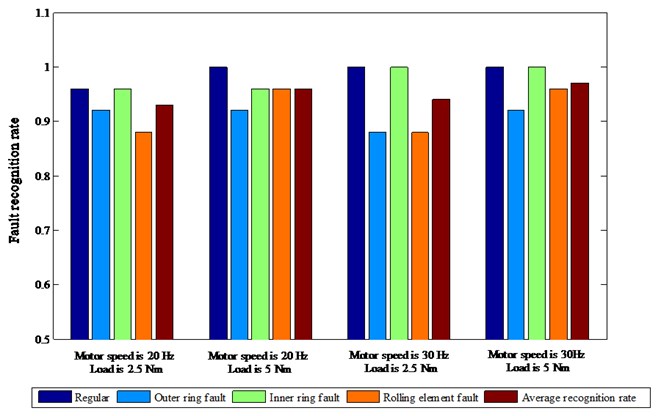
It can be seen from Fig. 10 that when the motor speed is 30 Hz and the load is 5 Nm, the average recognition rate of rolling bearing fault is the highest, reaching 97 %; when the motor speed is 20 Hz and the load is 2.5 Nm, the average recognition rate of rolling bearing fault is the lowest, reaching 93 %. Through comparison, it can also be found that the larger the load is, the higher the recognition rate is. The main reason is that the larger load makes the impact feature signal produced by rolling bearing faults more obvious, and the fault features are easier to be recognized. Through the above analysis, it can be proved that the proposed method has better fault diagnosis results of rolling bearing under constant speed and constant load. That can be applied to the fault diagnosis of rolling bearing under constant speed conditions, so as to avoid safety accidents, and the operation efficiency of equipment can also be improved. But in the actual working condition, there are also a lot of conditions with variable speed and variable load. For the fault diagnosis of rolling bearing under the condition of variable speed, the effectiveness of the proposed method in this paper needs to be further studied, which will also be the main research directions in the future. In addition, how to realize the real-time predictive maintenance of the operation state of rolling bearing is also the research focus of the next step.
5. Conclusions
This paper introduces a bearing fault pattern recognition method based on CELMDAN and fuzzy entropy. By describing the phenomenon of modal aliasing in LMD and combining the previous research, the CELMDAN algorithm is proposed. With the help of noise in different decomposition stages, the modal aliasing problem can be better improved. Further from the perspective of pattern recognition, the fuzzy entropy is defined as the sensitive feature of the rolling bearing vibration signal. It is combined with the simplicity and comprehensiveness of the algorithm. Then the fault diagnosis and pattern recognition of rolling bearing are realized by ELM algorithm. Finally, based on the experiments, it is proved that CELMDAN has better decomposition ability, and fuzzy entropy is an effective and robust feature quantification index. The diagnostic recognition rate of the four types of rolling bearing states is over 92 %, and it is proved that the proposed method can effectively recognize the fault pattern of rolling bearing.
References
-
Kostrzewski M., Melnik R. Numerical dynamics study of a rail vehicle with differential gears. Procedia Engineering, Vol. 192, 2017, p. 439-444.
-
Lu S. L., He Q. B., Wang J. A review of stochastic resonance in rotating machine fault detection. Mechanical Systems and Signal Processing, Vol. 116, 2019, p. 230-260.
-
Wang F. T., Chen X. T., Dun B. S., Wang B., Yan D. W., Zhu H. Rolling bearing reliability assessment via kernel principal component analysis and Weibull proportional hazard model. Shock and Vibration, Vol. 2017, 2017, p. 6184190.
-
Grzegorz K., Li Z. X., Daviu A., Alfonso J. Fault diagnosis of rotating machine. Applied Sciences, Vol. 10, Issue 6, 2020, p. 1961.
-
Yan Z. Y., Hou B. Y., Zhang J. C., Shen C., Shi Y. B., Tang J., Cao Liu H. L. J. MEMS accelerometer calibration denoising method for Hopkinson bar system based on LMD-SE-TFPF. IEEE Access, Vol. 7, 2019, p. 113901-113915.
-
Wang H. J., Fu Y. Study of polynomial fitting technique for EMD end effect. Mechinery Design and Manufacture, Vol. 10, 2010, p. 197-199.
-
Xu L. B., Song Y. Q., Liu Y. Restraining method for end effect based on mirror extension and window function. Computer Engineering, Vol. 41, Issue 4, 2015, p. 112-116.
-
Bouhalais M. L., Djebala A. CEEMDAN and OWMRA as a hybrid method for rolling bearing fault diagnosis under variable speed. The International Journal of Advanced Manufacturing Technology, Vol. 94, Issue 5, 2018, p. 2475-2489.
-
Vanraj, Dhami S. S., Pabla B. S. Non-contact incipient fault diagnosis method of fixed-axis gearbox based on CEEMDAN. Royal Society Open Science, Vol. 4, Issue 8, 2017, p. 170616.
-
Wang Z. J., Wang J. Y., Cai W., Zhou J., Du W. H., Wang J. T., He G. F., He H. H. Application of an improved ensemble local mean decomposition method for gearbox composite fault diagnosis. Complexity, Vol. 2019, 2019, p. 1564243.
-
Zheng J. D., Jiang Z. W., Pan H. Y. Sigmoid-based refined composite multiscale fuzzy entropy and t-SNE based fault diagnosis approach for rolling bearing. Measurement, Vol. 129, 2018, p. 332-342.
-
Chen X., Cheng G., Li Y., Peng L. Fault diagnosis of planetary gear based on entropy feature fusion of DTCWT and OKFDA. Journal of Vibration and Control, Vol. 24, Issue 21, 2018, p. 5044-5061.
-
Baniardalani S., Askari J. Fault diagnosis of timed discrete event systems using Dioid Algebra. International Journal of Control, Automation and Systems, Vol. 11, Issue 6, 2013, p. 1095-1105.
-
Udmale S. S., Singh S. K. Application of spectral kurtosis and improved extreme learning machine for bearing fault classification. IEEE Transactions on Instrumentation and Measurement, Vol. 68, Issue 11, 2019, p. 4222-4233.
-
Hamadache M., Lee D., Mucchi E. Vibration-based bearing fault detection and diagnosis via image recognition technique under constant and variable speed conditions. Applied Sciences-Basel, Vol. 8, Issue 8, 2018, p. 1392.
-
Chen Z. Y., Gryllias K., Li W. H. Mechanical fault diagnosis using convolutional neural networks and extreme learning machine. Mechanical Systems and Signal Processing, Vol. 133, 2019, p. 106272.
-
Wang L., Liu Z. W., Miao Q., Zhang X. Complete ensemble local mean decomposition with adaptive noise and its application to fault diagnosis for rolling bearings. Mechanical Systems and Signal Processing, Vol. 106, 2018, p. 24-39.
-
Zair M., Rahmoune C., Benazzouz D. Multi-fault diagnosis of rolling bearing using fuzzy entropy of empirical mode decomposition, principal component analysis, and SOM neural network, Proceedings of the Institution of Mechanical Engineers Part C, Vol. 233, Issue 9, 2019, p. 3317-3328.
About this article
This work was partly supported by the Special project of science and technology innovation of Tiandi Science and Technology (Grant No. 2018-TD-MS033).

