Phasor measuring unit calibration considering topology expansion of electric power utilities

1.1. Calibration of PMU with topology expansion

The state estimation of power system provides approximate computation for all metered and unmetered quantities. The main intend of SE is to sort out errors due to model approximations and measurement inaccuracies. A state estimator is designed to process the real time meter readings, to handle all the uncertainties and to produce a real time reliable database in order to view the system status. The perspectives of power system SE can be categorized as instrumentation based and tool-based. These perceptions are endorsed to establish a reliable and comprehensive real-time database [1]. Conferring to the assessment of SE, the following aspects will be the future trend.

• Wide-area power system by formation of multiple zones with interconnection between each network.

• Real-time SE algorithm using time stamped GPS Technology.

• Finally, the expansion of topology to get complete observability.

PMU is a device used to monitor the state of power systems and control applications. So it is the inevitable tool in smart grids. The PMU data is highly accurate but their measurements are not effectuated sometimes due to various abnormal conditions arise in the system. The data quality issues experienced by PMUs can be addressed by calibration. PMU calibration schemes can be performed as offline testing and using mathematical models.

The offline testing/calibration method entails expert equipment/system and also instrumentation channel errors cannot be replicated. The mathematical model checks the loyalty of the system. The influence of the exactitude of PMU devices focuses on algorithms proposed the estimation of dynamic Phasor, and interpretations their enactments under various conditions [2]. The impacts of these sources are summarized into: random and bias error. Random errors are arithmetical vacillations of the measurements because of the meticulous limitations of the PMU device that is avoided by measuring through statistical mean. The bias error is reproducible inaccuracy and is consistent. It is difficult to estimate and analyzed statistically. Calibration of multiple PMU is integrated into higher-level topologies for effective measurements. The complexities of these topologies vary from full network systems over a geographical area.

1.2. Research hiatus

Calibration of PMU devices and estimating the conditions of the system are the major concerns in modern power systems. As mentioned formerly, a large system to monitor will be the potential advancement to explore the SE process, precise calibration of these PMU devices is required. Also, the potential concert of PMU will be mislaid due to the existence of biased error. Therefore, it is apparent that accuracy should be assured for the performance of smart grid. Taking the aforementioned concern, an optimal approach with the objective to ensure maximum accuracy of the network is unified with PMU placement problem.

1.3. State-of-the art work

The bias error occurred while calibrating the PMUs and extending the topology of different test systems is considered as the major pressing problems in SE. A recent survey on the problem of calibrating the PMUs precisely with bias error embraces a widespread procedure to obtain the phasor representation of an input signal and applying discrete transform to compute the consequent Phasor [3]. The synchrophasor based calibration framework has been developed considering overall bias error [4]. However, it depends on a particular model for measuring the synchrophasors that is implemented in a PMU. Perhaps, a comprehensive study on finding the appropriate PMU locations to ensure minimum estimation error and the correctness of it [5]. The estimation process for the intention of minimizing the impact of measurement error [6]. The foremost drawback is that a two terminal transmission line model is utilized. An augmented method for voltage transformers calibration using synchrophasor measurement of ratio and bias errors is recommended [7]. The PMU calibrations are stipulated for enhancing the correctness of PMU measurements [8]. But due to less accuracy, it may be complicated to implement the PMUs across a wide area network. An algorithm has been developed to calculate calibration factors (CFs) using a measuring model [9]. Conversely, it is observed that the level of calibrations is increased. With the aforementioned difficulties that crafts traceable magnitude and phase calibration for ac signals, active and passive components and extend the automatic finding and correcting the bias error have been analysed [10-12]. Despite the facts, the models detailed provide an iterative based elucidation. The latter work integrates synchronized measurement calibration process causing several distinct sources of errors [13]. The calibration of the measurement problem and secondary of it are detailed [14, 15]. Nevertheless, implementation and performance details are not endowed.

In correlation with the above model, an instrument transformer for calibration of ratio and factors of phase angle has been propounded [16]. But this method is used for multiple sets of measurements. It is detailed for calibrating the PMUs [17], but it requires multiple data for reducing the error. The algorithm of fault location is entrenched to investigate the PMU response error [18]. Nevertheless, the technique has integrated the calibration of error by placing the PMUs. Testing the function of PMUs and observation of their consistent accuracy have been demarcated [19]. However, such estimation produces a mismatch between the measured phasor and the actual phasor. The parameter error identification method detects and identifies measurement errors by placing the PMUs at appropriate locations [20]. Conversely, the tactic does not contemplate the assessment of large scale systems. An approach for PMU placement considering both existence and lack of conventional measurement is presented [21]. In addition, a methodology for estimating the uncertainties based on the WLS state estimation related to the PMU measurements are promulgated [22]. Yet, the approach contemplates those measurements which are not free from errors. An approach combines the analysis of observation and detection of bad data into a single framework to solve PMU placement problem for SE [23]. It is observed that these algorithms have not focused on calibration of PMUs. An on line error correction method to precise both the resonance error and saturation error is suggested [24]. Moreover Using PMUs the linear estimation is presented and the transmission of line parameter is identified [25]. Furthermore, microprocessor based phasor measurements [26], with necessary cradles of information for predicting the instability of the system and perceiving the uncertainties in analog measurements is indorsed [27]. In all the circumstances that has been enumerated in the chronological order, PMU calibration has not been taken in the interpretation. Even though testing and calibrating the PMUs with the TESLA 3000 DRF using Doble F6150 has been assimilated [28], only a multi time framed recording system is used for monitoring electric power systems. A MICA based algorithm is suggested [30] for OPP in case of normal and abnormal conditions. According to the above details, the concept of deploying PMUs considering topology expansion, calibration of PMUs with bias error is mislaid in the above literatures. Hence, this article highlights a significant interest in extending the topology of the network and calibrating the PMUs accurately with consideration of bias error.

1.4. Motivation and objectives

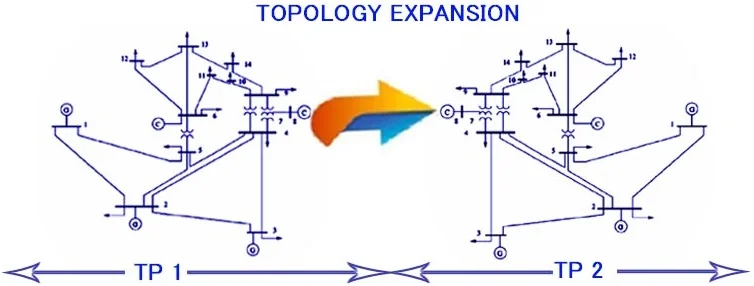
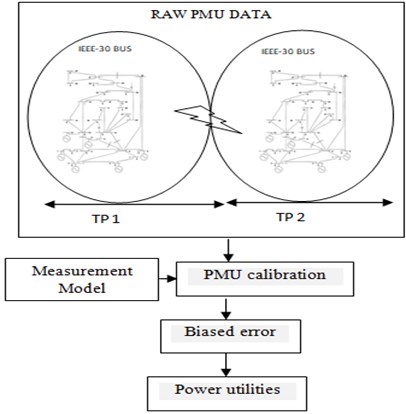
Referring Table 1, there has been significant reports detail the PMU calibration and finding the bias error. The bias error will be exposed only when there is delay from the output of transducer to the input of PMU device. For efficient monitoring and various control applications PMU device can be used in which the bias error is incorporated to correct the PMU data. The primary focus is on the issue of topology extension based on the set of performance evaluation metrics. To the knowledge of authors, there is no previous study (Table 1) on this subject extending the topology of test systems, calibrating the PMU device and identifying the bias error (in a single framework). The proposed methodology is clearly deliberated in Fig. 1.

1.5. Article organization

This paper is arranged as follows. Section 2, establishes a mathematical model to incorporate their objectives. In Section 3, the algorithm for solving the proposed model using WOA is conferred. In Section 4, the topology extension for different test systems and normalized error measurement considering various scenarios has been conferred. Finally, in Section 5 conclusion of the paper and future work has been presented.

Fig. 1Proposed calibration of PMU for topology expansion

2.1. Formulation of normalized PMU error

True value of error is considered as the decisive factor for the purpose of estimating PMU measurements. The value of error is a gauge between true value and measured value which is represented in terms of magnitude. When the amount of error is minimized the utmost efficiency of the SE is guaranteed. The accuracy of estimation is calculated as:

For the purpose of formulating the actual level of error [5], is espoused because it considers enhancing the accuracy of estimation as one of the major rationale for deploying the PMUs where, $N$ is the number of PMUs that are to be in position in the power system of $n$ buses ($N<n$).

2.2. Observability-constrained PMU

The intention of extending the topology of the network buses is to discover the rigid structure that fits into the province. For the class of over changing, complex, and common world problems, the fundamental subject discriminating countervail nature of our prevailing the current search algorithms could be counterproductive to growing explorative behaviour. In addition, it should satisfy the boundary constraints and it should have prescribed number of PMUs. After topology extension, the dilemma becomes:

The optimization problem that minimizes the objective function given in Eq. (2) should satisfy the constraint Eq. (3). Therefore, as a result of placing less quantity of PMUs while extending the topology of PMUs, the value of error will reach a minimum value which in turn leads to maximum efficiency.

3.1. Necessity of optimal tool

The foremost intend of the projected technique of topology expansion is to compute the minimum locations and coverage of PMUs that ensure complete observation of the system. This kind of natural extension facilitates to extort the most significant locations which in turn enhance the decision-making process. Thus, it is apparent that the process of topology expansion provides more valuable information for which a minimum optimal location of PMU is required. Concurrently, for handling the non-linear constraint in the projected model an efficient algorithm must be explored in an efficient way. Therefore, the optimal locations of PMU are determined using whale optimization algorithm.

Fig. 2PMU placement using WOA for topology expansion

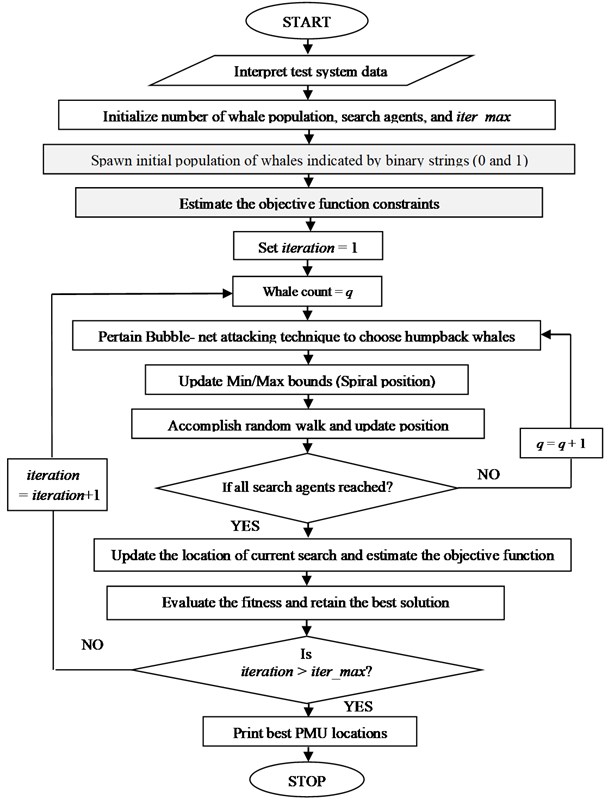
The reason behind choosing this swarm-based technique is that most of the mathematical models are just a generalization of the real problem and it does not embrace the entire facets of the proposed problem whereas, whale optimization algorithm (WOA) is able to decipher the optimization problems with curtailing the hunting behaviour of humpback whales. Furthermore, WOA leads to rapid discovery of good solutions [29]. Therefore, instead of mathematical models it is necessary that a swarm based meta-heuristic technique is essential for solving the process of topology expansion. The flow chart of computation of WOA is detailed in Fig. 2.

3.2. Calibration and normalized error

For the intention of ensuring accuracy in PMU, conventional measurements are employed. Calibration is considered as one of the significant factors for the reason of generating highly accurate measurements. The consequent PMUs must be calibrated with the aid of CFs. Unanimously, two varieties (rectangular and polar coordinates) of formulations and two methods (online and offline) are used to estimate the corresponding CFs. In this paper, the CFs evaluated using the polar coordinates in offline mode.

There are numerous categories of optimization procedure for estimating the bias error in the precise quantity. In the proposed model the actual error is calculated using Eq. (1) where, the disparity between the value got by measuring and that of actual is alienated by multiplying with the $n$ number of network buses ($n$×2). In addition, the biased error (20 % and 50 %) is introduced in the impedances of the corresponding data (Power Systems Test Case Archive – UWEE), for different test systems. By using the real PMU data, the bias errors in the measured phasors can be estimated in offline mode. Moreover, the approach of estimating the bias error does not entail any sort of parameter but, the presence of unbiased arbitrary noise from instrumentation channel the potential performance in the actual field installation cannot be achieved.

4.1. Optimizing PMU locations with topology extension for different test systems

This section discovers and crams about extending the topology of different test systems. In reality this is identified as left undone of topologies that are defined. During topology extension it is necessary to consider the aspects such as size and formation of the network, selection of optimal locations, and cost saving. The model of topology extension for the corresponding network is the most vital concern in placement of PMUs. The concept of topology extension can be formed by probabilistic method where each bus randomly designated a binary number (1 or 0). For example, in Table 2 consider the case of IEEE-14, IEEE-30, IEEE-57 and IEEE-118 bus systems where in normal operation without consideration of topology extension 4, 10, 17, 32 PMUs are desired to ascertain full observation of the network. But when the same test systems are extended naturally ($n$×2) then a minimum of 7, 20, 33, 64 PMUs is placed at corresponding buses which does not ensure full system observability. In addition, the coverage provided by the corresponding PMUs will also be large. Therefore, if the network is extended because of increasing patrons then such PMU devices are needed to be calibrated.

4.2. Calibration analysis

4.2.1. Normalized error measurement

Calibration is the way to determine the correct value of the PMU device by comparing the known value of measurements with the value that needs to be calibrated. The method is followed to ensure that the measurements within the IEEE standards. During the first phase of calibration of PMUs, each PMU is placed in the corresponding locations thus compromising the amplitude and phase angle of the measured phasors. The following three scenarios are conversed to exhibit the applicability of the intended PMU data calibration framework.

4.2.1.1. Scenario 1: using authentic PMU data

The ameliorated eventuality as delineated in Tables 3 and 4 consists of voltage (Magnitude), angle (Degree) and aggregate vector erroneousness for IEEE-14 and IEEE-30 bus systems. In this scenario, the bias error is not incorporated in the impedance references, i.e., only real PMU data are integrated. The magnitude measurement error in this scenario is much lesser when compared to other two scenarios. It can be seen from the Tables 3 and 4 and from the corresponding Fig. 3 and 4 that the true bias error reaches zero for some of the buses in both the test systems. For example, the IEEE-14 bus system (Table 3) shows that the magnitude difference in 2, 3, 6 and 8 will be zero. The true errors are within the limit. Therefore, by using PMU data it is clear that the buses will not become much sensitive and the erroneousness of the instrumentation channels can be corrected at this phase.

Table 3Bias error identification for IEEE-14 bus system

Bus No.	Voltage (Mag.)	Angle (Deg.)	Error
1	1.031	0.000	1.036×10-3
2	1.045	–4.986	0
3	1.010	–12.729	0
4	0.971	–9.895	1.4×10-5
5	0.982	–8.183	6.5×10-6
6	1.070	–14.221	0
7	0.995	–14.631	4.6×10-6
8	1.090	–13.361	0
9	0.970	–17.180	1.02×10-5
10	0.968	–17.542	6.6×10-6
11	0.988	–17.298	1.2×10-5
12	0.996	–18.001	1.3×10-5
13	0.986	–18.059	1.35×10-5
14	0.950	–19.026	1.1×10-5

Fig. 3Comparison of bias error for IEEE-14 bus system

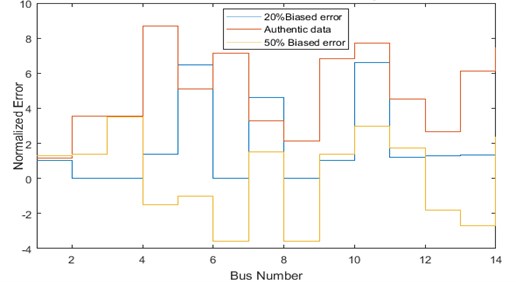
Fig. 4Comparison of bias error for IEEE-30 bus system

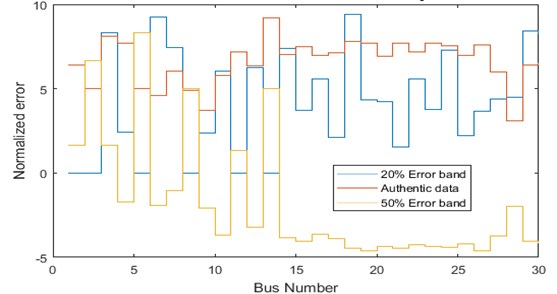
Table 4Bias error identification for IEEE-30 bus system

Bus No.	Voltage (Mag.)	Angle (Deg.)	Error
1	1.060	0.0000	0
2	1.043	–5.487	0
3	1.022	–8.004	8.3×10-6
4	1.013	–9.661	2.4×10-6
5	1.010	–14.371	0
6	1.012	–11.398	9.23×10-7
7	1.003	–13.150	7.45×10-6
8	1.010	–12.100	0
9	1.051	–14.384	0
10	1.044	–16.024	6.02×10-6
11	1.082	–14.394	0
12	1.057	–15.242	0
13	1.071	–15.242	0
14	1.042	–16.131	0
15	1.038	–16.228	0
16	1.045	–15.830	0
17	1.039	–16.188	2.13×10-6
18	1.028	–16.824	0
19	1.025	–17.052	4.36×10-6
20	1.029	–16.852	4.24×10-6
21	1.032	–16.468	1.52×10-6
22	1.033	–16.415	0
23	1.027	–16.612	0
24	1.022	–16.830	7.3×10-6
25	1.019	–16.424	2.2×10-6
26	1.001	–16.842	3.64×10-6
27	1.026	–15.912	4.4×10-6
28	1.011	–12.057	4.5×10-6
29	1.006	–17.136	8.4×10-7
30	0.995	–18.015	8.2×10-6

4.2.1.2. Scenario 2: 20 % error band

In this scenario an error of 20 % is incorporated for impedances in the corresponding data and the results given in Tables 5 and 6. It can be perceived from Tables 5 and 6 and Figs. 3 and 4 that none of the buses in both the test systems (IEEE-14 and IEEE-30 bus systems) has zero as actual error. This procedure indicates that the calibration can also be done remotely at phasor data concentrator. The intent of establishing random errors is not only to resolve which bus is more accurate, but moderately detect and establish the incongruity so that improvements can be done while calibrating the PMUs in corresponding locations.

Fig. 5Error band accumulation for IEEE-14 bus system (bus vs voltage magnitude)

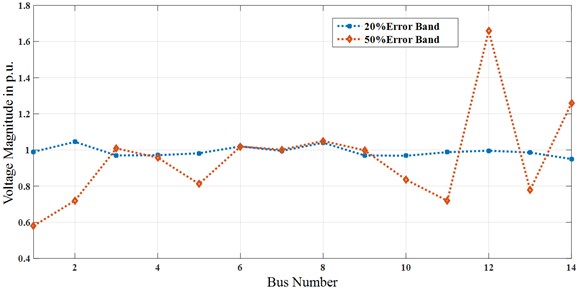
Fig. 6Error band accumulation for IEEE-14 bus system (bus vs error)

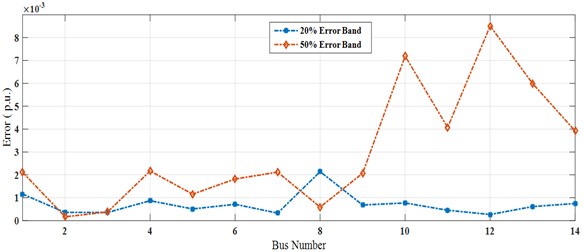
Table 5Error band accumulation for IEEE-14 bus system

20 % error band				50 % error band
Bus No.	Voltage (Mag.)	Angle (Deg.)	Error	Voltage (Mag.)	Angle (Deg.)	Error
1	0.99	0.000	1.16×10-3	0.58	0.000	2.11×10-3
2	1.045	–4.064	3.57×10-4	0.72	–27.13	1.67×10-4
3	0.970	–20.920	3.57×10-4	1.009	–17.03	3.79×10-4
4	0.971	–17.628	8.69×10-4	0.958	–29.91	2.17×10-3
5	0.982	–11.117	5.1×10-4	0.812	–22.17	1.157×10-3
6	1.020	–18.773	7.14×10-4	1.019	–16.115	1.82×10-3
7	0.995	–19.816	3.28×10-4	1.002	–21.47	2.12×10-3
8	1.040	–19.816	2.14×10-3	1.050	–26.14	5.91×10-4
9	0.970	–22.044	6.82×10-4	0.998	–12.580	2.07×10-3
10	0.968	–22.344	7.72×10-4	0.836	–13.991	7.19×10-3
11	0.988	–20.865	4.52×10-4	0.719	–26.781	4.07×10-3
12	0.996	–21.021	2.67×10-4	1.659	–21.128	8.51×10-3
13	0.986	–22.102	6.13×10-4	0.778	–18.55	5.99×10-3
14	0.950	–24.059	7.49×10-4	1.259	–19.37	3.92×10-3

4.2.1.3. Scenario 3: 50 % error band

In this scenario, the intended model is tested by dealing with big magnitude error. Here, an error of 50 % is added in the corresponding bus impedances and the results given in Tables 5 and 6 and in Figs. 3 and 4 respectively. From Table 5 it is found that the worst case situation occurs when an error of 50 % added to each impedance in the corresponding data and the true bias error will never get minimized to zero. Also, for some of the corresponding buses (in IEEE-14 and IEEE-30 bus) the true error remains negative which in turn indicates that the calibration aspects remain inaccurate. Therefore, when the PMUs are calibrated with large magnitude errors then it will be very difficult to realize the accuracy of such devices. Figs. 5 to 8 shows that the error band accumulation for IEEE-14 and IEEE-30 bus system.

Table 6Error band accumulation for IEEE-30 bus system

20 % error band				50 % error band
Bus No.	Voltage (Mag.)	Angle (Deg.)	Error	Voltage (Mag.)	Angle (Deg.)	Error
1	0.996	0.000	6.4×10-2	0.91	0.000	2.91×10-4
2	0.993	–24.866	5×10-1	0.996	–16.8	9.01×10-4
3	0.940	–18.817	8.1×10-2	1.036	–23.7	4.67×10-4
4	0.935	–31.527	7.7×10-2	0.905	–34.57	8.93×10-3
5	0.960	–46.761	5×10-1	0.911	–27.03	7.88×10-4
6	0.966	–39.828	4.6×10-2	1.278	–37.18	6.54×10-3
7	0.943	–45.124	6.04×10-2	0.917	–41.29	3.03×10-3
8	1.010	–43.914	4.9×10-2	1.1894	–28.02	6.78×10-4
9	1.014	–44.505	3.7×10-2	1.0916	–33.047	7.16×10-3
10	0.986	–48.062	5.8×10-2	1.002	–45.9	1.53×10-3
11	1.082	–44.505	7.2×10-2	0.958	–43.18	4.42×10-3
12	0.994	–44.649	6.33×10-2	1.0018	–52.30	3.18×10-4
13	1.071	–44.649	9.2×10-1	0.993	–50.93	4.86×10-4
14	0.972	–47.182	7.04×10-2	0.987	–54.09	2.15×10-3
15	0.963	–48.044	7.47×10-2	1.015	–56.71	7.92×10-4
16	0.975	–46.875	6.96×10-2	1.029	–50.06	5.17×10-4
17	0.968	–48.394	7.11×10-2	1.36	–46.037	3.17×10-4
18	0.950	–49.836	7.79×10-2	0.983	–59.178	3.84×10-3
19	0.948	–50.646	7.72×10-2	0.937	–58.27	2.53×10-4
20	0.960	–49.767	6.92×10-2	0.9916	–63.89	1.99×10-3
21	0.955	–50.158	7.70×10-2	1.40	–59.11	3.87×10-3
22	0.961	–49.636	7.16×10-2	1.005	–76.78	1.12×10-3
23	0.950	–49.574	7.72×10-2	0.994	–68.93	5.66×10-3
24	0.946	–50.556	7.55×10-2	1.38	–62.37	7.81×10-4
25	0.949	–50.278	6.98×10-2	1.016	–70.27	7.53×10-4
26	0.925	–51.220	7.62×10-2	0.923	–57.3	6.07×10-3
27	0.966	–49.320	5.97×10-2	0.856	–65.06	4.18×10-3
28	0.980	–43.082	3.07×10-2	0.917	–71.915	3.11×10-3
29	0.942	–51.367	6.39×10-2	0.930	–76.81	8.013×10-3
30	0.929	–52.736	6.55×10-2	0.962	–58.016	6.14×10-3

Fig. 7Error band accumulation for IEEE-30 bus system (bus vs voltage magnitude)

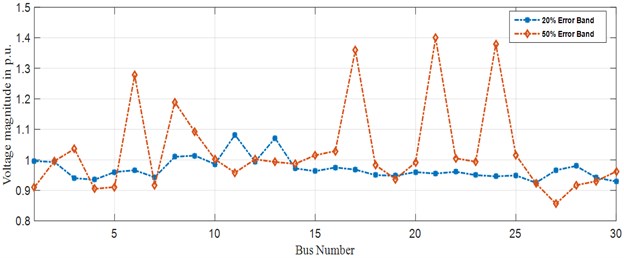
Fig. 8Error band accumulation for IEEE-30 bus system (bus vs error)

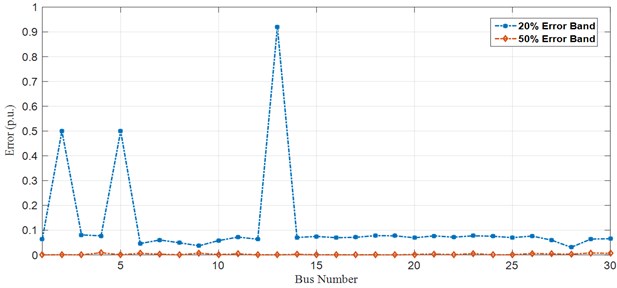
Table 7Comparison of optimal PMU placement between normal condition and topology extension

Test system	Coverage
	Normal operating condition		Topology extension
	WOA	Ref. [30] MICA	WOA
IEEE-14 Bus	19	17	37
IEEE-30 Bus	52	48	104
IEEE-57 Bus	69	67	139
IEEE-118 Bus	163	162	332