PCA based health indicator for remaining useful life prediction of wind turbine gearbox

1. Introduction

In recent years, harnessing of wind through off-shore wind turbines has increased significantly. However, wind energy industries are experiencing longer downtimes, high maintenance costs and less reliability. As the wind energy industries are located in remote and unmanned regions, it is very difficult to implement reactive and preventive maintenance strategies. In order to make wind energy competitive and economically viable, condition based maintenance is being employed, which allows the scheduling of maintenance thereby reducing the unexpected downtimes [1]. Condition monitoring (CM) systems consists of two sub-systems, namely, fault diagnosis and fault prognosis. Fault diagnosis is defined as detection of physical fault in a mechanical system and classification of the fault type whereas fault prognosis is concerned about predicting the remaining useful life (RUL) of the mechanical system [2]. Previous researchers have used vibration analysis in order to diagnose the defect present in the wind turbine gearbox and further quantified the severity level using various machine learning algorithms [3, 4]. As the acquired vibration signatures are noisy and have non-linear nature, recent studies are more concerned about the implementation of various signal processing algorithms such as wavelet transform, empirical mode decomposition to extract the fault sensitive information from the acquired data [3, 5].

On the other hand, the research investigations related to the RUL prediction of wind turbine gearbox are limited, because of the complexity of gearbox, acute changes in the operating conditions and non-linear nature of the acquired vibration signals [6]. Besides that, prediction of RUL mainly depends on the assumption that mechanical component failure is preceded by a period where there is extent of deviation or smooth degradation of the system from its expected normal operating condition. This can be done using two approaches: model based approach and data-driven approach. Prediction of RUL through model based approach uses finite element models to examine the overall stress distribution so as to predict the RUL according to damage propagation mechanism. However, this approach is far from reality as it consists of many assumptions and also it is quite challenging to model the complex gearbox and non-linearities that arises due to the changes in loading [6]. On the other hand, data-driven approach detects the degradation and predicts the RUL of the mechanical components based on the available run-to-failure data. Usually, in data-driven approach, a cumulative health indicator (HI) is modelled in order to indicate the degradation of the mechanical components and then this HI values are used to correlate the acquired data so as to predict the RUL of the component [7]. Majority of the previous research investigations have predicted the RUL of the components of electrical and mechanical systems while the operating conditions are stationary. However, there exists a dearth of literature about the prediction of RUL of wind turbine gearbox as it is a complex system subjected to non-stationary loads. This investigation models an exponential degradation model in order to predict the RUL of the wind turbine gearbox subjected to non-stationary operating conditions.

2. Experimental details

2.1. Experimental test-rig

A customized miniature wind turbine planetary gearbox was designed and constructed with an overall gear ratio of 1:100, refer Fig. 1. The gearbox consists of three stages, two planetary and one parallel stage. The gearbox was in perfect working order at the start of the experiment. All components of the gearbox were free from defects. The experiment was run for a total of 345 hours. The experiment was stopped when the gearbox failed catastrophically. The system was automated to acquire data. Accelerometers were stud mounted at appropriate points. The sample rate was set at 12 kHz. The sensors are connected to data acquisition device and further to the computer.

Fig. 1Experimental setup- miniature wind turbine planetary gearbox

2.2. Methodology

The vibration signals are acquired and further processed using continuous wavelet transform (CWT). CWT provides time-frequency representation of the original vibration signal through a mother wavelet [4]. CWT yields to a series of wavelet coefficients having same length as that of the original signal, also expressing similarity between the original signal and mother wavelet function for a given scale. Morlet wavelet was used as the mother wavelet in the present investigation while decomposing the vibration signal CWT. Further, various statistical features are computed from the CWT coefficients. These statistical features are used to construct the health indicator which is further extrapolated to predict the RUL of the wind turbine gearbox, refer Fig. 2.

Fig. 2Experimental methodology

3. Modeling of health indicator

The obtained statistical feature set is a high dimensional data matrix and it consists of noise as well as non-linear variability, which requires large amount of computational power to process. Besides that, the large feature set can lead to smearing effect if not pre-processed and can also cause overfitting. Therefore, it is necessary to pre-process the features dataset to establish an effective health indicator to develop the degradation model. Initially, the obtained feature set is normalized to reduce the data redundancy which further improves the overall integrity of the dataset. Min-max normalization has been used and it maps the entire range of feature set to the range of 0 to 1. Eq. (1) is used to perform the normalization and it is shown below:

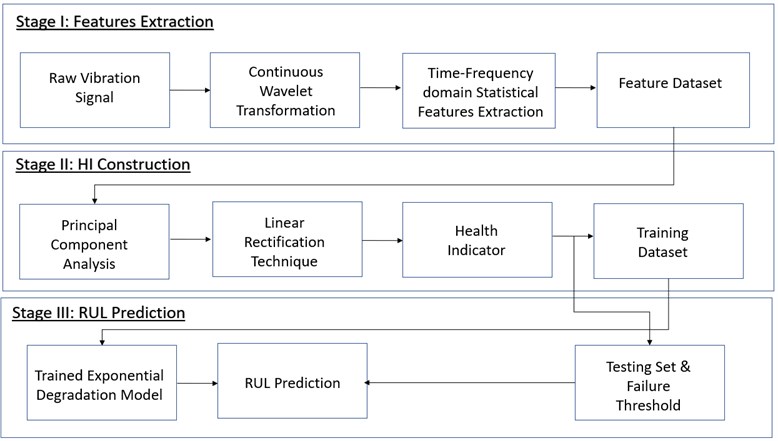
where, $a_i$ is the value of $i$th data, $a_{min}$ is the minimum value of the data and $a_{max}$ is the maximum value of the data. Therefore, the high dimensional feature data set has been normalised and it is subjected to dimensionality reduction in order to reduce the computational time. Principal component analysis (PCA) is an unsupervised machine learning algorithm used for the dimensionality reduction [8]. PCA is a mathematical approach that performs the orthogonal linear transformation on the input data in such a way that, the data consists of greatest variance (principal component 1) comes to as the first coordinate, the next greatest variance (principal component 2) lie as the second coordinate, and so on. The $n$-dimensional feature matrix $X$ consisting of the feature values corresponding to runtime of $n$ (in days) as row vectors and the $d$-dimension feature vectors as column vector is devised and supplied as input matrix to PCA. PCA computes the principal components (eigen vectors) from the input matrix which determines the directions of the new feature space and eigen values which corresponds to their magnitude. PCA computes the principal components (PCs) and the defect sensitive information of the original vibration signal is retained in the initial few PCs. As the first PC (PC1) consists of 90 % of the variability of the original signal, the information pertaining to PC1 has been chosen as the health indicator (HI). Fig. 3 represents the trend of raw and smoothened health indicator for the run time of 292 hours. It can be observed that, rather than exhibiting a regular expected trend, the health indicator gives local variation with the machine run time. It is quite challenging to make any inference about the RUL and hence, the HI trend needs to be smoothened/rectified. Linear rectification technique (LRT) has been applied to smoothen the spurious local fluctuations present in the HI trend in the form of sudden peaks or unexpected valleys [9]. Mathematically, LRT smoothening and growth rate of HI are explained by Eqs. (2) and (3) respectively:

where, $h_i$ indicates the value of HI at run time $t_i$, $\eta$ indicates the growth rate within certain window. Therefore, LRT produces a progressively increasing trend that corresponds to the degradation of the components.

Fig. 3Evolution of health indicator a) raw health indicator b) smoothened health indicator

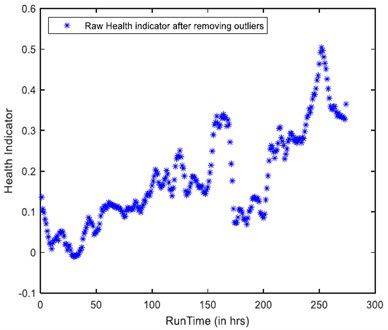
a)

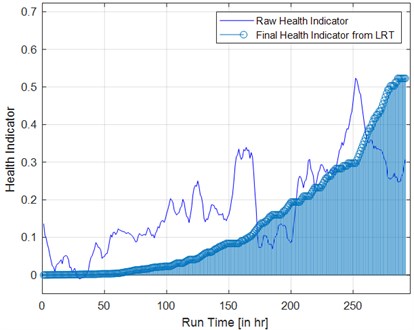
b)

4. Remaining useful life prediction

The LRT smoothened HI trend for the available acquired vibration data is constructed and the prospective values of HI are predicted until the threshold value reaches. Exponential degradation model is used to predict the RUL and is defined by Eq. (4):

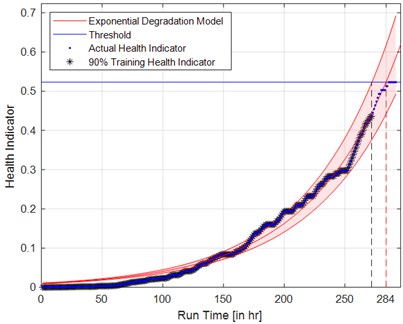
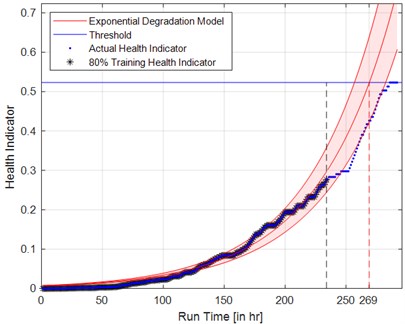
Among the acquired vibration data of 292 hours, 90 % of the data (about 262 hours) is used for constructing the HI thorough exponential fit. The threshold for confidence interval is taken as 0.9, and it signifies that, the predicted exponential fit contains the true population mean as 95 % [10]. Fig. 4(a) illustrates the trend of actual HI, predicted trend of HI through exponential degradation model. It can be observed that, the predicted HI trend through exponential model reaches the threshold value (0.5) at 284 hours which is close the actual run time of 292 hours and the error percentage is 2.73 %. In order to ensure the reliability of the proposed method, another trail of RUL prediction is performed by considering 80 % of the data (about 233 hours) for building the HI through exponential fit. It can be noted that, the HI through exponential model has reached the threshold value at 269 hours and the error percentage is 7.19 %, refer Fig. 4(b). Therefore, the proposed approach is able to predict the RUL of the wind turbine gearbox and it requires considerable amount of historical data for training the exponential model.

Fig. 4Prediction of RUL: a) 90 % training health indicator, b) 80 % training health indicator

5. Conclusions

In this study, a novel health indicator (HI) was constructed in order to predict the remaining useful life of the wind turbine gearbox. Run to fail experiments are performed on a laboratory scaled wind turbine gearbox of overall gear ratio 98:1. Vibration signature were acquired, and continuous wavelet transform was applied to decompose the acquired raw signals. Various statistical features were computed from the wavelet coefficients which form the input feature set. Principal component analysis was performed and principal components (PCs) are computed from the input feature set. PC1 was considered as health indicator and the trend of PC1 was further smoothened by linear rectification technique. Exponential degradation model was fit for the considered health indicator and the model was able to predict the RUL of the gearbox with an error percentage of 2.73 %. Thus, the proposed approach was able to predict the RUL of the wind turbine gearbox which in turn requires considerable amount of historical data for training the exponential model. The scope of the present study includes the establishment of an adaptive failure threshold in order to predict the remaining useful life more precisely.