Study on penetration characteristics of honeycomb aluminum

1. Introduction

Honeycomb aluminum is a good cushioning energy absorption material, which can absorb a lot of energy in the process of dynamic impact, so it is made into a variety of cushioning energy absorption components, which are widely used in military, transportation, packaging, construction and other fields.

The coplanar and heteroplanar mechanical properties of honeycomb materials were analyzed theoretically by Gibson and Ashby [1]. Yu Jiang et al. [2] simulated and studied the coplanar impact mechanical properties of circular honeycomb aluminum. D. Ruan et al. [3] studied the deformation mode and platform stress of honeycomb aluminum under in-plane dynamic compression by finite element analysis. Sun Deqiang et al. [4]. studied the deformation mode, elastic modulus and energy absorption of double-walled thick honeycomb aluminum core under coplanar impact load. Hul L. et al. [5]. studied the in-plane collapse deformation mechanism of honeycomb aluminum under high speed impact by LS-DYNA, and gave the platform stress formula of honeycomb aluminum under dynamic load. Zou Z. et al. [6] studied the platform stress and energy absorption of honeycomb aluminum under coplanar impact load by numerical simulation. The in-plane quasi-static platform stress of honeycomb is analyzed by Qiu X. M. [7] theory, the in-plane dynamic response of honeycomb aluminum is simulated, and the platform stress formula under dynamic load is obtained. T. Wierzbicki et al. [8] studied the compressive mechanical properties of metal honeycomb on different surfaces, and put forward the formula of static collapse stress on different surfaces. M. Yamashita [9] analyzed the out-of-plane compression mechanical behavior of honeycomb aluminum by means of experiment and numerical simulation.

Most of the above studies are about the compressive mechanical properties of honeycomb aluminum, and the penetration of honeycomb aluminum is rarely involved. Therefore, in this paper, the mechanical behavior of projectile penetrating into honeycomb aluminum with different wall thickness is studied by means of numerical simulation and experiment.

2. Simulation and analysis of projectile penetrating honeycomb aluminum

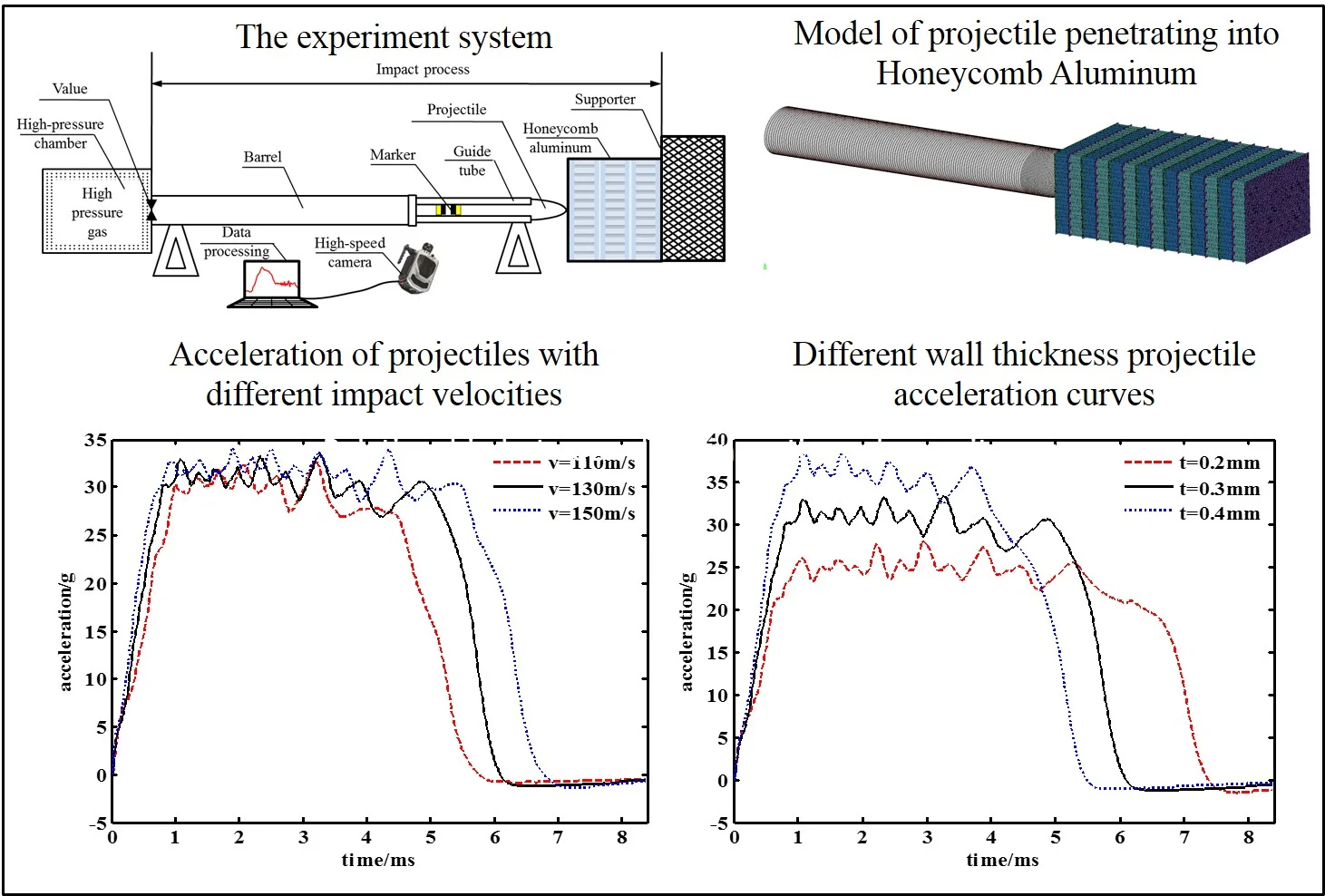
The shell element finite element model of projectile penetrating honeycomb aluminum is established by using LS-DYNA. In order to reduce the calculation scale, according to the symmetry, the model is established, as shown in Fig. 1.

Fig. 1Model of projectile penetrating into honeycomb aluminum

The projectile is a spherical projectile with a warhead radius of 55 mm, a cylinder and a hollow structure. In this paper, ten layers of stacked honeycomb aluminum plate are studied in this paper. The specification of each plate is 200 mm × 200 mm × 50 mm, and the honeycomb aluminum is commercial double-wall thick honeycomb aluminum. The related simulation parameters as shown in Table 1 and Table 2.

3. Experiment of projectile penetrating honeycomb aluminum

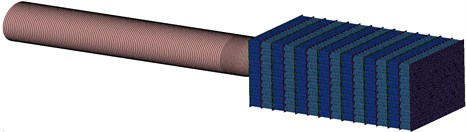
The air gun is used as the power device for the projectile to penetrate the honeycomb aluminum. The experiment system is composed as shown in Fig. 2. The projectile is mounted inside the barrel, close to the high pressure chamber. When launched, the release mechanism opens quickly, the gas pressure is applied to the projectile, and the projectile is accelerated until it flies out of the muzzle. In the process of penetrating into honeycomb aluminum, the local fracture and compression of honeycomb aluminum are caused by projectile. The penetration displacement of projectile is measured by high-speed camera and motion analysis software. The impact acceleration is obtained by quadratic differential operation after data preprocessing.

Fig. 2The experiment system

4. Results and discussion

4.1. Results of simulation and experiment

The deformation of honeycomb aluminum and finite element simulation after the experiment is shown in Fig. 3. It can be seen from Fig. 3 that the projectile penetrates into the honeycomb aluminum mainly due to local shearing and tearing deformation, and the overall structure deformation of the honeycomb aluminum is small. This is because the strength of the experiment honeycomb aluminum is low, and the honeycomb aluminum is first broken and destroyed when it is impact by the projectile, and the overall structure is not subjected to sufficient force to deform it.

Fig. 3Simulation and experimental results

a) Experiment

b) Simulation

4.2. Discussion of simulation and experimental results

(1) Relationship between projectile velocity and acceleration.

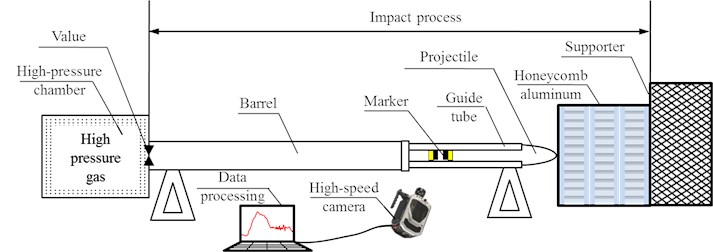
The acceleration curve of the projectile at different velocity is shown in Fig. 4(a), and the peak acceleration and pulse width (acceleration duration) are shown in Table 3. The results show that with the increase of projectile velocity, the initial kinetic energy obtained by projectile increases, the peak acceleration increases, and the pulse width of acceleration increases. In addition, with the increase of projectile velocity, the velocity of projectile acceleration reaching the maximum peak is faster.

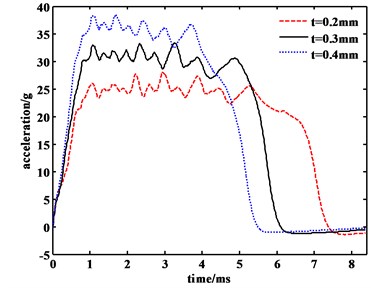
Fig. 4a) Acceleration of projectiles with different impact velocities (t= 0.3 mm), b) different wall thickness projectile acceleration curves (v= 130 m/s)

a)

b)

Table 3Impact acceleration peak and pulse width of projectiles with different impact velocities

Velocity (m/s)	Acceleration peak (g)	Pulse width (ms)
110	3260	5.83
130	3276	6.18
150	3387	6.96

5. Relationship between wall thickness and acceleration

The acceleration curve of the projectile at different wall thickness is shown in Fig. 4(b), and the peak acceleration and pulse width (acceleration duration) are shown in Table 4. The results show that with the increase of wall thickness, the relative stiffness of honeycomb aluminum increases, the peak acceleration increases, and the acceleration pulse width decreases. In addition, with the increase of wall thickness, the velocity of projectile acceleration reaching the maximum peak is faster.

6. Conclusions

First, simulation method can effectively analyze the penetration characteristics of honeycomb aluminum. Second, with the increase of projectile velocity, the peak acceleration increases and the acceleration pulse width increases. Third, with the increase of honeycomb aluminum wall thickness, the peak acceleration increases and the acceleration pulse width decreases. Forth, simulation method can be used to study the penetration characteristic of honeycomb aluminum and compared with experiment it has some advantages; it can makes a further optimization analysis of the structure of honeycomb aluminum.