Vibration effects on colloidal gas-liquid systems

1. Introduction

The largest-scale processes using foams are flotation and foam separation in mineral processing, as well as waste and circulating water conditioning processes in various industries. It is an essential feature of industrial flotation processes that they occur under initiated or incidental superimposed vibration [1-5]. The vibration effects on liquids and granular media have been studied quite deeply [6-7], but the literature hardly provides any information on the calculation methods and express tests for the destruction of foams and loss of foam stability under vibration. The authors of the cycle of studies on the influence of vibration effects on heterogeneous two-phase systems of water and solid fine particles [8, 9] not only demonstrate the significant effects that vibration produces on the structure of horizontal layers in such systems, but also suggest that superimposed directional vibration might affect the structure of two-phase liquid-gas systems.

Stability is one of the main characteristics of two-phase foams. Quantitative evaluation of foam stability is carried out using instrumental methods. The methods for exploring the stability of foams and establishing the foaming properties of surfactants are mainly based on studying foams in static conditions using the Ross-Miles variations, which envisage a free flow of surfactant solutions onto the surface of the same solution and measurements of the height of the resulting foam layer and the time of its destruction (the syneresis process). The Ross-Miles device and method are recommended by the International Commission on Surfactants and are specified for the Russian Federation in GOST 22567.1-77 regarding evaluation of foaming properties of detergents and in the ISO recommendations (ISO 969:1975) [10].

This paper presents an evaluation of changes in a foam layer for a two-phase system of air and a water solution of a surfactant under oscillations of the vessel with an external vibration exciter.

Sodium oleate, one of the most common flotation reagents with strong foaming properties, was used as the surfactant for the study [5]. Sodium oleate used in this work was obtained by saponification of oleic acid (GOST 7580-91) with caustic soda.

When exploring the stability of foams using anionic oxyhydryl surfactants, for example, salts of unsaturated carboxylic acids, it is necessary to take into account the micelle formation process, since the structure and properties of foams may differ significantly in pre-micellar and micellar regions [11].

The foaming effect of surfactants was evaluated by the volume of the foam and by the time of foam layer destruction to half the initial height [10]. The latter corresponds to the approach when foam evolution is regarded as a massive process of coalescence and destruction of bubbles, which is of a statistical nature. It is known that the functional dependence of foam stability on the concentration of oxyhydryl surfactants represented by soaps of unsaturated carbonate acids has two distinct maxima. One of them occurs in the region of low concentration, close to the critical micelle formation concentration (CMC). The second maximum is found in the region of complete saturation and rearrangement of adsorbed layers at the gas-liquid interface [2, 11].

The effects of vibration on the system studied were ensured using a unique specialized laboratory vibratory stand designed to study flotation processes and the behavior of colloidal systems under vibration. The model enables studying the effects of vibration on two and three-phase systems, both in continuous and intermittent regimes (see Fig. 1).

Fig. 1General view of the experimental stand: 1 – conditioning tank, 2 – shut-off fitting, 3 – interchangeable chamber, 4 – vibrating platform, 5 – vibration drives, 6 – material collecting tank

2. Results

The CMC values correlate with the foam stability data obtained using the Ross-Miles device (see Fig. 2). Experiments were carried out at different surfactant concentrations and under the two conditions (static and dynamic regimes). The first foaming maximum is explained by the highest stability of thin films with a significant gradient of surface tension due to the motion of surfactant molecules towards the film thinning area (the Marangoni effect). The maximum effect is observed in the region of concentrations close to CMC, then the foam stability decreases.

Fig. 2Foam volume and half-life vs solution concentration isotherm for the static and dynamic conditions

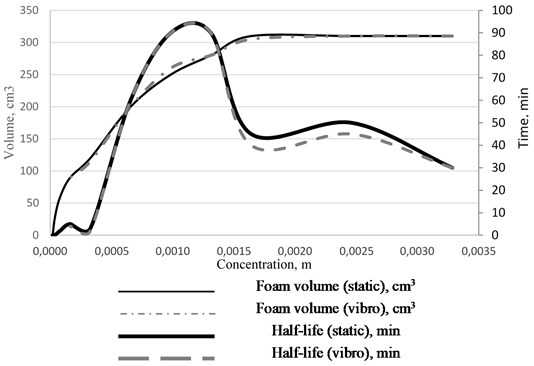
With a significant increase in the total surfactant concentration, the stability of foams increases. This is probably due to the blocking of the Gibbs channels by large micelles, which reduces the foam syneresis rate [12].

It was established that the foam volume and stability in the region of the first maximum increased with the increasing temperature of the solutions. The first foam stability maximum shifts towards higher concentrations of sodium oleate symbatically to the increase in CMC.

Similar results were obtained in the experiments studying foam stability under vibration effects on a vibrating stand. It was established that when a liquid-foam system was subjected to horizontal vibration, the half-life did not change. The same result was obtained for the vibration effects on a foam that had been cut off from the water layer.

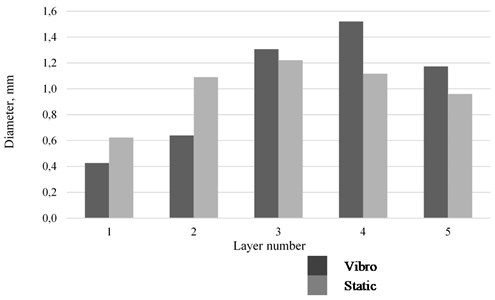
As the foam matures, it is marked by both the destruction of bubbles and changes in their size. The sizes of fine bubbles tend to decrease, while those of large bubbles increase. This phenomenon is due to the fact that, according to the laws of capillarity, the gas in fine bubbles of a foam is under greater pressure than the gas that fills large bubbles. The pressure tends to equalize by gas diffusion through the liquid film, which leads to reducing sizes of small bubbles and increasing sizes of large bubbles [13, 14]. Observations over the size distribution of bubbles were carried out under static conditions and under vibration exposure. The experiments were conducted at surfactant concentrations close to the CMC values. The bubble size was determined using an optical image analyzer based on a series of snapshots. It was found that, under oscillations in the horizontal direction with the vibration acceleration of 2.8 g, bubble segregation occurs: bubbles of smaller diameter concentrate in the lower layers (1, 2) and the bubble diameter increases (3, 4) with the height of the foam column. In static conditions, the foam layer is more uniform (see Fig. 3).

Fig. 3Size distribution of bubbles in the foam layer

3. Conclusions

In the course of the experiments, the values of the surface tension for the solutions of sodium oleate and the CMC values were determined. The relationship between foam syneresis and sodium oleate concentrations in static conditions and under vibration effects was established; structural changes in the foam layer under horizontal vibrations were observed. It was established that, under oscillations, smaller diameter bubbles would concentrate in the lower layers and that the bubble diameter would increase with the height of the foam column. The data obtained are of interest for the study and improvement of industrial processes of mineral processing by the method of flotation and foam separation and in the flotation treatment of wastewater.

Proper management of the parameters, direction and type of vibration effects on a two-phase system allows maintaining the desired foam structure. With high probability, these conclusions may be extrapolated to three-phase systems. These studies will serve as the basis for the design of vibration devices with a stable foam layer.