Abstract
This paper aims at the effects of foundation mass on the dynamic responses of beams subjected to moving oscillators. To achieve this aim, experiments were performed for a beam resting on the foundation considering effects of the foundation model including linear elastic spring, shear layer, viscous damping. In addition, special effects of mass density of foundation during vibration were established to obtain the characteristic parameter of the influence of foundation mass based on natural circular frequency of the structure system determined from FFT plots of the time history of acceleration data. Furthermore, the experimental parameters were used to analyze the influence of the foundation mass on the dynamic response of the beam subjected to moving oscillator. Comparisons between experimental and simulated results showed that the foundation mass showed significant effects on the dynamic characteristic response of the beam system. It increased the general vibrating mass of the structure system. Hence, it decreased of the natural frequency of the structural system and caused a significant increase on the dynamic response of the beam when compared with the case without considering the foundation mass. Finally, the relationships between the foundation properties and the parameters of foundation mass were derived and discussed.
Highlights
- The formulation including the experimental model was established to determine the parameter of the influence of foundation mass and expressed the dynamic response of the beam
- The detail process of the experimental model with four specimens was established to determine the influence parameter of foundation mass in the dynamic foundation model
- The experimental results reaffirmed that the influence of foundation mass significantly affected the dynamic system characteristics; It decreased the natural frequency
- The foundation mass significantly increased the dynamic responses in the ranges of various values of the speed and frequency parameters of the moving oscillator
1. Introduction
Structures resting on a foundation subjected to loads are commonly used in civil engineering. An example of these structures is the beams resting on a foundation subjected to moving vehicles such as road-foundation-vehicle, airplane-runway-foundation, track-train-foundation. Last few decades, the dynamic analysis of structures on foundation has attracted many researchers. One of well-known researchers was Winkler [1] known as pioneer in the foundation model studies, and then he was followed by Filonenko [2], Hetényi [3], Pasternak [4], Reissner [5], Kerr [6], Vlasov [7]. The Winkler model suggested quite early is one of the most fundamental elastic foundation models considering the elastic foundation stiffness as a continuous distribution of linear elastic springs, which constraint reaction per unit length at each point of the foundation is directly proportional to the deflection of the foundation itself. Therefore, this foundation model is very simple, and it has been applied so much in behavior analysis models of structures resting on foundation conducted to study the problems of the interaction of foundation and structure systems in past decades [8-20].
However, the most important deficiencies of the Winkler model appear as a displacement discontinuity between the loaded and the unloaded parts of the foundation surface while the soil surface does not show any discontinuity in reality [21]. Therefore, it does not accurately represent the characteristic response as the true behavior of foundation. Hence, several following foundation models proposed to overcome the deficiency of the Winkler model by introducing some kind of interaction between the independent springs by visualizing various types of interconnections such as an additional thin elastic membrane stretched by a constant tension (Filonenko [2]); plate with flexural rigidity (Hetenyi [3]); an incompressible layer that resists only transverse shear deformation (Pasterna [4], Reissener [5], Kerr [6]), or accounts for the effect of the neglected shear strain energy in the soil and shear forces that come from surrounding soil (Vlasov and Leont’ev [7]). These foundation models were also used widely for solving almost all discontinuity problems by analyzing the response of the structure on the foundation due to dynamic loads, moving random loads, moving oscillator as per various methods [22-35]. It can be seen that above foundation models attracted the attention of many researchers during many past decades for solving the almost all problems of structures-foundation interaction applied in many practice problems such as road-foundation-vehicle, airplane-runway-foundation, track-train-foundation. Based on literatures and achievements of these studies, the common character of these foundation models assumed that the elastic springs did not have a mass density as a mean value for these foundation models overlooked the effects of foundation mass on dynamic responses of structures-foundation interaction.
In reality, the foundation always has mass density; it also vibrates together with structures under dynamic loads. An inertial force of the foundation mass depends on the value of mass density and motion acceleration of the foundation mass and has a great effect on the system including structures and foundation. Therefore, the effects of foundation mass on the dynamic response of the above structures will also be prominent during system vibration. But many previous studies adopted above in this part do not take place to the effects of foundation mass on the dynamic analysis of structure-foundation interaction that means the inertial force from the foundation neglected in problems. Hence, the parameter of foundation mass in the dynamic problems of structures shall be mandatorily investigated in full.
Recently, a dynamic foundation model with the influence of foundation mass to analyze dynamic responses was theoretically proposed for the dynamic analysis of structures-foundation interaction [36-39]. Next, a simple experimental model was established just to check the values of the influence of foundation mass from the dynamic foundation model [40]. The experimental results also confirmed that the foundation mass had significant effects on the dynamic characteristic of the system including the structure and foundation. In addition, it decreases the natural frequency of the system without foundation mass. At the same time, the relationships between the foundation properties and the parameter of the influence of foundation mass were derived. Pham [40] presented a simple experimental model as a single degree-of-freedom system model with an elastic spring connected with lumped mass to determine the parameters of the influence of foundation mass based on the analysis of free vibration of the structure. However, the effects of foundation properties on the dynamic characteristics of the beam structure on foundation were not considered.
Hence, the aim of this study is to develop the available models by taking into account the effects of foundation properties on the dynamic response of the beam to the moving oscillator. To achieve the mentioned purpose, the formulation including the experimental models of the beam and foundation was established to determine the parameter of the influence of foundation mass and expressed the dynamic response of the beam by the finite element method. Next, the dynamic properties of structures are derived by comparing the experimental and simulated results; and then the above experimental parameters were used to analyze the dynamic response of the beam on foundation due to the moving oscillator. In order to measure the dynamic response of the beam, the dynamic magnification factor (DMF) is also defined as the ratio of the maximum time history of displacement midpoint in dynamic analysis to the displacement due to static load. Finally, the effects of the foundation mass on the dynamic response of the beam were discussed.
2. Formulation
2.1. Foundation model
Pham [36] proposed a dynamic model fully considering characteristic parameters of the foundation. These parameters include the elastic stiffness k, shear layer parameter ks, viscous damping c and mass density ρf respectively replaced by lumped mass m at the top of the elastic spring connected between the elastic layer and shear layer. This model is shown in Fig. 1.
Fig. 1Dynamic foundation model [36]: a) basic model, b) stresses in shear layer, c) force components
![Dynamic foundation model [36]: a) basic model, b) stresses in shear layer, c) force components](https://static-01.extrica.com/articles/20729/20729-img1.jpg)
Based on the principle of dynamic balance at the time t, the pressure-deflection relationship under a pressure q(x,y,t) was established as expressed in Eq. (1), in which, the functions Nx,t and Ny,t are described in Eq. (2); the forces acting on the foundation including spring, inertial and damping forces as Fig. 1c are expressed in Eq. (3) [36]:
The lumped mass m representing the foundation mass is shown in Eq. (4):
where αFis an experimental parameter of the influence of foundation mass obtained from the experimental model and HF is the depth of foundation
2.2. Experimental model
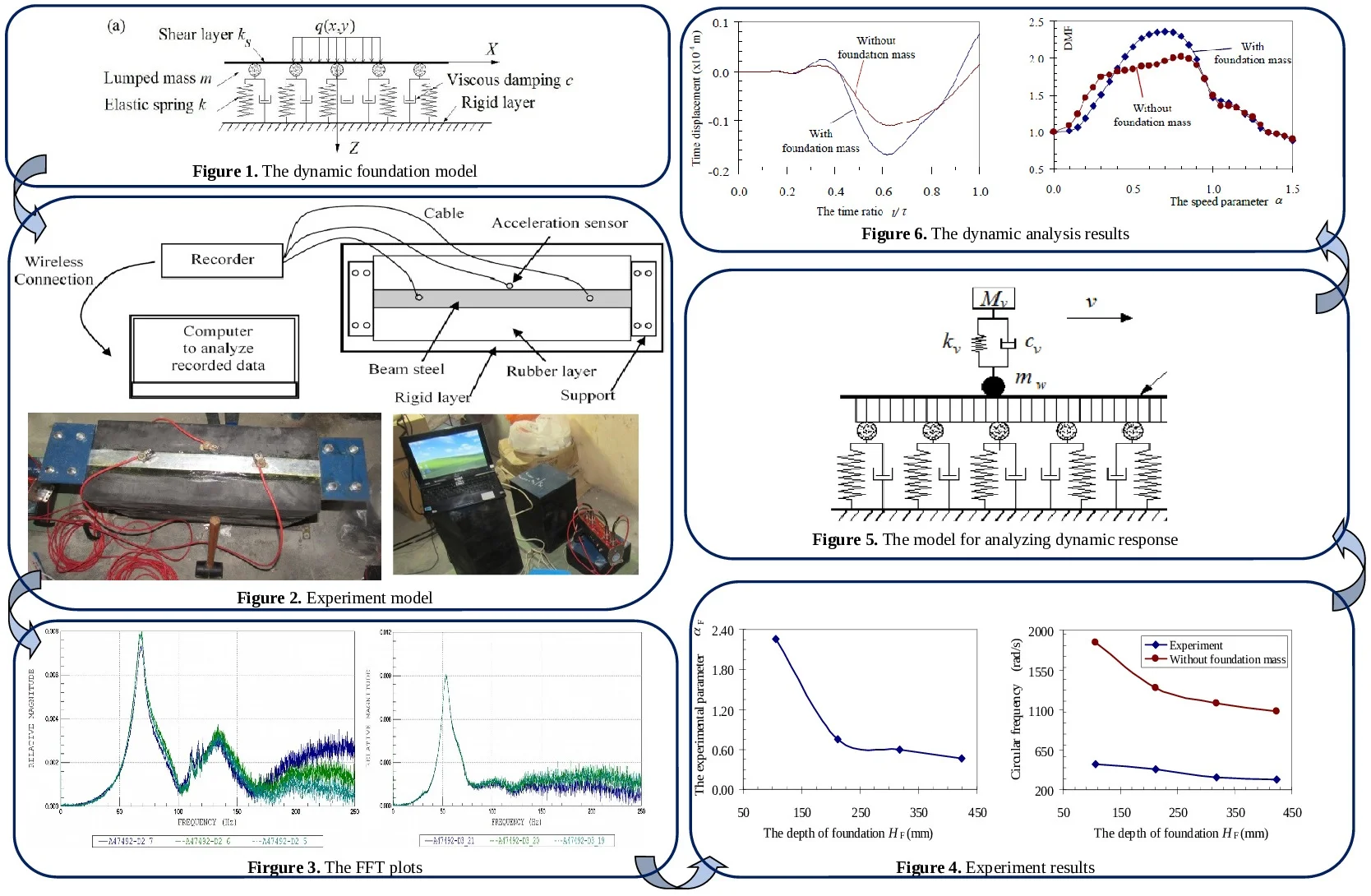
An experiment was conducted using a steel beam connected with a rubber layer representing for the dynamic foundation. The acceleration sensors were located on the surface of the steel beam and rubber layer. These sensors were connected to a vibration recorder and a computer system as shown in Fig. 2.
Fig. 2a) Detailed setup of experimental model, b) Experiment model of beam and foundation
a)

b)
The materials are specially made for the experiment. The properties of steel and rubber materials including elastic stiffness, mass density, and geometric parameters are also determined. The characteristic behaviors of the materials agrees well with the assumptions: homogeneous, continuous, isotropic and linear elastic. The steel and rubber materials can be considered as the complete materials used in the experiment aiming at analyzing the effects of foundation mass on the dynamic characteristics of beams resting on the foundation.
To analyze the free vibration of the structure system, an external force was suddenly applied on the surface of a steel beam, and then released. The acceleration time history was recorded. The data of time history acceleration were analyzed using the FFT algorithm, and the first natural frequency of the structure system can be obtained. The first natural circular frequency often occurs at the highest peak values on the FFT plot. Hence, the parameter of the influence of foundation mass αF on the dynamic characteristic of the beam can be derived based on a comparison of the first natural frequency simulated results and that of the experiment. Then, this parameter αF is used to analyze the influence of foundation mass on a dynamic analysis of the beam subjected to the moving oscillator based on the basic theory presented in the next section of the formulation chapter.
2.3. Dynamic analysis of beam on foundation
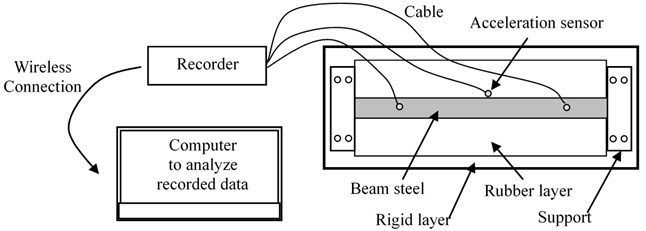
In this paper, Fig. 3 shows a clamped-clamped Euler-Bernoulli beam resting on the dynamic foundation model subjected to an oscillator moving with a constant velocity. The parameters of the oscillator model regarded as a two-node one associated with each of two concentrated masses include the stiffness kv, damping cv, the vehicle mass Mv and wheel mass mw. The mass parameter κ and the frequency parameter γ are defined in Eq. (5):
in which the mass parameter κ, is defined as the ratio of the total weight of the oscillator to the total weight of the beam Mb, and the frequency parameter γ, is defined as the ratio of the natural vibration frequency of the moving oscillator ωv to the first fundamental natural frequency of the beam ωb.
Fig. 3Model of beam resting on dynamic foundation subjected to moving oscillator
Based on the strain and kinetic energy of the beam element having two nodes including vertical displacement and rotation in global axes, the stiffness matrix Ke and mass matrix Me of the beam element are expressed in Eq. (6), followed by Eq. (7):
Mbe=∫NTwρNwdV,MFe=∫NTwmNwdx.
The damping matrix is also determined based on the dissipated energy of these disputes, expressed in Eq. (8):
It is assumed that the oscillator continuously contacts with the beam surface during its movement. Using the finite element theory, the equation of beam motion on the dynamic foundation subjected to a moving oscillator is defined as shown in Eq. (9):
where M, C and K are the overall mass, damping and stiffness matrices of the system, respectively; u(t) is the nodal displacement vector, and P(t) is the external force vector. This governing equation of the motion is used to analyze the dynamic response of beams on the dynamic foundation subjected to a moving oscillator based on the step-by-step simulation in the time domain of the Newmark algorithm. In the next chapters, the dynamic properties and responses of the system are studied for four values of the depth of foundation HF by experimental and simulated models.
3. Dynamic properties of systems
The purpose of this chapter is to determine the influence parameter of the foundation mass αF on the dynamic characteristic of the system based on the results of the natural frequency of the structure system from the experimental results and simulation by the finite element method. Three main contents are studied as follows:
– The experiment of the beam model based on four specimens carried out to determine the natural frequency;
– The numerical simulation for the influence parameter of foundation mass αF;
– The establishment of a relationship between the parameters αF and the properties of foundation as the depth of foundation HF and elastic stiffness k of four specimens.
The procedure of this problem solution including the experiment in four specimens and simulation using the finite element method is described as follows. The experiment of the structure system including steel beam on rubber foundation is conducted on four specimens with the various depth of foundation. The physical and geometric properties of the systems are given in Table 1. These properties are easily found by the other simple experiments, derived computation with acceptable results. In these experimental models, the width of the foundation is larger five times than the beam width. Therefore, the beam model on the foundation satisfies the supposition of the ideal model of the beam resting on the elastic foundation.
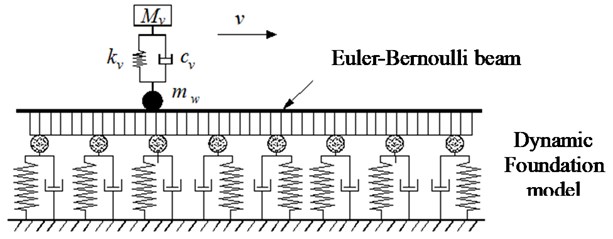
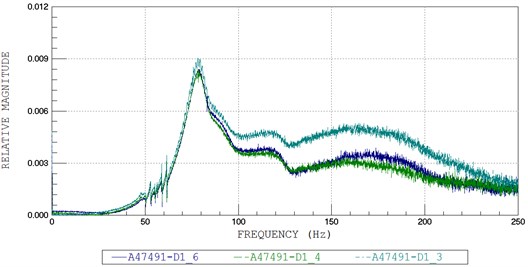
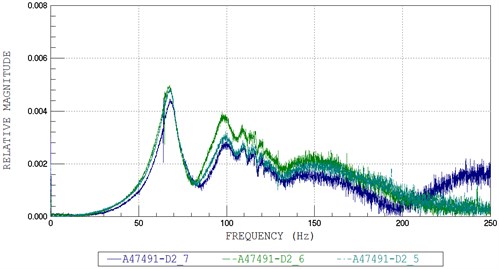
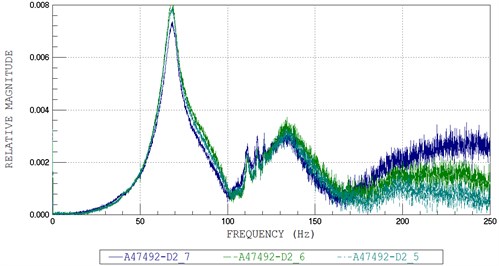
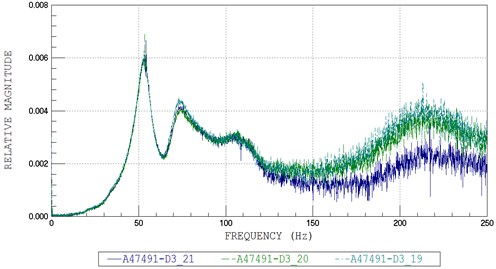
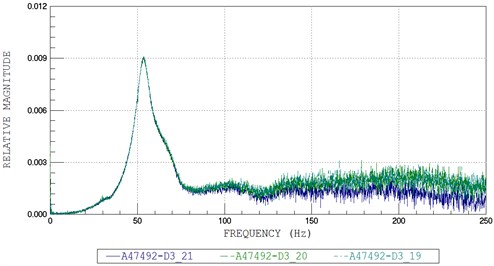
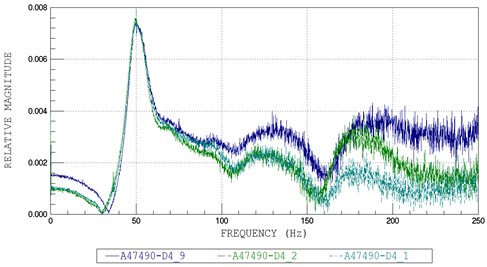
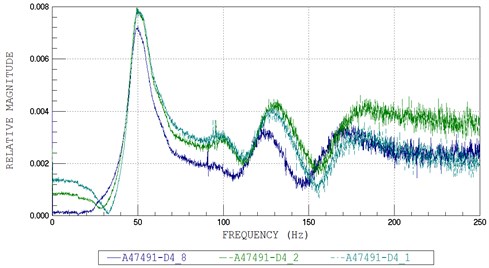
By applying a sudden external force on the surface at the middle of the steel beam, the time history of acceleration at each acceleration sensor was recorded, and then respectively the FFT plot for each acceleration sensors (A47490, A47491, and A47492) was plotted in Fig. 4 to Fig. 7.
From the FFT plots, the natural circular frequency at each acceleration sensor was twice higher than the average value. Then, the natural circular frequencies of the systems were also determined and are given in Table 2.
Fig. 4FFT plots No. 1: a) A47490, b) A47491
a)
b)
Fig. 5FFT plots No. 2: a) A47491, b) A47492
a)
b)
Fig. 6FFT plots No. 3: a) A47491, b) A47492
a)
b)
Fig. 7FFT plots No. 4: a) A47490, b) A47491
a)
b)
Table 1Properties of steel beam and rubber foundation
Length (mm) | Width (mm) | Height (mm) | ρ (kg/m3) | E (N/m2) | |||||
Steel beam | 500.00 | 40.00 | 2.80 | 7691.27 | 1.808×1011 | ||||
No. specimen of rubber foundation | HF (mm) | ρF (kg/m3) | ks (N/m) | k (N/m3) | |||||
1 | 105.98 | 1206.69 | 1.773x105 | 6.367×107 | |||||
2 | 211.96 | 2.807×107 | |||||||
3 | 317.75 | 1.874×107 | |||||||
4 | 423.64 | 1.452×107 | |||||||
Table 2Natural circular frequencies
No. Specimen | Frequencies at each acceleration sensor fF (Hz) | Circular system frequencies ω (rad/s) | ||
A47490 | A47491 | A47492 | ||
1 | 78.03 | 78.73 | 77.57 | 490.79 |
2 | 68.23 | 68.10 | 68.13 | 428.23 |
3 | 53.40 | 53.50 | 53.70 | 336.36 |
4 | 49.97 | 50.13 | 50.03 | 314.44 |
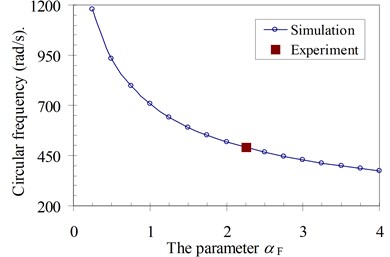
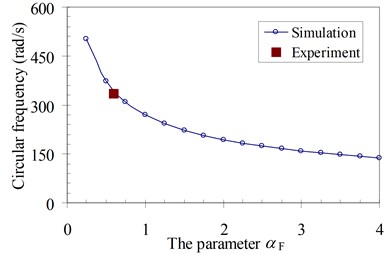
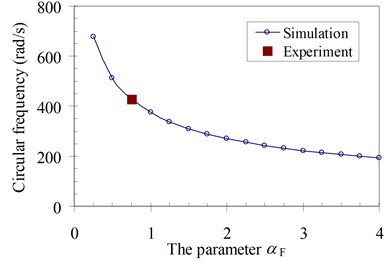
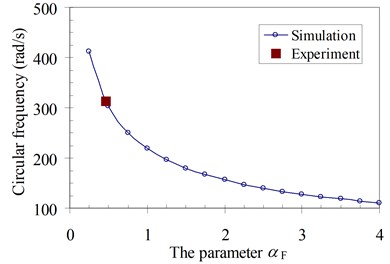
In another analysis, the simulation of the systems was also carried out. The procedure determining the natural circular frequencies of four specimens is conducted by the finite element method using Eq. (9) in case of dynamic loads and with damping force neglected. These frequencies of four specimens with the various height of foundation, which depend on the parameter of the influence of foundation mass αF, are given in Fig. 8. Based on the comparison between the experimental and simulated natural circular frequency of each specimen, the influence parameter of the foundation mass αF of four specimens was obtained in Table 3 and was also plotted in Fig. 8. Therefore, this is a physical model which is used to determine the necessary dynamic characteristics of the structure system and it can be put into the practice for a dynamic analysis of structures.
Table 3Parameters of foundation mass αF
No. specimen | HF (mm) | ω (rad/s) | αF |
1 | 105.98 | 490.79 | 2.253 |
2 | 211.96 | 428.23 | 0.748 |
3 | 317.75 | 336.36 | 0.592 |
4 | 423.64 | 314.44 | 0.461 |
Fig. 8Parameter αF of four specimens: simulation and experiment
a) No. 1
b) No. 2
c) No. 3
No. 4
Fig. 9Relationship between foundation depth HF and parameter αF
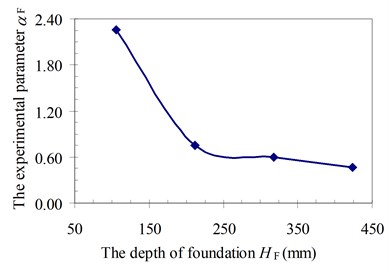
Fig. 10Relationship between depth of foundation and circular frequency ω
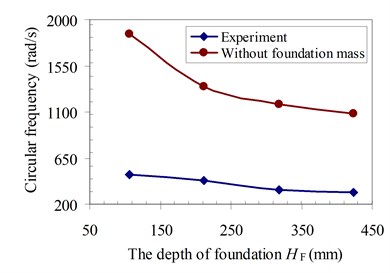
The last objective in this section is to determine the relationship between the parameter αF and the properties of foundation as the depth of foundation HF and elastic stiffness k by the experimental procedure. From the results of Table 3, the relationship between the depth of foundation HF and the parameter of foundation mass αF is plotted in Fig. 9. As can be seen in Fig. 10, the natural circular frequency of the system decreased with the increase of the depth of foundation. The experimental results agreed with the previous study of Pham [40] of a simple experiment model.
The results show that the increase in the foundation depth HF leads to the increase in the general foundation mass. However, the foundation mass participating in the vibration of the structure system was a small part of the general increasing foundation mass. Therefore, the influence parameter of foundation mass αF decreased clearly, as shown in Fig. 9. In addition, the parameter αF decreased slowly with the increase of the depth of foundation HF.
The natural frequency results of the structure system in both cases with and without the influence of the foundation mass simulated by the finite element method are presented in Fig. 10. It can be seen in Fig. 10 that the natural frequency of the structure system decreased significantly when the influence of the foundation mass was considered. It can be explained by that the foundation mass participating in the vibration of the structure system caused an increase of the vibration mass of the structure system, and therefore, the natural frequency of the structure system decreased. Moreover, an increase of the depth of the foundation HF referred to the increasing deformation as well as the stiffness of the foundation was reduced. Therefore, the structure system becomes more flexible than that one in the case without foundation mass. Fig. 10 also indicated the character dynamics of the structure system considering the influence of foundation mass. The conclusion also agrees with the previous study of Pham [40] of a simple experiment model.
The above results of this chapter show that the mass of foundation significantly affected on the dynamic characteristics of the system including beam and foundation. It was more decreasing the natural circular frequency of the system than without the effect of the foundation mass. Generally, the experimental results from four specimens showed a good agreement with behaviors of the dynamic foundation model simulated by the finite element method. The influence parameter of the foundation mass αF was completely determined based on the experimental model used in the next step for a dynamic analysis. In order words, the mass of foundation could not be neglected in analyzing the dynamic response of the beam on foundation subjected to a moving oscillator in the next section. The simulated investigation results from the mass of foundation determined by the experiments and without the effect of foundation mass clearly showed the influence of the foundation mass on the dynamic response of the beam subjected to the moving oscillator.
4. Simulation of dynamic responses
Based on the experimental results, the influence parameters of foundation mass αF representing with each specimen were determined in the previous chapter. The objective of this chapter consists in continuous consideration of the influence of the foundation mass on dynamic behaviors of the clamped-clamped beam on the foundation to moving oscillator with four specimens using a simulation of the analytical model by finite element method given in governing equation of motion Eq. (9), as shown in Fig. 3. Besides, the speed parameter α is defined as a ratio of the load speed v to the critical speed of the beam vcr, expressed as:
where the critical speed of the beam vcr is defined by the length of the beam L and the first natural circular frequency of the system ω as:
Firstly, the moving oscillator model affected the wheel mass and damping coefficients on the dynamic beam response. And then, the effects of the influence parameter of foundation mass αF on the time history displacement at the midpoint of the beam in each specimen were investigated for various speed parameters α with κ=1 and γ=1 and plotted in Fig. 11 to Fig. 14.
Fig. 11Time history displacements of midpoint of beam 1st specimen (blue – with, red – without foundation mass)
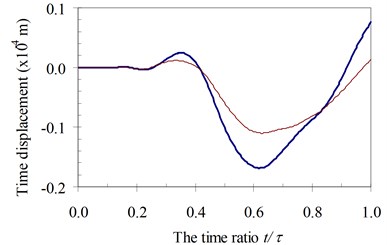
a)α=0.25
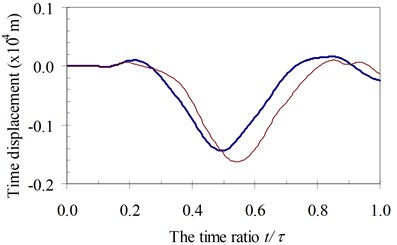
b)α=0.5
It can be seen in Fig. 11 to Fig. 14 that the foundation mass has effects on the dynamic response of the beam. Within the speed range of parameter α in all of four specimens, due to the total masses of the structure system increasing, the general vibrating mass of the structure system and then the dynamic characteristic of the system are changed. In other words, the foundation mass changed the resonant domain between the structure system and the moving oscillator compared to it without foundation mass. Hence, the foundation mass increased or decreased the time history displacement of the beam than without effects of the foundation mass with various speed parameters.
Fig. 12Time history displacements of midpoint of beam 2nd specimen (blue – with, red – without foundation mass)
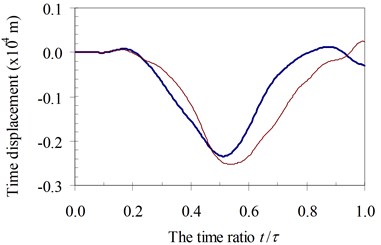
a)α=0.25
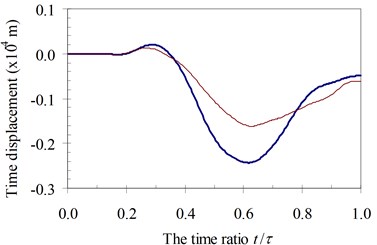
b)α=0.5
Fig. 13Time history displacements of midpoint of beam 3rd specimen (blue – with, red – without foundation mass)
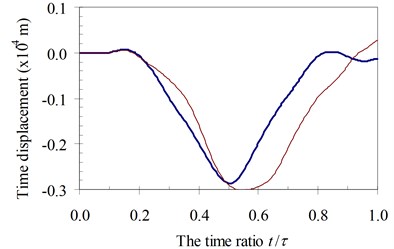
a)α=0.25
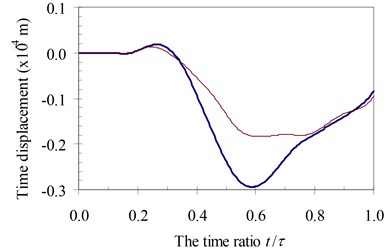
b)α=0. 5
Fig. 14Time history displacements of midpoint of beam 4th specimen (blue – with, red – without foundation mass)
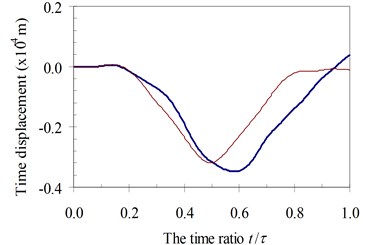
a)α=0.25
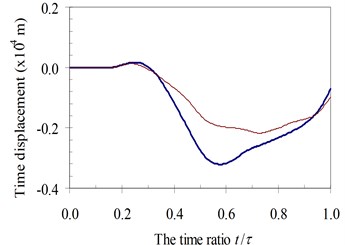
b)α=0.5
Secondly, to estimate generally the influence of the foundation mass on the dynamic response of the beam compared to without foundation mass, the values of the dynamic magnification factor were investigated in the following section for all four specimens. The effects of masses of the moving oscillator expressed by κ parameter, which is controlled by the mass of the vehicle Mv and the mass of the wheel mw as shown in Eq. (5) to DMF of the structure system with various speed parameters of four specimens were plotted in Fig. 15 to Fig. 18, respectively. These results reveal that the foundation mass significantly affects the dynamic response of the beam when compared with the case without foundation mass. Interestingly, it increased the DMF of the structure system more significantly than in the case without effects of the foundation mass in all four specimens. This increase was clearly indicated in the case of increasing of the masses of the moving oscillator as shown in Fig. 15 to Fig. 18 with various values of κ parameter.
Fig. 15DMF with various speed parameters of beam 1st specimen (blue – with, red – without foundation mass)
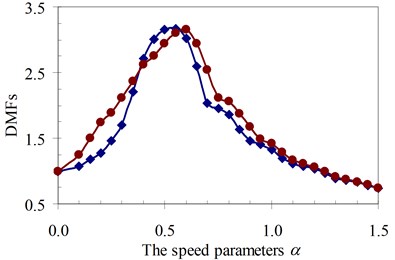
a)κ= 0.5
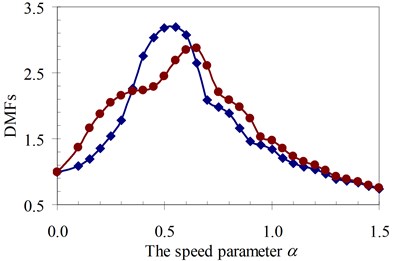
b)κ= 1
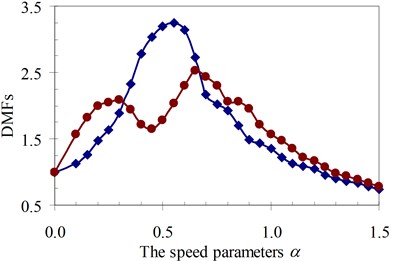
c)κ= 1.5
d)κ= 2
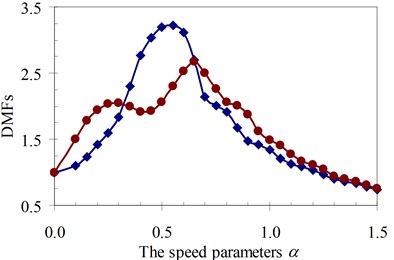
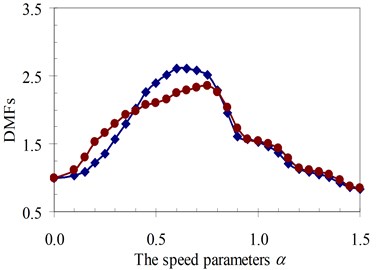
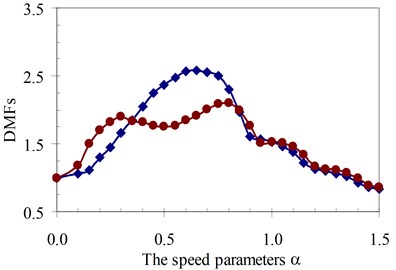
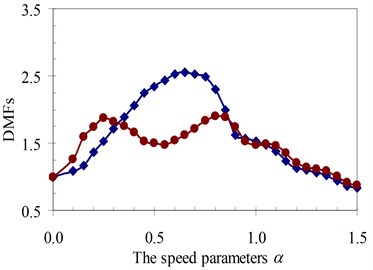
Fig. 16DMF with various speed parameters of beam 2nd specimen (blue – with, red – without foundation mass)
a)κ= 0.5
b)κ= 1
c)κ= 1.5
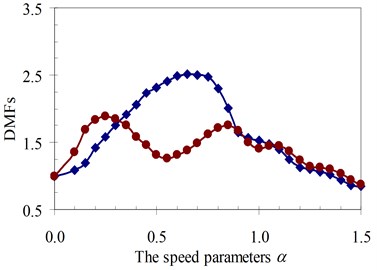
d)κ= 2
Fig. 17DMF with various speed parameters of beam 3rd specimen (blue – with, red – without foundation mass)
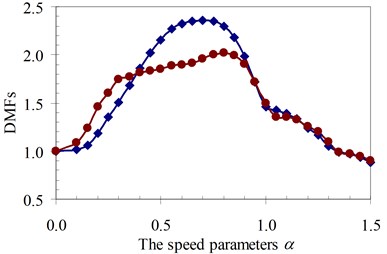
a)κ= 0.5
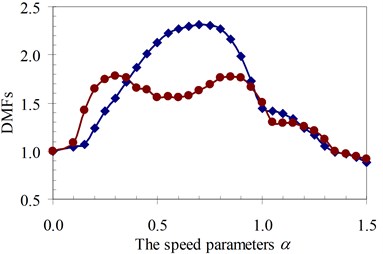
b)κ= 1
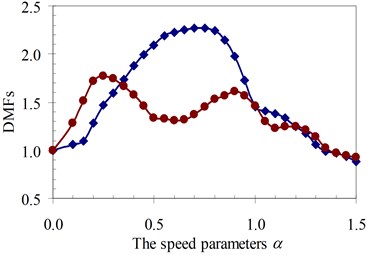
c)κ= 1.5
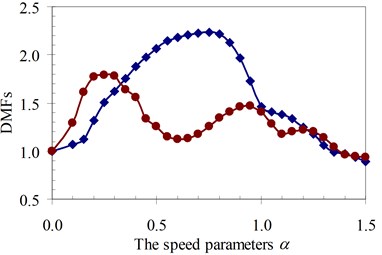
d)κ= 2
Fig. 18DMF with various speed parameters of the beam 4th specimen (blue – with, red – without foundation mass)
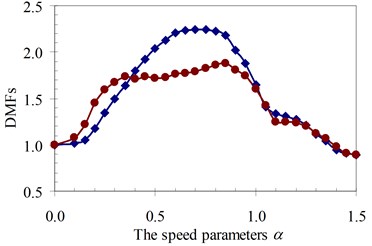
a)κ= 0.5
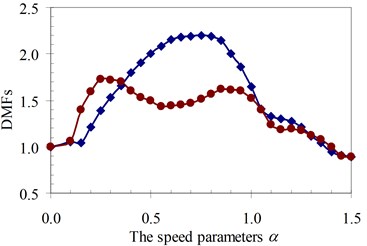
b)κ= 1
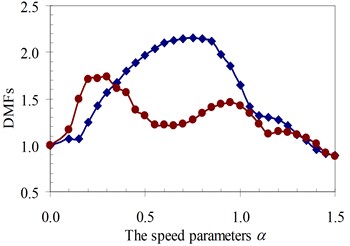
c)κ= 1.5
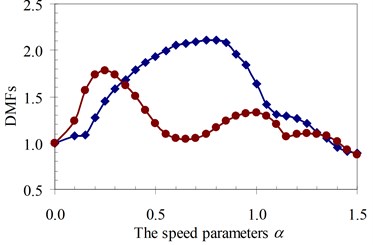
d)κ= 2
Fig. 19DMF with various speed parameters of beam 1st specimen (blue – with, red – without foundation mass)
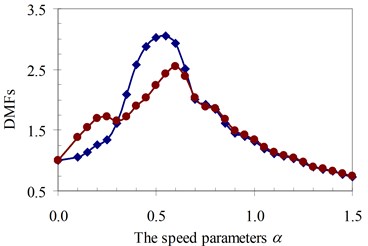
a)γ= 0.5
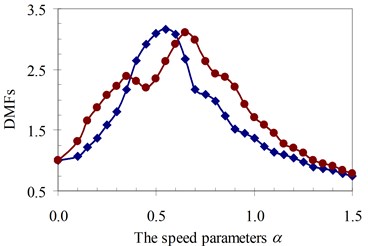
b)γ= 1.5
Fig. 20DMF with various speed parameters of beam 2nd specimen (blue – with, red – without foundation mass)
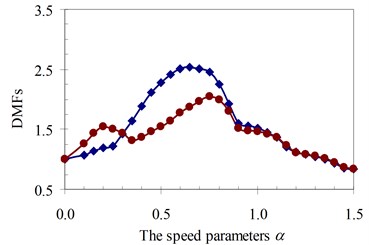
a)γ= 0.5
b)γ= 1.5
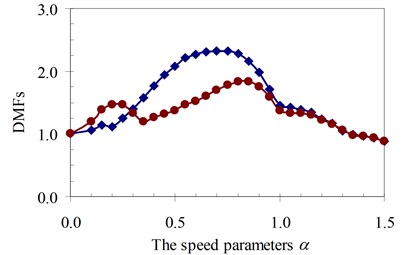
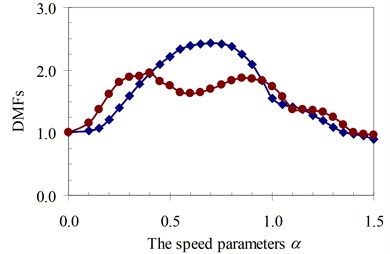
Fig. 21DMF with various speed parameters of beam 3rd specimen (blue – with, red – without foundation mass)
a)γ= 0.5
b)γ= 1.5
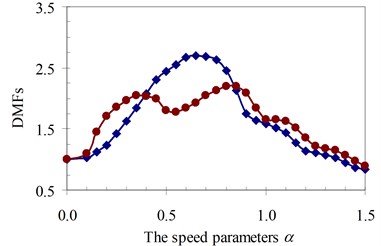
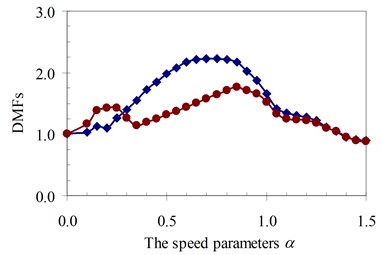
Fig. 22DMF with various speed parameters of beam 4th specimen (blue – with, red – without foundation mass)
a)γ= 0.5
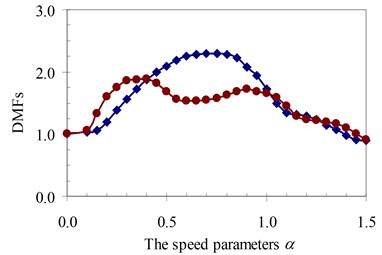
b)γ= 1.5
Similarly, the circular frequency effect of the moving oscillator on the dynamic beam response was examined. The frequency ratio γ described this property is defined as the ratio of the circular frequency of moving oscillator to the circular frequency of the structural system as Eq. (5). The DMFs of the structural system with various speed parameters of four specimens are plotted in Fig. 19 to Fig. 22, respectively. The foundation mass increased the dynamic beam response when compared with the case without foundation mass in the speed range of parameter α and frequency ratio γ. The similar remark as the previous parameter was derived and is shown in Fig. 19 to Fig. 22. The increases in DMF were higher when the foundation mass was considered.
It can be seen that the influence of the foundation mass on the dynamic beam response in each experiment specimen has difference with various values of the characteristic parameters and velocities of the moving oscillator shown in Figs. 15-22. The comparisons show that the foundation mass affects significantly the characteristic beam dynamics in all specimens, it increases clearly the dynamic beam response with an increase of the characteristic parameters of the moving oscillator (κ and γ). Within a range of high-speed parameters (α>1), the influence of the foundation mass on the dynamic response of the beam is not almost more significant than without effects of the foundation mass in the all specimens with various values of the characteristic parameters of the moving oscillator. However, the influence of the foundation mass causing an increase of the dynamic beam response in all specimens is the clearest in a range of low-speed parameters (α≤1). Especially, it increases more significantly the DMF of the beam than without effects of the foundation mass during beam vibration within the range of speed parameters (0.5≤α≤1) in the all specimens, shown in Figs. 15-22.
Therefore, it is concluded that the foundation mass demonstrated its important role in the vibration of the structure system including beam and foundation. It increases the general vibrating mass of the structure system and caused the natural frequency to reduce. Therefore, due to the action of moving oscillator, the dynamic response of the structure system was significantly changed as the resonant domain in DMF Figures moved, and the dynamic beam displacement increased significantly and was clearly compared to the case without effects of the foundation mass.
5. Conclusions
Based on the experiments and estimations of the influence of the foundation mass on the dynamic response of a beam resting on the foundation subjected to the moving oscillator, the following conclusions can be drawn:
1) The detail process of the experimental model including beam and foundation with four specimens was established to determine the influence parameter of foundation mass in the dynamic foundation model used for calculating the beam response on the foundation subjected to the moving oscillator.
2) The experimental results reaffirmed that the influence of foundation mass significantly affected the dynamic system characteristics. It increased the general vibrating system mass and then it decreased the natural frequency. Moreover, the relationships between the foundation properties and the parameter of the influence of foundation mass were derived.
3) The estimation results from the dynamic analysis of the beams show that the foundation mass significantly increased the dynamic responses in the ranges of various values of the speed and frequency parameters of the moving oscillator.
The effects of foundation mass on the dynamic response of structures is always a practical problem. Further investigation of the effects of the foundation mass on the dynamic response of the structures is encouraged.
References
-
Winkler E. Die Lehre von der Elastizitat und Festigkeit, Dominicus, Prague, 1867.
-
Filonenko-Borodich M. M. Some Approximate Theories of Elastic Foundation. Uchenyie Zapiski Moskovskogo Gosudarstvennogo Universiteta Mekhanica, Vol. 46, 1940, p. 3-18.
-
Hetényi M. Beams on Elastic Foundation Theory with Applications in the Fields of Civil and Mechanical Engineering. University of Michigan Press, Ann Arbor, Michigan, 1946.
-
Pasternak P. L. On a new method of analysis of an elastic foundation by means of two constants. Gosudarstvennoe Izdatelstvo Literaturi po Stroitelstvui Arkhitekture, Moscow, 1954.
-
Reissner E. A note on deflections of plates on a viscoelastic foundation. Journal of Applied Mechanics, Vol. 25, 1958, p. 144-155.
-
Kerr A. D. Elastic and viscoelastic foundation models. Journal of Applied Mechanics, Vol. 31, 1964, p. 491-498.
-
Vlasov V. Z., Leont’ev U. N. Beams, plates and shells on elastic foundations. Israel Program for Scientific Translation, Jerusalem, Israel, 1966.
-
Ansari M., Esmailzadeh E., Younesian D. Frequency analysis of finite beams on nonlinear Kelvin-Voight foundation under moving loads. Journal of Sound and Vibration, Vol. 330, 2011, p. 1455-1471.
-
Coşkun S. B., Öztürk B., Mutman U. Adomian decomposition method for vibration of nonuniform euler beams on elastic foundation. Proceedings of the 9th International Conference on Structural Dynamics, 2014.
-
Eisenberger M. Vibration frequencies for beams on variable one- and two-parameter elastic foundations. Journal of Sound and Vibrations, Vol. 176, Issue 5, 1994, p. 577-584.
-
Froio D., Rizzi E., Simoes F. M. F., Costa A. P. Critical velocities of a beam on nonlinear elastic foundation under harmonic. Procedia Engineering, Vol. 199, 2017, p. 2585-2590.
-
Janco R. Solution methods for beam and frames on elastic foundation using the finite element method. International Scientific Conference MSFE, 2010.
-
Jang T. S. A new semi-analytical approach to large deflections of Bernoulli-Euler-v. Karman beams on a linear elastic foundation Nonlinear analysis of infinite beams. International Journal of Mechanical Sciences, Vol. 66, 2013, p. 22-32.
-
Jorge P. C., Simoes F. M. F., Costa A. P. Dynamics of beams on non-uniform nonlinear foundations subjected to moving loads. Computers and Structures, Vol. 148, 2015, p. 26-34.
-
Jorge P. C., Costa A. P., Simoes F. M. F. Finite element dynamic analysis of finite beams on a bilinear foundation under a moving load. Journal of Sound and Vibration, Vol. 346, 2015, p. 328-344.
-
Kacar A., Tan H. T., Kaya M. O. Free vibration analysis of beams on variable Winkler elastic foundation by using the differential transform method. Mathematical and Computational Applications, Vol. 16, Issue 3, 2011, p. 773-783.
-
Kim J. S., Kim M. K. Dynamic response of an Euler-Bernoulli beam on an elastic foundation by finite element analysis using the exact stiffness matrix. Modern Practice in Stress and Vibration Analysis, Journal of Physics Conference Series, Vol. 382, 2012, p. 012008.
-
Rodrigues C., Simoes F. M. F., Costa A. P., Froio D., Rizzi E. Finite element dynamic analysis of beams on nonlinear elastic foundations under a moving oscillator. European Journal of Mechanics /A Solids, Vol. 68, 2018, p. 9-24.
-
Younesian D., Saadatnia Z., Askari H. Analytical solutions for free oscillations of beams on nonlinear elastic foundations using the variational iteration method. Journal of Theoretical and Applied Mechanics, Vol. 50, Issue 2, 2012, p. 639-652.
-
Zhou S., Song G., Wang R., Ren Z., Wen B. Nonlinear dynamic analysis for coupled vehicle-bridge vibration system on nonlinear foundation. Mechanical Systems and Signal Processing Part A, Vol. 87, 2017, p. 259-278.
-
Teodoru I. B., Muşat V. Modified Vlasov foundation model: an attractive approach for beams resting on elastic supports. EJCE, Vol. 15, 2010, p. 1-13.
-
Andrea N., Luca L. Contact problem of beams resting on tensionless two-parameter foundations. Proceedings of the 20th AMIETA Congress, Bolognia, Italy, 2011.
-
Attar M., Karrech A., Regenauer-Lieb K. Free vibration analysis of a cracked shear deformable beam on a two-parameter elastic foundation using a lattice spring model. Journal of Sound and Vibration, Vol. 333, 2014, p. 2359-2377.
-
Cao T. N. T., Reddy J. N., Ang K. K., Luong V. H., Tran M. T., Dai J. Dynamic analysis of three-dimensional high-speed train-track model using moving element method. Advances in Structural Engineering, Vol. 21, Issue 6, 2018, p. 862-876.
-
Ding H., Shi K. L., Chen L. Q., Yang S. P. Dynamic response of an infinite Timoshenko beam on a nonlinear viscoelastic foundation to a moving load. Nonlinear Dynamic, Vol. 73, 2013, p. 285-298.
-
Fallah A., Aghdam M. M. Nonlinear free vibration and post-buckling analysis of functionally graded beams on nonlinear elastic foundation. European Journal of Mechanics A/Solids, Vol. 30, Issue 4, 2011, p. 571-583.
-
Hassan M. T., Nassar M. Analysis of stressed Timoshenko beams on two parameter foundations. KSCE Journal of Civil Engineering, Vol. 19, Issue 1, 2015, p. 173-179.
-
Matsunaga H. Vibration and buckling of deep beam-columns on two-parameter elastic foundations. Journal of Sound and Vibration, Vol. 228, Issue 2, 1999, p. 359-376.
-
Morfidis K. Vibration of Timoshenko beams on three-parameter elastic foundation. Computers and Structures, Vol. 88, 2010, p. 294-308.
-
Sapountzakis E. J., Kampitsis A. E. Nonlinear analysis of shear deformable beam-columns partially supported on tensionless three-parameter foundation. Archive of Applied Mechanics, Vol. 81, Issue 12, 2011, p. 1833-1851.
-
Uzzal R. U. A., Bhat R. B., Ahmed W. Dynamic response of a beam subjected to moving load and moving mass supported by Pasternak foundation. Shock and Vibration, Vol. 19, 2012, p. 205-220.
-
Yokoyama T. Vibration analysis of timoshenko beam-columns on two-parameter elastic foundations. Computers and Structures, Vol. 61, Issue 6, 1996, p. 995-1007.
-
Zhang Y. Tensionless contact of a finite beam resting on Reissner foundation. International Journal of Mechanical Sciences, Vol. 50, 2008, p. 1035-1041.
-
Zhao Y., Si L.T., Ouyang H. Dynamic analysis of an infinitely long beam resting on a Kelvin foundation under moving random loads. Shock and Vibration, Vol. 2017, 2017, p. 3809415.
-
Zhou D., Cheung Y. K., Lo S. H., Au F. T. K. Three-dimensional vibration analysis of rectangular thick plates on Pasternak foundation. International Journal for Numerical Methods in Engineering, Vol. 59, 2004, p. 1313-1334.
-
Pham D. T., Hoang P. H., Nguyen T. P. Dynamic response of beam on a new foundation model subjected to a moving oscillator by finite element method. 16th Asia Pacific Vibration Conference APVC2015, Hanoi, Vietnam, 2015.
-
Nguyen T. P., Pham D. T., Hoang P. H. A dynamic foundation model for the analysis of plates on foundation to a moving oscillator. Structural Engineering and Mechanics, Vol. 6, 2016, p. 1019-1035.
-
Nguyen T. P., Pham D. T. The influence of mass of two-parameter elastic foundation on dynamic responses of beams subjected to a moving mass. KSCE Journal of Civil Engineering, Vol. 20, Issue 7, 2016, p. 2842-2848.
-
Nguyen T. P., Pham D. T., Hoang P. H. A new foundation model for dynamic analysis of beams on nonlinear foundation subjected to a moving mass. Procedia Engineering, Vol. 142, 2016, p. 168-174.
-
Pham D. T., Hoang P. H., Nguyen T. P. Experiments on influence of foundation mass on dynamic characteristic of structures. Structural Engineering and Mechanics, Vol. 65, Issue 5, 2018, p. 505-512.
Cited by
About this article
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 107.01-2017.23.

