Probability weighted four-point arc imaging algorithm for time-reversed lamb wave damage detection

Cao, Shuhao; Lu, Yu; Zhang, Hanfei; Xia, Qingwei; Liu, Yanyan; Ma, Shiwei

doi:10.21595/vp.2018.20467

Vibroengineering Procedia

Browse Procedia

Published: 15 March 2019

Check for updates

Probability weighted four-point arc imaging algorithm for time-reversed lamb wave damage detection

Shuhao Cao¹

Yu Lu²

Hanfei Zhang³

Qingwei Xia⁴

Yanyan Liu⁵

Shiwei Ma⁶

^{1, 2, 3, 4, 5, 6}Shanghai University, Shanghai, China

Corresponding Author:

Shiwei Ma

Cite the article Download PDF

Downloads 1480

CrossRef Citations 3

Abstract

Damage imaging based on scattering signals of ultrasonic Lamb waves in plate structure is considered as one of the most effective ways for structural health monitoring area. To improve location accuracy and reduce the impact of artifacts, a probability weighted four-point arc imaging algorithm for time reversal Lamb wave damage detection is proposed in this paper. By taking the defect as a secondary wave source, the four-point arc positioning method is used to calculate the propagation time of the signal from transducer to defect. And the amplitude of damage signal corresponding to the time of flight is used for imaging. In order to eliminate the artifacts, a damage probability weighting is combined with four-point circular arc imaging algorithm. The effectiveness of the proposed method is experimentally verified in aluminum plate. Experimental results indicate that damage location accuracy and imaging quality has been improved in both single-flaw and double-flaw samples compared with conventional delay-and-sum method.

Probability weighted four-point arc imaging algorithm for time-reversed lamb wave damage detection

Highlights

Use the flight time of Lamb wave scattering signals to image the damages
Combine the four-point arc imaging method and damage index probability imaging together
Time reversal method is used to refocus energy and increase signal-to-noise ratio
Our algorithm has been verified through the experiment on aluminum plates

1. Introduction

Structural health monitoring (SHM) has been a considerable research area for material integrity nondestructive inspecting. In this area, structure interrogation using Lamb wave can be done with transducers fixed on plate surface, which is convenient in practical applications. It is of great significance to quality inspections of industry products, especially in the plate like structure detection [1-3].

Lamb wave can spread between two surfaces of plate structure and scatter at the flaw. The defect information is acquired from the received signals which are collected by ultrasonic transducers fixed on the plate. Through imaging methods, the defect position is shown after processing the received signals. Wang et al. [4] proposed a delay-and-sum (DAS) algorithm which effectively imaged the received signals, but it made artifacts in the case of multiple defects. Sohn et al. [5] explored the correlation between the damage condition and the similarity of the reconstruct and excitation signal, and proposed the concept of damage index (DI) to characterize the severity of defect without baseline signal. Zenghua Liu et al. [6] yield a baseline-free detection method combined with the modified damage imaging algorithm based on the time reversal method. Xin Li et al. [7] proposed an acoustic emission source locating method based on time reversal theory by using four-point arc location algorithm. The efficiency of this methodology had been verified through experiments, and results showed the enhancement of damage signal energy. But the artifacts can be produced through this method.

In our paper, a new probability weighted algorithm based on the four-point arc location method is proposed. The new algorithm has been verified by the experiment, and the position of damage can be shown accurately through time reversal reconstruction signal in the detected area.

2. Principle of four-point arc location method

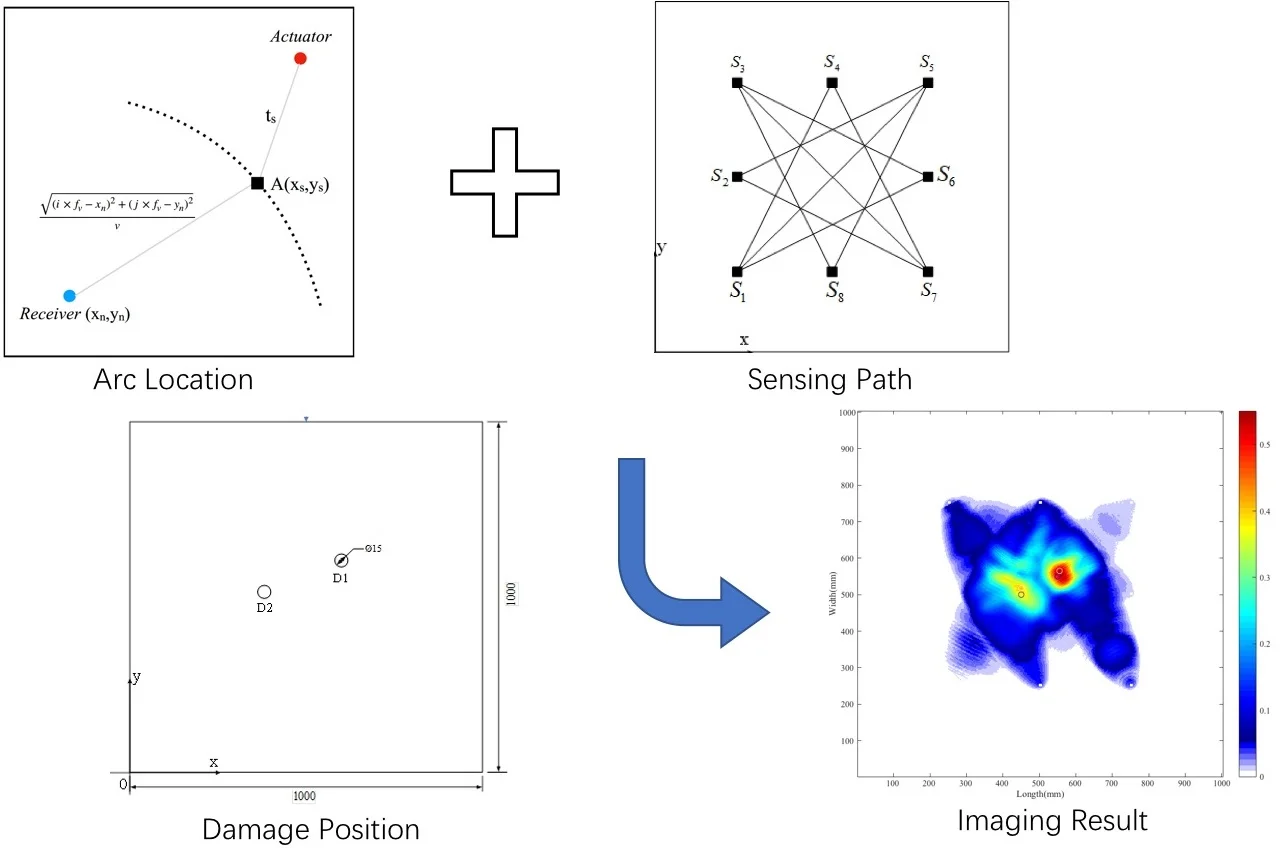
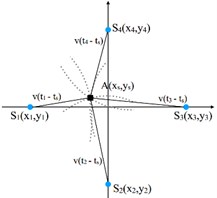
Four-point arc location algorithm is an active damage monitoring method [8]. Supposing four transducers are fixed in the four corners of a squire measured area in a plate, if the time of arriving at the receivers is known, the time of arriving at the flaw, $t_{s}$ , can be calculated by Eq. (1):

1

\{\begin{matrix} \begin{matrix} {(x_{s} - x_{1})}^{2} + {(y_{s} - y_{1})}^{2} = v^{2} {(t_{1} - t_{s})}^{2}, \\ {(x_{s} - x_{2})}^{2} + {(y_{s} - y_{2})}^{2} = v^{2} {(t_{2} - t_{s})}^{2}, \end{matrix} \\ \begin{matrix} {(x_{s} - x_{3})}^{2} + {(y_{s} - y_{3})}^{2} = v^{2} {(t_{3} - t_{s})}^{2}, \\ {(x_{s} - x_{4})}^{2} + {(y_{s} - y_{3})}^{2} = v^{2} {(t_{4} - t_{s})}^{2}, \end{matrix} \end{matrix}

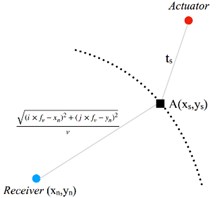
where ( $x_{s}$ , $y_{s}$ ) is the defect coordinate, ( $x_{1}$ , $y_{1}$ ) is the first transducer coordinate, $v$ is the structure wave velocity, and $t_{1}$ is the time of the signal arriving at the first transducer. ( $x_{2}$ , $y_{2}$ ), ( $x_{3}$ , $y_{3}$ ), ( $x_{4}$ , $y_{4}$ ), $t_{2}$ , $t_{3}$ and $t_{4}$ are similar defined. The flaw position and the time of arrival at the defect can be calculated by solving the equations. The principle of four-point arc location method is shown in Fig. 1(a), where A is the damage point. And then, the received signal can get imaged referring to the calculation results as shown in Eq. (2):

2

S_{i j} = \sum_{n = 1}^{N} A_{n} \cdot f_{n} (t_{s} + \frac{R_{i j n}}{v}), R_{i j n} = \sqrt{{(i \times f_{v} - x_{n})}^{2} + {(j \times f_{v} - y_{n})}^{2}},

where $S_{i j}$ is the damage imaging value of the position ( $i$ , $j$ ), $N$ is the number of the signal, $A_{n}$ is a coefficient for balancing the transducers’ output, $R_{i j n}$ is the distance of transducer ( $x_{n}$ , $y_{n}$ ) and measure point ( $i$ , $j$ ) and $f_{v}$ is image resolution. The defect is seen as an acoustic secondary source according to the time $t_{s}$ . The schematic of the imaging method is presented in Fig. 1(b).

Fig. 1Illustration of four-point arc imaging method

a) Location schematic

b) Imaging principle

3. Proposed method

3.1. Damage index probability imaging

The time reversal method is an application of the acoustic reciprocity principle, which can effectively reconstruct the sound source signal [9]. After the time reversal process, the received signal, should have the same shape with the original one, which is called signal reconstruction.

Referring to the time reversal theory, if certain kinds of defects present, the linear reciprocity property will break down, making the reconstructed signal deviate from the input original signal [5]. Due to this property, the damage index is introduced to quantify the deviation of the two signals [10]. Damage index is calculated by Eq. (3):

3

D I_{n} = 1 - \sqrt{{[\int_{t_{0}}^{t_{1}} V_{a} (t) V_{r} (t) d t]}^{2} / \int_{t_{0}}^{t_{1}} V_{a}^{2} (t) d t \int_{t_{0}}^{t_{1}} V_{r}^{2} (t) d t},

where $n$ denotes the $n$ th damage sensing path, $t_{0}$ , $t_{1}$ are the signal time of beginning and ending. The defect probability $P$ at a specific position ( $x$ , $y$ ) is defined by Eq. (4) as follows:

4

P (x, y) = \sum_{n = 1}^{N} p_{n} (x, y) = \sum_{n = 1}^{N} D I_{n} W_{n} [R_{n} (x, y)],

where $W_{n} [R_{n} (x, y)]$ is the probability distribution. Sheen et al. [11] indicated that the longer distance from damage to sensing path related smaller damage index. The distribution function is:

5

W_{n} [R_{n} (x, y)] = \{\begin{array}{l} 1 - \frac{R_{n (x, y)}}{β}, R_{n} (x, y) < β, \\ 0, R_{n} (x, y) \geq β, \end{array}

where $β$ is a sensing area parameter of a certain path. In this paper, $β =$ 0.05. And:

6

R_{n} (x, y) = \frac{d_{A n} (x, y) + d_{R n} (x, y)}{d_{n}} - 1,

where $d_{A n}$ is the distance from ( $x$ , $y$ ) to the actuator in the $n$ th sensing path. Similarly, $d_{R n}$ is the distance to the receiver. And $d_{n}$ is the distance of the actuator and receiver. The distribution function gives the relationship between damage probability and measured position.

3.2. Damage probability weighted four-point arc imaging

The four-point arc location method has better position accuracy than the damage index weighted method, however the artifacts may produce owing to the algorithm limitation. While the probability method creates no artifacts, but it has limited location capability. In order to make full use of the defect information and acquire better imaging quality, a new weighted algorithm based on the four-point arc location method and the damage index probability method is presented. According to Eq. (4)-(6), this new weighted imaging algorithm is explained by Eq. (7):

7

S_{i j} = \sum_{n = 1}^{N} p_{n} (x, y) \cdot A_{n} f_{n} (t_{s} + \frac{R_{i j n}}{v}) = \sum_{n = 1}^{N} {D I}_{n} W_{n} [R_{n} (x, y)] \cdot A_{n} f_{n} (t_{s} + \frac{R_{i j n}}{v}) .

It is not difficult to see that Eq. (7) is the form of probability expectation. And the full summation method is used to obtain the imaging result after each of the expectation term is calculated. Under the influence of the probabilities, image of the measured area is limited by the damage probability distribution, which reduces error of the damage location. The new weighted method combines the advantages of both methods. By adding the part of probability weight, the image quality of the four-point arc imaging algorithm is improved and the image value of artifact pixel is reduced. Besides, the defects can be located more accurately.

4. Experiments

4.1. Experimental setup

The experimental system consists of a personal computer, an arbitrary waveform signal generator (Agilent 33520A), an active signal amplifier based on the TI op amp chip OPA657, and a four-channel oscilloscope (Tektronix DPO5034B). The experimental setup is shown in Fig. 2. The excitation signal is the normalized five period sinusoidal narrow-band signal modulated by Hanning window. And the signal frequency is 500 kHz. The signals are excited and received by contacting ultrasonic oblique probes.

The test samples in this experiment are two 6061 aluminum plates, which are single-flaw and double-flaw respectively. The defects are circle through hole with a diameter of 15 mm. The coordinate origin is the left bottom corner of the plate. As the Fig. 3(a) and Fig. 3(b) shows, the center coordinate of the single flaw is (550, 550) called D1, and the center coordinates of the double flaws are (450, 500) and (550, 550) called D1 and D2 respectively. During the imaging process, the measured area is divided into 400×400 = 160000 grids with the area of 2.5×2.5 mm² for each one.

The transducers are placed as shown in the Fig. 3(c), in order to reduce the influence of boundary reflection. The black blocks denote the transducers, and the links between the blocks are the 10 sensing paths. The positions of the eight probes are $S_{1}$ (250,250), $S_{2}$ (500,250), $S_{3}$ (750,250), $S_{4}$ (500,750), $S_{5}$ (750,750), $S_{6}$ (750,500), $S_{7}$ (750,250), $S_{8}$ (500,250).

Fig. 2Schematic illustration of experimental setup

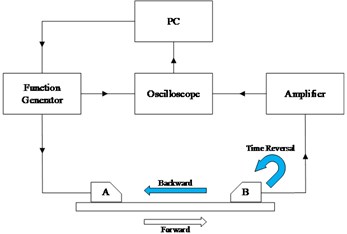
a) Experimental system

b) Transducers placement

Fig. 3Diagram of environmental sample plates

a) Single flaw sample

b) Double flaws sample

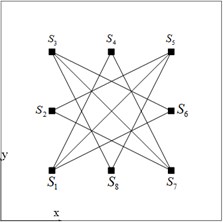
c) Sensing paths layout

4.2. Experiment processing and results

Using the experimental system above, a series of signal data related to each sensing path is obtained through the time reverse process. Then the damage index shown in Table 1 and Table 2 is calculated by Eq. (3) according to the time reversal signal. The result of the damage probability weighted four-point arc method is presented in Fig. 4(a) and Fig. 4(b). Note that white circles denote the defects acquired by the method and black circles indicate the actual defect locations. From the picture, the distance from the center of the defect acquired by the method to the real, D1, is 5 mm for the single-flaw plate; and in the double-flaw sample, the distances from the algorithm acquired to the real are 17.50 mm for the D1 and 15.81 mm for the D2. Besides, the result of the time-reverse delay-and-sum method is presented in Fig. 5(a) and Fig. 5(b). For single defect, the distance from the acquired to the real D1 is 19.04 mm; for the double damages, the distance from the acquired to the center of D1 and D2 are 29.15 mm and 34.00 mm respectively. From Fig. 5(a) and Fig. 5(b), the damage image is insufficiently precise to clearly find exact positions of the defects especially in double-defect plate. While from the Fig. 4(a) and Fig. 4(b), the flaw locations are well captured with our new weighted method, and the contrast ratio of Fig. 4(b) is higher than the Fig. 5(b). Both in Fig. 4(a) and Fig. 4(b), the maximum image value pixel can indicate the defect position clearly, and the artifact is reduced in the two-defect case compared with the DAS method.

Table 1Damage index of single flaw

Paths	$S_{4} - S_{7}$	$S_{1} - S_{5}$	$S_{1} - S_{6}$	$S_{3} - S_{6}$	$S_{3} - S_{7}$
DI	0.1402	0.1336	0.1330	0.1287	0.1242
Paths	$S_{3} - S_{8}$	$S_{2} - S_{5}$	$S_{1} - S_{4}$	$S_{2} - S_{7}$	$S_{5} - S_{8}$
DI	0.1212	0.1202	0.1189	0.1160	0.1010

Table 2Damage index of double flaws

Paths	$S_{4} - S_{7}$	$S_{1} - S_{5}$	$S_{3} - S_{7}$	$S_{1} - S_{4}$	$S_{3} - S_{6}$
DI	0.1695	0.1450	0.1429	0.1386	0.1322
Paths	$S_{3} - S_{8}$	$S_{1} - S_{6}$	$S_{2} - S_{7}$	$S_{2} - S_{5}$	$S_{5} - S_{8}$
DI	0.1299	0.1228	0.1192	0.1167	0.1129

Fig. 4Imaging results of weighted four-point arc method

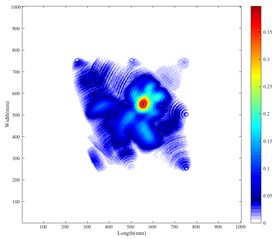
a) Weighted method in single-flaw sample

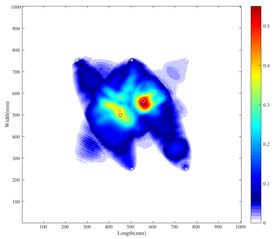
b) Weighted method in double-flaw sample

Fig. 5Imaging results of das method

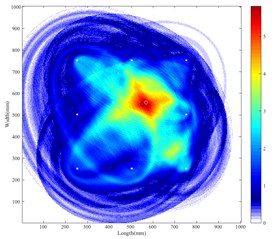
a) DAS in single-flaw sample

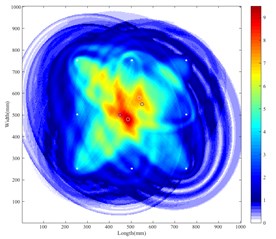
b) DAS in double-flaw sample

Fig. 6Thresholder results of weighted method

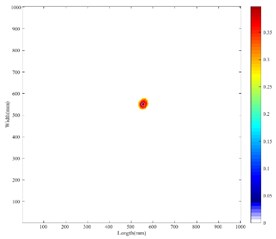
a) Weighted method in single-flaw sample

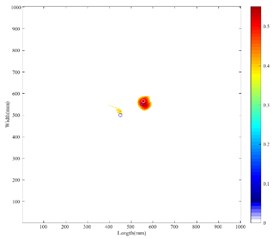
b) Weighted method in double-flaw sample

The location error of the two imaging methods is presented in Table 3 for comparison purpose. As the data in the table shows, it can be seen that the location accuracy of the weighted four-point arc imaging method is higher than the time-reversal DAS method. To facilitate observation, the image is intercepted with the threshold of the 70 % peak value. The thresholder image is shown in Fig. 6. The damage location and area detected by imaging generally match the actual damage situation. The error may produce due to the inaccuracy of group velocity, and the damage index measurement of the sensing paths. It can be limited further by more accurate velocity measurement and improved damage probability method.

Table 3Error of two algorithms

Defects	Single defect	Double defects
Algorithm	D1	D1	D2
Weighted 4-point arc	5.00 mm	17.50 mm	15.81 mm
Delay-and-sum	19.04 mm	29.15 mm	34.00 mm

5. Conclusions

The proposed method combines the advantages of four-point arc location algorithm and the damage index probability method. The time reversal process is done for the purpose of focusing the energy of the scatters, and damage index is acquired by calculating the deviation of reconstruction and original signal. Experimental result shows that the method have better location accuracy and more precise defect imaging area compared with the typical delay-and-sum method, which validates the efficiency of the proposed method. In future works, the velocity of the wave can be measured better, and the weight method can be also modified to achieve better performance.

References

Alleyne D. N., Cawley P. The interaction of Lamb waves with defects. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, Vol. 39, Issue 3, 1992, p. 381.

Publisher
Chang Z., Mal A. Scattering of Lamb waves from a rivet hole with edge cracks. Mechanics of Materials, Vol. 31, Issue 3, 1999, p. 197-204.

Publisher
Staszewski W. J., Lee B. C., Traynor R. Fatigue crack detection in metallic structures with Lamb waves and 3D laser vibrometry. Measurement Science and Technology, Vol. 18, Issue 3, 2007, p. 727.

Publisher
Wang C. H., Rose J. T., Chang F. K. A synthetic time-reversal imaging method for structural health monitoring. Smart Materials and Structures, Vol. 13, Issue 2, 2004, p. 415.

Publisher
Sohn H., Park H. W., Law K. H., et al. Damage detection in composite plates by using an enhanced time reversal method. Journal of Aerospace Engineering, Vol. 20, Issue 3, 2007, p. 141-151.

Publisher
Liu Z., Zhong X., Dong T., et al. Delamination detection in composite plates by synthesizing time-reversed Lamb waves and a modified damage imaging algorithm based on RAPID. Structural Control and Health Monitoring, Vol. 24, Issue 5, 2017, p. e1919.

Publisher
Xin Li, Gengsheng Luo, Shengrong Long, et al. Location method of acoustic emission by time reversal focusing and enhancing for steel plate. Chinese Journal of Scientific Instrument, Vol. 37, Issue 8, 2016, p. 1792-1799.

Search CrossRef
Qiang Wang, Shenfang Yuan, Lei Qiu, et al. Image representation based on time reversal theory for structure health monitoring. Chinese Journal of Scientific Instrument, Vol. 29, Issue 9, 2008, p. 1816-1821.

Search CrossRef
Park H. W., Kim S. B., Sohn H. Understanding a time reversal process in Lamb wave propagation. Wave Motion, Vol. 46, Issue 7, 2009, p. 451-467.

Publisher
Wang D., Ye L., Lu Y., et al. Probability of the presence of damage estimated from an active sensor network in a composite panel of multiple stiffeners. Composites Science and Technology, Vol. 69, Issue 13, 2009, p. 2054-2063.

Publisher
Sheen B., Cho Y. A study on quantitative lamb wave tomogram via modified RAPID algorithm with shape factor optimization. International Journal of Precision Engineering and Manufacturing, Vol. 13, Issue 5, 2012, p. 671-677.

Publisher

Cited by

Localisation of Automobile Door Rattle Noise Based on the Time Reversal Method

Weidong Zhao | Nan Zhang | Li’an Tian

(2023)

A time-reversal assisted probabilistic fusion strategy for damage localization in plate-like structures using Lamb waves

Minghui Zhang | Deyuan Zhou | Xiuquan Li | Ziqian Yang | Qingzhao Kong

(2023)

2019 IEEE Symposium Series on Computational Intelligence (SSCI)

DING Gang | PEI Xiaoyuan | LI Yunting

(2019)

About this article

Received

21 December 2018

Accepted

28 December 2018

Published

15 March 2019

SUBJECTS

Fault diagnosis based on vibration signal analysis

DOI

https://doi.org/10.21595/vp.2018.20467

Erratum

Value

Incorrect institutional affiliation of the authors. Corrected affiliation: School of Mechatronic Engineering and Automation, Shanghai University, Shanghai, China.

For more information read Editor's Note.

Keywords

damage index probability

weighted four-point arc location

time reversal

Acknowledgements

This work was supported by the National Natural Science Foundation of China with Grant No. 61671285.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2019 12 31

A modified damage index probability imaging algorithm based on delay-and-sum imaging for synthesizing time-reversed Lamb waves

Qingwei Xia, Yanyan Liu, Yu Lu, Shuhao Cao, Hanfei Zhang, Shiwei Ma

Research article

2017 11 15

Elliptical ring distribution probability-based damage imaging method for complex aircraft structures

Guoqiang Liu, Yingchun Xiao, Hua Zhang, Gexue Ren

Research article

2016 02 15

Research on lamb wave wavenumber response and PZT 2D cross-shaped array based damage imaging method of aircraft composite structures

Lei Qiu, Shenfang Yuan, Zhongqing Su, Bin Liu

Research article

2014 11 03

Omni-directional damage detection and localization with a 2-D piezoelectric ultrasonic phased array

Wang Zhiling, Yuan Shenfang, Qiu Lei, Liu Bin

S. Cao, Y. Lu, H. Zhang, Q. Xia, Y. Liu, and S. Ma, “Probability weighted four-point arc imaging algorithm for time-reversed lamb wave damage detection,” Vibroengineering PROCEDIA, Vol. 22, pp. 25–30, Mar. 2019, https://doi.org/10.21595/vp.2018.20467

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2018.20467
UR  - https://doi.org/10.21595/vp.2018.20467
TI  - Probability weighted four-point arc imaging algorithm for time-reversed lamb wave damage detection
T2  - Vibroengineering PROCEDIA
AU  - Ma, Shiwei
AU  - Cao, Shuhao
AU  - Lu, Yu
AU  - Zhang, Hanfei
AU  - Xia, Qingwei
AU  - Liu, Yanyan
PY  - 2019
DA  - 2019/03/15
PB  - JVE International Ltd.
SP  - 25-30
VL  - 22
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Ma_2019,
	doi = {10.21595/vp.2018.20467},
	url = {https://doi.org/10.21595/vp.2018.20467},
	year = 2019,
	month = {mar},
	publisher = {{JVE} International Ltd.},
	volume = {22},
	pages = {25--30},
	author = {Shiwei Ma and Shuhao Cao and Yu Lu and Hanfei Zhang and Qingwei Xia and Yanyan Liu},
	title = {Probability weighted four-point arc imaging algorithm for time-reversed lamb wave damage detection},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]S. Ma, S. Cao, Y. Lu, H. Zhang, Q. Xia, and Y. Liu, “Probability weighted four-point arc imaging algorithm for time-reversed lamb wave damage detection,” Vibroengineering PROCEDIA, vol. 22, pp. 25–30, Mar. 2019, doi: 10.21595/vp.2018.20467.

Copy IEEE

Copied to clipboard!

Ma, Shiwei, Shuhao Cao, Yu Lu, Hanfei Zhang, Qingwei Xia, and Yanyan Liu. “Probability Weighted Four-Point Arc Imaging Algorithm for Time-Reversed Lamb Wave Damage Detection.” Vibroengineering PROCEDIA 22 (March 15, 2019): 25–30. https://doi.org/10.21595/vp.2018.20467.

Copy Chicago

Copied to clipboard!

Probability weighted four-point arc imaging algorithm for time-reversed lamb wave damage detection

Abstract

Highlights

1. Introduction

2. Principle of four-point arc location method

3. Proposed method

3.1. Damage index probability imaging

3.2. Damage probability weighted four-point arc imaging

4. Experiments

4.1. Experimental setup

4.2. Experiment processing and results

5. Conclusions

References

Cited by

About this article

Related Articles