Numerical analysis of vibration-isolating effect of vibration-isolating slot under buried pipe subjected to millisecond blasting

1. Introduction

The explosive charge structure can be classified into concentrated charge and dispersive charge. Although the experts agreed that the two charge structures have different effects on the vibration effect of blasting earthquake through the long-term experiment, its internal mechanism, especially the transmission of vibration and energy in dispersive charge, hasn’t come to a clear conclusion. But the exploration of differential blasting keeps going in the Academia all the time. Wu Congshi et al. [1] analyzed the connection between millisecond blasting and the blasting vibration, concluding the appropriate interval of millisecond blasting in their own research project. Lin Dachao and Zhang Qi et al. [2] designed experiment to research millisecond blasting and blasting vibration. Namely, under 20 ms, 40 ms, 60 ms and 80 ms delay time and distance from the explosion point 10 m, 20 m and 40 m, the theoretical analysis and research on the vibration velocity and the rule of the power spectrum arrangement were studied by testing the vibration velocity on the direction vertical to the ground. According to the study, reducing ground vibration strength through millisecond blasting, there is an optimal value of delay time. Anderson [3] summarized the relationship between the delay time and the vibration mainly based on an immense amount of engineering blasting data, and expressed their relationships by gray scale. Gao Wenxue and Jin Qiankun [4] studied slot millisecond blasting of deep hole by the engineering practice and based on the study of the dynamic finite element program, and discussed the slot rock movement law and the inherent mechanism of millisecond blasting. It showed that, based on engineering practice, the dynamic situation of rock blasting fragmentation is really presented, which has become the support of blasting theory. Hewetra [5] studied underground structure stability under blasting vibration wave, analyzed influence of surrounding rocks with different properties on vibration velocity, and put forward effective vibration damping measures. Anony [6] used the finite element program to analyze the damage model of modified fragmentation effect on surrounding rock under the condition of different detonating modes, which is according to the dynamics theory. Li Xi-bing and Ling Tong-hua [7] utilized the piecewise linear interpolation method instead of analytical expression of trigonometric interpolation, which means less complication and higher accuracy in the calculation of single-segment and multi-segment millisecond blasting signal response spectrum. The results showed that single-segment and multi-segment has quite discrepant structure response to blasting vibration. In addition, the blasting seismic wave differences exist in the choice of amplification effects for the distinction of the structure, for instance, such millisecond blasting in the influence of the damping effect at the same time, increase the probability of structural response to selective amplification some of the vibrating body.

It is not a good way to do researches on vibration-isolating effect of vibration-isolating slot subjected to millisecond blasting by experiment, because blasting test cost is relatively high, the test site is special and it has a certain risk. At the same time, in view of the limited monitoring range, vibration-isolating effect of vibration-isolating slot in the actual test is also just passable. Through small blasting test in advance, it can inaccurately predict the propagation and attenuation of blasting seismic wave in the soil. As a result, direct field experiment may fail to acquire ideal effect, and even cause the waste of human resources, material and financial resources generated by more working conditions. In contrast, it is better to do research on vibration-isolating effect of vibration isolating by the numerical method without external environmental factors. It can measure data without the high experiment cost and analyze the influence of some key parameters according to the results. In the same condition, the numerical simulation cost much less than the test. Therefore, numerical simulation is an indispensable method to analyze the effect of the micro-differential blasting on shock absorbing.

2. Calculation model

The initial conditions of the numerical simulation model are determined according to the principle of maximum blasting damage effect. Considering the damage of buried pipe subjected to millisecond blasting for a certain distance from the blasting area, the calculation model is mainly produced by the homogeneous explosive charge. The distance between the charge and the axis of the pipeline is 50 m, and the pipe buried 1.2 m underground.

Fig. 1The numerical calculation model

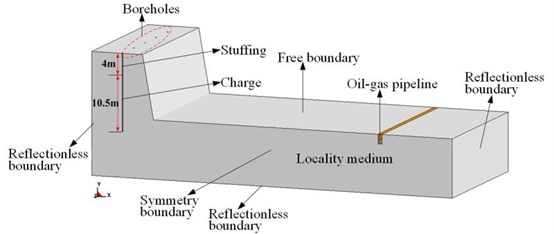
According to the characteristics of the problem studied, the coupling algorithm of multi material Euler and Lagrange structure can be applied to calculate the interaction between explosives, air and other solid structures. In the actual modeling process, it defines explosives and air as Euler grids, and ensures the common nodes among them. It defines the site medium, the fine sand in the pipe trench, the backfill soil medium and the steel pipe as the Lagrange mesh. The interaction between the fine sand in the trench and pipe adopts the surface-surface contact analysis. On contact surface in fine sand and steel pipe, steel pipe will take the master contact surface (Master Surface, for larger stiffness), and soil can be considered as the slave contact surface (Slave Surface, relatively soft). In order to improve the mesh accuracy and save computing resources, we only need to establish the 1/2 model relative to the hole axis and adopt the g-cm-s system. The meshes of explosives and surrounding rock are denser than others. Because the rock is affected by blasting seismic waves, which is in the range of elastic deformation, so the mesh could be sparse. The SOLID164 element is used to mesh the above three-dimensional numerical models. The numerical calculation model is shown in Fig. 1.

3. Numerical simulation results and analysis

Fig. 2, Fig. 3, Fig. 4 are the propagation of blasting seismic waves under the condition of no shock absorption. As the vibration velocity cloud of particle is applied, this part is more intuitionistic and clear. Fig. 2, Fig. 3 and Fig. 4 respectively represents 275 kg homogeneous explosive charge (1 hole), 1375 kg homogeneous explosive charge (5 holes) and 2475 kg homogeneous explosive charge (9 holes). The maximum vertical vibration data at the pipe location can be extracted through post-processing software. Fig. 5 is the maximum vertical vibration velocity history curve of the pipe under the condition of no vibration-isolating slot.

Fig. 2The propagation of blasting seismic waves (275 kg charge per delayed interval)

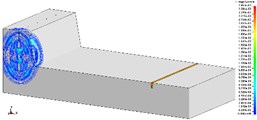
a) T1, 1/2 model

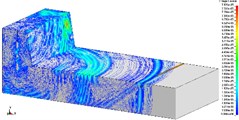
b) T2, 1/2 model

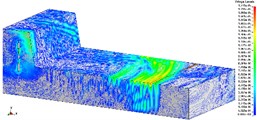
c) T3, 1/2 model

Fig. 3The propagation of blasting seismic waves (1375 kg charge per delayed interval)

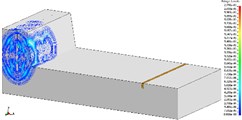
a) T1, 1/2 model

b) T2, 1/2 model

c) T3, 1/2 model

Fig. 4The propagation of blasting seismic waves (2475 kg charge per delayed interval)

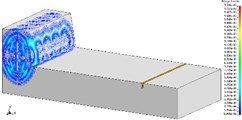
a) T1, 1/2 model

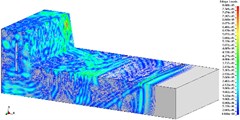
b) T2, 1/2 model

c) T3, 1/2 model

Fig. 5The vertical velocity history curve of the pipe under the condition of no vibration-isolating slot

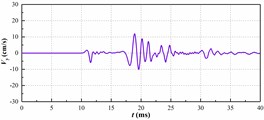
a) 275 kg charge

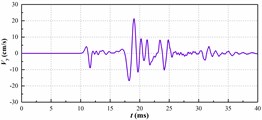
b) 1375 kg charge

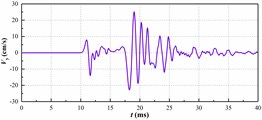
c) 2475 kg charge

The vibration peak value in each time history curve is shown in Fig. 5. The relationship between the single explosive charge and the maximum vertical vibration velocity of the pipe has been shown in Fig. 6. The graph shows that the maximum vertical vibration speed of pipeline has a positive correlation rather than linear correlation with the amount of homogeneous explosive charge. This is in accordance with the trend reflected by the prediction formula of blasting seismic peak value which is proposed by the national standard “GB6722-2014”.

Fig. 6The relationship between the single explosive charge and the maximum vertical vibration velocity of the pipe

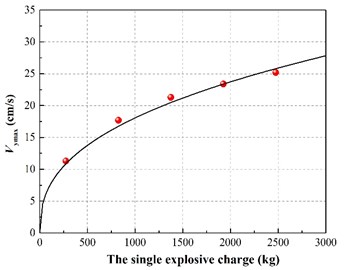
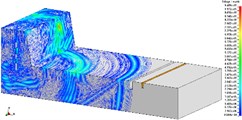
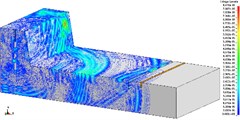
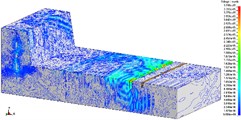
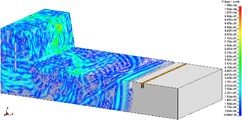
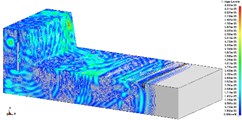
In order to research the relationship between the depth of vibration-isolating slot and the vibration-isolating effect, under the condition that vibration-isolating slot is 3.0 m deep, the vibration velocity distribution map is shown in Fig. 7 and Fig. 8. The number of holes for a single explosive charge is only 1 hole or 9 holes which are represented here, and the other is no longer described. Taking 275 kg and 2475 kg homogeneous explosive charge respectively, the comparison of vibration waveform between the extracted pipeline with 3.0 m vibration-isolating slot and that without vibration-isolating slot has been shown in Fig. 9.

Fig. 7Isolation effect of vibration-isolating slot on blasting seismic wave propagation (275 kg charge per delayed interval, 3.0 m depth)

a)

b)

c)

Fig. 8Isolation effect of vibration-isolating slot on blasting seismic wave propagation (2475 kg charge per delayed interval, 3.0 m depth)

a)

b)

c)

Fig. 9The clipping effect of vibration-isolating slot on the blasting seismic wave

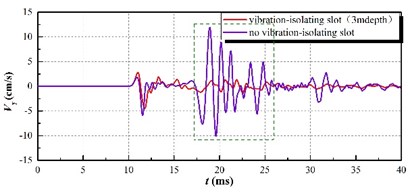
a) 275 kg charge per delayed interval

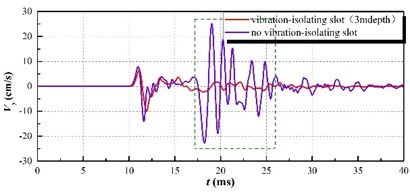
b) 2475 kg charge per delayed interval

According to the diagram, it is implied in the vertical vibration speed history curve that the vibration speed of the pipeline with vibration-isolating slot has a larger decrease than that without slot as a whole. In particular, the vibration curve of the dotted line in the figure shows that the vibration isolating effect of vibration-isolating slot on the shock wave is obvious. In order to analyze the influence rule of the vibration-isolating slot depth on the vibration-isolating effect, it extracts and computes the numerical results of the other slots, and calculates the vibration-isolating ratio.

Based on the above numerical results, the peak velocity $V_{ymax}$ and the vibration-isolating ratio $\lambda$ of the vertical vibration in various working conditions were discussed. The calculation results show that, whether it is 275 kg homogeneous explosive charge or 2475 kg homogeneous explosive charge, the vibration-isolating rate of the vibration-isolating slot increases along with the increase of the depth of the vibration-isolating slot, which is consistent with the research results.

Fig. 10The vibration-isolating ratio λ with the depth of different vibration-isolating slot

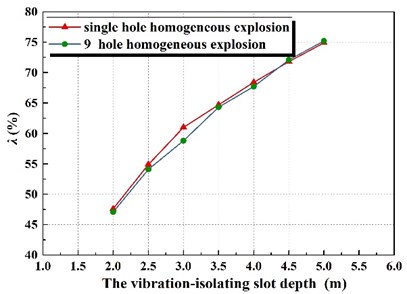
a)

b)

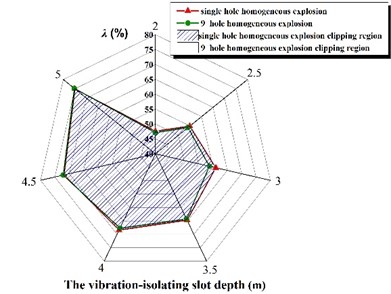
Fig. 11The vibration-isolating ratio λ with the depth of different vibration-isolating slot

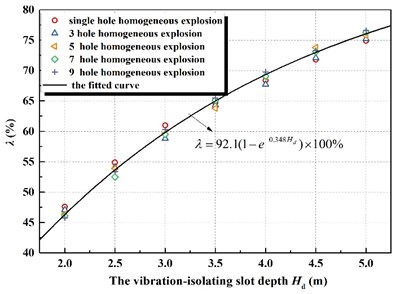
In addition, we found a valuable rule: two kinds of homogeneous explosive charge in different working conditions are different, but the vibration-isolating ratio is very close in vibration-isolating slot with same depth $H_d$. The calculation data based on 275 kg homogeneous explosive charge (1 hole homogeneous explosion), 1375 kg homogeneous explosive charge (5 hole homogeneous explosion) and 2475 kg homogeneous explosive charge (9 hole homogeneous explosion) has been shown in Fig. 11.

It can be seen from the above diagram that the amount of homogeneous explosive charge (homogeneous detonating holes) in several working conditions is different, but the vibration-isolating ratio is quite close if vibration-isolating slot structure parameter, the depth $H_d$, is same, which should be the essence of physical mechanics phenomenon. Considering the practicability in engineering applications and the convenience to formulate norms for relevant departments, fit the data and the fitting formula expresses as the followed:

where vibration-isolating ratio is $\lambda$, depth of vibration-isolating slot is $H_d$, $e$ is 2.718.

4. Conclusions

1) Nonlinear dynamic finite element analysis model can well simulate dynamic response of the geotechnical field subjected to millisecond blasting. Simple and practical, the numerical method can be selected and adjusted according to different research objectives and content, which will provide technical support for the research on the influence of millisecond blasting on the vibration-isolating effect of vibration-isolating slot.

2) The vibration speed of the pipeline with vibration-isolating slot has a larger decrease than that without slot as a whole. The homogeneous explosive charge in different working conditions are different, but the vibration-isolating ratio is very close in the vibration-isolating slot with same structure parameter. The millisecond blasting is hardly affected by total explosive charge. But the blasting seismic intensity is influenced by explosive charge in each stage directly.