Numerical investigation for influence of pre-twist on stress behavioral characteristics of curved blade

1. Introduction

The application of pre-twisted blades in the recent decades have pulled a lot of consideration particularly for marine propulsion, tilt rotors, wind turbine blades and helicopter applications. From a basic perspective and structural point of view the effect of pre-twist not only influences on the torsional property but also on the bending rigidity. In addition to the pre-twist establishes a coupling between torsion and extension for isotropic materials also. Additionally, for composite materials a coupling exists between bending and shear. The manufacturing of the blade involves various parameters which are of complicated nature there by making the boundary conditions more complex which results in solving the structural analysis more cumber some process. Consequently, for these complicated geometries theoretical approaches of classical beam or plate theory are used for solving the problem. To find out the simulation results finite elements of either beam, plate or shell elements are used for pre-twisted blades. An extensive research regarding static, dynamic analysis was carried out by Rosen [1] for pre-twisted beams. For a refined structural analysis of pre-twisted blades he suggested an appropriate treatment of section warping’s should be done. From his perception, in the structural response of composite blades bending and torsion warping will play a significant role and should be taken directly into consideration. Mansfield [2] built up an adaptability formulation for thin walled composite beams made of two cell cylindrical tube section. Most of these researchers have used FEM as a basic tool for carrying out the analysis. Taylor [3] used elementary beam theory for an aero foil cross section which are of asymmetric in nature and are pre-twisted along its length. He treated pre-twisted blade as a cantilever beam fixed rigidly to the hub. For such cylindrical blade sections the stresses acting on the blade are determined taken from a neutral axis parallel to the nose tail (pitch) line of the expanded section. The applicational use of cantilever beam theories have yielded reasonable results for stress estimates at selected points of straight narrow blades and wider blade propellers whose width to length ratio is about one. Modified form of beam theories are proposed. The application of shell theory for blade analysis was first proposed by Cohen [4] who considered a simplified propeller blade model as a helicoidal shell having variable thickness and infinite width (however when this approach was applied to the problem of a shell containing finite width solution became impossible due to un satisfaction of boundary conditions). Barbero [5] used a simple formulation based on Timoshenko’s beam theory to determine the bending and shear stiffness of thin walled composite beams with open and closed cross sections subjected to bending and axial loads. The formulation was further carried out by Massa and Barbero [6] to compute torque and shear stiffness. Both these papers considered the effect of flexural torsional coupling and shear flexibility caused due to the bending of the structure. Chopra et al [7] carried out an experimental work along with analytical model over Graphite epoxy composite beams exhibiting bending torsion, bending-shear coupling, extension-torsion for a typical helicopter rotor blades [8, 9]. Based on Ritz method, Kosmata [10] developed an analytical model which takes into account of extension-bending-torsion coupling effects of initially twisted beam having irregular cross section. White and Bendiksen [11] studied the aero elastic behaviour of titanium and composite flat blades having low aspect ratio, they used Rayleigh’s Ritz formulation as the basis for their studies. A nine noded shell element was used by Oday I. Abdullah [12] to compute the dynamic behaviour of a damaged rotating blade. In his study the effect of initial twist and rotational effects excluding corollis component of acceleration are taken into consideration. Kumar and Palaninathan [13] used degenerated shell element for studying the finite element analysis of a laminated shells. A ten noded triangular shell element having 30 degrees of freedom was used by Khader Naim [14] to determine the static analysis of pre-twisted and cambered fan blades.

2. Material and methods

The main objective of the present research work emphasizes on the study of stress behavioral characteristics of the curved blade tested with both conventional and composite materials. Application of composite materials are more suitable than isotropic materials, which is mainly due to the high strength to weight ratio. The following Tables 1 and 2 gives the cross-section details and material properties of conventional and composite material used for curved blade analysis.

3. Results and discussions

In this present study the effect of pre-twist, fiber orientations and layer lamination on the stress analysis of a twisted blade are considered. In order to find out the stress behaviour response for the blade, shell 181 elements are used for finite element modelling and the results are varied in steps of twist angles from 0 to 90°. The corresponding tables shows the quantative comparisons of the various stresses and deflections of a non- rotating blade. The blade is meshed up with shell elements using Hypermesh solver and the numerical results are obtained using ANSYS. The Table 3, 4 shows the Stress values of Titanium and composite curved blade for various pre-twist angles and the corresponding graphs 2a, 2b represents the stress values as a function of pre-twist angles. The Table 5 shows the variation in stresses of a pre-twisted composite blade drawn with varying number of layers at an angle of 18°. Finally, Table 6 shows the results for inter laminar stresses of composite blades with various pre-twist angles and number of layers.

Fig. 1Pre-twisted single blade with pressure distribution

Fig. 2Stress values comparison for various pre-twist angles for isotropic and composite material

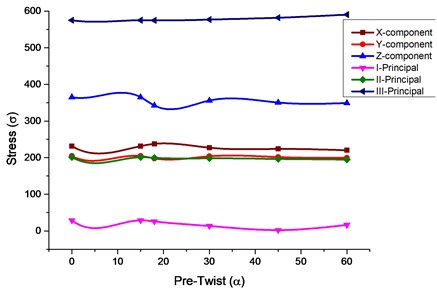
a) Isotropic

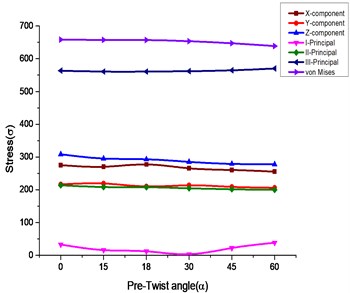
b) Composite

Fig. 4Stress value comparison for varying layers

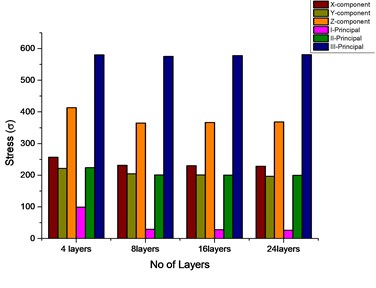
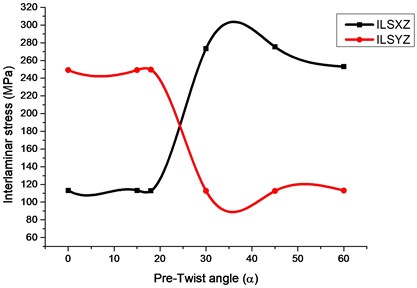
Fig. 5Inter laminar stress comparison for various pre-twist

4. Conclusions

In this study the solid model of the curved blade is developed using CATIA, the finite element modelling is carried out using Hyper mesh and the analysis results are interpreted by using FEA based simulation software ANSYS 15, subjected under clamped-free conditions. The blade was modelled as a cantilever oriented arbitrarily with respect to the rotating axes. The effects of initial twist, fiber orientation, and composite laminates were investigated for finding out the deflection, Principal stresses, von Misses stress XYZ component stress and corresponding inter laminar stresses are determined and corresponding graphs are plotted. Finally, a comparison has been made between isotropic and composite. From the results, it can be predicted by proper tailoring composite materials at specified ply angles and varying the number of layers stresses and deflections can be enhanced to cope up with isotropic materials.

1. From Table 3 it shows that the XYZ component of stress for an isotropic titanium curved blade lies maximum for a pre-twist angle between 0 to 30°.The principal component of stresses first and third principal stress are maximum at pre-twist angle of 60°.The second principal stress and von Mises stress are maximum for pre-twist angle of 0°.

2. From Table 4 the XYZ and principal component of stress (First and Second) for a composite curved blade lies maximum for a pre-twist angle of 0°. The third principal component of stress is maximum at pre-twist angle of 60°.

3. From Table 5, 6 it shows that with increasing number of layers from 4 to 24 a reduction in stress values are obtained for both principal component and inter laminar stresses and are depicted in Figure 4. With varying pre-twist angles from 0 to 60° in Figure 5 an incremental growth of inter-laminar stress along XZ axis and reduction along YZ axis can be observed.