Study on seismic behavior of a concrete elevated tank with frame shaped base using SMA damper

1. Introduction

Water tanks are considered as the main members of the water supply networks for maintaining, storing and providing the required water pressure. So, it is essential for water tanks to have a proper shape, absorption capacity and capability of depreciating the earthquake energy, moreover, their stability should be considered in designation stage. According to the recent earthquakes, elevated tanks are regarded as the most vulnerable structures and it is essential to accomplish a more precise research and study on the structure behavior, which may be subjected to the seismic conditions. The tank and base of an elevated tank are made of concrete, and the shape of the tank may be either conical or cylindrical, while the tank base may be a moment frame or a shaft frame. A base made of a reinforced concrete frame has the capability of reflecting the force during the other nodes yielding, due to the great degree of undetermined and various paths of load transmission. Hence, their seismic behavior is desirable. During the designation of base, the formation of any joints at the column should be avoided, since the formation of the joints on the columns, causes an increase in joint count and the occurrence of non-linear deformations and damages in the structure are indispensable.

In what follows, some of the major studies on the elevated liquid tanks are presented. Haroun and Ellaithy [1] developed a model including analysis of a variety of elevated rigid tanks exposed to shifting and rotation. Haroun and Temraz [2] analyzed two-dimensional x-braced elevated tanks supported on the isolated footings to investigate the impact of dynamic interaction between the tower and the supporting soil-foundation system but they neglected the sloshing effects. Dutta [3] purposed the alternate tank staging configurations for reduced torsional vulnerabilities. Livaoglu and Dogangun [4] suggested a simple analytical procedure for seismic analysis of fluid-elevated tank-foundation-soil systems, and they used this approximation in selected tanks. Livaoglu and Dogangun [5] studied the impact of foundation embedment on the seismic behaviour of elevated tanks considering fluid-structure-soil interaction. Moslemi et al employed the finite element technique to investigate the seismic response of liquid-filled tanks. The free vibration analyses in addition to transient analysis using modal superposition technique were carried out to investigate the fluid–structure interaction problem in elevated water tanks [6]. The seismic response of both concrete and steel tanks has been extensively investigated by means of experimental and numerical methods. Such studies date back to as early as the 1940s and later by works of Housner [7] and other researchers such as Kianoush and Ghaemmaghami [8], Moslemi and Kianoush [9].

A shape-memory alloy is known as a smart material which has peculiar characteristics and it can be used in order to reduce the earthquake damages on the structures. It also overcomes the mentioned limitation of the system by limiting the transmitted displacement (Seismic Isolation techniques) or by absorbing the energy of the seismic event (Energy Dissipation techniques). One energy dissipation technique consists of using dampers based on Shape Memory Alloy (SMA) wires. Shape memory alloys have many interesting properties that can be exploited in these applications, namely their superelasticity, high fatigue resistance, near strain-rate independence (in certain conditions related to temperature control), among others (Dolce and Cardone (2001)) [10]. Fig. 1 represents a generic stress-strain tensile curve of a superelastic SMA material, for the case where the SMA is above its austenitic phase transformation temperature ($Af$ in the literature), i.e. the SMA material is in the austenitic phase at room temperature. This metallurgical state provides better properties for this type of dampening application (Dolce et al. (2000)) [11]. During the recent years, scholars have studied the feasibility and capability of using SMA in the fields of structure and earthquake engineering. In 1991, for the first time Graesser and Cozzarelli conducted a research focusing on the utilization of Nitinol as an earthquake damper. They investigated the impact of frequency and loading history on the amount of energy depreciation of the Nitinol wires [12]. In 2006, Chun et al. presented novel seismic isolators by utilizing the SMA in order to overcome the insufficiencies of the lead-core isolators. They screwed the SMA wires in longitudinal direction, around the elastomeric support sections and they developed web wires by exploiting the attenuation and ultra-reactionary properties of the SMA material. First, they equipped a three-span continuous steel covering bridge with these isolators, then a comparison was made between the equipped bridge and a bridge with lead isolators. Chun et al. proved that the plastic SMA isolators limit the relative displacement of base and deck, especially during the sever stimulus. That is, although these kinds of isolators increase the bases' seismic demands, but due to the ultra-reactionary property of the SMA materials, there will be no permanent deformation in the structure. So, the instability and the need for an isolator replacement after the earthquake are not expected. In 2006, Saiidi and Wang [13] presented a reinforced concrete column with SMA rebar. They planned to resolve the issue of permanent deformations linked to the steel rebar of the common concrete columns. They studied the seismic performance of the proposed columns by accomplishing an analytic-experimental research. Andrawes et al. [14] presented a novel seismic optimization method for reinforced concrete columns of the bridges. They utilized a wrapping screw made of Martensitic SMA in order to develop a kind of active confinement for columns via pre-stressing and heating. They initially applied a uniaxial compression test on the columns confined by SMA screws, and found that concrete resistance and ductility were significantly increased, even under a low confinement pressure. They utilized the experiment results in order to calibrate the analytic model of a column with SMA screws. The main objective of this paper is to propose a method for reducing the displacement of elevated tank. Due to the fact that SMA material possesses a series of characteristics like high attenuation capacity, durability and resistance against fatigue and corrosion etc., SMA can be employed and adopted in different scientific and industrial fields. However, different designation ideas are presented and compared with each other in order to maximize the ideal effect of suggested dampers on tanks. The analysis of behavior of the reinforced tanks with suggested SMA manifested that this system is able to minimize the structure damages and post-earthquake deformations.

Fig. 1Generic stress-strain response of a SMA above temperature Af [11]

2. Geometric and mechanical characteristics of models

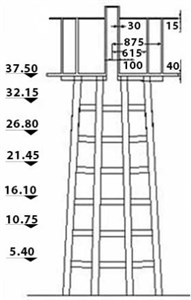
The utilized elevated concrete tank consists of a tank with water capacity of 1500 m³, which is standing on a frame-shaped base with 8 columns with dimensions of 1.2×1.2 on the seventh floor (with a moment frame system) and height of 37.5 m above the foundation, to beneath of the tank. It is designed and loaded with regard to the ASCE7-05 code for areas with the highest risk zone and soft clay [15]. For reducing the hydrodynamic forces of water to the wall of this reservoir and for increasing the efficiency, the tank was divided into two sections of 750 m³. The non-linear static analysis was applied on the base of the tank considering the ASCE7-05 standard by Abaqus V10.06, and the obtained results were studied. For modelling the tank, the shell elements were utilized. In the developed model, the walls and bottom of the tank were modelled using S8R element. This element is an eight-node shell element which possesses reduced integration points. With regard to the fact that the present article aims at investigating the behavior of tank's base, so the reinforcements of the tank’s wall were not considered, and the associated properties of the materials were assumed to be elastic. Hence, the elements of this region do not enter into the plastic and a nonlinear behavior zone. Each wall has 90 elements and the bottom and column of the tank were modelled using 108 elements, so totally 486 elements were defined in the tank model. Fig. 2. presents the geometric properties of the elevated water tank.

The Housner’s model has been adopted in fluid modeling, since the existence of internal wall prevents the water turbulence to a great extent and it confines the water freedom. According to this method, the water mass is divided into convective and impulsive masses. There is a rigid connection between impulsive water mass ($M_0$) and tank wall, in the height ($h_0$) from the tank bottom. The convective water mass $M_1$ is connected to the wall via a coil with stiffness of $k_c$, in the height of $h_1$ and it drifts with a lower period, compared to the impulsive zone.

The governing equations of the models and the values of convective and impulsive mass for both sections are presented in Table 1. In the external region of the tank, the length at which water wave is capable of fluctuating, is extremely less than the external diameter of the tank which is due to the internal wall. Hence, in the calculations, the greatest freedom length at which water is able to fluctuate, is considered as the radius of the tank (Fig. 3).

Fig. 2Elevated water tanks

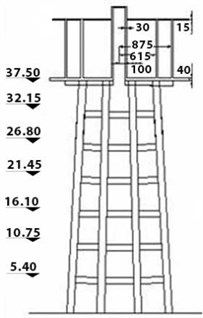
a) Vertical cross section of the reinforced concrete elevated tanks

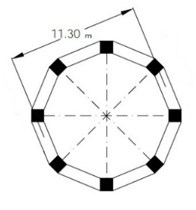
b) Arrangement of the columns and beam on the first storey

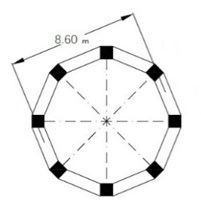
c) Arrangement of the columns and beams under the tank container

Fig. 3Housner’s mass-spring model [7]

With regard to the fact that the water convective mass moves along with walls and bottom of the tank, this mass will be added to the walls. To this end, the tank wall was modeled with height of 2$h_i$ and density of equaling to concrete and half of the impulsive mass of the tank. In Housner’s model, the sum of the impulsive and convective masses is less than the water total mass existing in the tank. This mass has been compensated by increasing the bottom density. The convective mass of water with a height of $h_1$ from the tank bottom is connected to the tank internal wall in a centralized manner, using four coils with total stiffness of $K_c$. Due to the fact that each of two sections of the tank has a convective mass and both of them are located at the same height, both of the masses are modeled in the same height, but with 10 cm off-center from the tank center. Fig. 4 presents the sections of tank tolerating the impulsive and convective masses.

Fig. 4Software model of tank

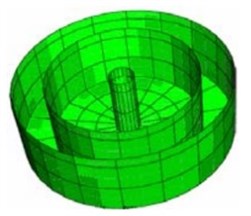
a) Tank section which tolerates the impulsive mass

b) Modeled impulsive mass

c) Free length of the fluid fluctuation in the external region

Moreover, in the meshing of the moment frame base, we have used the FRAME element during the modeling. This is a two-node element with plasticization potentiality at its two end points (Fig. 5).

Fig. 52-node frame element

Fig. 6 displays elevation view of an SMA-rubber bearing. The SMA-rubber bearing (SRB) used in this study has the same elastomeric bearing (EB) with 457 mm×305 mm×152 mm ($L$×$W$×$H$) Fig. 6 [16]. The reinforced concrete columns of the first and seventh floors are made of SMA rebar with thickness of 30 mm and length of 5.35 m, with frame-shaped base. This model is based on an experimental work on the available reinforced columns of the reference [15]. The utilized SMA in these specimens is made of ultra-reactionary or super elastic NiTi (Nickel-Titanium), which is known as Nitinol. Table 3 presents the mechanical properties of the SMA used in this study. As the shaped memory alloys are not defined in the Abaqus Software, the properties of SMA were incorporated into the software via another application by coding in a programming tool [17].

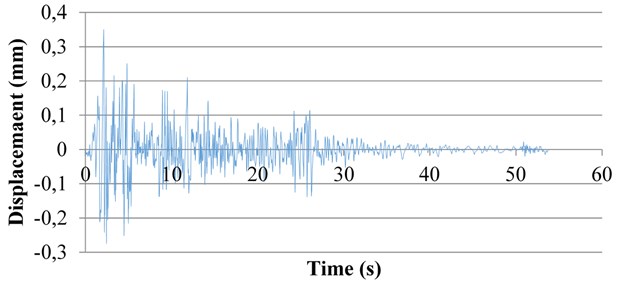
The present experiment applied the simulation of ground movement in the form El-Centro earthquake by a shaking table. Fig. 7 presents the acceleration-time diagram of the El-Centro earthquake. The earthquake record was applied using the models developed by Abaqus and the structure was analyzed using the non-linear static analysis method. Fig. 6 illustrates the method of applying accelerogram of El-Centro earthquake in the software environment.

Fig. 6SMA-rubber bearing and its deformation: elevation view of an SMA-rubber bearing [16]

Fig. 7Diagram of El-Centro earthquake record

In this paper, five specimens of tank with a frame-shaped base made of SMA damper were modelled in Abaqus software. Fig. 8 depicts the schematic figure of five models. The location of SMA damper is highlighted by red lines.

M1: Concrete elevated tank with frame shaped base, without SMA damper;

M2: Effect of single-string SMA of the damper on the upper section of frame-shaped base of tank;

M3: Effect of double-string SMA of the damper on the upper section of frame-shaped base of tank;

M4: SMA effect on the first-floor rebar of the tank frame-shaped base;

M5: SMA effect on the seventh-floor rebar of the tank frame-shaped base.

Fig. 8Modelling of elevated tanks

c) M3

b) M2

a) M1

e) M5

d) M4

3. Model validation

The properties of the sample, designation assumptions and tank analysis were modelled with regard to the information of reference [15], using Abaqus software. The obtained results indicate the desirable accuracy of M3. Fig. 8(a) displays the Abaqus model and Fig. 9(b) presents a comparison made between the base-shear-displacement diagrams of software models and reference information [15]. Comparing these diagrams reveals that there is a difference less than 0.5 between the accomplished model and reference [15], which is acceptable in numerical studies. This mount of error is due to the difference between the element count and non-linear characteristic of materials.

Fig. 9a) M1 model for comparing the shear base-displacement diagrams with that of reference [15], b) modelling of elevated tank

a)

b)

4. Numerical study on obtained displacement curve of the models

4.1. Sample 1: Elevated concrete tank with frame-shaped base, without SMA damper

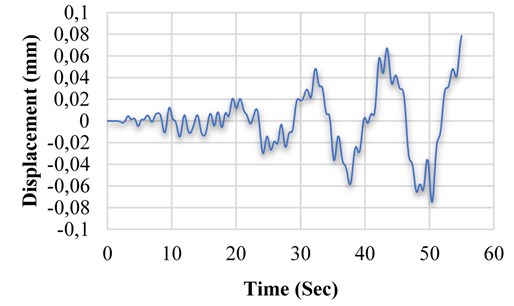
M1 is an elevated tank with a moment frame and it includes 100 % water. This model does not have an SMA damper. Fig. 10 presents the displacement curve of M1 model.

Fig. 10Displacement variation of M1 model in terms of time

4.2. Sample 2: Effect of single-string SMA of damper, on the upper section of tank’s frame-shaped base

M2 model represents the placement of the SMA in a single-string manner around the damper, in the upper section of the structure. (Location of tank to framed-shaped base connection). Fig. 11(a) illustrates the mentioned model. The sections that are specified by red colour refer to the placement location of the SMA damper.

Fig. 11Modelling of elevated tank

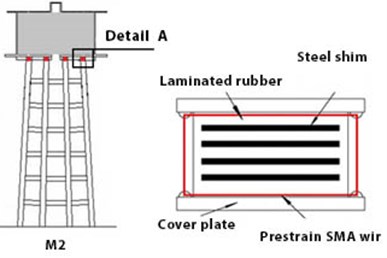
a) M2 model

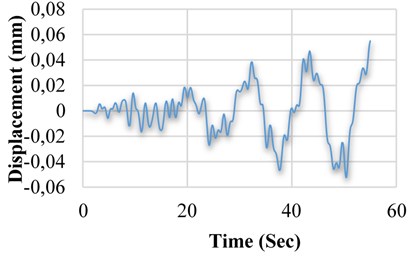
b) Displacement variation of M2 model in terms of time

c) Plastic strain of the M2 model

4.3. Sample 3: effect of double-string SMA of damper on the upper section of tank’s frame-shaped base

Model M3 represents the placement of the SMA in a double-string manner around the damper, in the upper section of the structure. (Location of tank to framed-shaped base connection). Fig. 12(a) illustrates the mentioned model. The sections that are specified by red colour refer to the placement location of the SMA damper.

Fig. 12Elevated tank modelling

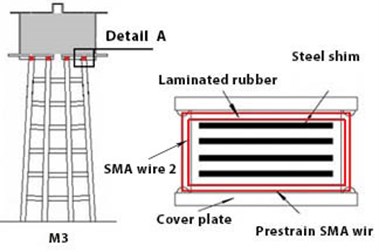
a) M3 model

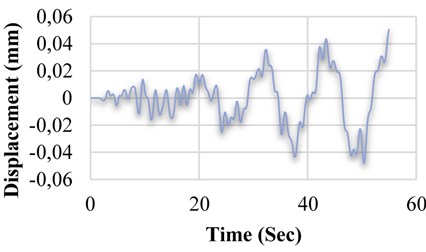
b) Displacement variation of M3 model in terms of time M3 model

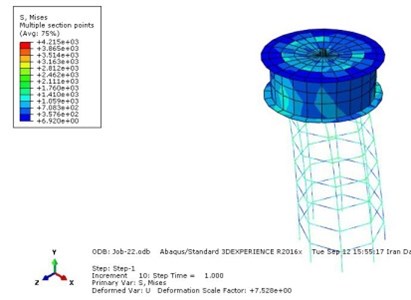
c) Plastic strain of M3 model

4.5. Sample 5: Effect of SMA on the rebar of seventh-floor of tank frame-shaped base

Model M5 demonstrates the placement of intelligent materials on all available fittings of the eight frame-shaped bases in the seventh-floor (with length of 5.4 m, within the frame first-storey). The areas which are highlighted using red color refer to the placement location of SMA material (Fig. 14).

Fig. 13Elevated tank modelling

a) Model M4

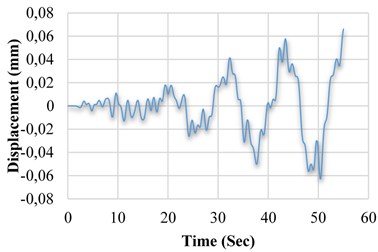
b) Displacement variation of M4 model in terms of time

c) Plastic strain of M4 model

Fig. 14Modelling of elevated tank

a) Model M5

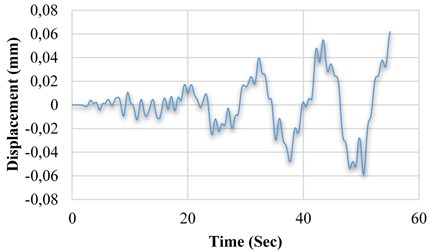
b) Displacement variation of M5 model in terms of time

c) Plastic strain of M5 model

4.6. Comparison between obtained results from models analysis

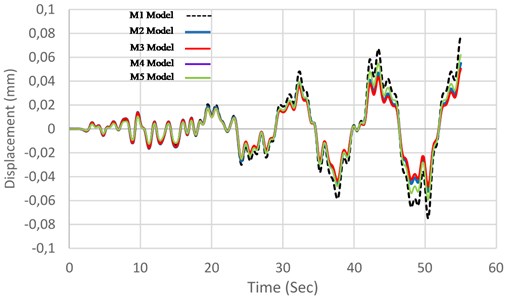
Fig. 15 through 14 show the comparison made between the displacement diagrams of software models linked to a tank with frame-shaped base. After applying the earthquake record on the five models, including M1, M2, M3, M4 and M5 and performing the time history analysis, it became evident that the M3 model has a relatively less displacement (about 35 percent), compared to the tank without SMA (M1 model). In addition, compared to the three models having SMA damper, in M2 model, we observed 30 percent less displacement by placing a single-string of SMA around the damper, compared to the M1 model (without SMA). In M4 and M5 models, applying SMA alloys on the rebar of the first and seventh floor, decreased the displacement rate to 16 and 21 percent in the tank with frame-shaped base, compared to the M1 model.

Table 4Comparison of maximum displacement variation of models

Model name	Maximum displacement (cm)	Amount of displacement reduction (percent)
M1	0.0078	–
M2	0.0055	30
M3	0.0050	35.82
M4	0.0066	16
M5	0.0061	21

Fig. 15Comparison between displacement variation of the models in terms of time

5. Conclusions

In this research, we endeavored to investigate and analysis the samples of an elevated tank with frame-shaped bases using SMA damper. Then, in the above-mentioned models, the force-displacement diagram and relative displacement of the models, were scrutinized by applying the different combinations of SMA alloys on the tanks with a same capacity and height. Our findings are as follows:

1) M2 model with a single-string of SAM alloy around the damper, presents 30 percent less displacement than a tank without SMA (M1). Moreover, in the M3 model with double-string SMA around the damper, the reduction trend of displacement was improved about 5 percent, compared to M2 model.

2) M2 and M3 models exhibited larger ductility than M4 and M5 models, which is mainly due to the placing of the SMA at the location of tank to base connection. As a result, the utilization of these dampers is suggested, especially in high seismic areas.

3) With regard to the M4 and M5 models with highest amount of SMA use in the number and length of the floors related to the frame-shaped bases, it can be deduced that the employment of this material in that part of the structure is not economical.