Centrifuge experiment and numerical study on the dynamic response of air-backed plate to underwater explosion

2.1. Shock wave

During an underwater explosion, there are two main shock loadings, shock wave and bubble pulse. The shock energy delivering to the structure by the underwater explosion is closely related to the charge weight and standoff distance. On the shock wave, Cole had made lots of experimental researches. By analyzing the pressure-time cures of the specific test point, he put forward the empirical formula of UNEDX shock wave based on the similarity theory. The shock pressure at a given point has a sharp peak in time, followed by a decaying exponential function, which can be given by [20]:

And the function of peak pressure $P_m$ (MPa), and the time decay constant $\theta$ (μs) are:

where, $P\left(t\right)$ is the pressure (MPa) at any instantaneous $t$ (μs), $W$ is the charge weight (kg), $R$ is the standoff distance (m), $R_0$ isthe shortest radial distance, $t_d=(R-R_0)/c_w$is the time delay (μs), $c_w$ is the sound velocity in water (m/s), and $k_1$, $k_2$, ${\alpha }_1$ and ${\alpha }_2$ are the shock wave parameters of the explosive.

2.2. Bubble pulse

On the periodic motion of bubble pulse, the approximate relation of the emergence time of the first of bubble pulse $T$ (ms) and the maximum bubble radius $r_{\mathrm{m}\mathrm{a}\mathrm{x}}$ (cm) are given by Cole as follows [20]:

where $D$ is the water depth (m) of the explosive, $D_0$ is of equivalent water depth (m) of atmospheric pressure, which is about 10.33 m, and $k_3$ and $k_4$ are the motion parameters of the bubble.

Moreover, based on the assumption of linear compressible fluid, Geer and Hunter [21] derived the equations of motion of UNDEX bubble, through doubly asymptotic approximation technique (DAA), which simultaneously considers both dilation and translation during bubble oscillation. And the bubble motion can be expressed as:

where ${\rho }_g$ and $c_g$ respectively represent density and corresponding sound velocity of inner gas product, $\zeta$ is the impedance of inner gas and outer fluid, $P_I$ is the hydrostatic pressure, which includes the atmospheric pressure, $P_g$ is the gas product pressure, $C_D$ is the empirical flow drag parameter, and $E_D$ is the correction coefficient to match the experiment result. By giving the initial condition, the five characteristic parameters of bubble oscillation, namely, bubble radius $a$, floating upward displacement $u$, expansion velocity potential ${\phi }_{l0}$, translational potential ${\phi }_{l1}$ of outer fluid and translational potential ${\phi }_{g1}$ of gas product, can be calculated with Runge-Kutta method.

And the free-field pressure during the bubble oscillation phase can be expressed as [22]:

where $\ddot{V}\left(t\right)$ and $\ddot{a}$ are the second derivative of bubble volume and radius versus time, respectively.

3.1. Experiment setup

In this work, the experiments were performed on LXJ-4-450 centrifuge in IWHR laboratory, which has a maximal acceleration of 300 G, effective load of 1.5 t and maximal turning radius of 5.03 m. As Fig. 1 shown, the model box (1.2 m×0.7 m×0.9 m) was put in the basket (1.5 m×1.0 m×1.5 m) and excited centrifugal force $NG$ along the cantilever direction. The model box was made with alloy plates fastened by bolts, and there was a glass observation window at one of side of the box. The inner walls of the box were coated with absorption materials to reduce the wave reflection. As indicated in Fig. 3, the steel plate of size 0.7 m×0.6 m×0.05 m with an exposed area of 0.6 m×0.65 mwas fastened by cement mortar with thickness of 5 cm at the right, left and bottom side. A3 steel was selected as the target plate and the water-storage depth in the model box was 0.6 m.

Fig. 1The centrifuge

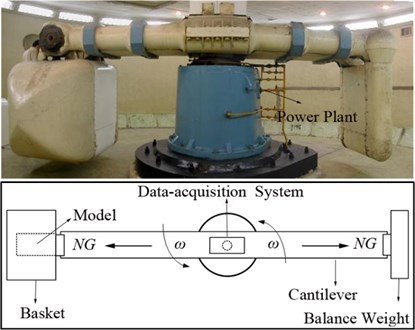
Fig. 2Micro detonators and RDX spherical explosives [18]

The explosives or micro detonators and the pressure sensor (ICP138) were located along the perpendicular line though the symmetry axis of the plate and at a same water depth. There was a high-speed camera (FASTCAM-ultima APX) with a frequency of 2000 fps and resolution of 1024×1024 put near the observation window to shoot the bubble pulse. The accelerometers (ICPM350B01) and strain gauges (TSJ120-4AA) were installed at the back of the plate (Fig. 4). All the dynamic signals were collected through data-acquisition system with 32 channels, which was put on the top of the shaft of centrifuge. The data-acquisition system was set delay trigger up to 20 ms to ensure obtain the complete measured data containing the initiating time of the charge. The sampling rate was set to 1 MHz, and the strain amplifier adopted 1/4 bridge circuit.

Fig. 3Schematic diagram of setting in model box (mm) [18]

Fig. 4Schematic diagram of sensors setting (mm) [18]

3.2. Explosives

In order to ensure precision in small quantity, RDX spherical explosives and micro detonators were used in the experiments (Fig. 2). The RDX spherical explosives are composed by two separated hemispherical explosives, and a 10 cm long detonating fuse with a diameter of 2.6 mm and equivalent TNT weight of 48 mg/m, was detonated by a micro detonator (RDX equivalent 50 mg) to guarantee the reliable central initiation of the charge. Thin plastic sleeve made by 3D printing, hot pyrocondensation (HP) pipe and hydrophobic membrane were adapted to tightly connect and protect the whole detonation device. The density of explosive is 1.65 g/cm³, the detonation heat is 5200 J/g, and the detonation velocity is 8160 m/s. Three micro detonators were bounded together to simulate the effect of 150 mg detonator in this work. The explosive is converted to TNT equivalent by a coefficient of 1.58.

3.3. Determining shock parameters of shock wave

Seventeen tests, using different amounts of RDX charges and detonators, were performed in this work. The experimental conditions are shown in Table 1, and $W$, $CF$, $D$, $L$ and $R$ separately represent charge weight, centrifugal force, water depth, test distance between the charge and the plate, and standoff distance between the charge and the pressure sensor. Since some errors may occur during experiments due to underwater currents and irregular tension from the signal cables , all the effective standoff distances in each case were modified by the multiplication of the wave-propagating velocity (1498 m/s, 25℃) [21] .The Fig. 5 shows some of the time-history of pressures measured, from which it can be found that the peak pressure increases with the decrease of $R$, and although there is some difference between the peak of S1 and S4 owing to the charge weight or test error, it can also prove that the centrifugal force have no effect on the shock wave, which can be also indicated in Table1. The reason is that the shock wave phase is too short, so the centrifugal (or gravity) effect can be ignored, and in addition, the peak pressure of S6 and S7 illustrate that the small change in water depth almost have no influence on the shock wave test of this work, so, the shock wave parameters can still be dealt with Eqs. (1) to Eqs. (3).

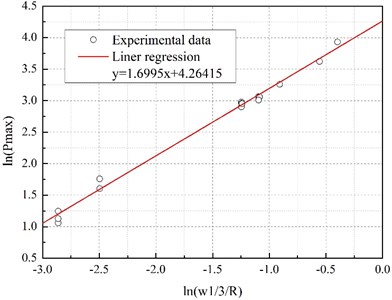
The relationship between peak pressure $P_m$ and weight-distance parameter $W^{1/3}/R$ can be determined through a bi-logarithm linear regression [23], and the regressive curve is $y=$ 1.6695$x+$ 4.26415, where, $x=\mathrm{l}\mathrm{n}\left(\mathrm{P}\right)$ and $y=\mathrm{l}\mathrm{n}(W^{1/3}/R)$. Fig. 6 shows the experimental data and regression curve. The peak pressure can be calculated by taking exponential of the curve, and the time decay constant can be obtained through a bi-logarithm linear regression on each pressure time-history curve. According to Eqs. (2) and (3), the peak pressure $P_m$ and time decay constant $\theta$ are given as:

Fig. 5Pressure-time curves under different working conditions

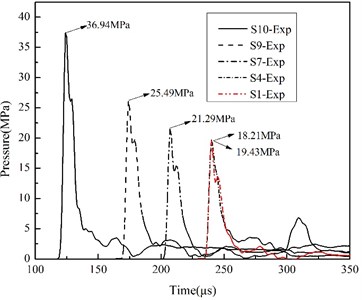
Fig. 6Relationship between peak pressure and weight-distance parameter of charge

3.4. Centrifugal effect on bubble pulse

Before every test, a scale was put at the same position of the charge and shoot by the high-speed camera. Many data points of every bubble image were depicted according to the scale to get the mean radius of the bubble at a given time, and since the detonation process is very short when compared with the bubble oscillation, the moment of the emergence of the highlight area for the first time was approximately regarded as the beginning time of the bubble oscillation.

Owing to the centrifugal force generated by the high-speed rotation of centrifuge, the gravitational field of fluid and bubble buoyancy change a lot. According to empirical Eq. (4) and (5), the motion parameters $T$ and $r_{\mathrm{m}\mathrm{a}\mathrm{x}}$ of bubble are only related to the water depth $D$ when the charge type and weight is determined. In this work, different centrifugal force $NG$ were converted to water depth $D$ based on the equivalent conversion of hydrostatic pressure, and with the test data of bubble, the emergence time of the first of bubble pulse $T$ and the maximum bubble radius $r_{\mathrm{m}\mathrm{a}\mathrm{x}}$ are fitted as follows:

From Eqs. (12) and (13), and the bubble motion image (Fig. 9), it can be directly seen that $T$ and $r_{\mathrm{m}\mathrm{a}\mathrm{x}}$ decrease with the increase of centrifugal force. And in order to explain this phenomenon in centrifugal model experiment, the radius-time and pressure-time curve of bubble are calculated through Eq. (6) to Eq. (9). Fig. 7 and Fig. 8 shows the comparison of Geer and Hunter model and experimental data.

Fig. 7History of bubble radius

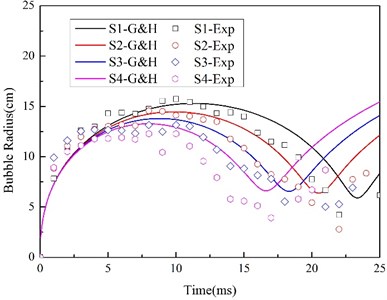
Fig. 8Pressure-time curves of bubble loadings [18]

Fig. 9Bubble motion under different centrifugal forces

a) S2, $CF=$ 30 G

b) S5, $CF=$ 50 G

It can be seen that the change trend of the measured and the theoretically calculated bubble motion are compared well, and peak bubble loadings decline when centrifugal force rising, ignoring the initial charge weight difference. In addition, the theoretical loading curves are more symmetric as a result of assumption of symmetric bubble in Geer and Hunter model. Zamyshlyayev [24] also established a shock loading model dividing the whole explosive process into five phases. On the basis of Zam’s theory, the hydrostatic pressure higher, the peak bubble loading higher, which seems to be opposite to our result. And it is because of the assumption of still bubble in the first motion cycle in his model. However, when the centrifugal force increases more, the bubble oscillation become more obvious with the expansion and translational potential changing more sharply, so, the whole bubble displacement in vertical direction increase a lot, and the first bubble motion cycle shorten for the increasing drag force, which can be calculated by the Geer and Hunter model. In each case of this work, the pressure sensor was set up at a specific position, but the bubble center is a moving point source and the distance from the bubble center to the sensor lengthen with the rising centrifugal force, so, although the increase of initial hydrostatic pressure raises the bubble potential energy when bubble shrinking to the minimum radius, the measured loading peak decrease. As a result, in this work, the pressure field caused by bubble oscillation must take consideration of the vertical moving of bubble for the big change of centrifugal force.

4.1. Analytical model

On account of the fact that the inherent nature of the materials is mainly related to the electromagnetic forces, so the basic material properties in the centrifugal model can be regarded as to be the same with the conventional model [25]. The numerical model was established under the same experimental condition (Fig. 10), which was composed by three parts, namely, water, steel plate and cement mortar. Since the response of cement mortar is not the concern of this study, it was treated as discrete rigid body considering its specific shape and meshed with 22650 R3D4 4-node 3-D bilinear rigid quadrilateral elements [26]. In the simulation, the steel plate adapts the linear elastic model and the material constant used were summarized in Table 2. The plate part was modeled by 21000 C3D8R 8-node linear brick, reduced integration, hourglass control, solid elements, which is not easy to lead to volume locking and save computing cost, and the steel plate was meshed with five elements in the thickness direction to avoid hourglass [27].

Fig. 10Numerical model

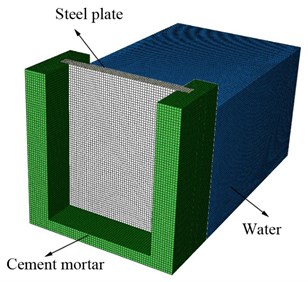
The external fluid water was approximate to a regular cuboid, so it was modeled using acoustic medium element AC3D8R, and the material property constant are also described in Table 2. AC3D8R element is a 8-node linear acoustic brick, reduced integration, hourglass control, solid element, which does not have displacement degrees of freedom [28] (Fig. 10). The explicit time integration method is a conditional stable integration and is closely related to the element characteristic length. Since the wavelength of shockwave increase with the frequency decreasing, the maximum permitted element length of fluid element $L_{\mathrm{m}\mathrm{a}\mathrm{x}}$, can be determined by calculating the upper range of shockwave frequency $f_{\mathrm{m}\mathrm{a}\mathrm{x}}$. The general principal is $L_{\mathrm{m}\mathrm{a}\mathrm{x}}<c_w/(n.f_{\mathrm{m}\mathrm{a}\mathrm{x}})$, where $n$ is the wavelength of the shock wave within the element, and the recommended value is $n\ge$ 6. [29]. And the water domain was established with 444600 elements in the model.

Fig. 11General time-history curves of shock loading

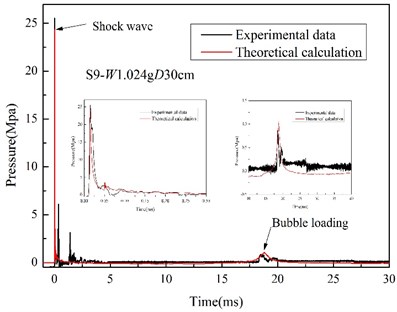
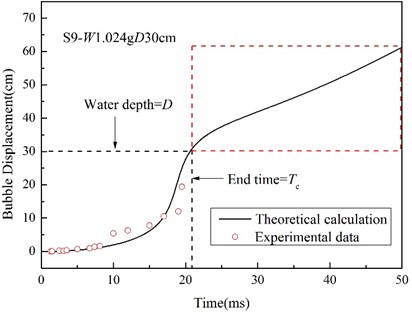
Fig. 12History of floatation displacement of the bubble

4.2. Boundary condition

The interface between steel plate, cement mortar and water respectively adapt acoustic-structure coupling interaction, the interaction between the plate and cement mortar was set as surface to surface contact, and the interfaces between steel plate, cement mortar and the inner walls of model box were separately set as clamped boundary. Although the fluid boundary may lead to the scattering and reflection, which will reinforce or weaken the shock loading, the influence of inner walls and free water surface were ignored in the simulation, considering the small weight of charges and test results. So, the interfaces between fluid and inner walls were set as non-reflective boundary and the reflective effect of free water surface was also not considered.

4.3. Input shock loading

Usually, if the bubble oscillates at a very close distance near the surface of the structure or free surface, either the bubble motion cycle or the maximum bubble radius will be much affected , the bubble will be rejected at the expansion stage, and be drawn at the collapse stage, and a water jet will form ,which can be explained by the Bjerkness effect [31].While, in most cases of this work, the test distance $L$ and water depth $D$ was much bigger than the maximum bubble radius $r_{\mathrm{m}\mathrm{a}\mathrm{x}}$ (Fig. 7), namely, $L/r_{\mathrm{m}\mathrm{a}\mathrm{x}}>$ 2 and $D/r_{\mathrm{m}\mathrm{a}\mathrm{x}}>$ 2, so, the experiment condition can be approximately treated as mid-field or far-field underwater explosion [32]. Mu [33] applied MSC. Dytran to study the characteristics of UNDEX bubble under different boundary conditions, and found that when $D/r_{\mathrm{m}\mathrm{a}\mathrm{x}}>$ 2, the free surface will not influence the bubble oscillation, so the Geer and Hunter model can be applied to calculate the bubble motion parameters, which also has been proved in section 3.4 and reference [18]. From the comparison of the bubble motion tested and calculated, the boundary condition do not affect the bubble oscillation for most experiment cases a lot, so the general input loading-time curves of numerical model were approximately calculated from Eqs. (9) and (10). Fig. 11 compares the experimental and theoretical data of shock loading of S9, and considering the obvious bubble flotation, the theoretical vertical displacement-time curve is applied on the source point as a displacement constraint. When the bubble floats to the free water surface, namely the bubble displacement are equal to water depth, the loading input process in FEM analysis will automatically terminate at end time $T_e$. Fig. 12 shows experimental and theoretical displacement of the bubble of S9, and only the data segment in the black dashed are valid.

4.4. Alpha damping effect on the response

Different from the static analysis, the dynamic analysis must consider the effect of structure deformation and motion, such as damping, which refers to the energy dissipation in the actual motion of the structure. Damping exists in most engineering problems, and even though it is only the approximated simulation of the energy absorption features of the structure, rather than the simulation of the physical mechanism bring about this effect, it is very important for obtaining accurate calculation results [34]. And the introduction of a reasonable damping value to the numerical simulation can effectively restrict numerical oscillation and increase the physical damping of the whole calculation system to make the numerical results better reflect the real physical phenomenon.

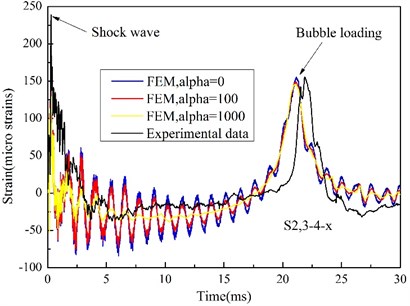
Since the interaction between the plate and UNDEX shock loading is the main concern of this work, the influence of mass ratio damping Alpha is mainly investigated. The Alpha factor define a damping contribution proportionate to element mass matrix, which is related to the absolute nodal velocity of the numerical model, and the effect of the definition of Alpha damping can be compared to the movement of the structure going through a viscous liquid [35], therefore, any nodal movement in the model can lead to the damping force. In the ABAQUS/Explicit analysis, the oscillation of low-frequency response can be effectively adjusted by setting a reasonable Alpha damping [26]. Fig. 13 and Fig. 14 show the effect of Alpha damping on the acceleration and strain response of the steel plate, from which it can be seen that the effect is significant. Both the peak of high-frequency responses caused by shock wave impact and low-frequency responses induced by bubble pulse has a little decline with Alpha damping increasing. However, comparing with high-frequency responses, low-frequency responses are more sensitive to the change of Alpha damping. When Alpha damping is very small, the low- frequency responses of acceleration and strain tend to be obvious oscillations, and the acceleration even cannot be distinguished (Fig. 13), while the high-frequency responses almost keep a stable mode of vibration. And by a great deal of trail calculation, the numerical results agree well with the test results when Alpha damping is close to 1000.

Fig. 13Time history of acceleration at measurement point AC-1

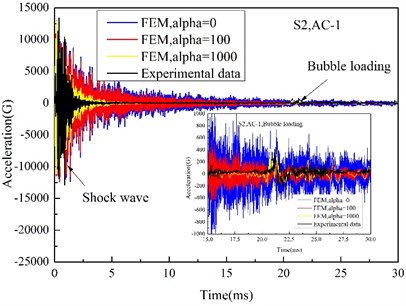
Fig. 14Time history of transverse strain at measurement point 3-4

5.1. Acceleration

Comparison of numerical and tested peak acceleration at various measurement points on the target plate is shown in Table 3. Combined with Fig. 13, it can be seen that the difference between the peak of high-frequency and low-frequency response is very obvious, which is corresponding to the peak loadings and reaches to tens of times. The peak acceleration induced by shock wave is relatively steady, and the peak acceleration caused by bubble pulse decrease gradually for rising centrifugal forces. Owing to the test error, some test and numerical data does not fit very well, and when the standoff distance is very small (15 cm at S10 and 5 cm at S11), the errors between experimental and numerical results all become very big, and it is because that when the charge is very close to the target plate, the formation of bubble jet is greatly affected, which impact the plate like a water hammer [36], and the shock wave and bubble loading will significantly interrelate, so the approximate treatment for free field of a bubble pulse in is not very appropriate again.

5.2. Velocity

Although the particle velocity of the steel plate was not measured in this work, it can be obtained through integration the measured accelerations. And since the acceleration peaks caused by shock wave loading are much bigger than that of the bubble loading, only the velocity responses during shock wave phase are discussed. The period of the integration was from the arrival of the shock front to local cavitation occurred [37]. In the light of the complex constraint boundary of steel plate and initiation condition of charge, some simplification were adopted in the velocity analysis, including that the transmission of shock wave into the plate are ignored, and that the included angle between the straight line through the source point and a given particle and the normal through the source point is equal to the incident and reflection angle of shock wave, and lastly, the upper surface of the plate part exposed to the air is handled as a clamped boundary. Rajendran [38] have derived the particle velocity of plate under normal incident shock wave, and an angle parameter $\omega$ were introduced in this paper to calculate the velocity considering the impact at any angle of incidence.

On the basis of boundary continuity, the velocity of the particle on the incident side is calculated as:

And according to Talyor’s theory [39], the total pressure in normal direction, which acted on the air-backed plate can be expressed as:

where $v_p\left(t\right)$ is the normal velocity of the particle on the plate-water boundary, $P_i\left(t\right)$ and $P_r\left(t\right)$ are the incident and reflected shock wave, respectively, $\omega$ is the incident angle, which is equal to reflection angle, and $P_{total}\left(t\right)$is total wall pressure of the plate.

The particle velocity can be obtained by substituting Eq. (1) into Eq. (13) and Eq. (14):

where $m_p$ is plate mass per unit area, and $\beta$ is the characteristic mass ratio. When $P_{total}\left(t\right)$ drop to zero, the plate and fluid will be separate and cavitation occur [37], the acceleration process of plate owing to shock wave stop and the normal velocity of plate particle reach to the maximum, given by:

Fig. 15Relationships between the peak velocity and shock factor

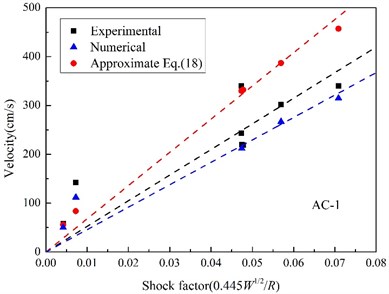
a) AC-1

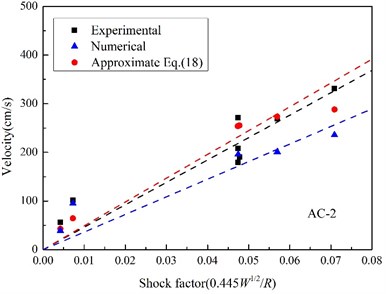
b) AC-2

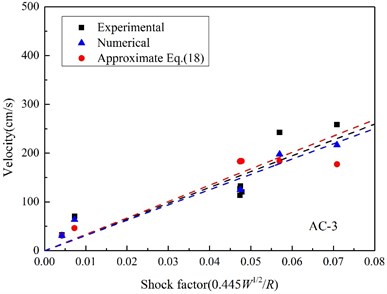
c) AC-3

The time $t_0$, when the total wall pressure drops to zero, can be calculated as:

And $v_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is covert to the theoretical result of Rajendran [38] at $\omega =$ 0.

In UNDEX researches, shock factor is always regarded as an effective characteristic parameter indicating shock energy of UNDEX shock wave, and a shock factor is adopted in this paper to evaluate the velocity response, which is defined as [40]:

Fig. 15 shows the maximum velocity obtained by integrating measured acceleration, approximated by Eq. (18) with peak pressure, and the velocity calculated by the finite element method. All scattered points of peak velocity are linear fitted with the shock factor from the original point, and it can be found that the linear correlation between the peak velocity and the shock factor is much better at the position, where it is much closer to the area the shock wave vertically impact. In particular, when the standoff distance reduces to a certain extent (in Fig. 15(c)), the peak velocity calculated by Eq. (18) begins to decrease with shock factor increasing, which is not consistent with the experimental and numerical results, and it is because of the approximation of the incident angle. When the target position is far from the point shock wave vertically incidents upon, the approximated oblique incidence angle is too big and not reasonable again.

5.3. Strain

In this work, all the strain gauges were firmly adhered to the steel plate, and the experimental and numerical peak strain (S1, S2, S4 and S5) at various measurement points were indicated in Fig. 16 and Fig. 17. The peak strain caused by shock wave in experiment are relatively decentralized for test errors, and most of the experimental peak strains induced by bubble pulse well match the numerical peaks. From the numerical results, it is can be seen that the peak strains induced by shock wave remain stable when centrifugal force changing, the peak strains due to bubble pulse also fall with the centrifugal force increasing, just like the peak accelerations, however, the peak strains induced by the two factors are very close, which is totally different from the acceleration responses.

Fig. 16Peak strain caused by UNDEX shock wave

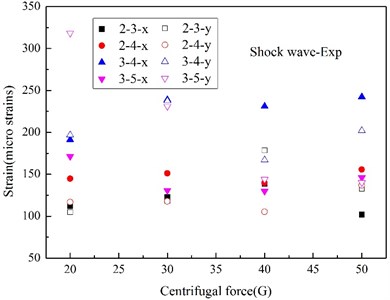
a) Experimental [19]

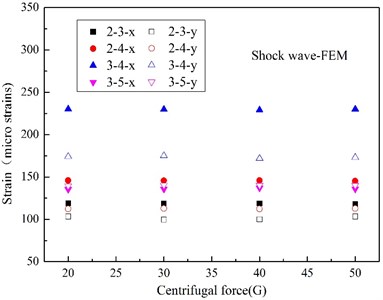
b) Numerical

According to the modal analysis theory on distributed strain measurement [41], the strain response is more similar to the displacement response than the acceleration response, and it is more sensitive to the low-frequency response from the angle of time-frequency domain, which are the responses caused by bubble pulse in this work. Although the pressure of bubble pulse is much lower than that of the shock wave, the duration time of bubble pulse is much higher than that of shock wave, so, even though the high-frequency responses of the strain and acceleration are similar, the change amplitudes of the low-frequency responses of the strain are much higher in contrast to the acceleration responses for the accumulation of time domain. In other words, the strain responses are more sensitive to time accumulation than the acceleration responses. Moreover, from the angle of shock energy, although there is a big difference between the peak pressure of the shock wave and the bubble pulse, the shock energy carried by shock wave and bubble are close [20], so, the difference between the acceleration and strain response can illustrates that the strain response is tightly related to shock energy. And actually, Rajendran has [42] deduced the maximum equivalent strain at one position of the plate in the light of air-backed steel plate impacted only by shock wave, which can be expressed as a function related to peak pressure and decay time, and it can also indirectly elucidate this phenomenon.

Fig. 17Peak strain caused by bubble pulse

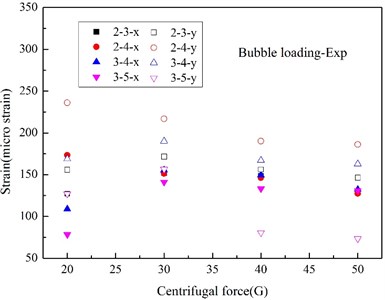
a) Experimental

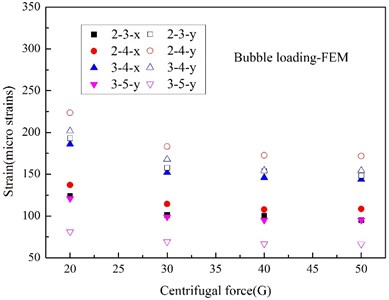
b) Numerical