Free vibration of basalt fiber reinforced polymer (FRP) laminated variable thickness plates with intermediate elastic support using finite strip transition matrix (FSTM) method

scite shows how a scientific paper has been cited by providing the context of the citation, a classification describing whether it supports, mentions, or contrasts the cited claim, and a label indicating in which section the citation was made.

Abstract

This paper presents a semi-analytical method to investigate the effect of intermediate elastic support on the natural frequencies of basalt fiber reinforced polymer (FRP) laminated, variable thickness plates based on the finite strip transition matrix (FSTM) method. The plate has a uniform thickness in $x$ direction and varying thickness $h (y)$ in $y$ direction. A singular value decomposition algorithm is employed at the intermediate support to eliminate the dependence of the solution of the first span on another span. By a new treatment of the intermediate line support, the dimension of the final matrix of the general solution will be the same as that of plates without intermediate support. Numerical results for different combinations of classical boundary conditions at the plate edges with different elastic restraint coefficients ( $K_{T}$ ) for intermediate elastic support are presented to obtain the first six frequency parameters. The illustrated results are in excellent agreement with solutions available in the literature, thus validating the accuracy and reliability of the proposed technique.

1. Introduction

Continuous plates and plates with intermediate stiffeners are very common in many engineering fields such as aerospace industries, civil engineering and marine engineering. Exact solutions of such plates are available only for some boundary conditions. For example, if two opposite sided are simply supported and the other sides may be any combinations of elastic, clamped and free, a Levy-type solution can be obtained for rigid stiffners [1].

In general, a numerical approach or an approximate method must be employed to find the natural frequencies and the mode shapes for different combinations of the boundary conditions. The vibration of plates with intermediate support attracts many researchers.

Xiang and Liew [1] presented an exact (Levy-type) solution for multi-span rectangular mindlin plates with two opposite edges simply supported. Abrate and Foster [2] used Rayleigh-Ritz method to investigate the free vibrations of rectangular composite plates with arbitrary number of intermediate line supports. Cheung and Zhou [3] used Rayleigh-Ritz method to study vibrations of symmetric laminated rectangular plates with intermediate supports. Liew and Wang [4] studied vibration of skew plates with internal line support using the pb-2 Rayleigh-Ritz method. Cheung and Zhou [5] used a set of static beam functions to analyze the vibration of orthotropic rectangular plates with intermediate elastic support. Xiang et al. [6] reported free vibration behavior of laminated seven composite plates based on the $n$ th order shear deformation theory and this theory satisfies the zero transverse shear stress boundary conditions. Thai and Kim [7] examined the free vibration responses of laminated composite plates using two variables refined plate theory. Ovesy and Fazilati [8] employed the third order shear deformation theory for buckling and free vibration finite strip analysis of composite plates with cutout based on two different modeling approaches (semi-analytical and spline method). Dozio [9] presented accurate upper-bound solutions for free in-plane vibrations of single-layer and symmetrically laminated rectangular composite plates with an arbitrary combination of clamped and free boundary conditions. He used Rayleigh-Ritz method to calculate in-plane natural frequencies and modes shapes with a simple, stable and computationally efficient set of trigonometric functions. Asadi et al. [10] investigated the vibration analysis of axially moving functionally graded plates with internal line supports and temperature-dependent properties using harmonic differential quadrature method. They studied plate vibration which was subjected to static in-plane forces while out-of-plane loading was dynamic. Al-Tabey [11] presented the finite strip transition matrix technique (FSTM) and semi-analytical method to obtain the natural frequencies and mode shapes of symmetric angle-ply Graphite/Epoxy laminated composite variable thickness rectangular plate with classical boundary conditions (SSFF). Thinh et al. [12] examined the bending and vibration analysis of multi-folding laminate composite plate using finite element method based on the first order shear deformation theory (FSDT). They investigated the effect of folding angle on deflections, natural frequencies and transient displacement response for different boundary conditions of the plate. Ducceschi [13] studied the nonlinear vibrations of thin rectangular plates by developing of a numerical code able to simulate without restrictions. He described the large spectrum of dynamical features by the von Kármán equations. Yadav et al. [14] presented the free vibration analysis of stiffened isotropic plate by means of finite element method. They studied the effect of different boundary conditions, stiffeners location, thickness ratio, stiffener thickness to plate thickness and aspect ratio on the vibration analysis of stiffened isotropic plate, and calculated natural frequencies using Block-Lanczos algorithm. Küçükrendeci and Morgül [15] investigated the effects of elastic boundary conditions on the linear free vibrations. They found that frequency parameters increase when boron/epoxy used.

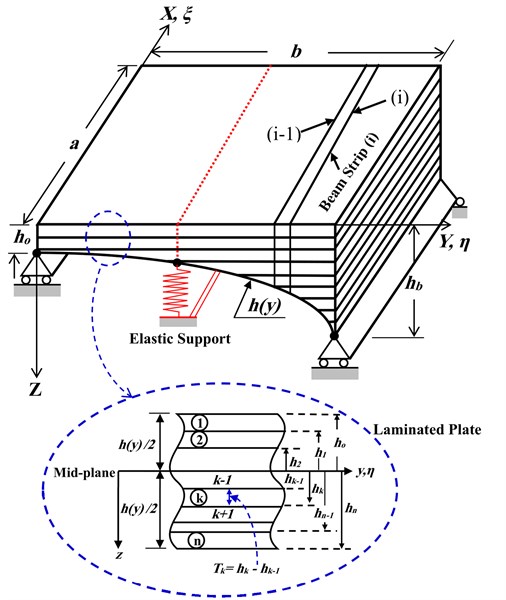
Semi-analytical methods are welcomed in the literature as an alternative to the exact solution. In this paper a semi-analytical method, the finite strips transition matrix (FSTM) method [16] has been employed to investigate the free vibration of basalt fiber reinforced polymer (FRP) laminated variable thickness rectangular plates with intermediate elastic support as shown in Fig. 1. A new treatment of the elastic intermediate boundary conditions using a singular values decomposition algorithm is introduced in this paper. Four different classical boundary conditions are considered in the analysis with different elastic restraint coefficients ( $K_{T}$ ) for intermediate elastic support to obtain the first six frequency parameters, some new data which can serve as the benchmark for further research are presented in this work.

2. Theory and formulation

2.1. Governing equations

The partial differential equation governing the vibration of symmetrically, angle-ply laminated, variable thickness, rectangular plates under the assumption of the classical deformation theory in terms of the plate deflection $w_{o} (x, y, t)$ is given by [17]:

1

$D_{11} \frac{\partial^{4} w_{o}}{\partial x^{4}} + 4 D_{16} \frac{\partial^{4} w_{o}}{\partial x^{3} \partial y} + 2 (D_{12} + 2 D_{66}) \frac{\partial^{4} w_{o}}{\partial x^{2} \partial y^{2}} + 4 D_{26} \frac{\partial^{4} w_{o}}{\partial x \partial y^{3}} + D_{22} \frac{\partial^{4} w_{o}}{\partial y^{4}}$

$= - m_{o} \frac{h (y)}{h_{o}} \frac{\partial^{2} w_{o}}{\partial t^{2}} .$

Or in contraction form:

2

$D_{11} W_{x x x x} + 4 D_{16} W_{x x x y} + 2 (D_{12} + 2 D_{66}) W_{x x y y} + 4 D_{26} W_{x y y y} + D_{22} W_{y y y y}$

$= - m_{o} \frac{h (y)}{h_{o}} W_{t t},$

where: $m_{o} = ρ h_{o}$ , the flexural rigidities $D_{i j}$ of the plate are given by:

3

$D_{i j} = \frac{1}{3} \frac{h^{3} (y)}{h_{o}^{3}} \sum_{k = 1}^{n} {[({\bar{Q}}_{i j})]}_{k} (h_{o k}^{3} - h_{o k - 1}^{3}), i, j = 1, 2, 3 .$

where $h_{o k}$ is the distance from the middle-plane of the plate according to $h_{o}$ to the bottom of the $h_{o t h}$ layer as shown in Fig. 1. And $\bar{Q_{i j}^{k}}$ are the plane stress transformed reduced stiffness coefficients of the lamina in the laminate cartesian coordinate system. They are related to reduce stiffness coefficients of the lamina in the material axes of lamina $Q_{i j}^{k}$ by proper coordinate relationships they can be expressed in terms of the engineering notations as:

4

$Q_{i j} = [\begin{array}{l} Q_{11} & Q_{12} & Q_{13} \\ Q_{12} & Q_{22} & Q_{23} \\ Q_{13} & Q_{23} & Q_{66} \end{array}] = [\begin{matrix} \frac{E_{11}}{(1 - υ_{12} υ_{21})} & \frac{υ_{21} E_{11}}{(1 - υ_{12} υ_{21})} & 0 \\ \frac{υ_{21} E_{11}}{(1 - υ_{12} υ_{21})} & \frac{E_{22}}{(1 - υ_{21} υ_{12})} & 0 \\ 0 & 0 & G_{12} \end{matrix}],$

where: $E_{11}$ , $E_{22}$ are the longitudinal and transverse Young’s moduli parallel and perpendicular to the fiber orientation, respectively and $G_{12}$ is the plane shear modulus of elasticity, $υ_{12}$ and $υ_{21}$ are the Poisson coefficients.

Fig. 1The geometrical model of Basalt FRP laminated variable thickness rectangular plate with intermediate elastic support

The substitution of Eq. (3) into Eq. (2) and after some derivation steps [18], the governing Partial differential equation can be written in form:

5

$D_{11} \frac{h^{3} (y)}{h_{o}^{3}} W_{x x x x} + (\frac{2 (D_{12} + 2 D_{66})}{h_{o}^{3}}) \frac{\partial h^{3} (y)}{\partial y} W_{x x y} + (\frac{2 (D_{12} + 2 D_{66})}{h_{o}^{3}}) h^{3} (y) W_{x x y y}$

$+ D_{16} \frac{h^{3} (y)}{h_{o}^{3}} W_{x x x y} + (\frac{4 D_{26}}{h_{o}^{3}} \frac{\partial^{2} h^{3} (y)}{\partial y^{2}}) W_{x y} + \frac{4 D_{26}}{h_{o}^{3}} h^{3} (y) W_{x y y y} + \frac{8 D_{26}}{h_{o}^{3}} \frac{\partial h^{3} (y)}{\partial y} W_{x y y}$

$+ (\frac{D_{22}}{h_{o}^{3}} \frac{\partial^{2} h^{3} (y)}{\partial y^{2}}) W_{y y} + \frac{D_{22}}{h_{o}^{3}} h^{3} (y) W_{y y y y} + \frac{2 D_{22}}{h_{o}^{3}} \frac{\partial h^{3} (y)}{\partial y} W_{y y y} = - m_{o} \frac{h (y)}{h_{o}} W_{t t} .$

The equation of motion Eq. (5) can be normalized using the non-Dimensional variables $ξ$ and $η$ as follows:

6

$ψ_{1} \frac{1}{a^{4}} W_{ξ ξ ξ ξ} + \frac{2 ψ_{2}}{h^{3} (η)} \frac{1}{a^{2} b} \frac{\partial h^{3} (η)}{\partial η} W_{ξ ξ η} + 2 ψ_{2} \frac{1}{a^{2} b^{2}} W_{ξ ξ η η} + ψ_{3} \frac{1}{a^{3} b} W_{ξ ξ ξ η}$

$+ 4 ψ_{4} \frac{1}{a b^{3}} W_{ξ η η η} + \frac{1}{a b} \frac{4 ψ_{4}}{h^{3} (η)} \frac{\partial^{2} h^{3} (η)}{\partial η^{2}} W_{ξ η} + \frac{8 ψ_{4}}{h^{3} (η)} \frac{1}{a b^{2}} \frac{\partial h^{3} (η)}{\partial η} W_{ξ η η}$

$+ \frac{1}{b^{2}} \frac{1}{h^{3} (η)} \frac{\partial^{2} h^{3} (η)}{\partial η^{2}} W_{η η} + \frac{1}{b^{4}} W_{η η η η} + \frac{2}{h^{3} (η)} \frac{1}{b^{3}} \frac{\partial h^{3} (η)}{\partial η} W_{η η η} = - \frac{m_{o}}{D_{22}} \frac{h_{o}^{2}}{h^{2} (η)} W_{t t},$

where $β = a / b$ is the aspect ratio, and:

$ξ = \frac{x}{a}, η = \frac{y}{b}, ψ_{1} = \frac{D_{11}}{D_{22}}, ψ_{2} = \frac{(D_{12} + 2 D_{66})}{D_{22}}, ψ_{3} = \frac{D_{16}}{D_{22}}, ψ_{4} = \frac{D_{26}}{D_{22}} .$

2.2. Boundary conditions

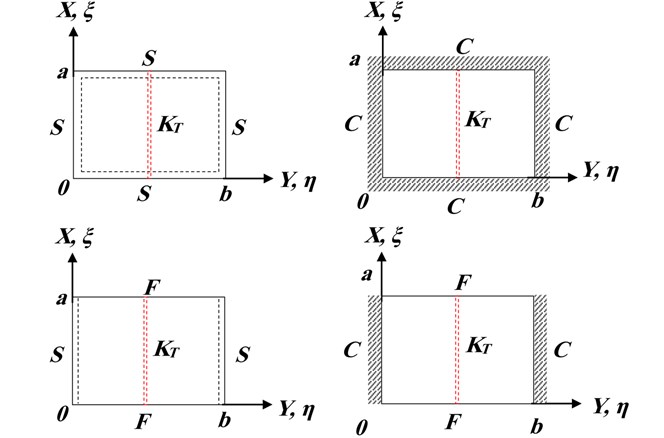
In this paper, the boundary conditions along the $x$ -direction and $y$ -direction are considered by any combinations of the classical boundary conditions such as simply supported, clamped, or free. For the purpose of clarity, the symbol SFSC for example, means a plate having simply supported, free, simply supported and clamped edges at the boundaries, $x =$ 0, $y = b$ , $x = a$ , and $y =$ 0, respectively (start anticlockwise from the left edge of the plate). In the numerical computations, four different classical boundary conditions are considered in the analysis SSSS, CCCC, SSFF and CCFF as shown in Fig. 2.

Fig. 2Representation of different support condition for the analysis

Simply supported edges:

7

${w_{o}|}_{ξ = 0,1} = 0, \frac{1}{a^{2}} {\frac{\partial^{2} w_{o}}{\partial ξ^{2}}|}_{ξ = 0,1} = 0, {w_{o}|}_{η = 0,1} = 0, \frac{1}{b^{2}} {\frac{\partial^{2} w_{o}}{\partial η^{2}}|}_{η = 0,1} = 0 .$

Clamped supported edges:

8

${w_{o}|}_{ξ = 0,1} = 0, {\frac{1}{a} \frac{\partial w_{o}}{\partial ξ}|}_{ξ = 0,1} = 0, {w_{o}|}_{η = 0,1} = 0, \frac{1}{b} {\frac{\partial w_{o}}{\partial η}|}_{y = 0,1} = 0 .$

Free edges:

9

$\frac{1}{a^{3}} {\frac{\partial^{3} w_{o}}{\partial ξ^{3}}|}_{ξ = 0,1} = 0, \frac{1}{a^{2}} {\frac{\partial^{2} w_{o}}{\partial ξ^{2}}|}_{ξ = 0,1} = 0, {\frac{1}{b^{3}} \frac{\partial^{3} w_{o}}{\partial η^{3}}|}_{η = 0,1} = 0, {\frac{1}{b^{2}} \frac{\partial^{2} w_{o}}{\partial η^{2}}|}_{η = 0,1} = 0 .$

2.2.1. Intermediate elastic line support

Since the treatment of the intermediate elastic line support conditions are the main objective of this paper we presented it in more details. At the intermediate elastic line support, $y = b / 2$ , the displacement must vanish and the moment must be continuous, i.e.:

10

$K_{T} w_{o} = - 2 ψ_{3} \frac{1}{a^{3}} \frac{\partial^{3} w_{o}}{\partial ξ^{3}} - \frac{1}{b^{3}} \frac{\partial^{3} w_{o}}{\partial η^{3}} - ψ_{5} \frac{1}{a^{2} b} \frac{\partial^{2} w_{o}}{\partial ξ^{2} \partial η} - 4 ψ_{4} \frac{1}{a b^{2}} \frac{\partial^{3} w_{o}}{\partial ξ \partial η^{2}},$

11

$\frac{1}{b} {\frac{\partial w_{o}}{\partial η^{}}|}_{η = 1^{-} / 2} = \frac{1}{b} {\frac{\partial w_{o}}{\partial η^{}}|}_{η = 1^{+} / 2},$

12

${- 2 ψ_{3} \frac{1}{a^{3}} \frac{\partial^{3} w_{o}}{\partial ξ^{3}} - \frac{1}{b^{3}} \frac{\partial^{3} w_{o}}{\partial η^{3}} - ψ_{5} \frac{1}{a^{2} b} \frac{\partial^{2} w_{o}}{\partial ξ^{2} \partial η} - 4 ψ_{4} \frac{1}{a b^{2}} \frac{\partial^{3} w_{o}}{\partial ξ \partial η^{2}}|}_{β = 1^{-} / 2}$

${= - 2 ψ_{3} \frac{1}{a^{3}} \frac{\partial^{3} w_{o}}{\partial ξ^{3}} - \frac{1}{b^{3}} \frac{\partial^{3} w_{o}}{\partial η^{3}} - ψ_{5} \frac{1}{a^{2} b} \frac{\partial^{2} w_{o}}{\partial ξ^{2} \partial η} - 4 ψ_{4} \frac{1}{a b^{2}} \frac{\partial^{3} w_{o}}{\partial ξ \partial η^{2}}|}_{β = 1^{+} / 2},$

where: $K_{T}$ is the elastic restraint coefficient given by: $K_{T} = T_{b / 2} b^{3} / D_{22}$ , $T$ is translational stiffness per unit length, $ψ_{5} = (D_{12} + 4 D_{66}) / D_{22}$ .

2.3. Finite strip transition matrix (FSTM) method

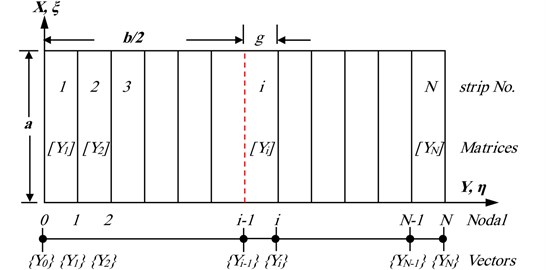
The method is made when such a shape function is not conveniently obtained in case of discussing the plate problems by series. The plate may be divided into $N$ discrete longitudinal strips spanning between supports as shown in Fig. 3. Simple basic displacement interpolation functions may then be used to represent displacement field within and between individual strips.

For a plate striped in the $ξ$ -direction as shown in Fig. 3, the shape function $W (ξ, η, t)$ may be assumed in the form:

13

$W (ξ, η, t) = \sum_{i = 0}^{N} X_{i} (ξ) Y_{i} (η) e^{i ω_{t}},$

where: $Y_{i} (η)$ is unknown function to be determined and $X_{i} (ξ)$ is chosen a priori, the basic function in $ξ$ -direction. The most commonly used is the Eigen function obtained from the solution of the differential equation of a beam vibration under the prescribed conditions of the stripe at $ξ =$ 0 and $ξ =$ 1. By substituting of Eq. (13) into Eq. (6), multiplying both sides by $X_{j} (x)$ and after some derivatives, we can find:

14

$\sum_{i = 0}^{N} \sum_{j = 0}^{M} \frac{β^{4}}{f_{3} (η)} Y_{i, η η η η} + 2 β^{3} a \frac{f_{1} (η)}{f_{3} (η)} Y_{i, η η η}$

$+ (\frac{2 ψ_{2} β^{2}}{f_{3} (η)} \frac{c_{i j}}{a_{i j}} + 8 ψ_{4} β^{2} a \frac{f_{1} (η)}{f_{3} (η)} \frac{b_{i j}}{a_{i j}} + β^{2} a^{2} \frac{f_{2} (η)}{f_{3} (η)}) Y_{i, η η}$

$+ (2 ψ_{2} β a \frac{f_{1} (η)}{f_{3} (η)} \frac{c_{i j}}{a_{i j}} + \frac{ψ_{3} β}{f_{3} (η)} \frac{d_{i j}}{a_{i j}} + 4 ψ_{4} β a^{2} \frac{f_{2} (η)}{f_{3} (η)} \frac{b_{i j}}{a_{i j}} + \frac{4 ψ_{4} β^{3}}{f_{3} (η)} \frac{b_{i j}}{a_{i j}}) Y_{i, η}$

$+ (\frac{ψ_{1}}{f_{3} (η)} \frac{e_{i j}}{a_{i j}} - Ω^{2}) Y_{i} = 0,$

where:

$Ω^{2} = \frac{m_{o} h (η) ω^{2} a^{4}}{h_{o} D_{22}}, f_{1} (η) = \frac{1}{h^{3} (η)} \frac{\partial h^{3} (η)}{\partial η}, f_{2} (η) = \frac{1}{h^{3} (η)} \frac{\partial^{2} h^{3} (η)}{\partial η^{2}},$

$f_{3} (η) = \frac{h_{o}^{2}}{h^{2} (η)}, a_{i j} = \int_{0}^{1} X_{i} X_{j} d ξ, b_{i j} = \int_{0}^{1} X_{j} X_{i, ξ} d ξ,$

$c_{i j} = \int_{0}^{1} X_{j} X_{i, ξ ξ} d ξ, d_{i j} = \int_{0}^{1} X_{j} X_{i, ξ ξ ξ} d ξ, e_{i j} = \int_{0}^{1} X_{j} X_{i, ξ ξ ξ ξ} d ξ .$

Fig. 3Finite strip simulation on plate

From the beam Eigen function orthogonality, $a_{i j} = e_{i j} = 0$ for $i \neq j$ , this agree for all types of boundary conditions except for plates having free edges in the $ξ$ -direction. The governing differential Eq. (14) can be written in form:

15

$\sum_{i = 0}^{N} \sum_{j = 0}^{M} E_{i j} Y_{i}^{''''} + \frac{{(U_{1})}_{i j}}{{(U_{0})}_{i j}} Y_{i}^{'''} + \frac{{(U_{2})}_{i j}}{{(U_{0})}_{i j}} Y_{i}^{''} + \frac{{(U_{3})}_{i j}}{{(U_{0})}_{i j}} Y_{i}^{'} + \frac{{(U_{4})}_{i j} - λ^{2}}{{(U_{0})}_{i j}} Y_{i} = 0,$

where:

${(U_{0})}_{i j} = β^{4} t_{1} (η) E_{i j}, {(U_{1})}_{i j} = 2 β^{3} a t_{2} (η) E_{i j},$

${(U_{2})}_{i j} = (2 ψ_{2} β^{2} t_{1} (η) \frac{c_{i j}}{a_{i j}} + 8 ψ_{4} β^{2} a t_{2} (η) \frac{b_{i j}}{a_{i j}} + β^{2} a^{2} t_{3} (η)),$

${(U_{3})}_{i j} = (2 ψ_{2} β a t_{2} (η) \frac{c_{i j}}{a_{i j}} + ψ_{3} β t_{1} (η) \frac{d_{i j}}{a_{i j}} + 4 ψ_{4} β a^{2} t_{3} (η) \frac{b_{i j}}{a_{i j}} + 4 ψ_{4} β^{3} t_{1} (η) \frac{b_{i j}}{a_{i j}}),$

${(U_{4})}_{i j} = ψ_{1} t_{1} (η) \frac{e_{i j}}{a_{i j}},$

and $[E_{i j}] = i \times j$ unit matrix.

A system of coupled fourth order equations are obtained which can be reduced to a system of first order differential equation:

16

$\frac{d}{d η} {\{Y_{k}\}}_{i j} = {[A_{i}]}_{k} {\{Y_{k}\}}_{i j},$

where: $k =$ 1, 2, 3,…, $N$ , $i =$ 1, 2, 3,…, $N$ , $j =$ 1, 2, 3,…, $M$ , coefficients of the matrix ${[A_{i}]}_{k}$ in equation, in general, are functions of $η$ and the eigenvalue parameter $Ω$ . The vector $Y_{k}$ is given by:

17

$Y_{k} = (\begin{array}{l} {\bar{Y}}_{1} & {\bar{Y}}_{2} & \dots & {\bar{Y}}_{i} & \dots & {\bar{Y}}_{N} \end{array}),$

where:

18

${\bar{Y}}_{i} = (\begin{array}{l} Y_{i} & Y_{i}^{'} & Y_{i}^{''} & Y_{i}^{'''} \end{array}) .$

The relation under which the continuity conditions between the striped plates are satisfied may be expressed as:

19

${\{Y_{i}\}}_{j} = {[T_{i}]}_{j} {\{Y_{i - 1}\}}_{j},$

where: ${[T_{i}]}_{j}$ is called the transition matrix of the strip $i$ while ${\{Y_{i}\}}_{j}$ and ${\{Y_{i - 1}\}}_{j}$ are the nodal vectors of the boundaries $i$ and $i - 1$ . The solution is found using 2 $N$ -number of initial vectors $\{Y_{0}\}$ at $η =$ 0. The transition matrix, Eq. (19) is applied across the stripped plate until just before the intermediate support at $y = b / 2$ , $η = 1 / 2$ is reached. Thus, 2 $N$ -number of solutions $S_{i}$ can be obtained. The true solutions $[S]$ can be written as a linear combination of these solutions as:

20

$[S] = \sum_{i = 1}^{2 N} C_{i} S_{i},$

where $C_{i}$ are arbitrary constants, these constants can be determined by satisfying 2 $N$ -number of boundary conditions at $η =$ 1/2 in Eqs. (10) and (12) of the intermediate elastic line support. And the matrix $[S]$ forms a standard eigenvalue problem. The natural frequencies of the system can be obtained from the conditions that the detainment of the $S$ must vanish. An iteration algorithm is implemented to compute the natural frequency of the system and hence the constants $C_{i}$ , $i =$ 1, 2, 3,…, 2 $N$ .

3. Results and discussion

In this section, the finite strip transition matrix (FSTM) approach is employed to investigate the free vibration of symmetrically laminated, angle-ply, variable thickness rectangular plates with intermediate elastic support in one direction with different elastic restraint coefficient ( $K_{T}$ ). The basalt FRP laminate composite plate was manufactured using five symmetrically, angle-ply, laminates with the fiber orientations [45°/–45°/45°/–45°/45°] of basalt fiber and a polymer resin matrix. The corresponding elastic modulus values were $E_{1} =$ 96.74 GPa, $E_{2} = E_{3} =$ 22.55 GPa, and the Shear modulus values were $G_{1} = G_{3} =$ 10.64 GPa, $G_{2} =$ 8.73 GPa. Poisson coefficients were $υ_{1} = υ_{3} =$ 0.3, $υ_{2} =$ 0.6 and the density was 2700 kg/m³.

The frequency parameter $Ω$ is evaluated in non-dimensional form, expressed as:

21

$Ω = \sqrt{\frac{m_{o} h (η) ω^{2} a^{4}}{h_{o} D_{22}}} .$

The plate with linear variable thickness, $h (y)$ is used (see Appendix) in non-dimensional form:

22

$h (η) = 1 + Δ η,$

where: $Δ$ is the tapered ratio of plate given by $Δ = (h_{b} - h_{o}) / h_{o}$ , $(h_{o})$ is the thickness of the plate at $η =$ 0 and ( $h_{b}$ ) is the thickness of the plate at $η =$ 1.

3.1. Convergence study and accuracy

In this subsection, a convergence investigation is carried out for the proposed method, first six frequencies are calculated and compared with available results in literatures. Table 1 presents a convergence and comparison study for isotropic, square ( $β =$ 1.0), uniform thickness ( $Δ =$ 0) plates with a mid-line support in each direction, the plate material has mechanical properties of $υ_{1} = υ_{2} =$ 0.3, $D_{11} = D_{22} = D = E h^{3} / [12 (1 - υ^{2})]$ , $D_{66} = (1 - υ) D / 2$ . In this study the non-dimensional frequency parameter $Ω$ become $Ω = {(ρ h ω^{2} a^{4} / D)}^{1 / 2}$ . Two different classical boundary conditions are considered in the computational SSSS and CCCC. The computational results which are compared with values available from literatures [5, 19-21]. A very close agreement is observed.

Table 2 presented a convergence and comparison study for fully simply supported (SSSS) and fully clamped (CCCC) square ( $β =$ 1.0), uniform thickness ( $Δ =$ 0) plates with elastic foundation support. The elastic coefficient is taken equal to 500, 1390.2 for SSSS and CCCC respectively. The plates are manufactured from E-glass/ epoxy material with the following properties are $υ_{1} = υ_{3} =$ 0.23, $D = E h^{3} / [12 (1 - υ^{2})]$ , $D_{66} = (1 - υ) D / 2$ . In this study the non-dimensional frequency parameter $Ω$ become $Ω = {(ρ h ω^{2} a^{4} / π D)}^{1 / 2}$ and foundation elastic restraint coefficient is given by $K_{T} = k_{f} a^{4} / D$ . From Table 2 it can be observed that the computational results are in an excellent agreement with exact frequency parameters presented in References [22, 23] and stable and fast convergence can be achieved with only a few terms of series solution ( $N =$ 3 to 7). This validates the precision of the semi-analytical finite strip transition matrix (FSTM) technique.

Table 1Convergence study of the first six frequency parameters of the isotropic square plates with a mid-line support in each direction

	$N$	$Ω_{1}$	$Ω_{2}$	$Ω_{3}$	$Ω_{4}$	$Ω_{5}$	$Ω_{6}$
SSSS	1	78.866	94.506	94.506	108.125	197.311	197.311
	2	78.887	94.529	94.529	108.159	197.324	197.324
	4	78.910	94.546	94.546	108.184	197.350	197.350
	6	78.928	94.568	94.568	108.211	197.369	197.369
Ref [5]		78.957	94.590	94.590	108.240	197.392	197.392
Ref [19]		78.96	94.68	94.72	108.44	197.40	198.96
Ref [20]		78.958	94.826	94.826	108.41	197.50	197.50
Ref [21]		78.957	94.585	94.585	108.22	197.39	197.33
CCCC	2	108.222	127.346	127.346	144.026	242.386	242.386
	4	108.243	127.365	127.365	144.048	242.758	242.758
	5	108.259	127.382	127.382	144.071	242.773	242.773
	7	108.282	127.398	127.398	144.099	242.801	242.801
Ref [5]		108.299	127.417	127.417	144.109	242.818	243.778

Table 2Convergence study of the first four frequency parameters of the isotropic square plates with elastic foundation

	$N$	$K_{T}$	$Ω_{1}$	$Ω_{2}$	$Ω_{3}$	$Ω_{4}$
SSSS	2	500	3.0210	5.4828	5.4828	8.3017
	3	500	3.0211	5.4836	5.4836	8.3019
	4	500	3.0212	5.4842	5.4842	8.3023
	7	500	3.0213	5.4847	5.4847	8.3029
Ref [22]		500	3.0214	5.4850	5.4850	8.3035
Ref [23]		500	3.0216	5.4846	5.4846	8.3051
CCCC	2	1390.2	5.2515	8.3785	8.3785	11.506
	3	1390.2	5.2538	8.3811	8.3811	11.528
	6	1390.2	5.2554	8.3843	8.3843	11.553
	7	1390.2	5.2573	8.3879	8.3879	11.568
Ref [22]		1390.2	5.2588	8.4322	8.4322	11.674
Ref [23]		1390.2	5.2438	8.3129	8.3129	11.546

3.2. Laminated variable thickness plate with intermediate elastic line support

The results from the numerical computations using FSTM approach will be discussed here. Table 3 presents the first six frequencies of a symmetrically, angle-ply, laminated, variable thickness rectangular plate with intermediate elastic line support in one direction as shown in Fig. 1. The aspect ratio of the plate is $β =$ 0.5 and tapered ratio of the plate thickness is $Δ =$ 0.5. Four type of classical boundary conditions (SSSS, CCCC, SSFF and CCFF) as shown in Fig. 2 and different elastic restraint coefficients $K_{T}$ of intermediate elastic line support are considered in the computations to study the effect of intermediate elastic support on the natural frequencies of basalt (FRP) laminated variable thickness rectangular plate. The locations of the intermediate elastic line support is at mid-line of the plate.

Fig. 4Variation of non-dimensional frequencies parameter (Ω) with elastic restraint coefficient (KT)

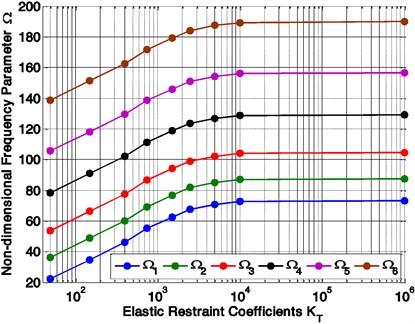
The effect of intermediate elastic support on the non-dimensional frequencies of laminated variable thickness rectangular plate is computed and plotted in Figs. 4 and 5. From this figures, it is observed that the first six frequencies increase with the increasing of the value of elastic restraint coefficient ( $K_{T}$ ) as shown in Fig. 4. Fig. 5 shows the vibration behaviour of the variable thickness rectangular plate under varying elastic restraint coefficient ( $K_{T}$ ). As shown in the Fig. 5, the increasing values of frequencies with small elastic restraint coefficient ( $K_{T}$ ) are higher than the increasing values of frequencies with highest one, and the frequencies at high values of elastic restraint coefficient are almost constant.

After the value of $K_{T}$ increases from 50 onwards, the non-dimensional frequencies parameter are fast raised till value of $K_{T}$ reached 10⁴ and after this value there is almost negligible change in value of Non-dimensional frequencies parameter.

Fig. 5Variation of non-dimensional frequencies parameter (Ω) with different mode number and elastic restraint coefficient (KT)

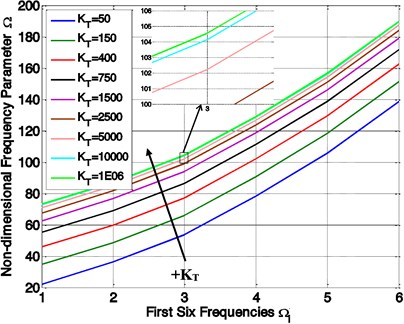
Fig. 6Variation of non-dimensional frequencies parameter (Ω) with elastic restraint coefficient (KT) and boundary conditions

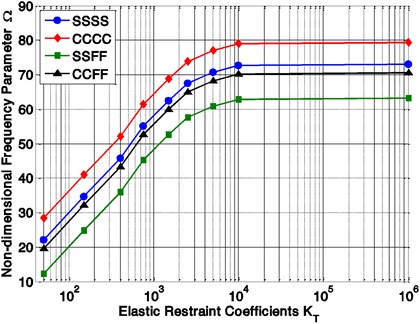
Fig. 7Variation of non-dimensional frequencies parameter (Ω) with different mode number and boundary conditions

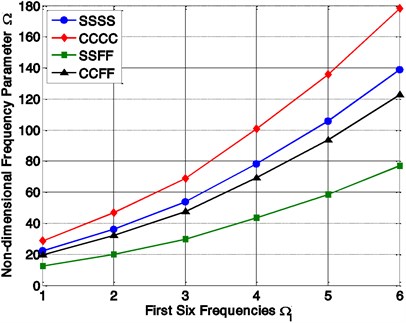
Influence of four different support conditions (SSSS, CCCC, SSFF and CCFF) on the vibration behavior of a symmetrically, angle-ply, laminated, variable thickness rectangular plate is computed and plotted in Figs. 6 and 7, From this figures, it can be seen that the frequencies are showing higher and lower value at fully clamped (CCCC) and semi-simply supported (SSFF) condition, respectively. The other two boundary conditions (SSSS and CCFF) are showing an intermediate value. As shown in the Fig. 6, the non-dimensional frequencies increase with the increase of the elastic restraint coefficient ( $K_{T}$ ) for all kind of support conditions (SSSS, CCCC, SSFF and CCFF).

Table 3The first six frequencies of symmetrically, angle-ply, laminated, variable thickness rectangular plate with intermediate elastic line support for different elastic restraint coefficients, (Δ= 0.5), (β= 0.5)

	$K_{T}$	$Ω_{1}$	$Ω_{2}$	$Ω_{3}$	$Ω_{4}$	$Ω_{5}$	$Ω_{6}$
SSSS	50	22.1450	36.2210	53.5870	78.2360	105.5870	138.6970
	150	34.6580	48.7340	66.1000	90.7490	118.1000	151.2100
	400	45.8453	59.9213	77.2873	101.9363	129.2873	162.3973
	750	55.0692	69.1452	86.5112	111.1602	138.5112	171.6212
	1500	62.4709	76.5469	93.9129	118.5619	145.9129	179.0229
	2500	67.5270	81.6030	98.9690	123.6180	150.9690	184.0790
	5000	70.7832	84.8592	102.2252	126.8742	154.2252	187.3352
	10000	72.7065	86.7825	104.1485	128.7975	156.1485	189.2585
	1E+06	73.1195	87.1955	104.5615	129.2105	156.5615	189.6715
CCCC	50	28.4310	46.5025	68.7979	100.4437	135.5584	178.0668
	150	40.9440	59.0155	81.3109	112.9567	148.0714	190.5798
	400	52.1313	70.2028	92.4983	124.1440	159.2587	201.7672
	750	61.3551	79.4267	101.7221	133.3678	168.4826	210.9910
	1500	68.7569	86.8284	109.1239	140.7696	175.8843	218.3928
	2500	73.8130	91.8845	114.1800	145.8257	180.9404	223.4489
	5000	77.0692	95.1407	117.4361	149.0819	184.1966	226.7050
	10000	78.9925	97.0640	119.3594	151.0052	186.1199	228.6283
	1E+06	79.4055	97.4770	119.7724	151.4182	186.5329	229.0413
SSFF	50	12.2750	20.0773	29.7033	43.3663	58.5270	76.8799
	150	24.7880	32.5903	42.2163	55.8793	71.0400	89.3929
	400	35.9753	43.7777	53.4036	67.0666	82.2273	100.5802
	750	45.1992	53.0015	62.6275	76.2905	91.4511	109.8041
	1500	52.6009	60.4033	70.0293	83.6922	98.8529	117.2058
	2500	57.6570	65.4594	75.0853	88.7483	103.9090	122.2619
	5000	60.9132	68.7155	78.3415	92.0045	107.1652	125.5181
	10000	62.8365	70.6388	80.2648	93.9278	109.0885	127.4414
	1E+06	63.2495	71.0518	80.6778	94.3408	109.5015	127.8544
CCFF	50	19.5928	32.0466	47.4112	69.2194	93.4182	122.7123
	150	32.1058	44.5596	59.9242	81.7324	105.9312	135.2253
	400	43.2931	55.7469	71.1115	92.9197	117.1185	146.4127
	750	52.5170	64.9707	80.3353	102.1436	126.3424	155.6365
	1500	59.9187	72.3725	87.7371	109.5453	133.7442	163.0383
	2500	64.9748	77.4286	92.7932	114.6014	138.8002	168.0944
	5000	68.2310	80.6848	96.0494	117.8576	142.0564	171.3505
	10000	70.1543	82.6081	97.9727	119.7809	143.9797	173.2738
	1E+06	70.5673	83.0211	98.3857	120.1939	144.3927	173.6868

4. Conclusions

The work reported in this paper employs an efficient semi-analytical method for analysing the free vibration of thin basalt fiber reinforced polymer (FRP) laminated variable thickness rectangular plates with intermediate elastic support. A singular value decomposition algorithm has been employed to treat the intermediate support and reduce the dependence of the solutions at the intermediate elastic support. It is observed that the first six frequencies increase with increasing values of elastic restraint coefficient ( $K_{T}$ ) of intermediate elastic support, and the rate of increasing is different. It was found that the increasing rates of frequencies with a small elastic restraint coefficient ( $K_{T}$ ) are higher than the increasing rates of frequencies with highest one, and the frequencies at high values of elastic restraint coefficient are almost constant. On other hand, it observed that the frequencies values were influenced with change of the plate edges support between four different support conditions, for all first six frequencies are showing higher and lower value at fully clamped (CCCC) and semi-simply supported (SSFF) condition, respectively, the other two boundary conditions (SSSS and CCFF) are showing an intermediate value. Accuracy and convergence of solution was examined by comparing the numerical results obtained by the present method with those previously published. The results are in excellent agreement with results from the literature.

References

Xiang Y., Wei G. W. Exact solutions for multi-span rectangular Mindlin plates. Journal of Vibration and Acoustics, Vol. 124, 2002, p. 545-551.

Publisher
Abrate S., Foster E. Vibration of composite plates with intermediate line supports. Journal of Sound and Vibration, Vol. 179, 1995, p. 793-815.

Publisher
Cheung Y. K., Zhou D. Vibration of rectangular plates with elastic intermediate line-supports and edges constraints. Journal of Thin-walled Structures, Vol. 37, 2000, p. 305-331.

Publisher
Liew K. M., Wang C. M. Vibration studies on skew plates: treatment of internal line supports. Journal of Computer and Structures, Vol. 49, Issue 6, 1993, p. 941-951.

Publisher
Cheung Y. K., Zhou D. Vibration analysis of Symmetrically Laminated rectangular plates with intermediate line supports. Journal of Computer and Structures, Vol. 79, 2001, p. 33-41.

Publisher
Xiang S., Jiang S., Bi Z., Jin Y., Yang M. A nth-order meshless generalization of Reddy’s third order shear deformation theory for the free vibration on laminated composite plates. Journal of Composite Structures, Vol. 93, 2011, p. 299-307.

Publisher
Thai H., Kim S. Free vibration of laminated composite plates using two variable refined plate theory. International Journal of Mechanical Sciences, Vol. 52, 2010, p. 626-633.

Publisher
Ovesy H. R., Fazilati J. Buckling and free vibration finite strip analysis of composite plates with cutout based on two different modeling approaches. Journal of Composite Structures, Vol. 94, 2012, p. 1250-1258.

Publisher
Dozio L. In-plane free vibrations of single-layer and symmetrically laminated rectangular composite plates. Journal of Composite Structures, Vol. 93, 2011, p. 1787-1800.

Publisher
Asadi H., Aghdam M. M., Shakeri M. Vibration analysis of axially moving line supported functionally graded plates with temperature-dependent properties. Journal of Mechanical Engineering Science, Vol. 228, Issue 6, 2014, p. 953-969.

Publisher
Al-Tabey W. A. Vibration Analysis of Laminated Composite Variable Thickness Plate Using Finite Strip Transition Matrix Technique and MATLAB Verifications, book MATLAB Applications for the Practical Engineer. Technology and Medicine Open Access Book Publisher, 2014, p. 283-620.

Publisher
Thinh T. I., Binh B. V., Tu T. M. Bending and vibration analysis of multi-folding laminate composite plate using finite element method. Vietnam Journal of Mechanics, Vol. 34, Issue 3, 2012, p. 185-202.

Publisher
Ducceschi M. Nonlinear Vibrations of Thin Rectangular Plates: A Numerical Investigation with Application to Wave Turbulence and Sound Synthesis. Ph.D. Thesis, ENSTA-Paris Tech, 2014.

Search CrossRef
Yadav D. P. S., Sharma A. K., Shivhare V. Free vibration analysis of isotropic plate with stiffeners using finite element method. Journal of Engineering Solid Mechanics, Vol. 3, 2015, p. 67-176.

Publisher
Küçükrendeci I., Morgül Ö. K. The effects of elastic boundary conditions on the linear free vibrations. Journal of Scientific Research and Essays, Vol. 6, Issue 19, 2001, p. 3949-3958.

Publisher
Bert W., Malik M. Free vibration analysis of tapered rectangular plates by differential quadrature method: a semi-analysis approach. Journal of Sound and Vibration, Vol. 190, 1996, p. 41-63.

Publisher
Chakraverty S. Vibration of Plates. CRC Press, Taylor and Francis Group, 2009.

Publisher
Reddy J. N. Mechanics of Laminated Composite Plates and Shells Theory and Analysis. 2nd Ed., CRC Press, Boca Raton London New York Washington, D.C., 2006.

Search CrossRef
Wu C. I., Cheung Y. K. Frequency analysis of rectangular plates continuous in one or two directions. Journal of Earthquake Engineering Structure Dynamics, Vol. 3, 1974, p. 3-14.

Publisher
Kim C. S., Dickinson S. M. The flexural vibration of line supported rectangular plate systems. Journal of Sound Vibration, Vol. 114, 1987, p. 29-42.

Publisher
Leissa A. W. The free vibration of rectangular plates. Journal of Sound and Vibration, Vol. 31, 1973, p. 257-93.

Publisher
Zhou D., Cheung Y. K., Lo S. H., Au F. T. K. Three dimensional vibration analysis of rectangular thick plates on Pasternak foundation. International Journal of Numerical Methods in Engineering, Vol. 59, 2004, p. 1313-1334.

Publisher
Ferreira J. M., Roque C. M. C., Neves A. M. A., Jorge R. M. N., Soares, C. M. M. Analysis of plates on Pasternak foundations by radial basis functions. Journal of Computational Mechanics, Vol. 46, 2010, p. 791-803.

Publisher

Cited by

Proceedings of the 4th International Conference on Advances in Civil and Ecological Engineering Research

Weixing Hong | Mohammad Noori | Hanqing Jiang | Yuhan Liu | Wael A. Altabey

(2023)

Free vibration analysis of laminated elliptic cylindrical panel with varying thickness using a meshfree method

Songhun Kwak | Kwanghun Kim | Gwangil Jong | Yonggum Kim | Kyongjin Pang

(2022)

The Damage Identification in Laminated Composite Plate under Fatigue Load through Wavelet Packet Energy Curvature Difference Method

Wael A. Altabey

(2022)

Proceedings of the 4th International Conference on Intelligent Science and Technology

(2022)

Free vibration analysis of laminated rectangular plates with varying thickness using Legendre-radial point interpolation method

Songhun Kwak | Kwanghun Kim | Sunjong Jon | Jongguk Yun | Chanil Pak

(2022)

2022 International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME)

Wael A. Altabey | Sallam A. Kouritem | Mohammed I. Abouheaf | Nabil Nahas

(2022)

2022 International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME)

Wael A. Altabey | Sallam A. Kouritem | Mohammed I. Abouheaf | Nabil Nahas

(2022)

A strong-form Chebyshev-RPIM meshless solution for free vibration of conical shell panels with variable thickness and fiber curvature

Shuangwei Hu | Rui Zhong | Qingshan Wang | Bin Qin | Wen Shao

(2022)

Selecting optimum levels of wavelet multi‐resolution analysis for time‐varying signals in structural health monitoring

Ahmed Silik | Mohammad Noori | Wael A. Altabey | Ramin Ghiasi

(2021)

Reaching law based sliding mode control for a frame structure under seismic load

Ying Zhao | Mohammad Noori | Wael A. Altabey

(2021)

Experimental and Numerical Assessment on Seismic Performance of Earth Adobe Walls

Zele Li | Mohammad Noori | Wael A. Altabey

(2021)

Deep Learning-Based Crack Identification for Steel Pipelines by Extracting Features from 3D Shadow Modeling

(2021)

Identification of cracks in an Euler–Bernoulli beam using Bayesian inference and closed-form solution of vibration modes

Tianyu Wang | Mohammad Noori | Wael A. Altabey

(2021)

Parameter identification and dynamic response analysis of a modified Prandtl–Ishlinskii asymmetric hysteresis model via least-mean square algorithm and particle swarm optimization

Tianyu Wang | Mohammad Noori | Wael A Altabey | Mojtaba Farrokh | Ramin Ghiasi

(2021)

A Comparison of Three Different Methods for the Identification of Hysterically Degrading Structures Using BWBN Model

Ying Zhao | Mohammad Noori | Wael A. Altabey | Taher Awad

(2019)

Fatigue damage identification for composite pipeline systems using electrical capacitance sensors

Ying Zhao | Mohammad Noori | Wael A Altabey | Zhishen Wu

(2018)

Deep Learning-Based Damage, Load and Support Identification for a Composite Pipeline by Extracting Modal Macro Strains from Dynamic Excitations

Ying Zhao | Mohammad Noori | Wael A. Altabey | Ramin Ghiasi | Zhishen Wu

(2018)

Prediction of natural frequency of basalt fiber reinforced polymer (FRP) laminated variable thickness plates with intermediate elastic support using artificial neural networks (ANNs) method

Wael A. Altabey

(2017)

About this article

Received

05 January 2017

Accepted

12 March 2017

Published

30 June 2017

SUBJECTS

Modal analysis and applications

DOI

https://doi.org/10.21595/jve.2017.18154

Keywords

free vibration

finite strip transition matrix

variable thickness plate

basalt FRP

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2021 02 06

Applying deep learning and wavelet transform for predicting the vibration behavior in variable thickness skew composite plates with intermediate elastic support

Wael A. Altabey

Research article

2019 11 28

Dynamic stiffness method for free vibration analysis of thin functionally graded rectangular plates

Manish Chauhan, Vinayak Ranjan, Prabhakar Sathujoda

Research article

2019 11 28

Free vibration analysis of simply supported rectangular plates

Ganesh Naik Guguloth, Baij Nath Singh, Vinayak Ranjan

Research article

2019 03 15

Modelling on vibration of skew plate with thickness and temperature variation

Reeta Bhardwaj, Naveen Mani

W. A. Altabey, “Free vibration of basalt fiber reinforced polymer (FRP) laminated variable thickness plates with intermediate elastic support using finite strip transition matrix (FSTM) method,” Journal of Vibroengineering, Vol. 19, No. 4, pp. 2873–2885, Jun. 2017, https://doi.org/10.21595/jve.2017.18154

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2017.18154
UR  - https://doi.org/10.21595/jve.2017.18154
TI  - Free vibration of basalt fiber reinforced polymer (FRP) laminated variable thickness plates with intermediate elastic support using finite strip transition matrix (FSTM) method
T2  - Journal of Vibroengineering
AU  - Altabey, Wael A.
PY  - 2017
DA  - 2017/06/30
PB  - JVE International Ltd.
SP  - 2873-2885
IS  - 4
VL  - 19
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Altabey_2017,
	doi = {10.21595/jve.2017.18154},
	url = {https://doi.org/10.21595/jve.2017.18154},
	year = 2017,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {19},
	number = {4},
	pages = {2873--2885},
	author = {Wael A. Altabey},
	title = {Free vibration of basalt fiber reinforced polymer ({FRP}) laminated variable thickness plates with intermediate elastic support using finite strip transition matrix ({FSTM}) method},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]W. A. Altabey, “Free vibration of basalt fiber reinforced polymer (FRP) laminated variable thickness plates with intermediate elastic support using finite strip transition matrix (FSTM) method,” Journal of Vibroengineering, vol. 19, no. 4, pp. 2873–2885, Jun. 2017, doi: 10.21595/jve.2017.18154.

Copy IEEE

Copied to clipboard!

Altabey, Wael A. “Free Vibration of Basalt Fiber Reinforced Polymer (FRP) Laminated Variable Thickness Plates with Intermediate Elastic Support Using Finite Strip Transition Matrix (FSTM) Method.” Journal of Vibroengineering 19, no. 4 (June 30, 2017): 2873–85. https://doi.org/10.21595/jve.2017.18154.

Copy Chicago

Copied to clipboard!

Free vibration of basalt fiber reinforced polymer (FRP) laminated variable thickness plates with intermediate elastic support using finite strip transition matrix (FSTM) method

Abstract

1. Introduction

2. Theory and formulation

2.1. Governing equations

2.2. Boundary conditions

2.2.1. Intermediate elastic line support

2.3. Finite strip transition matrix (FSTM) method

3. Results and discussion

3.1. Convergence study and accuracy

3.2. Laminated variable thickness plate with intermediate elastic line support

4. Conclusions

References

Cited by

About this article

Related Articles