Measurement of vibrations of a wing

1. Introduction

In the paper vibrations of a wing are investigated experimentally by using the method of time averaged projection moiré. Experimental setup is developed and the results obtained by using the experimental procedure are analyzed.

Interpretation of projection moiré images on a shallow surface is more complicated than on a plane surface. For this purpose, a special simplified two-dimensional numerical model is developed and used in hybrid experimental – numerical procedures of investigation of vibrations of a wing. This paper continues the analysis of time averaged moiré method presented in [1] and develops optical techniques discussed in [2-13].

2. Experimental measurements of vibrations of a wing

The developed experimental setup for time averaged projection moiré measurement of vibrations is shown in Fig. 1.

General view of the investigated wing is shown in Fig. 2.

Fig. 1The experimental setup

Fig. 2General view of the investigated wing

The investigated wing in the experimental setup is shown in Fig. 3.

Experimental images for three different densities of moiré lines are shown in Fig. 4.

The presented images show that it is important to choose acceptable density of moiré lines for measurement of vibrations.

Fig. 3The investigated wing in the experimental setup

Fig. 4Experimental images for three different densities of moiré lines

a)

b)

c)

3. Simplified two-dimensional model for the analysis of time averaged projection moiré measurement of vibrations

Intensity of the time averaged projection moiré image is represented as:

where $I$ is the intensity of the time averaged projection moiré image, $m$ is a large integer number, $\lambda$ determines the width of moiré lines, $x$ and $y$ are the coordinates of a point of a structure in the status of equilibrium, $d$ is the distance from the grating to the $x$ axis of coordinates, $v$ is the displacement in the direction of the $y$ axis, $\alpha$ is the angle between the direction of incident light and the $y$ axis.

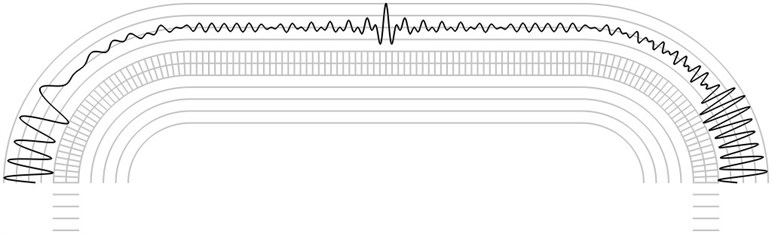
Fig. 5The first eigenmode when a) α=-π/4 and b) α=π/4

a)

b)

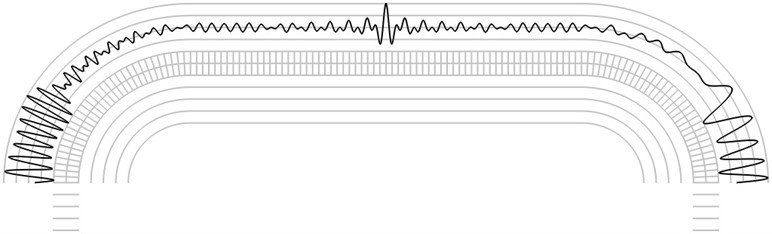
Fig. 6The second eigenmode when a) α=-π/4 and b) α=π/4

a)

b)

Plane strain problem is investigated. The analyzed structure consists of one row of elements located on one fourth of a circle, of a straight part with the length equal to the length of the middle line of half of a circle and of another one fourth of a circle. The following parameters of the investigated structure are assumed: modulus of elasticity $E=\mathrm{}$6·10⁸ Pa, Poisson’s ratio $\nu =$ 0.3, density of the material $\rho =\mathrm{}$785 kg/m³. All displacements of the three nodes on the left end and of the three nodes on the right end are assumed equal to zero.

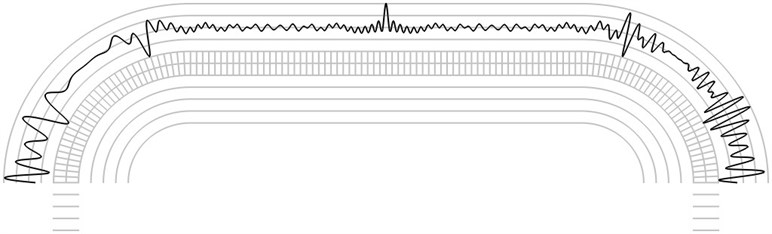
Fig. 7The third eigenmode when a) α=-π/4 and b) α=π/4

a)

b)

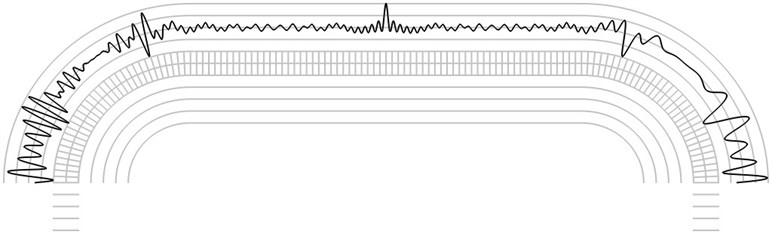
Fig. 8The fourth eigenmode when a) α=-π/4 and b) α=π/4

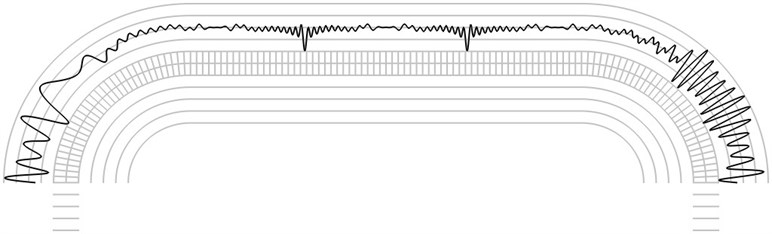
a)

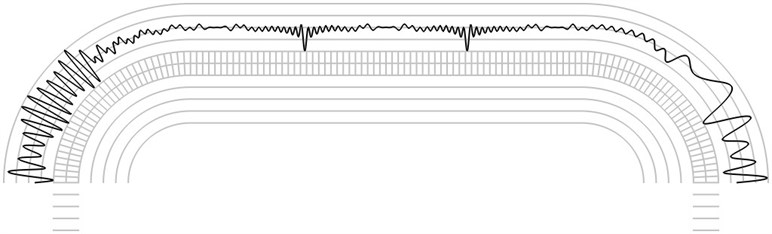
b)

The finite element mesh and lines equidistant in the normal direction to the surfaces of the structure are shown in grey color. Intensity of the time averaged projection moiré images on the upper surface is represented graphically in the normal direction to the surface in black colour. Results are presented for $\alpha =-\pi /4$ and for $\alpha =\pi /4.$ The first eigenmode is shown in Fig. 5, the second eigenmode is shown in Fig. 6, the third eigenmode is shown in Fig. 7 and the fourth eigenmode is shown in Fig. 8.

Graphical relationships of this type are used in hybrid experimental – numerical procedures for interpretation of time averaged projection moiré images on shallow surfaces of wing type. For such surfaces with slow variation of curvature graphical representations of this type are to be investigated for a number of cross sections of the analyzed structure.

4. Conclusions

Vibrations of a wing are investigated experimentally by using the method of time averaged projection moiré. Experimental setup is developed and the results obtained by using the experimental procedure are analyzed.

For interpretation of projection moiré images on a shallow surface a special simplified two-dimensional numerical model is developed and used in hybrid experimental – numerical procedures of investigation of vibrations of a wing. For such surfaces with slow variation of curvature graphical representations of the described type are to be investigated for a number of cross sections of the analyzed structure.