The fuzzy model of the emergency level assessment at sea

Sedova, Nelly A.; Sedov, Viktor A.; Glushkov, Sergey V.

Vibroengineering Procedia

Browse Procedia

Published: 07 October 2016

Check for updates

The fuzzy model of the emergency level assessment at sea

Nelly A. Sedova¹

Viktor A. Sedov²

Sergey V. Glushkov³

^{1, 2, 3}Maritime State University named after G. I. Nevelskoy, Vladivostok, Russian Federation

Corresponding Author:

Viktor A. Sedov

Cite the article Download PDF

Downloads 1358

Abstract

This paper presents the model based on a fuzzy set theory, designed to assess the level of emergency situations at sea. The model consists of three linguistic input variables and one single output. To determine the emergency level at sea, the following was taken into account: information about the dangers to human health and life (group of persons), the extent of damage to the ship and the level of environmental pollution. The paper presents the fuzzy sets corresponding to the term of these linguistic variables and their analytical and graphical representation. The fuzzy product base of fuzzy model contains 80 rules.

1. Introduction

Maritime Safety Committee and Marine Environment Protection Committee by the International Maritime Organization (IMO) in 1997 approved the Provisional Application for Guidelines for Formal Safety Assessment (FSA) for use in the IMO rule-making process. The aim of this concept is to ensure the safe operation of the vessel, including the protection of human life and health, marine environment and property. FSA concept manifests itself in a rational and systematic activities for risk determination related to shipping, and a comparative assessment of the value of variants to reduce those risks. IMO recommends that the FSA as a guide not only for assessment but also for marine security management.

The implementation of the assessment process requires an analysis of emergencies and, therefore, the characteristics of hazards and risks should have a qualitative and quantitative assessment. Assessment of the safety level of navigation is difficult to formalize due to the dependence on numerous factors with complex relationships. The existing probabilistic methods have a major drawback [1]: the same probability of emergencies at sea (SE) leads too different economic and social consequences, which is not recognized in terms of probabilistic methods. The paper [1] offers a “scoring method of emergencies assessment in the maritime transport” which, according to A. Shemelin, is also limited in the ability to form an acceptable universal criterion for assessing the emergency level on the sea.

In this paper we propose a fuzzy model [2-4] of the assessment emergency level at sea, using the point rating method for evaluating emergency level at sea and emergencies classifier presented in [1] and using Mamdani algorithm as a method of fuzzy inference.

2. Description of the fuzzy model of the emergency level assessment at sea

Analyzing the rating method of assessing emergency situations at sea and emergencies classifier presented in [1], the necessary criteria for the formation of the model are defined as follows (Fig. 1): the criterion of health and human life (group of persons) damage, the criterion of ship [5, 6] damage degree and the criterion of environmental pollution.

Fuzzy model of the emergency level assessment at sea has three input and one output linguistic variables (LV) [7-9].

Membership functions of all (and the input and output) linguistic variables were formed using a modified method of assigning parameters and information obtained from a group of four experts in navigation safety. Each expert offers the following information about the parameter: parameter name corresponding to the name of the linguistic variable; range determination parameter corresponding universal set, which specifies the linguistic variable; the number of parameter values corresponding to the term of a linguistic variable; the name of each linguistic term. Each expert was specified the corresponding parameters and the values of each linguistic term core, with the advance pointed out that the core of the internal terms of linguistic variables consists of a single value (for constructing triangular membership functions for internal terms of linguistic variables). Information received from the entire group of experts was averaged.

Fig. 1Basic scheme of the fuzzy model assessment emergency level at sea

The first input LV, which contains the information about causing harm to human health and life (group of people), is determined by the number of injured or dead people and characterized by a basic term-set {single, small, average, large, huge}, the term “single” characterizing sea emergencies with one person killed or missing, or with 5 people who sustained an injury; the term “small” – SE with 2 person killed or missing or more than 5 people injured; the term “average” – SE with 3-4 people killed or missing or more than 10 people injured; the term “large” – SE, with 5 and more people killed or missing or more than 25 people injured; the term “huge” for SE with 10 or more persons killed or missing or more than 50 people injured. Membership functions corresponding to the term of the first input LV are shown in Fig. 2(a), and their analytical view is shown below. A term “single” of the first input LV has a membership function determined by the following formula:

μ_{s i n g l e} (x) = \{\begin{array}{l} 1, \begin{array}{l}  \end{array} x \leq 0,8, \\ \frac{3,5 - x}{2,7}, \begin{array}{l}  \end{array} 0,8 < x < 3,5, \\ 0, \begin{array}{l}  \end{array} 3,5 \leq x . \end{array}

Term “huge” first input LV membership function is determined by the formula:

μ_{h u g e} (x) = \{\begin{array}{l} 0, \begin{array}{l}  \end{array} x \leq 11,5, \\ \frac{x - 0,8}{2,7}, \begin{array}{l}  \end{array} 11,5 < x < 14,2, \\ 1, \begin{array}{l}  \end{array} 14,2 \leq x . \end{array}

The remaining terms of the first input linguistic variable membership functions are defined by the following expressions:

μ_{s m a l l} (x) = \{\begin{array}{l} 0, \begin{array}{l}  \end{array} x \leq 2,5, \\ \frac{x - 2,4}{2}, \begin{array}{l}  \end{array} 2,5 \leq x \leq 4,5, \\ \frac{6,5 - x}{2}, \begin{array}{l}  \end{array} 4,5 \leq x \leq 6,5, \\ 0, \begin{array}{l}  \end{array} 6,5 \leq x, \end{array} μ_{a v e r a g e} (x) = \{\begin{array}{l} 0, \begin{array}{l}  \end{array} x \leq 5,5, \\ \frac{x - 5,5}{2}, \begin{array}{l}  \end{array} 5,5 \leq x \leq 7,5, \\ \frac{9,5 - x}{2}, \begin{array}{l}  \end{array} 7,5 \leq x \leq 9,5, \\ 0, \begin{array}{l}  \end{array} 9,5 \leq x, \end{array}

μ_{l a r g e} (x) = \{\begin{array}{l} 0, \begin{array}{l}  \end{array} x \leq 8,5, \\ \frac{x - 8,5}{2}, \begin{array}{l}  \end{array} 8,5 \leq x \leq 10,5, \\ \frac{12,5 - x}{2}, \begin{array}{l}  \end{array} 10,5 \leq x \leq 12,5, \\ 0, \begin{array}{l}  \end{array} 12,5 \leq x . \end{array}

The second input LV, which contains information about the degree of damage to the ship, consists of the following terms of the basic term-sets (Fig. 2(b)): the term “full” characterizes the emergency situations at sea, resulted in the sinking of the ship or its full constructive destruction and loss of seaworthy condition; term “critical” – SE which resulted in structural damage of the ship with the loss of seaworthiness or the occurrence of any operational constraints; term “average” – when the SE led to damage and restrain of ship operation; term “small” – when the SE led to constructive damage to the hull and didn’t result in the loss of navigability.

Fig. 2Membership functions of linguistic variables: a) in the assessment of damage to life and health of a person (group of persons), b) in the assessment of the ship damage degree, c) in the assessment of the extent of environmental pollution, d) – in the assessment of emergency level at sea

Membership functions of linguistic variables: a) in the assessment of damage to life and health of a person (group of persons), b) in the assessment of the ship damage degree, c) in the assessment of the extent of environmental pollution, d) – in the assessment of emergency level at sea

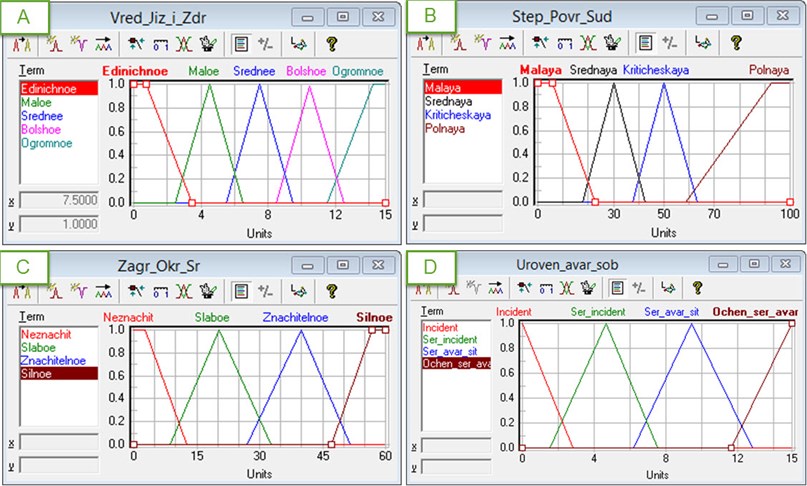
Terms of the basic term-set of the second input linguistic variable of membership functions are defined by the following expressions:

μ_{s m a l l} (x) = \{\begin{array}{l} 1, \begin{array}{l}  \end{array} x \leq 6, \\ \frac{22,7 - x}{16,7}, \begin{array}{l}  \end{array} 6 < x < 22,7, \\ 0, \begin{array}{l}  \end{array} 22,7 \leq x, \end{array} μ_{a v e r a g e} (x) = \{\begin{array}{l} 0, \begin{array}{l}  \end{array} x \leq 17,8, \\ \frac{x - 17,8}{12,2}, \begin{array}{l}  \end{array} 17,8 \leq x \leq 30, \\ \frac{42,6 - x}{12,6}, \begin{array}{l}  \end{array} 30 \leq x \leq 42,6, \\ 0, \begin{array}{l}  \end{array} 42,6 \leq x, \end{array}

μ_{c r i t i c a l} (x) = \{\begin{array}{l} 0, \begin{array}{l}  \end{array} x \leq 37,7, \\ \frac{x - 37,7}{12,3}, \begin{array}{l}  \end{array} 37,7 \leq x \leq 50, \\ \frac{60 - x}{13}, \begin{array}{l}  \end{array} 50 \leq x \leq 63, \\ 0, \begin{array}{l}  \end{array} 63 \leq x, \end{array} μ_{f u l l} (x) = \{\begin{array}{l} 0, \begin{array}{l}  \end{array} x \leq 58,7, \\ \frac{x - 58,7}{34}, \begin{array}{l}  \end{array} 58,7 < x < 92,7, \\ 1, \begin{array}{l}  \end{array} 92,7 \leq x . \end{array}

The third input LV, which tracks the level of environmental pollution, includes the following terms: “insignificant”, “weak”, “significant” and “big”. Term “insignificant” corresponds to the environmental pollution with 0.3 to 1 ton of oil spill; term “weak” – from 1 to 5 tons; term “significant” – from 5 to 50 tons, and the term “big” corresponds to contamination environment in quantities of more than 50 tons. Graphs of the functions of the above terms are shown in Fig. 2(c). The terms of the third input linguistic variable membership functions are defined by the following expressions:

μ_{i n s i g n i f i c a n t} (x) = \{\begin{array}{l} 1, \begin{array}{l}  \end{array} x \leq 2,8, \\ \frac{12,6 - x}{9,8}, \begin{array}{l}  \end{array} 2,8 < x < 12,6, \\ 0, \begin{array}{l}  \end{array} 12,6 \leq x, \end{array} μ_{w e a k} (x) = \{\begin{array}{l} 0, \begin{array}{l}  \end{array} x \leq 8,7, \\ \frac{x - 8,7}{11,3}, \begin{array}{l}  \end{array} 8,7 \leq x \leq 20, \\ \frac{32,8 - x}{12,8}, \begin{array}{l}  \end{array} 20 \leq x \leq 32,8, \\ 0, \begin{array}{l}  \end{array} 32,8 \leq x, \end{array}

μ_{s i g n i f i c a n t} (x) = \{\begin{array}{l} 0, \begin{array}{l}  \end{array} x \leq 27,2, \\ \frac{x - 27,2}{12,8}, \begin{array}{l}  \end{array} 27,2 \leq x \leq 40, \\ \frac{51,3 - x}{11,3}, \begin{array}{l}  \end{array} 40 \leq x \leq 51,3, \\ 0, \begin{array}{l}  \end{array} 51,3 \leq x, \end{array} μ_{b i g} (x) = \{\begin{array}{l} 0, \begin{array}{l}  \end{array} x \leq 47,2, \\ \frac{x - 47,2}{9,8}, \begin{array}{l}  \end{array} 47,2 < x < 57, \\ 1, \begin{array}{l}  \end{array} 57 \leq x . \end{array}

The output linguistic variable corresponds to an emergency level at sea and is characterized by a basic term-set: {incident, serious incident, serious emergency, very serious emergency}. The corresponding membership functions are shown in Fig. 2(d), and terms have membership functions specified by the following formulas:

μ_{i n c i d e n t} (x) = \{\begin{array}{l} \frac{2,8 - x}{2,8}, \begin{array}{l}  \end{array} 0 < x < 2,8, \\ 0, \begin{array}{l}  \end{array} 2,8 \leq x, \end{array} μ_{s e r i o u s i n c i d e n t} (x) = \{\begin{array}{l} 0, \begin{array}{l}  \end{array} x \leq 1,5, \\ \frac{x - 1,5}{3}, \begin{array}{l}  \end{array} 1,5 \leq x \leq 4,5, \\ \frac{7,5 - x}{3}, \begin{array}{l}  \end{array} 4,5 \leq x \leq 7,5, \\ 0, \begin{array}{l}  \end{array} 7,5 \leq x, \end{array}

μ_{s e r i o u s e m e r g e n c y} (x) = \{\begin{array}{l} 0, \begin{array}{l}  \end{array} x \leq 6,5, \\ \frac{x - 6,5}{3}, \begin{array}{l}  \end{array} 6,5 \leq x \leq 9,5, \\ \frac{12,5 - x}{3}, \begin{array}{l}  \end{array} 9,5 \leq x \leq 12,5, \\ 0, \begin{array}{l}  \end{array} 12,5 \leq x, \end{array}

μ_{v e r y s e r i o u s e m e r g e n c y} (x) = \{\begin{array}{l} 0, \begin{array}{l}  \end{array} 11,6 \leq x, \\ \frac{x - 11,6}{3,4}, \begin{array}{l}  \end{array} 11,6 < x < 15 . \end{array}

The set of rules of fuzzy productions of fuzzy model assessment of emergency level at sea consists of 80 items. Implementation of fuzzy model was carried out using FuzzyTECH software. Fig. 3 shows a three-dimensional surface of the fuzzy inference, expressing the dependence of the output LV “The emergency level at sea” on the two input LVs: “degree of damage to the ship” and “harm to human health and life (group of people)”.

Fig. 3Three-dimensional surface of the fuzzy inference

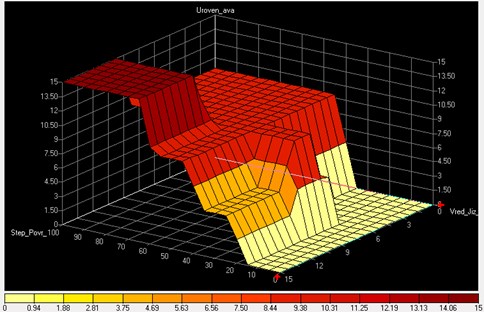
Fig. 4The examples of the functioning of fuzzy model

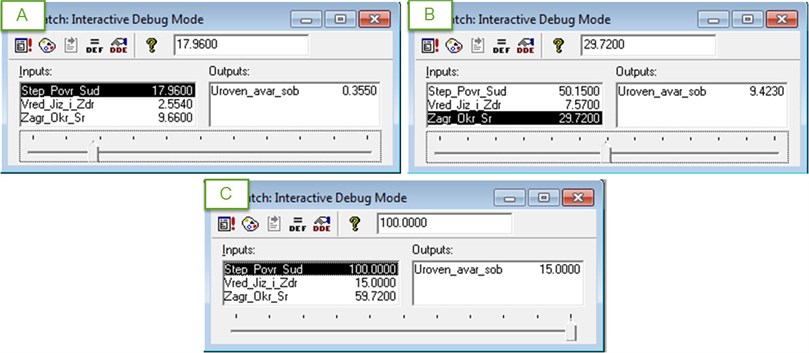
To confirm the efficiency of the fuzzy model we shall review several test cases. The reviewed examples of the fuzzy model functioning are shown in Fig. 4.

Example No. 1. The ship at sea caught in a storm, with several people being injured, small deck equipment damage and a non-significant ejection of fuel barrels overboard by the waves. Entering relevant information, we will obtain a low level emergency at sea, designated by experts as the incident (Fig. 4(a)).

Example No. 2. During the attack on the ship at sea by Somali pirates armed clash occurred as a result 10 people died, the ship was seriously damaged, there was a slight loss of fuel overboard, there was a large oil spill around the ship. Preliminary analysis of this situation defines it as a serious emergency, and the application of fuzzy models makes it possible to calculate the level of emergency resulting in almost 9.4 points out of the maximum 15 (Fig. 4(b)).

Example No. 3. There was a collision between two ships at high speed which led to the complete sinking of one ship, nearly 50 people deaths, a leak from the fuel tank with an oil spill spread over the surface of the sea covering large area. This situation is defined by experts as a very serious emergency, and fuzzy model also determines the emergency level of such situation in 15 points out of 15 (Fig. 4(c)).

Having tested the fuzzy model of assessing the emergency level in different situations at sea, it was considered reliable.

3. Conclusions

The proposed model makes it possible to calculate the emergency level at sea, considering information about the health and life threat, the degree of ship damage and the level of environmental pollution. To describe the model 17 fuzzy sets were introduced, each depicted by a graphical and analytical representation. The base of fuzzy products consists of 80 rules. The test results prove that the model is consistent with the test cases.

References

Shemelin A. V. On the application of quantitative criteria for assessing the emergency level on the sea. Navigation, Vol. 18, 2010, p. 215-223.

Search CrossRef
Bobyr M. V., Titov V. S., Nasser A. A. Automation of the cutting-speed control process based on soft fuzzy logic computing. Journal of Machinery Manufacture and Reliability, Vol. 44, Issue 7, 2015, p. 633-641.

Search CrossRef
Chernova I. V., Sumin S. A., Bobyr M. V., Seregin S. P. Forecasting and diagnosing cardiovascular disease based on inverse fuzzy models. Biomedical Engineering, Vol. 49, Issue 5, 2016, p. 263-267.

Search CrossRef
Luneva E. E., Banokin P. I., Yefremov A. A. Evaluation of social network user sentiments based on fuzzy sets. IOP Conference Series: Materials Science and Engineering, 21st International Conference for Students and Young Scientists, 2015, p. 012054.

Search CrossRef
Antipin A. F. Improving response time of real time control systems based on multidimensional interval-logical controllers. Automation and Remote Control, Vol. 76, Issue 3, 2015, p. 480-486.

Search CrossRef
Chernyi S., Zhilenkov A. Modeling of complex structures for the ship’s power complex using XILINX system. Transport and Telecommunication, Vol. 16, Issue 1, 2015, p. 73-82.

Search CrossRef
Yefremov A. A. New operations on fuzzy numbers and intervals. Proceedings of 2014 International Conference on Mechanical Engineering, Automation and Control Systems, MEACS, 2014, p. 6986900.

Search CrossRef
Nyrkov A. P., Chernyi S. G., Zhilenkov A. A., Sokolov S. S. The use of fuzzy neural structures to increase the reliability of drilling platforms. Proceedings of the 26th International DAAAM Symposium on Intelligent Manufacturing and Automation, 2016, p. 672-677.

Search CrossRef
Antipin A. F. A Computer-aided system for designing multidimensional logic controllers with variables representing a set of binary logic arguments. Automation and Remote Control, Vol. 74, Issue 9, 2013, p. 1573-1581.

Search CrossRef

About this article

Received

06 September 2016

Accepted

12 September 2016

Published

07 October 2016

SUBJECTS

Mathematical models in engineering

Keywords

emergency level

fuzzy set

linguistic variable

term set

fuzzy production rule

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.