Abstract
Traumatic brain injuries (TBI) due to blast-induced wave propagation are not well studied owing to limited published literatures on the subject. This study demonstrates the utilization of a head-helmet model and investigates the effect of using a faceshield with different configurations of laminate composites of polycarbonate and aerogel materials. The model validation is performed against studies published in the literature. The processes of blast wave propagation in the air and blast interaction with the head are modeled by a Coupled Eulerian-Lagrangian (CEL) multi-material finite element method (FEM) formulation, together with a fluid-structure dynamic interaction algorithm. The effectiveness of the different faceshield configurations when exposed to a frontal blast wave with one atmosphere (atm) peak overpressure is evaluated. Results show that the helmet with faceshield can delay the transmission of blast waves to the face and lower the skull stresses and intracranial pressures (ICP) at the frontal and parietal lobes in the first 1.7 ms. Faceshields with a combination of polycarbonate and aerogel layers perform better than the fully polycarbonate ones. It is also revealed that the single 0.6 mm thick aerogel layer in the 3-layer configuration and two layers of 0.6 mm thick aerogel in the 5-layer configuration are the most effective. The paper provides insights into the interaction mechanics between the biological head model and the blast wave.
1. Introduction
The blast-induced TBI is known as the devastating effect to the brain tissue due to the propagating an over pressurized shock wave caused by an explosion. Enormous efforts had been spent in the studies of blast-related injuries with much emphasis on animal tests [1, 2]. Despite of the bulk of useful information provided by these studies, experimental tests on animal living bodies raise many ethic issues and limitations such as controversial experimental results due to extrapolation to conditions of higher severity or even human ones. Moreover, because of the imperfection in in-vivo instrumentation technology, it is little known about in-vivo biomechanical parameters in blast-related TBI (bTBI) and its injury criteria thresholds for human because there is no access to experimental data regarding head-blast interactions. In order to investigate the intracranial blast wave dynamics and to provide some clues about biomechanical responses in bTBI, the finite element method (FEM) was introduced as a cost-effective alternative to the blast injury studies. This in turns led to studies on the possible ways of mitigating the blast effect using personal protective equipments, particularly a helmet. Its first few applications in analyzing the effect of protective helmet on bTBI were reported [3-7]. Grujicic et al. [8] studied the effect of helmet on the blast-induced deformation of the skull using a simplified 3D head and body model, while Ganpule et al. [9] simulated a 1D shock wave towards a 2D head-helmet model. Both studies reported amplified blast pressure concentration in the helmet-head subspace.
Facial protective equipments are proposed to be implemented with combat helmets to minimize this wave-focusing effect as well as to protect the facial structure from penetrating injuries from the blast fragments. To the authors’ best knowledge from the published literature, there are limited computational studies investigating the effect of facial protective equipment in blast injury. The first implementation of a faceshield onto a combat helmet in the event of blast simulation was done by US researchers from the Defense and Veterans Brain Injury Center (DVBIC) in 2010. Moss et al. [10] discovered that nonlethal blasts could induce sufficient skull flexure to generate potentially damaging loads in the brain. More recent ones conducted found that different transparent armour materials such as polycarbonate and laminated glass reduced blast transmission to the face by absorbing and reflecting the pressure away [11-16]. Despite of these studies, there is paucity of information in the literature regarding the further examination of the facial protective gear that could be potentially useful.
Based on the ICP tolerance standard, a harsh brain injury will arise when the vertex ICP goes beyond 235 kPa, while no injuries or minor will arise while the resulting ICP is below 173 kPa [17]. These threshold values are acquired by FE model validation of both animal and human cadaver testing for brain injury [18-20]. A quantity of previous papers on computing method for bio-medical image and numerical head blast simulations correlated with brain injury evaluation [21-24].
There is still a long way to full apprehension of TBI mechanism caused by blast waves, though studies have illustrated that pressure waves may do harm to neural cells. TBI mitigation efforts were concentrated on bringing down the acceleration of the head in TBI studies’ early days [2]. Shock tube experiments that involved temperate animal subjects, nevertheless, implied that primary blast-induced TBIs do occur since TBI was found even in any head motions’ absence [8]. Experimental studies have reported that blast waves may propagate through the cranium of rats [25-27] and through the denser cranium of pigs with a residuary propagating ICP of about two-thirds the incident magnitude [28]. The shockwave transmission at the interface between distinct constitutions like the white-gray substance interface and the solid-fluid interface at the blood-brain barrier likewise reveals a possibility for extra damage [29, 30].
In our study, Numerical analyses of blast-induced waves impacting on the head-helmet model are performed. This study aims to investigate the effectiveness of a faceshield with different configurations in mitigating head injury and to design a facial protective gear that could be potentially useful to military personnel at the frontline. A series of blast simulations have been performed with a finite element model of human head which is equipped with a combat helmet and composed of a faceshield with different configurations, namely single-layered polycarbonate and laminated polycarbonate-aerogel composites. The results obtained from the ICP and skull stress are used in evaluating the effectiveness of each configuration.
2. Methods and materials
2.1. Finite element method (FEM)
In the present study, a total of five transient simulations with different configurations of the helmeted head, subjected to planar blast wave have been carried out using a coupled Eulerian-Lagrangian method (CEL) in Abaqus. This method allows effective modeling of applications involving an extreme deformation such as a fluid flow. The entire head-helmet-cushion-facefield assembly is modeled with Lagrangian elements while the surrounding air which formed the blast environment is modeled with Eulerian elements.
The head model features the main anatomical components of the human head, namely, scalp, skull (cortical bone and trabecular), meninges (dura mater, pia mater, tentorium, falx), cerebrospinal fluid (CSF), cerebrum, cerebellum and neck. The facial features, skull, CSF and brain are modeled with 8-noded hexahedral elements while the neck is meshed with 4-noded tetrahedral elements. The scalp and meninges are created with 4-noded shell elements.
A KELVAR Personnel Armor System Ground Troop (PASGT) helmet is attached to the head with its interior cushioning system which restricts the amount of blast waves from entering the head-helmet subspace. Both the helmet and backrest were modeled using 8-noded brick solid elements whereas the strap and strips were meshed with 4-noded shell elements [10, 30].
As for the faceshield, it is comprised of an aluminum bracket and a 3mm-thick visor. The visor is composed of single-layered polycarbonate or multiple laminates of polycarbonate and aerogel. The entire assembly of the faceshield is responsible for mitigating the effect of the blast front by absorbing some of its energy and diffracting most of the wave away from the vital part of the head, especially the face.
The entire assembly of head-helmet-faceshield is submerged into a cubic blast environment with side length of 330 mm. This Eulerian domain is then meshed using 8-noded hexahedral elements of 3 mm in size and producing a total of 1,331,000 Eulerian elements. Fluid dynamics behavior interacting with the Lagrangian solid model can be captured in a great accuracy.
2.2. Material properties
All of the material properties for the main head-helmet model were assumed to behave as linearly elastic, and isotropic except the helmet which was anisotropic [31]. The helmet was designed to have higher strength and stiffness along the surface contour and normal to it, primarily to stop projectiles effectively. Hence, it was necessary to assign proper material orientation at each element of the helmet in Abaqus.
As for the faceshield assembly, the bracket of the faceshield is made of aluminum, and the visor is made up of a laminate composite of polycarbonate and aerogel, in which the aerogel layer would be sandwiched between the polycarbonate layers. These material properties are obtained from literatures. Table 1 summarizes the material properties assigned to the various components of the simulation model.
Table 1Lagrangian domain material properties
No | Component | Density (kg/mm3) | Young’ s modulus (GPa) | Poisson ratio | Bulk modulus |
Human head assembly | |||||
1 | Cortical bone | 2.00E-06 | 15 | 0.22 | – |
2 | CSF | 1.04E-06 | 0.00015 | 0.499989 | – |
3 | Dura | 1.14E-06 | 0.0315 | 0.45 | – |
4 | Face | 2.50E-06 | 5.54 | 0.22 | – |
5 | Neck (Soft tissue) | 1.06E-06 | 0.11 | 0.45 | – |
6 | Tentorium | 1.14E-06 | 0.0315 | 0.45 | – |
Helmet assembly | |||||
7 | Backrest (Polyurethane) | 1.60E-07 | 0.057 | 0.24 | – |
8 | Helmet | 1.23E-06 | 20/20/7 | 0.33/0.33/0.77 | 0.77/2.715/2.715 |
9 | Inner Strap (Leather) | 1.153E-6 | 0.5 | 0.3 | – |
10 | Strap (Nylon polyester) | 1.16E-06 | 2.4 | 0.35 | – |
11 | Strip (Nylon polyester) | 1.16E-06 | 2.4 | 0.35 | – |
Faceshield assembly | |||||
12 | Bracket (Aluminum) | 2.70E-06 | 70 | 0.35 | – |
13 | Visor (Polycarbonate layer) | 1.22E-06 | 2.4 | 0.37 | – |
14 | Visor (Aerogel layer) | 1.0E-07 | 0.01 | 0.2 | – |
The Eulerian blast environment is filled with air that was modeled using the properties of an ideal gas since the ideal gas model could be used to describe approximately the behavior of real gas, under appropriate conditions such as low pressure and high temperature, based on the Equation of State, written in the form:
where is the ambient pressure, is the gas constant, is the current temperature, and is the absolute zero on the temperature scale being used.
The specific energy depends only on temperature and is given by:
where is initial specific energy at initial temperature, is constant volume heat capacity. The initial ambient temperature of 30 °C and gauge pressure of one atm (103 kPa) is specified in Abaqus and therefore the initial internal volumetric energy of the air can be determined.
2.3. Boundary conditions
For this study, it is assumed that the subject or soldier is directly facing the source of the explosive blast. Non-reflecting Eulerian boundary conditions are applied to all the surfaces of the Eulerian cube encompassing the head helmet model except the frontal surface to simulate an infinite domain. Free inflow condition is applied on these five surfaces such that material can flow into the Eulerian domain freely and the material content and the state of each inflow material are equal to that which originally existed within the element. Such a condition is necessary because the negative pressure phase of the applied pressure of the blast wind is expected to suck air back to the blast source. Thus, any material expelled from cube is needed to return, otherwise, the subsequent negative pressure would produce a higher negative air pressure ambience within the cube which is not accurate and realistic. The five surfaces are also applied with the non-reflecting equilibrium outflow condition that can be used in the unbounded Eulerian domain. As for the Lagrangian solids, a fixity boundary condition is applied at the base of the neck to restrict all the six degrees of freedom of the neck base node.
For the reference scenario, a single planar blast wave is set to impact the face of the head model. The blast pulse is applied to the front Eulerian boundary surface near the face of the head model and simulates a TNT explosion with a resulting peak overpressure of one atm (103 kPa). Due to the source of the blast, a Friedlander waveform with the equation 3 is used.
where denotes the peak pressure and denotes the time duration of the overpressure blast.
2.4. Contact and fluid-structure interaction (FSI)
The interfaces between the head components are of common nodes while that between head and neck is implemented with tie-constraint. Similarly, all the interactions are tied in the helmet-assembly. Additionally, contacts between the helmet-interior cushioning system as well as the interior cushioning system-head are defined by a contact algorithm, which has hard contact pressure-overclosure with default constrain enforcement method.
Interference of the overlapped elements in both the Lagrangian solid model and the Eulerian air domain can result in incorrect prediction of biomechanical parameters such as skull stress and ICP. In order to ensure that two materials (i.e. Eulerian air and any Lagrangian material) will never occupy the same physical space, the Eulerian volume fraction (EVF) tool in Abaqus is used to separate the Eulerian material in the Lagrangian domain, with the Eulerian nodes in the Lagrangian domain assigned with zero velocity. The same method is also used for the nasal and oral cavities (or void) in the model, which would allow the pressure wave to propagate through the face and to enter the cranial cavity, resulting in unrealistic results.
3. Results and discussion
3.1. Intracranial pressures (ICP)
Fig. 1 shows that, without the faceshield, the temporal lobe experiences high ICP at 0.350 ms and the frontal lobe first experiences that at 0.550 ms. It is also observed that the concentration of ICP propagates from the frontal lobe to the occipital lobe between 0.550 and 0.925 ms.
Comparing the cases with and without a faceshield as shown in Fig. 1 and Fig. 2, at 0.350 ms-0.475 ms, the initial high ICP at the temporal lobe for the faceshield case was lower. In addition, comparing the 0.650 ms frame, the ICP at the frontal lobe was significantly reduced. However, for the case with faceshield, at 1.900 ms-1.975 ms, high ICPs were observed at the frontal and temporal lobe. This was probably due to the trapped air that was accumulated and reflected to and for between the face and the faceshield.
Fig. 1ICP contour of model without faceshield
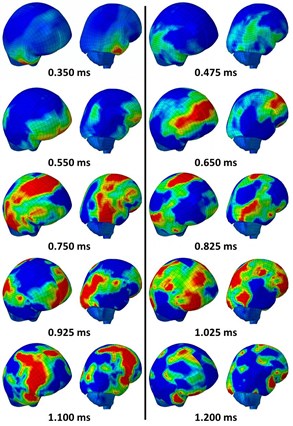
Fig. 2ICP contour of model with faceshield
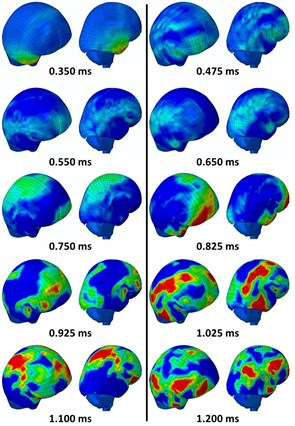
Fig. 3Intracranial pressure at frontal lobe with and without faceshield
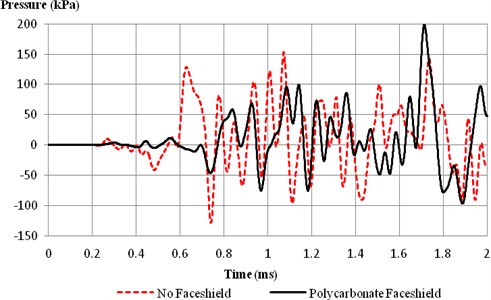
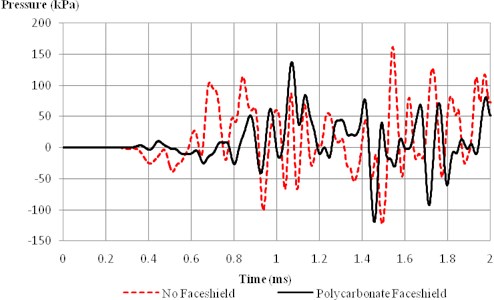
Fig. 3 and Fig. 4 shows the ICP history plots of model with and without faceshield at frontal and parietal lobes and shows the ICP reaches an initial peak of 122 kPa at around 0.62 ms without faceshield. Subsequently, the ICP of both the frontal and parietal lobes fluctuates throughout the entire simulation. It is also noted that the blast wave takes 0.08 ms to reach the posterior brain from the anterior as observed in the ICP contour plots, time delay in the initial peak positive pressure is also seen in both plots.
Fig. 4Intracranial pressure at parietal lobe with and without faceshield
3.2. Skull stress
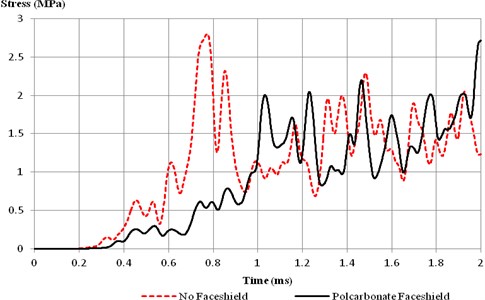
In terms of stress propagation in Fig. 5 and Fig. 6, both cases indicated the similarity in the direction of propagation and its intensity. But the faceshield case appeared to register a reduction in stress at the side of the skull.
Fig. 5Skull stress at front point with and without faceshield
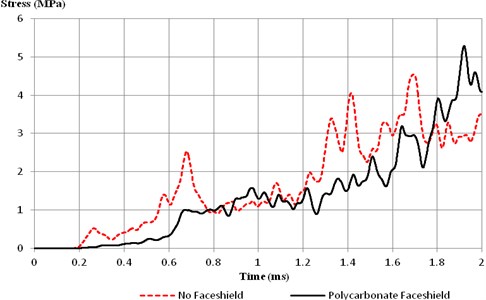
Fig. 6Skull stress at top point with and without faceshield
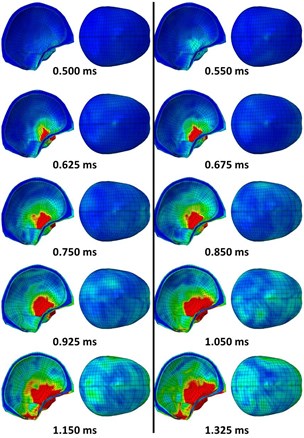
The skull stress propagated from the front section of the skull to the back at 0.500 ms-1.050 ms (Fig. 7 and Fig. 8) and then due to the air that was sucked in, propagated back to the front again at 1.150 ms. The high stress region occurred at the side of the skull, which began from the bottom front and ended at the bottom end.
Fig. 7Skull stress contour model without faceshield
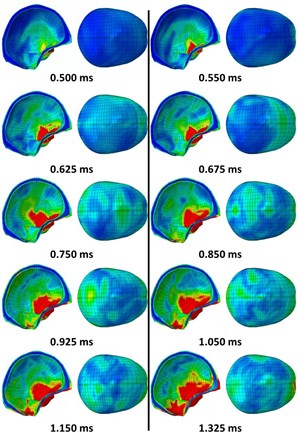
Fig. 8Skull stress contour model with faceshield
For both locations of skull (cranium), the lower stresses at the initial peak of faceshield model when compared to the no faceshield case suggested that the faceshield was able to mitigate the blast effect to the skull by diffracting the wave away. But it could be seen in the faceshield case, the maximum stress was higher at the front point and maximum stresses at both points occurred at the later part of the run, at 1.91 ms onwards. This was probably due to accumulated air pressure between the faceshield and face.
3.3. Evaluation on different faceshield configuration
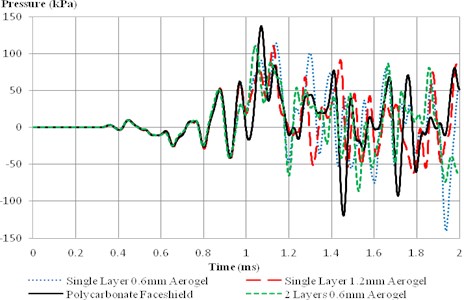
From the plots in Fig. 9 and Fig. 10, it was observed that the exact same pulse was shared by all configurations until after 0.9 ms. At this time, the blast front had passed the head and negative phase of the blast began to suck the pressure back. From Table 2, the fully polycarbonate faceshield (no aerogel) delayed the high ICP but eventually resulted in higher ICP at the frontal lobe. Next, single layer 0.6 mm aerogel faceshield seemed to perform better than the single layer 1.2 mm aerogel one. But when the single layer 1.2mm aerogel were split into two layers of 0.6 mm and arranged as a 5-layer configuration, the faceshield performed better at mitigating the blast effect.
Table 2ICP at frontal lobe for different faceshield configurations
ICP at frontal lobe | Max pressure (kPa) | Time (ms) | Min pressure (kPa) | Time (ms) |
Polycarbonate faceshield | 194 | 1.71 | –85 | 1.87 |
Single layer 0.6 mm aerogel | 159 | 1.23 | –132 | 1.88 |
Single layer 1.2 mm aerogel | 201 | 1.37 | –154 | 1.55 |
Two layers 0.6 mm aerogel | 110 | 1.09 | –135 | 1.88 |
The same phenomena that occurred at ICP took place at the skull points. Thinner aerogel layer (0.6 mm aerogel) mitigated the blast effect at the front point better whereas thicker aerogel layer (1.2 mm aerogel) reduced the blast effect at the top point better. In terms of mitigating the blast effect at front point, the two layers of 0.6 mm aerogel performed the best whereas a single 1.2 mm aerogel mitigated the blast effect the most.
Fig. 9Intracranial pressure at frontal lobe for different faceshield configurations
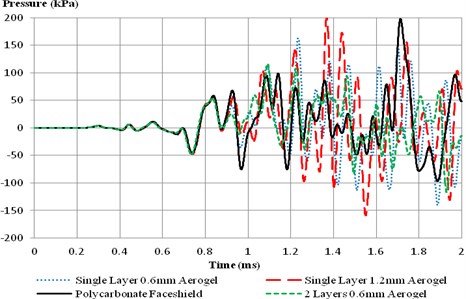
Fig. 10Intracranial pressure at parietal lobe for different faceshield configurations
3.4. Discussion
The primary mode of comparison to be used against other research works to validate the results that had been obtained was to compare 1) the range of peak values of ICP and 2) the maximum values of skull stress.
The ICP range of the frontal lobe and parietal lobe was observed to be at –119 to 154 kPa and –119 to 161 kPa respectively. Based on Grujicic et al. [8] in their work on 0.1 MPa (1 atm) peak overpressure TNT blast, the ICP values registered to their head helmet model were between –80 kPa and 80 kPa. Another work by Zhang et al. [32] obtained peak ICP values of 600 kPa from 0.27 MPa (2.7 atm) peak overpressure TNT blast for the helmeted case.
In this work, the skull stress of the front point and top point was observed to be at 4.37 MPa and 2.71 MPa respectively. In the work of Courtney et al. [13] which involved TNT-based 0.1 MPa peak overpressure, their simulation results obtained skull stress Mises value of about 6 and 11 MPa for two different helmet configuration cases.
In the literature study, it has been observed that slight differences in the geometry of a head model, the configuration of the helmet and its interior pad system and also the material properties given to the components produced different results in ICP and skull stress values [10]. Since the values obtained in this work on the model without faceshield were in the same order as those published, the model that had been used was justified in terms of accuracy and could be used for future works.
4. Conclusions
1) The utilization of a head-helmet model for blast wave impact simulations using Abaqus has been demonstrated. The single frontal blast simulation is conducted by applying CEL method. The effectiveness of the different faceshield configurations is evaluated, and a combination of polycarbonate and aerogel layers performs better than the fully polycarbonate case at mitigating the ICP at the frontal and parietal lobe.
2) It is found that better mitigating effect can be acquired at the parietal lobe and two skull points by increasing the aerogel thickness in the 3-layer configuration faceshield. In addition, the 5-layer faceshield configuration is the most effective in blast mitigation at frontal lobe, parietal lobe and the frontal section of the skull.
3) The results of the head-helmet model without faceshield were validated against other simulated works by comparing the ICP values obtained. Even though the ICP values are different, they are still in the same order and the difference among the works. This is due to different head-helmet model and material properties used. Hence, this model could be used to predict the blast results of future work.
References
-
Gruss E. A correction for primary blast injury criteria. The Journal of Trauma Injury, Vol. 60, Issue 6, 2006, p. 1284-1289.
-
Taber K. H., Warden D. L., Hurley R. A. Blast-related traumatic brain injury: what is known? Journal of Psychiatry and Neuroscience, Vol. 18, Issue 2, 2006, p. 141-145.
-
Chen Y. C., Smith D. H., Meaney D. F. In-vitro approaches for studying blast-induced traumatic brain injury. Journal of Neurotrauma, Vol. 26, Issue 6, 2009, p. 861-876.
-
Zhang D. G., Kang X. J. A new SC-based method of non-line wavelet shrinkage denoising. Information – An International Interdisciplinary Journal, Vol. 15, Issue 1, 2012, p. 141-148.
-
Ma Z., Zhang D. G., Chen J. Shadow detection of moving objects based on multisource information in internet of things. Journal of Experimental and Theoretical Artificial Intelligence, Vol. 28, Issue 3, 2016, p. 253-265.
-
Zhang D. G., Wang X., Song X. D. A novel approach to mapped correlation of ID for RFID anti-collision. IEEE Transactions on Services Computing, Vol. 7, Issue 4, 2014, p. 741-748.
-
Ma Z., Zhang D. G., Liu S., Hou Y. X. A novel compressive sensing method based on SVD sparse random measurement matrix in wireless sensor network. Engineering Computations, Vol. 33, Issue 8, 2016, p. 2448-2462.
-
Grujicic M., Bell W. C., Pandurangan B., Glomski P. S. Fluid/structure interaction computational investigation of blast-wave mitigation efficacy of the advanced combat helmet. Journal of Materials Engineering and Performance, Vol. 20, Issue 6, 2011, p. 877-893.
-
Ganpule S., Gu L., Gao G., Chandra N. The effect of shock wave on a human head. ASME International Mechanical Engineering Congress and Exposition, 2009, p. 339-346.
-
Moss W. C., King M. J., Blackman E. G. Skull flexure from blast waves: a mechanism for brain injury with implications for helmet design. Physics Review Letter, Vol. 103, Issue 10, 2009, p. 108702.
-
Zhang D. G., Liang Y. P. A kind of novel method of service-aware computing for uncertain mobile applications. Mathematical and Computer Modelling, Vol. 57, Issues 3-4, 2013, p. 344-356.
-
Zhang D. G., Song X. D., Wang X. New agent-based proactive migration method and system for big data environment (BDE). Engineering Computations, Vol. 32, Issue 8, 2015, p. 2443-2466.
-
Courtney E. D., Courtney A. C., Courtney M. W. Blast wave transmission through transparent armour materials. Journal of Battlefield Technology, Vol. 15, Issue 2, 2012, p. 19-22.
-
Zhang D. G., Zhang X. D. Design and implementation of embedded un-interruptible power supply system (EUPSS) for web-based mobile application. Enterprise Information Systems, Vol. 6, Issue 4, 2012, p. 473-489.
-
Zhang D. G. A new approach and system for attentive mobile learning based on seamless migration. Applied Intelligence, Vol. 36, Issue 1, 2012, p. 75-89.
-
Zhang D. G., Li G., Zheng K. An energy-balanced routing method based on forward-aware factor for wireless sensor network. IEEE Transactions on Industrial Informatics, Vol. 10, Issue 1, 2014, p. 766-773.
-
Lockhart P. A. Primary Blast of the Head: Numerical Prediction and Evaluation of Protection. Mechanical and Mechatronics Engineering, University of Waterloo, Waterloo, 2010.
-
Zhang D. G., Li W. B., Liu S., Zhang X. D. Novel fusion computing method for bio-medical image of WSN based on spherical coordinate. Journal of Vibroengineering, Vol. 18, Issue 1, 2016, p. 522-538.
-
Zhang D. G., Zheng K., Zhang T. A novel multicast routing method with minimum transmission for WSN of cloud computing service. Soft Computing, Vol. 19, Issue 7, 2015, p. 1817-1827.
-
Chafi M., Karami G., Ziejewski M. Biomechanical assessment of brain dynamic responses due to blast pressure waves. Annals of Biomedical Engineering, Vol. 38, Issue 2, 2010, p. 490-504.
-
Zhang D. G., Kang X. J. A novel image de-noising method based on spherical coordinates system. EURASIP Journal on Advances in Signal Processing, Vol. 110, Issue 2012, 2012, p. 1-10.
-
Zhang D. G., Song X. D., Wang X. New medical image fusion approach with coding based on SCD in wireless sensor network. Journal of Electrical Engineering and Technology, Vol. 10, Issue 6, 2015, p. 709-718.
-
Zhang D. G., Zheng K., Zhao D. X. Novel quick start (QS) method for optimization of TCP. Wireless Networks, Vol. 22, Issue 1, 2016, p. 211-222.
-
Chavko M., Koller W. A., Prusaczyk W. K., McCarron R. M. Measurement of blast wave by a miniature fiber optic pressure transducer in the rat brain. Journal of Neuroscienes Methods, Vol. 159, Issue 2, 2007, p. 277-281.
-
Zhang D. G., Zhao C. P. A new medium access control protocol based on perceived data reliability and spatial correlation in wireless sensor network. Computers and Electrical Engineering, Vol. 38, Issue 3, 2012, p. 694-702.
-
Krave U., Hojer S., Hansson H. A. Transient powerful pressures are generated in the brain by a rotational acceleration impulse to the head. European Journal of Neurosciene, Vol. 21, Issue 10, 2005, p. 2876-2882.
-
Zhang D. G., Zhu Y. N. A new constructing approach for a weighted topology of wireless sensor networks based on local-world theory for the Internet of Things (IOT). Computers and Mathematics with Applications, Vol. 64, Issue 5, 2012, p. 1044-1055.
-
Chen Y. C., Smith D. H., Meaney D. F. In-vitro approaches for studying blast-induced traumatic brain injury. Journal of Neurotrauma, Vol. 26, Issue 6, 2009, p. 861-876.
-
Zhao D., Ang L., Ji C. Z. Numerical and experimental investigation of the acoustic damping effect of single-layer perforated liners with joint bias-grazing flow. Journal of Sound and Vibration, Vol. 342, 2015, p. 152-167.
-
Lee H. P., Gong S. W. Finite element analysis for the evaluation of protective functions of helmets against ballistic impact. Computer Methods in Biomechanics and Biomedical, Vol. 13, Issue 5, 2010, p. 537-550.
-
Yang B., Tse K. M., Chen N., et al. Development of a finite element head model for the study of impact head injury. Biomed Research International, Vol. 2014, 2014, https://doi.org/10.1155/2014/408278.
-
Zhang L. Y., Makwana R., Sharma S. Comparison of the Head Response in Blast Insult with and Without Combat Helmet. Report for USADOD. W81XWH-08-1-0678 (LYZ), Wayne State University, NATO-OTAN, RTO-MP-HFM-207.
About this article
The financial supports from the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20161522, BK20130977), the National Natural Science Foundation of China (Grant No. 61403204), the State Laboratory of Advanced Design and Manufacturing for Vehicle Body (Grant No. 31415008), Six Talent Peaks Project in Jiangsu Province, China (Grant No. JXQC-023) and Chinese Postdoctoral Science Foundation (Grant No. 2015M572243).
All authors were involved in the study. Li and Shi co-conceived and co-developed the FE model for the manuscript. Tang co-conceived and co-developed the idea, and facilitated the gathering of contributors. Yang initiated the project, co-developed and co-refined the intellectual content, and wrote the first two drafts. Wang Yu co-developed the idea, edited all drafts. Wang Qun co-developed the idea and conducted the keyword search. Cao is the guarantor for the integrity of the article as a whole.
