Research on unbalance vibration signal de-noising of motorized spindle

1. Introduction

In CNC machine tools, the performance of motorized spindle largely determines the performance and the development level of the CNC machine tools, such as precision, stability, range of applications [1]. With the development of high-end CNC machine in the direction of high speed and high precision, unbalance vibration caused by the operation of the machine became the bottleneck problem which restricted the operation precision of spindle and the processing quality and cutting capacity of the CNC machining [2]. As the core technology to control unbalance vibration, the active balancing technology is more and more important in the field of the motorized spindle unit technology. In the research of the technology, to get accurate and reliable unbalanced signal is a prerequisite to achieve high-precision active balancing [3].

According to the analysis of rotor dynamics, the unbalanced signal is a sinusoidal signal with the same frequency of rotor speed [4]. However, due to the mechanical and electrical interference, the original vibration response signal obtained from the sensor has the following two characteristics: one is that the signal is low signal to noise ratio (SNR) and with strong near-frequency interference, the other is that the signal is non-stationary and time-varying, and the speed fluctuation usually causes the change of interfering frequency [5]. Therefore, probing useful signal processing method to accurately extract the most sensitive unbalance signal from the low SNR, non-stationary vibration signal, which can suppress noise and interference signals as far as possible and meet the high precision requirements of the active balancing of the motorized spindle, has become an important research hotspot in recent years [6].

The time-frequency analysis methods which can describe the time-frequency localization characteristic of the non-linear and non-stationary signal, such as time series forecasting [7], order tracking analysis theory [8-9], and Hilbert-huang transform which has excellent harmonic decomposition capability [10] became the research hotspot in this field and scholars accumulated fruitful achievement. David Coats et al. put forward an advanced time-frequency mutual information measures for condition-based maintenance of helicopter drivetrains [11]. Raj and Murali used morphological operators and fuzzy inference to early classification of bearing faults [12]. Beltran et al. researched on active unbalance control of rotor systems using on-line algebraic identification methods [13]. Chen et al. used wavelet transform and power spectral density to extract the unbalance features of spindle system [14].

However, when these methods are used to process the low SNR and time-varying vibration signal, it is easy to lose part of useful unbalance signal in the meanwhile of removing the noise. For example, the wavelet analysis method has the problem of frequency aliasing during the signal decomposition and reconstruction process. In other words, the new frequency none of the original signal frequency will generate, which will generate new noise interference and hinder the improvement of SNR. In the study of lifting wavelet, the authors found that the adaptive redundant lifting wavelet can suppress the frequency aliasing and has the characteristic of translation invariance in time domain [15]. So the application of adaptive redundant lifting wavelet in the vibration signal of low SNR has a good de-noising effect.

Although the adaptive redundant lifting wavelet can effectively suppress the frequency aliasing, the threshold processing of signal de-noising is flawed. Since the approximation signal is different on different scales, when the wavelet function and the local feature of the approximation signal on each scale can’t be matched well, the smaller detail signal will generate. In the threshold processing large amounts of detail signal are filtered as noise, so that the de-noising signal loses part of useful information. Taking the commonly used soft threshold function for example, although the continuity of de-noising wavelet coefficients using soft threshold function is better, there is certain deviation compared with the real wavelet coefficients. The precision of the reconstruction signal is poor [16].

In view of the above questions, a signal de-noising method combined adaptive redundancy lifting wavelet with bivariate improved threshold function was put forward in this paper. Through the engineering verification, the effect of signal de-noising using different threshold function with variable parameter was compared and analysed. The results verified that the bivariate improved threshold function based on adaptive redundancy lifting wavelet could improve the de-noising effect of the unbalance vibration signal.

2. Unbalance signal de-noising model of motorized spindle

2.1. Vibration signal model in active balancing

Online active balancing system of motorized spindle is a faulty self-healing control system, putting real-time monitoring, active control technology and intelligent fault diagnosis as a whole. It is composed of three parts: the actuator (balancing head), the sensors, and the controller, shown in Fig. 1. Over the entire speed range of motorized spindle, the vibration sensors installed in the seat gathered the vibration signal of the motorized spindle in real time. Once the vibration caused by unbalance exceeded the warning value, the system will take unbalance compensation measures in order to achieve self-balancing in case of non-stop. Fig. 2 showed the motorized spindle installed the balancing head.

According to the different features and sources, the unbalance vibration signal could be divided into the following parts:

1) The unbalance signal, that is the sinusoidal signal with the same frequency of rotating speed of motorized spindle, i.e. the fundamental frequency component, expressed as $E\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t+\phi \right)$, of which $E$ is the amplitude of the unbalance signal, $\phi$ is the initial phase of unbalance signal, $\omega$ is the angular frequency of working speed;

2) The harmonic interference of unbalance signal, expressed as $\sum _{i=2}^n{E}_i\mathrm{s}\mathrm{i}\mathrm{n}(i\omega t+\phi )$;

3) The tiny DC component in vibration signal caused by zero drift because of the instability of an external system, expressed as $E_0$;

4) The white noise generated by electronic components in the system and the interference due to casual factors of external environmental, expressed as $n\left(t\right)$.

Therefore, the vibration signal of online active balancing can be expressed as:

1

$e\left(t\right)=E_0+E\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t+\phi \right)+\sum _{i=2}^n{E}_i\mathrm{s}\mathrm{i}\mathrm{n}(i\omega t+\phi )+n\left(t\right).$

The de-noising goal is to obtain the phase and amplitude of the unbalance signal from the vibration signal.

Fig. 1Active balancing system of motorized spindle

a) The physical photo

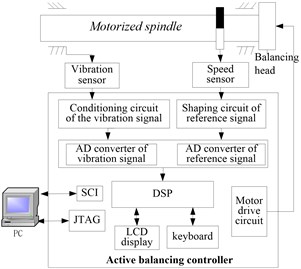
b) System architecture diagram

Fig. 2The motorized spindle with the balancing head

2.2. The unbalance signal de-noising method

2.2.1. Principle of adaptive redundant lifting wavelet transform

In order to overcome the frequency aliasing of the signal in split and synthesis procedure of the lifting wavelet transform, the adaptive redundant lifting wavelet cancelled the split procedure in the decomposition process and the synthesis procedure in reconstruction process. That is to say it does not perform the sampling algorithm. The length of the approximation signal and detail signal is the same as the original signal and the information is redundant. Therefore, more abundant characteristic information and more accurate frequency localization information can be provided. Besides the solution of the lifting wavelet in which the prediction procedure is before the update procedure, easily lead to the complex calculation of the updater. So a new method that the update procedure is before the prediction procedure in the decomposition process is proposed in this paper, which makes the predictor without the loop of cascaded iteration operation, namely the approximate coefficient was not affected by nonlinear predictor. Thus the accumulation error in cascaded error can be reduced.

The original signal sequence is hypothesized as $x=\left(x_i\right)$, $i=$ 0, 1,…, $l$, $L$ is the data length. The decomposition process of adaptive redundancy lifting wavelet transform can be shown as follows:

1) Update: the purpose of the update is to find a better subset of approximate coefficients $a_k$, so that it could remain a global property of the input signal sequence $a_{k-1}$. The expression of the update step is:

2

$a_k\left(n\right)=a_{k-1}\left(n\right)+\sum _{j=1}^{N_k}{u}_u^k\left(j\right)d_k(n-N_d+j-2),$

where $a_k$ is the approximate coefficients of the decomposition process on the $k$ layer. $U_U^k$ is redundant updater of decomposition process on the $k$ layer. $N_k$ is the length of the redundant updater coefficient. $U_U^k$ can be obtained by interpolating zero on the basis of the initial updater.

2) Structure adaptive updater: the adaptive updater $U_{ssy}(\bullet )$ will be structured when the information entropy of objective function $P\left(w\right)=\sum _j{\left|w_j\right|}^2\mathrm{l}\mathrm{o}\mathrm{g}{\left|w_j\right|}^2$ is minimum. $w_j$ is the approximate coefficient $a_k$ obtained by step 1.

3) Adaptive update: repeat step 2 to generate the adaptive approximate coefficient $a_k$ using the adaptive updater $U_{ssy}(\bullet )$ obtained by step 2.

4) Prediction: the purpose of prediction is to eliminate the redundancy after splitting and give a more compact expression of data. The detail coefficients $d_k$ were obtained by using redundant predictor $P_U^k$ whose initial predictor has different length to act on the approximate coefficients $a_k$. The formula is as follows:

3

$d_k\left(n\right)=a_{k-1}\left(n\right)-\sum _{i=1}^{M_k}{p}_u^k\left(i\right)a_k\left(n-M_d+i-1\right),$

where $P_U^k$ is obtained by interpolating zero on the basis of the initial predictor. $M_k$ is the length of the redundant predictor coefficient.

5) Structure adaptive predictor: the adaptive predictor $P_{ssy}(\bullet )$ will be structured when the information entropy of objective function $P\left(w\right)=\sum _j{\left|w_j\right|}^2\mathrm{l}\mathrm{o}\mathrm{g}{\left|w_j\right|}^2$ is minimum. $w_j$ is the detail coefficients $d_k$ obtained in step 4.

6) Adaptive predict: repeat step 5 to generate the adaptive detail coefficient $d_k$ using the adaptive predictor $P_{ssy}(\bullet )$ obtained in step 5.

Fig. 3Adaptive redundant lifting wavelet transform

Because the lifting wavelet transform is completed in the time domain, the reconstruction process can be realized through the reverse direction of signal flow and the reverse operator of the original formulas in the decomposition process. In other words the reconstruction process includes recovery prediction, recovery update, and then averaging these results to merge. Adaptive redundant lifting wavelet transform process is shown in Fig. 3.

2.2.2. Improved adaptive redundant lifting wavelet de-noising algorithm

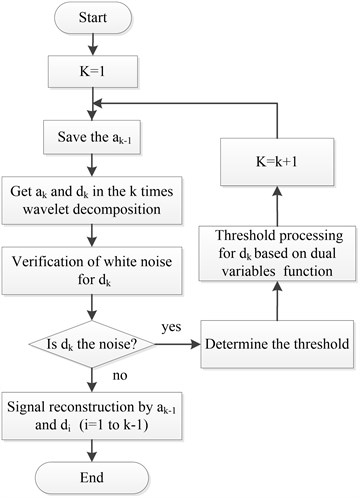
In the signal de-noising method based on adaptive redundant lifting wavelet, the bivariate improved threshold function was brought in the threshold processing to solve the feature extraction of unbalance signal. The algorithm flow was shown in Fig. 4.

First the detail coefficient $d_k$ and approximate coefficient $a_k$ were calculated by wavelet decomposition for the vibration signal. Then the time series method was used for verification of the detail coefficient $d_k$, to judge whether it was noised sequence or not. If so, the optimal threshold selection method was chosen to determine the threshold of detail coefficient $d_k$ for each scale, then the bivariate threshold function was used for threshold processing of the signal. Continue to decompose a signal until $d_k$ is not noise sequence. Through the wavelet reconstruction using the detail coefficient of each layer and the approximate coefficient of the last layer, the de-noising signal can be obtained.

Fig. 4The algorithm flow of improved adaptive redundancy lifting wavelet de-noising method

2.2.3. The method of threshold processing

The threshold processing involves the rules of threshold selection and the selection of threshold functions. In other words, the first procedure is to determine the threshold of each layer in the wavelet decomposition process, according to the appropriate threshold selection algorithm. The next procedure is to process the detail coefficients of each scale according to threshold function. So the quality of threshold function and threshold selecting method directly affects the effect of signal de-noising. It is the key issue in threshold processing. However, the traditional soft and hard threshold function has respective potential deficiencies. Because of its continuity, the bivariate improved threshold function proposed by this paper could avoid oscillation which hard threshold function maybe cause. By adjusting the parameters, it also could overcome coefficient deviation question which soft threshold function caused.

There are many selection schemes of threshold. Considering the propagation characteristics of the detail coefficients of noise in the wavelet domain, a threshold selection scheme was chosen in this paper as following:

4

$t_k=m{\sigma }_k,$

where ${\sigma }_k$ is the standard deviation of detail signal $\left|d_k\right|$ at $k$ layer. The coefficient $m$ is manually determined on the different signal and noise. From the equation, we can see that the threshold in every layer is not only related to the standard deviation of detail coefficient, but also can be changed manually by the adjustment of coefficient m on the basis of the actual situation, so that we can get better threshold.

Traditional threshold function included hard and soft threshold function. Hard threshold function only remains the values which the absolute value of the wavelet coefficient is equal to or greater than the threshold value $\lambda$ set in advance, and the remained wavelet coefficient is same as the original coefficient. Meanwhile the values which are less than the threshold value $\lambda$ were set to zero. The formula of hard threshold function is as follows:

5

${\widehat{\omega }}_{j,k}=\left\{\begin{array}{ll}0,& {|\omega }_{j,k}|<\lambda ,\\ {\omega }_{j,k},& {|\omega }_{j,k}|\ge \lambda .\end{array}\right.$

In soft threshold function, the absolute value of the wavelet coefficient which is equal to or greater than the threshold value $\lambda$ set in advance is contracted by $\lambda$, and the values which less than threshold value $\lambda$ were set to zero. The formula of soft threshold function is as follows:

6

${\widehat{\omega }}_{j,k}=\left\{\begin{array}{ll}0,& {|\omega }_{j,k}|<\lambda ,\\ {\mathrm{s}\mathrm{g}\mathrm{n}(\omega }_{j,k}\left)\right({|\omega }_{j,k}|-\lambda ),& {\omega }_{j,k}\ge \lambda .\end{array}\right.$

The bivariate improved threshold is developed on the basis of the traditional threshold function. The formula is as follows:

7

${\widehat{\omega }}_{j,k}=\left\{\begin{array}{ll}{\omega }_{j,k}+\lambda -i\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left({nT}^{2m+1}\right),& {\omega }_{j,k}\le \lambda ,\\ i\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left({nT}^{2m+1}\right),& {|\omega }_{j,k}|<\lambda ,\\ {\omega }_{j,k}-\lambda +i\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left({nT}^{2m+1}\right),& {\omega }_{j,k}\ge \lambda .\end{array}\right.$

The Eq. (7) must meet the constraint conditions of Eqs. (8), (9) [23]:

8

$n=\frac{2m+1+\sqrt{{\left(2m+1\right)}^2-{\pi }^2}}{\pi {\lambda }^{2m+1}},$

9

$i=\frac{1+{\left(n{\lambda }^{2m+1}\right)}^2}{\left(2m+1\right)n{\lambda }^{2m}},$

and $m>\mathrm{}$0, and $m$ is an integer.

In above formulas, ${\widehat{\omega }}_{j,k}$ is the wavelet coefficient after threshold processing. ${\omega }_{j,k}$ is the wavelet coefficient with the noise. $\lambda$ is the threshold variable. $m$ and $n$ are variable parameters. The bivariate improved threshold function has continuous first-order derivatives, which has a smooth transition region between the useful signal and noise. Thereby the change of two parameters would directly affect the de-noising effect. We focused on the value of the two variable parameters in this part, and ultimately selected the parameter value which could get the best de-noising effect.

3. Engineering verification and discussion

In order to verify the de-noising effect of our method, the experimental platform shown in Fig. 5 was set up, including motorized spindle, inverter, oil and gas lubrication system, vibration measuring instrument DZ-2, the vibration sensors installed at both ends of the motorized spindle and the signal analyzer. The model number of the experimental motorized spindle was 150MD24Y16 from a company, with a known mass unbalance and phase. The vibration signal of motorized spindle gathering from the platform was an unbalance vibration signal with noise.

10240 sampling points were taken from the acquisition of the vibration signal. Sampling frequency was 8000 Hz. The time-domain graph of the original vibration signal is shown in Fig. 6(a). The de-noising experiments of the vibration signal using improved adaptive redundancy lifting wavelet were simulated in Matlab. Two variable values of the bivariate threshold function were respectively $m=$ 2, $n=$ 0.5. Fig. 6(b) was the time domain graph of de-noising signal using bivariate threshold functions. Fig. 6(c) and Fig. 6(d) were respectively the time domain graph of de-noising signal using hard threshold function and soft threshold function.

Fig. 5Active balancing experiment platform of motorized spindle

a) The motorized spindle used oil and gas lubricating system during operation

b) Motorized spindle was driven by inverter

Fig. 6Time domain graph of original vibration signal and de-noising signal using adaptive redundant lifting wavelet

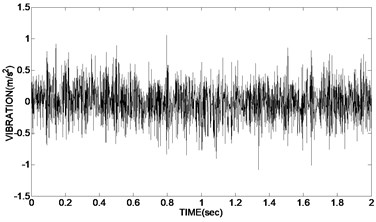
a) The original vibration signal

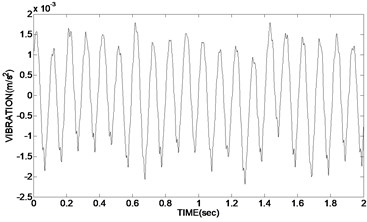
b) Using bivariate threshold function

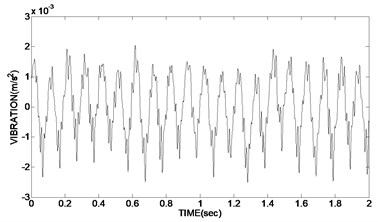
c) Using hard threshold function

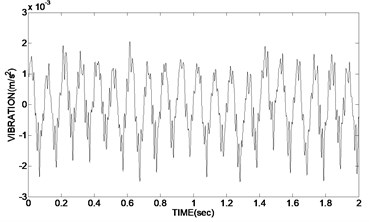
d) Using soft threshold functions

To verify the results of engineering applications, the time domain graph of de-noising signal was transformed into frequency domain graph, and the amplitude and phase of the unbalance signal was extracted. Fig. 7(a) showed the frequency domain graph of the original vibration signal. The frequency domain graph of the de-noising signal using bivariate threshold function, the hard threshold function and the soft threshold function based on adaptive redundant lifting wavelet were shown in Fig. 7(b)-(d).

As can be seen from the experimental results, the time-domain diagram of Fig. 6(b) is clearly more regularity than Fig. 6(c) and Fig. 6(d). In Fig. 6(c) the de-noising waveforms using hard threshold existed oscillation, and the effect of de-noising is not very obvious; although in Fig. 6(d) the de-noising waveforms using soft threshold is relatively smooth, the reconstruction precision of the signal is not high, which has a deviation with the real signal and a low SNR; instead in Fig. 6(b) the de-noising waveform using double variables improved threshold function is smooth and without oscillation. The reconstruction precision is high. Meanwhile the two variable of the improved function is easy to adjust and use.

The results of Fig. 7(b) showed that the proposed de-noising method in the paper can further reserve the characteristic signal, which frequency is 10 Hz, and more effectively eliminate the harmonic wave, non-integer multiplier frequency component as well as a variety of random interference, so as to more accurately extract the amplitude and phase of the unbalance signal than using hard and soft threshold de-noising method in Fig. 7(c) and Fig. 7(d).

Fig. 7Frequency domain diagram of the original signal and the de-noising signal using adaptive redundant lifting wavelet

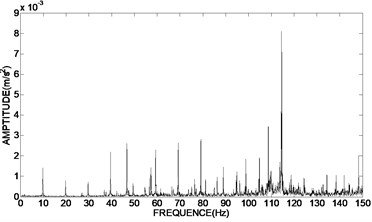
a) The original vibration signal

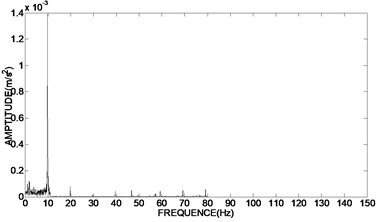
b) Using bivariate threshold function

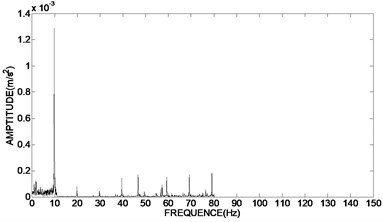
c) Using hard threshold function

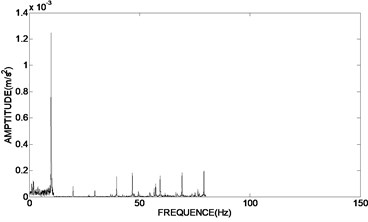
d) Using soft threshold functions

For comparing test result more specifically, the SNR and mean square error (MSE) were introduced to evaluate the de-noising effect [22]:

where $x$ is the sample value of the signal without noise, $\widehat{x}$ is the value of de-noising signal; $N$ is the length of the signal. The SNR is greater and MSE is smaller, the de-noising effect is better. The evaluation results were shown in Table 1.

Compared the results in the Table 1, the vibration signal using the dual variables improved threshold function has the highest SNR (10.4882) and the minimum MSE (3.1031e-004). Experimental results demonstrate that adaptive redundant lifting wavelet combined with the dual variables improved threshold function has the best de-noising effect.

4. Conclusion

In the signal de-noising method based on adaptive redundancy lifting wavelet transform, an improved bivariate threshold function was introduced to process the threshold. Compared with the threshold processing of the conventional threshold function, it can obtain higher SNR and smaller SME. At the same time, by adjusting the two variable parameters, the deviation of the wavelet coefficients was eliminated. In the unbalance vibration signal de-noising of motorized spindle, the new method can retain the original signal feature of amplitude and phase, as well as eliminate noise more effectively, when the actual vibration signal of motorized spindle is low SNR and non-stationary. An effective and reliable vibration signal processing model was provided for high speed and high precision active balancing of motorized spindle. The method has important applications in improving the running accuracy of motorized spindle and performance of the CNC machine.