Detecting multiple small-sized damage in beam-type structures by Teager energy of modal curvature shape

3.1. Teager energy

To intensify features of small-sized damage, a new damage feature of Teager energy [31, 32] of modal curvature shape is created. Let $x_n$ be a sequence of sampling points of a cosine/sine signal:

where $n$ is the sampling number, $\varphi$ is the initial phase and $\mathrm{\Omega }$ is the digital frequency specified by $\mathrm{\Omega }=2\pi f/f_s$, with $f$ being the analog frequency and $f_s$ the sampling frequency. The signal values at three successive points are:

According to the trigonometric identities, Eq. (3) gives:

The Teager energy is defined by:

For an arbitrary signal $f\left(z\right)$, the Teager energy defined on its discrete samplings is given by:

where $\psi$ denotes the Teager energy operator.

The Teager energy operator has an important property [32, 33]:

where $C$ is a constant. Eq. (7) is the theoretical foundation for creation of the new damage feature, the Teager energy of modal curvature shape.

3.2. Teager energy of modal curvature shape

The formulation of Teager energy of modal curvature shape is illustrated on a mode shape of an Euler beam for the major central portion exclusive of boundary-effect area, for which the transverse vibration equation can be expressed in the spatial domain as [34]:

where $\gamma =L\sqrt[4]{{\omega }^2\rho S/EI}$ with $S\text{,}$$\rho \text{,}$ and $\omega$ being cross-sectional area, material density, and angular frequency of the beam, respectively. Let $\zeta =x/L$ with $L$ being the beam length, $\varphi$ the phase angle. The modal curvature of $W\left(\zeta \right)$ is:

On the basis of the fact that local damage induces singularity manifested by a singular peak in a modal curvature [24-28], a local singular peak is introduced into the modal curvature to simulate the damage effect. The singular peak is defined by $C{\prod }_{{\zeta }_1,{\zeta }_2}$ with ${\zeta }_1\approx {\zeta }_2$, where $C$ is the magnitude of the peak and ${\prod }_{{\zeta }_1,{\zeta }_2}$ is an extremely narrow interval in which the value is 1 while zero elsewhere, representing the width of the peak. The simulated modal curvature bearing a singular peak caused by damage is specified by:

With Eq. (10), the capability of $W^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{*}}\left(\zeta \right)$ to reflect damage is quantified by the ratio of the magnitude of the singular peak, $C$, to the magnitude of $W^{\text{'}\text{'}}\left(\zeta \right)$:

The Teager energy of $W^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{*}}\left(\zeta \right)$ can be written in light of Eq. (7) as:

with $\psi \left(W^{\mathrm{\text{'}}\mathrm{\text{'}}}\right(\zeta \left)\right)$ calculating the Teager energy of $W\text{'}\mathrm{\text{'}}\left(\zeta \right)$ by Eq. (5):

Similar to Eq. (11), the capability of $\psi \left(W^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{*}}\right(\zeta \left)\right)$ to reflect damage is quantified by the ratio of the magnitude of the singular peak, $C$, to the magnitude of $\psi \left(W^{\mathrm{\text{'}}\mathrm{\text{'}}}\right(\zeta \left)\right)$:

The contrast ratio of capability between $W^{\text{'}\text{'}*}\left(x\right)$ and $\psi \left(W^{\text{'}\text{'}*}\right(x\left)\right)$ to characterize damage can be measured by an index:

where $f\left(\gamma \right)=(\gamma /\mathrm{s}\mathrm{i}\mathrm{n}\gamma {)}^2$ is a function of values varying from 1 to infinite, and $g(\gamma ,\zeta )={\left(W\left(\zeta \right)\right)}^2$ is a function of values varying from 0 to 1. The amplification effect of $f\left(\gamma \right)$ renders the vast majority of the values of $\alpha (\gamma ,\zeta )$ are greater than 1, as illustrated in Fig. 1 for the sixth mode shape of a C-C beam, and the seventh mode shape of a C-F beam. Similar characteristic can be found for other types of beams with different boundary conditions, indicating that the Teager energy of modal curvature shape can characterize small-sized damage in beams in a more effective fashion than the conventional modal curvature.

Fig. 1α for the sixth mode shape of a C-C beam a) and the seventh mode shape of a C-F beam, b) for ζ over interval (0.15, 0.85)

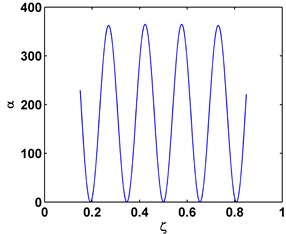
a)

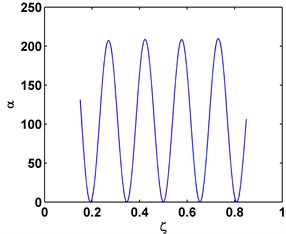
b)

4.1. Analytical model

A crack is modeled as a linear rotational spring [35] with the bending constant determined by the fracture mechanics principle [36]:

where $E$ and $I$ are Young’s modulus and moment of inertia, respectively; $K$ is the bending constant of the spring; $h$ is the beam depth; and $\xi =a/h$ is the crack depth ratio with $a$ being the crack depth. $J\left(\xi \right)$ is the dimensionless local compliance function:

A beam with $n$ cracks can be divided into $n+$1 segments, with an arbitrarily adjacent pair of segments linked by a crack. Fig. 2 illustrates an analytical model of clamped-clamped (C-C) beam with three cracks.

Fig. 2Analytical model of a C-C beam with three cracks

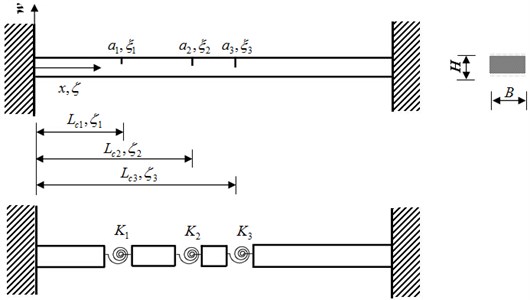
The motion of transverse vibration of a beam segment is described by the governing equation:

where $W_i\left(x\right)$ is the transverse deflection shape of the $i$th beam segment, $W_i^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}\left(x\right)$ is the fourth order derivative of $W\left(x\right)$, and $\lambda =\sqrt[4]{{\omega }^2\rho S/EI}$ with $S\text{,}$$\rho \text{,}$ and $\omega$ being cross-sectional area, material density, and angular frequency of the beam, respectively. Without loss of generality, $\zeta =x/L$, with $L$ being the beam length, is introduced to produce the dimensionless version of Eq. (18) as:

where $\gamma =\lambda L$. The general solution of Eq. (19) is expressed as [34]:

In the case of a C-C beam, the four boundary conditions are given as:

and the four compatible conditions at the location of each crack are specified by:

where ${\zeta }_i$ is the crack location ratio for the $i$th crack.

Substituting Eq. (20) into Eqs. (21) and (22), a group of simultaneous equations with respect to the angular frequency $\omega$ can be obtained as:

where $\mathbf{C}$ is a column vector of $A_i$, $B_i\text{,}$$C_i$, and $D_i\text{,}$$i=\text{1,}\text{2,}\text{…,}n+1\text{,}$ and $\mathbf{D}$ is an $\text{(}n+\text{1)×(}n+\text{1)}$ matrix. To find the nontrivial solution, the frequency determinant of $\mathbf{D}$ is set to zero, leading to the following frequency equation [37, 38]:

Solving Eq. (24) produces a sequence of natural frequencies ${\omega }_j$, $j=\text{1,}\text{2,}\text{…}\text{,}N$. Provided with ${\omega }_j$, we can derive the corresponding coefficient vector ${\mathbf{C}}_j$ from Eq. (23). Substituting ${\omega }_j$ and ${\mathbf{C}}_j$ into Eq. (20) yields the $j$th mode shape. In other types of boundary condition, Eq. (21) can be replaced using the combination of $W=0$ and $W^{\mathrm{\text{'}}\mathrm{\text{'}}}=0$ for a simply supported end; $W=0$ and $W^{\mathrm{\text{'}}}=0$ for a clamped end; and $W^{\mathrm{\text{'}}\mathrm{\text{'}}}=0$ and $W^{\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}}=0$ for a free end.

4.2. Damage identification

Use of the Teager energy of modal curvature shape to detect multiple small-sized damage is verified by identifying three slight cracks using mode shapes analytically obtained following the procedure described in Section 4.1. The beam dimensions are length 500 mm, width 50 mm, and thickness 10 mm. The elastic modulus, Poisson's ratio, and material density are taken as 200 GPa, 0.37, and 800 kg/m³, respectively. Three cracks are located at 100 mm (${\zeta }_1=\text{0.2}$), 200 mm (${\zeta }_2=\text{0.4}$), and 300 mm (${\zeta }_3=\text{0.6}$), each with depth 2 mm. The third, fourth, and fifth modes (Fig. 3) of three cracked beams with the pinned-pinned (P-P), C-C, and clamped-fixed (C-F) boundary conditions, respectively, are used to examine the capability of the Teager energy of modal curvature shape to characterize damage.

Fig. 3Mode shapes of the third, fourth, and fifth mode shapes for the P-P, C-C, C-F beams, respectively

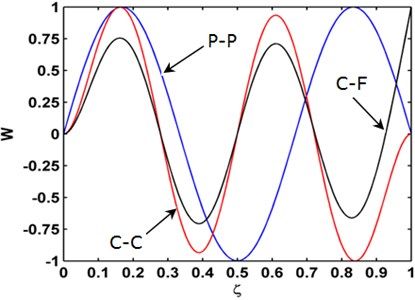
Modal curvatures of these three mode shapes, obtained by second-order central difference method, are shown in Fig. 4. It can be seen that three small singular peaks appear in each modal curvature around the actual crack locations. However, most singular cracks are slim, not enough to provide a solid manifestation of the damage [29, 30].

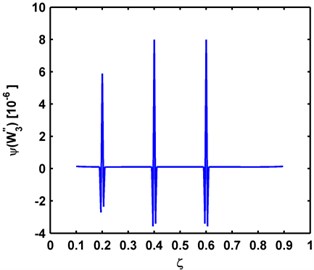
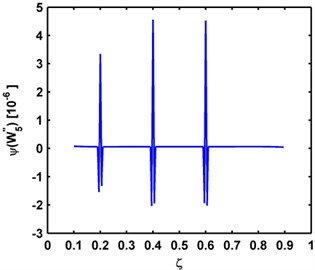
The Teager energy of modal curvature shape for each beam, calculated by Eq. (6), is displayed in Fig. 5, where three singular peaks are predominant, clearly pinpointing the cracks. Compared with the modal curvatures in Fig. 4, the superior capability of the Teager energy of modal curvature shape to characterize multiple small-sized damage is fully demonstrated.

Fig. 4Mode curvatures of the a) third, b) fourth, and c) fifth mode shapes for the P-P, C-C, C-F beams, respectively

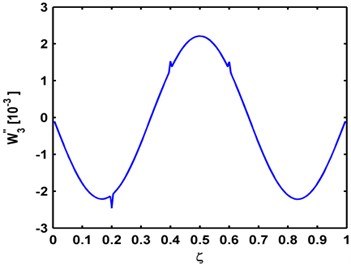
a) Third mode

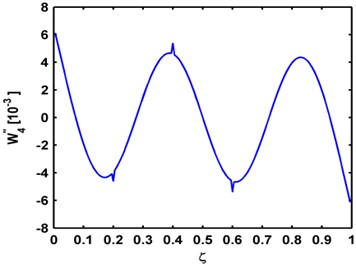
b) Fourth mode

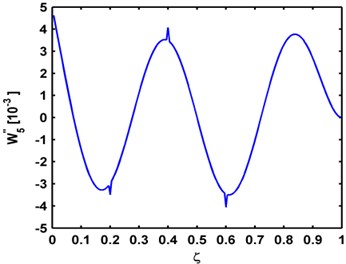
c) Fifth mode

5.1. Set-up

A CFRP beam of length 500 mm, width 10 mm, and thickness 1.5 mm is considered. It consists of five layers in thickness with each layer being around 0.3 mm. The beam is clamped at its bottom end, with the fixing area being through-width and spanning 10 mm from the bottom edge. An electromechanical shaker (B&K® 4809) at 15 mm distant from the fixed end, attached on the damaged side, is used as actuator to excite the beam; meanwhile, a SLV is utilized as a sensor to acquire the out-of-plane velocity response of the beam: the SLV (Polytec PSV-400) scans over 499 measurement points uniformly distributed on the laser inspection region from 10 mm through 496 mm of the intact side of the beam. This region is covered by the retro-reflective tape to facilitate measurement. The dimensionless locations of the three cracks in the laser inspection region are ${\zeta }_1=\text{0.212}$, ${\zeta }_2=\text{0.434}$, and ${\zeta }_3=\text{0.730}$. Three cracks are created by cutting into the beam with a very thin knife to produce three cuts of about width 0.5 mm, depth 0.3 mm in the first layer for the first two cracks, depth 0.5 mm between the first and the second layers for the third crack. Fig. 6 shows the experimental setup.

Fig. 5Teager energy of modal curvature shapes of the a) third, b) fourth, and c) fifth mode shapes for the P-P, C-C, C-F beams, respectively

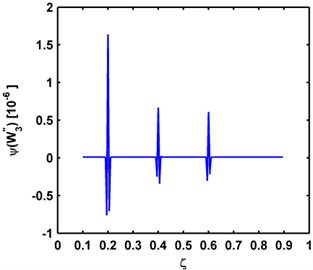
a)

b)

c)

Fig. 6Experimental setup: a) local beam segment containing a crack as marked by ellipse; and b) SLV

a)

b)

5.2. Results

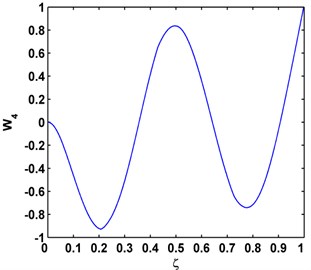
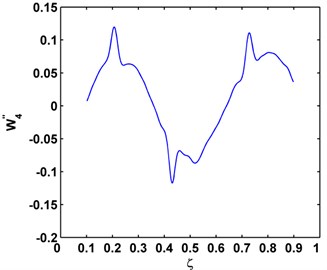
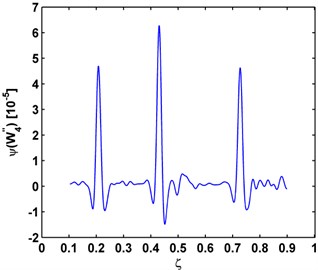
The beam is excited by the shaker at the fourth natural frequency around 3000 Hz and the mode shapes (Fig. 7(a)) are obtained by measuring the vibration responses using the SLV. The modal curvature after denoising is shown in Fig. 7(b), and the Teager energy of modal curvature shape is presented in Fig. 7(c). Fig. 7(b) shows that the damage-induced singular peaks in modal curvatures are largely overwhelmed by the global fluctuation trend of the modal curvature. Dramatically, the singular peaks in the Teager energy of modal curvature shape (Fig. 7(c)) are much more predominant, clearly identifying and locating cracks. Comparing Fig. 7(c) and Fig. 7(b), it can be clearly concluded that the Teager energy of modal curvature shape has greater capabilities to characterize small-sized damage in beams than the conventional modal curvature.

Fig. 7a) Mode shape, b) modal curvature, c) Teager energy of modal curvature shape for damage identification

a)

b)

c)