A new shaft multi-objective optimization dynamic balancing method based on differential search algorithm

Wen, Guangrui; Dong, Xiaoni; Zhang, Henghui

Vibroengineering Procedia

Browse Procedia

Published: 03 November 2014

Check for updates

A new shaft multi-objective optimization dynamic balancing method based on differential search algorithm

Guangrui Wen¹

Xiaoni Dong²

Henghui Zhang³

¹State Key Lab for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University, Xi’an, China

^{2, 3}School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an, China

Corresponding Author:

Guangrui Wen

Cite the article Download PDF

Downloads 1421

Abstract

Combined with the influence coefficient methods and the Holo-balancing theory of shaft system, a new shaft multi-objective optimization dynamic balancing method including energy, uniformity and maximum of the residual vibration is proposed by building a multi-objective fuzzy evaluation function and application of Differential Search (DS) algorithm. The advantage of DS algorithm is studied by comparing with four other optimization algorithms. And the principle of balancing weight optimization of DS algorithm is studied to realize the shaft dynamic balancing. Finally, the validity and effectiveness of the proposed method is verified through a field power generator set balancing case.

1. Introduction

One of the biggest problems which large rotating machinery faced is vibration problem. A large amount of statistical data indicates that the mass unbalance of the rotors is usually the major cause of excessive vibrations of large rotating machinery [1]. Rotary mechanical shaft unbalance would cause flexure and internal stress of rotors, accelerate abrasion of bearing and shaft seal parts, reduce the working efficiency of the machine, which could cause serious accidents [2]. Therefore, the dynamic balancing technology is particularly important for large rotating machinery.

Influence coefficient [3] and modal balance method [4] are widely used methods for balancing in industry field. Holospectrum [5-7] based balancing technique is a relatively new method for balancing [8]. Because of the difference between shaft balancing and single rotor balancing, the influence of measuring surface selection and supporting condition of bearing, it is very difficult to get the optimal result by solving the balancing weight directly.

In nature, many species of living beings benefit from the ability of collective problem-solving of the groups they form through socialization to solve hard problems [9]. Swarm intelligence optimization algorithm is on the basis of this to search solution for a problem by natural or artificial agents through use of collective methods [10]. As a swarm intelligence optimization algorithm, DS algorithm is very flexible and steady [11].

Multipurpose optimizing of shaft balancing is studied, and DS algorithm is employed to solve the problem here.

2. Differential search algorithm

DS is an algorithm developed for solution of optimization problems. DS algorithm simulates the Brownian-like random-walk movement used by an organism to migrate [11].

2.1. The principle of differential search algorithm

It is assumed, in DS algorithm, that a population made up of random solutions of the respective problem corresponds to an artificial-superorganism migrating. In DS algorithm, artificial-superorganism migrates to global minimum value of the problem. During this migration, the artificial-superorganism tests whether some randomly selected positions are suitable temporarily during the migration. If such a position tested is suitable to stopover for a temporary time during the migration, the members of the artificial-superorganism that made such discovery immediately settle at the discovered position and continue their migration from this position on.

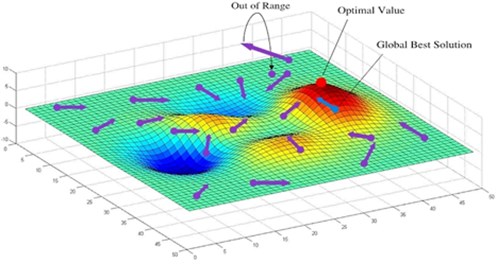
The schematic diagram of DS algorithm is shown in Fig. 1. Fig. 1 depicts the process of the DS algorithm to find the optimal value.

Fig. 1The schematic diagram of DS algorithm

2.2. DS algorithm compared with other algorithms

DE, PSO-w, PSO-cf and SFS algorithm were selected to compare with Differential Search algorithm. In the tests, population is selected for 100. 30 times independent tests were made to each algorithm with suitable parameter settings.

Function 1 is a low-dimensional multimodal function with a few local minimum values:

1

f_{1} = 4 x_{1}^{2} - 2.1 x_{1}^{4} + \frac{1}{3} x_{1}^{6} + x_{1} x_{2} - 4 x_{2}^{2} + 4 x_{2}^{4} .

The global minimum is $f_{1}$ (–0.09, 0.71) $=$ –1.0316. The results are shown in Table 1.

Table 1Experimental results of function 1

Function	Permissible error	Algorithm	The best value	The mean value	The mean iterations	Times of success
$f_{1}$ $G =$ 100	1e-4	DE	–1.0316	–1.0316	24.7	30
		PSO-w	–1.0316	–1.0316	20.7	30
		PSO-cf	–1.0316	–1.0316	20.6	30
		SFS	–1.0316	–1.0316	17.7	30
		DS	–1.0316	–1.0316	36.3	30

Table 2Experimental results of function 2

Function	Permissible error	Algorithm	The best value	The mean value	The mean iterations	Times of success
$f_{4}$ $G =$ 5000	1e-3	DE	9.95e-00	8.10e+01	5000	0
		PSO-w	7.96e-00	2.10e+01	5000	0
		PSO-cf	2.69e+01	6.17e+01	5000	0
		SFS	2.98e-00	6.24e-00	5000	0
		DS	0	0	2061.1	30

Function 2 is a high-dimensional multimodal function with a lot of local minimum values:

2

f_{2} = \sum_{i = 1}^{30} (x_{i}^{2} - 10 \cos (2 π x_{i}) + 10) .

The global minimum is $f_{2} (\vec{0}) = 0$ . The results are shown in Table 2.

It is concluded that DS algorithm is flexible and steady. DS algorithm is more effective to solve problems of high-dimensional multimodal function.

3. Multi-objective optimization of dynamic balance

The weight and angle of the clump weight on each balancing plane are determined through optimization of dynamic balance. The optimization results make vibrations achieve the ideal effect.

3.1. Selection of balance optimization target

Three optimization targets are selected to measure and evaluate the effects of balancing as follows:

3

\min F_{1} (X) = \min \sum x_{i}^{2},

4

\min F_{2} (X) = \min (\max x_{i}),

5

\min F_{3} (X) = \min (\max x_{i} - \min x_{i}),

where, $x_{i}$ is the residual vibration of each measuring point.

Eq. (3) represents the minimum square sum of residual vibrations. Eq. (4) represents the maximum of residual vibration. Eq. (5) represents diversity of residual vibrations between each measuring section.

The multi-objective optimization problem turns to a single object optimization problem by the linear weighted summation method. Because of the differences of magnitude and dimension among each object function, it is liable to happen that some objective functions are always in dominant positions and other objective functions will not be optimized effectively [12]. Therefore, each objective function should be normalized based on fuzzy mathematics theory:

6

μ (F_{t} (X)) = \{\begin{array}{l} 1, & F_{t} (X) = m_{t}, \\ \frac{M_{t} - F_{t} (x)}{M_{t} - m_{t}}, & m_{t} < F_{t} (X) < M_{t}, \\ 0, & F_{t} (X) = M_{t}, \end{array}

where, $M_{t}$ and $m_{t}$ are the maximum and minimum value of the function item $F_{t} (X)$ respectively.

The overall balancing optimization object function is defined as linear weighted summation of all membership functions:

7

H (X) = w_{1} μ (F_{1} (X)) + w_{2} μ (F_{2} (X)) + w_{3} μ (F_{3} (X)),

where, $w_{t}$ , $t = 1, 2, 3$ ; is the weight coefficient of each membership function, and it is determined by the importance of each objective function. Here, considering the leading role of objective function $F_{1} (X)$ , the weight coefficients are set as $w_{1} =$ 0.7, $w_{2} =$ 0.2, $w_{3} =$ 0.1.

3.2. Balancing weight optimization with DS algorithm

Suppose the number of balancing plane is $K$ , the process of balance optimization using DS algorithm can be described below:

1) Design artificial-organism as $X = [m_{1}, α_{1}, m_{2}, α_{2}, \dots, m_{K}, α_{K}]$ , where $m_{i}$ and $α_{i}$ are the weight and angle of the clump weight on the $i$ th balancing plane.

2) Initialize the population, and determine $M_{t}$ and $m_{t}$ of each sub-object function.

3) Calculate the fitness values of initial positions.

4) Calculate the fitness values of stopover sites.

5) Compare the fitness values of stopover sites of artificial-organisms with current positions. If fitness values of stopover sites are better than current positions, update those positions.

6) Go to step 4 to do the iteration, until the optimal solution is found.

4. Application of DS algorithm in power generator set field balancing

The following is a field balancing application of a generator in power plant. The block diagram of the generator is shown in Fig. 2. Balancing planes were remarked with A, B and C in Fig. 2. Vibration measuring sections were selected at bearings of 1#, 2#, 3# and 4#.

Fig. 2Block diagram of the generate set

The transfer matrix of balancing plane was calculated by the previous balancing experiments. Use DS algorithm to optimize the balancing weight. The optimized balancing weights on balancing planes A, B and C are 1152.05 g∠83.65°, 898.00 g∠151.71° and 1151.32 g∠299.43° respectively.

The vibrations before the balancing, after the balancing and after multi-objective optimization are given in Table 3.

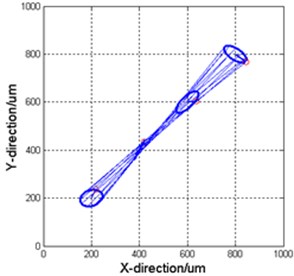
The 3D holospectrum of the vibrations are shown in Figs 3, 4 and 5 respectively.

Table 3Vibrations of power generator set

Vibration measuring section		Vibration before balancing	Vibration after balancing	Vibration after multi-objective optimization
1#	$X$ (um∠°)	116.5∠136	64.2∠68.0	44.7∠174.2
1#	$Y$ (um∠°)	64.0∠28	57.4∠304	41.1∠86.9
2#	$X$ (um∠°)	54.0∠114	19.2∠139	29.7∠69.6
2#	$Y$ (um∠°)	79.0∠65	36.3∠34	42.6∠46.2
3#	$X$ (um∠°)	117.0∠110	49.6∠82	45.5∠46.3
3#	$Y$ (um∠°)	110.0∠18	78.8∠351	45.5∠4.7
4#	$X$ (um∠°)	49.0∠276	54.9∠104	45.5∠68.3
4#	$Y$ (um∠°)	18.5∠176	37.2∠25	29.8∠292.4

Fig. 3Original vibrations

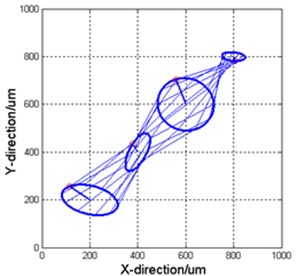
Fig. 4Vibrations after balancing

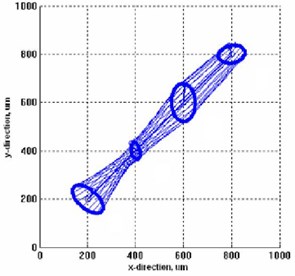
Fig. 5Vibrations used by DSA

5. Conclusions

In this paper, the maximum, uniformity and square summation of residual vibration are selected to be the optimization sub-objects for shaft system balancing, which meets the requirements of field dynamic balancing. Optimization and coordination among sub-objects are realized through multi-objective optimization function based on fuzzy mathematics theory. The principle of optimization of balancing weight with DS algorithm is studied. Compared with other four algorithms (DE, PSO-w, PSO-cf, SFS), DS algorithm is very flexible and steady. The effectiveness and advantage of the proposed method is verified by a practical field balancing application of generator set.

References

Kou SH. L. Flexible rotor morbid equation using balance equation of influence coefficient method. Thermal Power Generation, Vol. 12, 2005, p. 13-16.

Search CrossRef
Wu S. T. The principle and technology of dynamic balance of large units. Xi’an, XJTU, 2003.

Search CrossRef
Grobel L. P. Balancing turbine generator rotors. General Electric Review, Vol. 56, Issue 4, 1953, p. 22.

Search CrossRef
Goodman T. P. A least-squares method for computing balance corrections. ASME Transactions, Journal of Engineering for Industry, Vol. 86, Issue 3, 1964, p. 273-279.

Search CrossRef
Qu L. SH., Liu X., Chen Y. D. Discovering the holospectrum. Noise and Vibration Control Worldwide, Vol. 20, Issue 2, 1989, p. 58-62.

Search CrossRef
Qu L. SH., Liu X., Peyronne G., Chen Y. D. The holospectrum: a new method for rotor surveillance and diagnosis. Mechanical Systems and Signal Processing, Vol. 3, Issue 3, 1989, p. 255-267.

Search CrossRef
Qu L. SH., Chen Y. D., Liu J. Y. The holospectrum: a new FFT based rotor diagnostic method. Proceedings of the 1st International Machinery Monitoring and Diagnostics Conference, Las Vegas, Nevada, 1989, p. 196-201.

Search CrossRef
Qu L. SH., Qiu H., Xu G. H. Rotor balancing based on holospectrum analysis: principle and practice. China Mechanical Engineering, Vol. 9, Issue 1, 1998, p. 60-63.

Search CrossRef
Kennedy J., Eberhart R. C., Shi Y. H. Swarm Intelligence. San Francisco, Morgan Kaufmann Publishers, 2001.

Search CrossRef
Feng CH. SH. Swarm intelligence optimization algorithm and its application. Hefei, 2009.

Search CrossRef
Pinar C. Transforming geocentric Cartesian coordinates to geodetic coordinates by using Differential Search algorithm. Computers and Geosciences, Vol. 46, 2012, p. 229-247.

Search CrossRef
Jia ZH. H., Chen H. P., Sun Y. H. Multi-objective particle swarm optimization algorithm for flexible job shop scheduling. Journal of Chinese Computer Systems, Vol. 29, Issue 5, 2008, p. 885-889.

Search CrossRef

About this article

Received

Accepted

28 September 2014

Published

03 November 2014

Keywords

differential search algorithm

dynamic balancing

multi-objective optimization

shaft system

Acknowledgements

The research was financially supported by the project (51365051) of Natural Science Foundation of China.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.