Global analysis of the nonlinear Duffing-van der Pol type equation by a bifurcation theory and complete bifurcation groups method

1. Introduction

The work is devoted to the research of the regular and chaotic determined oscillations in the non-linear dynamical system describing processes and phenomena in several real problems [1]. Among these, the damped, driven Duffing oscillator and the van der Pol oscillator have played a paradigmatic role in the development of the field of applied nonlinear dynamics [2-4]. The work presents the analysis of an origin of periodic, almost periodic (quasi-periodic) and chaotic oscillations in the nonlinear driven Duffing-van der Pol type systems with application of the systematic approach on the basis of a method of complete bifurcation groups [5-6].

2. Dynamical model and research methods

In this paper, periodic and non-periodic steady or transition oscillations are observed in computer-simulated solutions of the second-order nonlinear ordinary differential Eq. (1):

where ${F\left(x\right)=a}_{1}x+a_2{x}^2+a_3{x}^3$ is a restoring force with nonlinear symmetric or non-symmetric Duffing type characteristic, $F\left(x,\dot{x}\right)=b_1\left(b_2{x}^2-1\right)\dot{x}$ is a nonlinear damping van der Pol type force, $F\left(\dot{x}\right)=b\dot{x}$ is a linear damping force and $F\left(t\right)=h\cos \left(wt\right)$ is an external periodical force with period $T=2\pi /w$, frequency $w$, amplitude $h$.

The main task of work is the research of the influence of the amplitude and frequency of external harmonic forcing on forced regular and chaotic oscillations of nonlinear driven Duffing-van der Pol type systems as well as to study rare nonlinear effects. This investigation will use the method of complete bifurcation groups. Basic propositions of the theory for research and the global bifurcation analysis of the nonlinear dynamical system on the basis of a method of complete bifurcation groups are published in the papers [5-6]. At the systematic approach the following activities for the certain parameters of researched system after display of complete bifurcation groups are carried out: the additional analysis of various periodic attractors, forecasting of quasi-periodic oscillations and chaotic attractors, projection of areas of attraction on Poincaré’s plane in case of multiplicity phenomena, and the study of a birth of regular and chaotic attractors. Research results have been obtained by direct numerical simulation using software SPRING [7].

The method of complete bifurcation groups and the complex of algorithms and programs allow us to systematically find complete bifurcation groups for non-linear dynamical models and to study interaction of various bifurcation groups. The method of complete bifurcation groups assumes the following:

a) The research of periodic skeletons: search of all bifurcation groups (nT – designation of the bifurcation group the basis of which is the regime of nth order) with periodic regimes corresponding to them (Pn - designation of a regime of nth order). For search of regimes of the various orders it is recommended to use values of parameters from area with the infinite number of unstable periodic regimes (UPI).

b) An estimation of stability of all found periodic regimes with calculation of multiplicators at the selected values of space of parameters. Continuation on a parameter (on a solution branch) of stable and unstable periodic regimes of each bifurcation group: the main 1Т and subharmonic nT; display of complete bifurcation groups in bifurcation charts.

It is offered to apply the systematic approach to the research of rare attractors (RA), as well as steady oscillations accompanying them. In this case the birth of a rare attractor at a change of bifurcation parameter, and steady oscillations (regular or chaotic attractors) exist in a small range of a changing parameter [5-8].

For display of the irregular stationary regimes (chaotic and quasi-periodic attractors) in bifurcation charts the scanning method is used to determine phase space of the quantitative value of appropriate coordinates of results of integration after termination of the transition process at driving on parameter from one initial condition belonging to the area of an attraction of a stationary regime.

In typical dynamical systems the birth of chaotic oscillations is connected to the main bifurcation group 1Т, subharmonic bifurcation groups nT and their coexistence. Chaotic oscillations are possible only in the area with the infinite number of unstable periodic infinitums UPI. Transition process depends on all bifurcation groups located in the field of considered initial conditions. Thus, in the presence of infinite number of unstable periodic infinitums UPI in the system, chaotic transition processes or chaotic attractors (ChA-n) of certain bifurcation groups are observed [8].

3. Complete bifurcation analysis for regular and chaotic dynamics research

The given research dwells upon formation of typical bifurcation groups and a birth of regular and chaotic oscillations in the nonlinear Duffing-van der Pol type systems with exterior periodic influence. The coexistence of 1T regime and quasi- periodic oscillations is investigated. The transfer to globally steady-state regime 1T and disappearance of quasi- periodic oscillations under the change of the external periodic forcing frequency are shown. In such systems under external periodic excitation new bifurcation groups have been discovered, which are connected with the birth of quasi- periodic and chaotic oscillations.

Fig. 1 displays the analysis of periodic, quasi-periodic and chaotic oscillations (displacement $x$) of bifurcation groups 1Т, 2T, 3T, 5T, 7T, 10T, 17T, 23T and 36Т on the basis of the systematic approach. Layout of various bifurcation groups in the same range of parameter (under the change of the frequency $w$ of external harmonic forcing) is typical for nonlinear Duffing-van der Pol type systems. Fig. 2 illustrates the bifurcation diagrams with dependence of stationary regime’s amplitude $A_x$ on excitation force frequency.

Stationary non-periodic oscillations are global or coexistent with other periodic attractors. For example, at $w=$6.63, Fig. 3 illustrates the coexistence of a non-periodic attractor and periodic regime P3 ($x=$–5...5, $v=$ –10...10, 150×300 cells). Domains of attraction of periodic regime P3 and non-periodic attractors are constructed on Poincaré plane.

Fig. 1Bifurcation diagrams (dependence of stationary regime’s displacement x on excitation force frequency w): a) the scanning method bifurcation diagram; b) continuation on a parameter w (on a solution branch) of stable and unstable periodic regimes of each twins bifurcation group: the main 1Т and subharmonic nT: 2T, 3T, 5T, 7T, 10T, 17T, 23T, 36T; c) complete bifurcation diagram of stable, unstable periodic solutions, quasi-periodic motions and chaotic attractors of 16 bifurcation groups (1T, two 2T, three 3T, 5T, five 7T, 10T, 17T, 23T, 36T) of the driven Duffing-van der Pol oscillator. The equation parameters: a1= 1, a2= 0, a3= 2.5, b= 0, b1= 1, b2= 1, h= 20, w=var

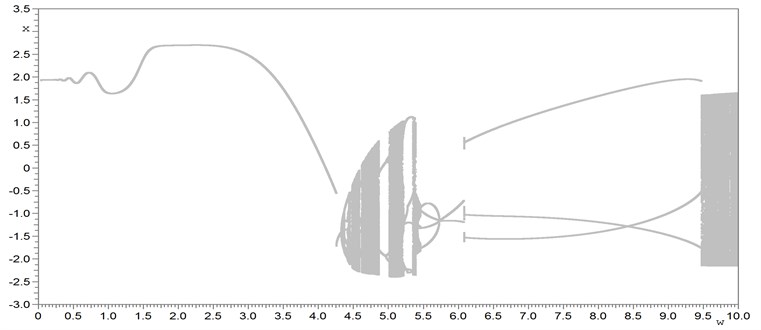
a)

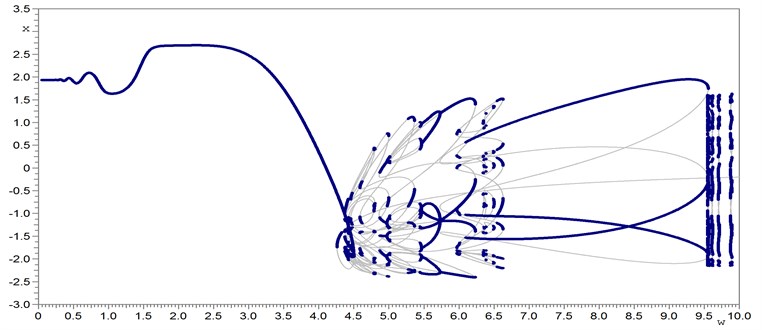
b)

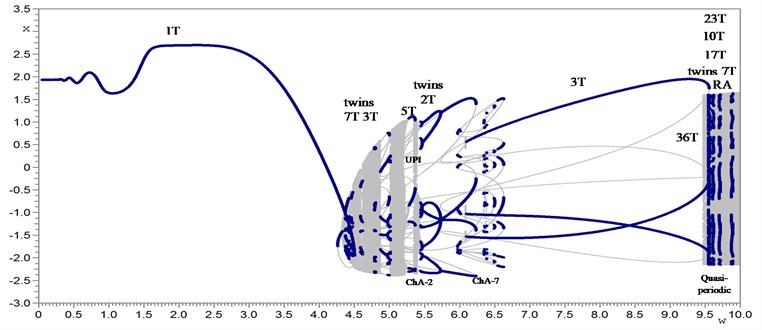
c)

Fig. 2Bifurcation diagrams (dependence of stationary regime’s amplitude Ax on excitation force frequency w): a) Complete bifurcation diagram of stable an unstable periodic solutions continuation on a parameter w (on a solution branch of each bifurcation group: the main 1Т and subharmonic nT: 2T, 3T, 5T, 7T, 10T, 17T, 23T, 36T; b) bifurcation diagrams fragment (3T, two 7T, 10T, 17T, 23T, 36T) of the driven Duffing-van der Pol oscillator under the change of the frequency of external harmonic forcing. The equation parameters: a1= 1, a2= 0, a3= 2.5, b= 0, b1= 1, b2= 1, h= 20, w=var

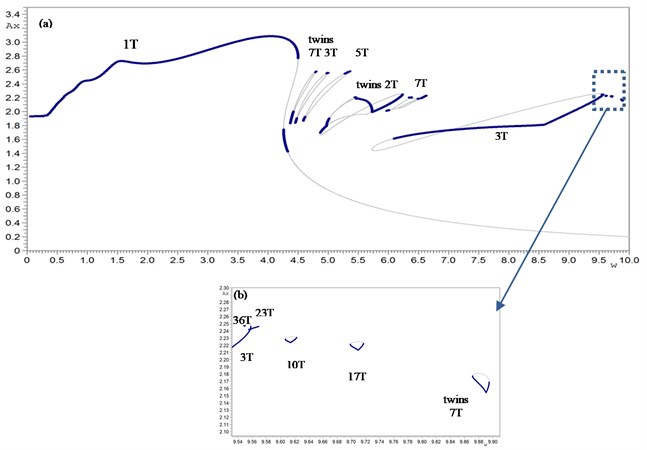
Fig. 3a) P3 attractor on the Poincaré plane (three symbols of the cross) and phase trajectories (gray) initial conditions: x= 0.922745, v= –0.722557, b) non-periodic attractor on the Poincaré plane (symbols of the cross) and phase trajectories (gray); initial conditions: x= –0.406753, v= –4.237863; 300 periods, c) coexisting of two attractors (P3 and non-periodic) on the Poincaré plane, d) domains of attraction for non-periodic attractor (light gray) and P3 (dark gray) regime. The nonlinear driven Duffing-van der Pol equation parameters: a1= 1, a2= 0, a3= 2.5, b= 0, b1= 1, b2= 1, h= 20, w= 6.63

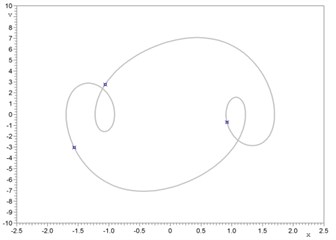
a)

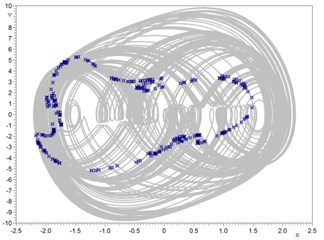
b)

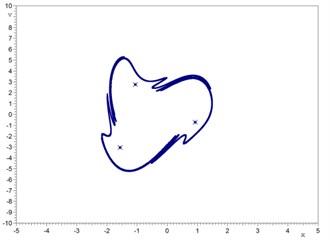
c)

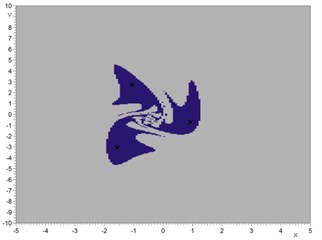
d)

As a result of numerical researches of nonlinear systems at change of parameters has been established that the method of complete bifurcation groups allows to regularly find nonlinear effects and to investigate conditions of their occurrence. The nonlinear effects in many cases can be useful to realization of operating conditions of nonlinear dynamical systems of the different nature.

4. Conclusions

Application of the systematic approach while the study of forced oscillations on the basis of a method of complete bifurcation groups allows us to clarify the origin of the researched regular and chaotic oscillations and to classify the various attractors according to the amount of periodic skeletons and order of bifurcation groups. Results of researches are recommended to be considered for a prediction and prevention of attractors coexisting (multiplicity), chaotic oscillations, quasi-periodic attractors and catastrophic situations in mechanical, electrical and other nonlinear dynamical systems.