Abstract
In order to investigate the longitudinal pounding effect of highway bridges with high-piers under strong ground motions, multiple shaking tables tests of a 1/10 scaled continuous rigid frame and simply-supported girder bridge with high-piers were carried out. The pounding responses of the bridge model under different earthquake excitations including the uniform excitation and the traveling wave excitation were studied, and the effectiveness of the dampers and isolation bearings for reducing the seismic pounding effect were analyzed and discussed. Test results indicate that the traveling wave effect is the important factor in seismic pounding response of high pier bridges. Additional dampers can mitigate the pounding effect apparently and play a role in reducing seismic response for bridge superstructures. Compared with conventional rubber bearing (RB), the decreases in the relative displacement and the pounding force between adjacent girders were 30 % and 55 % with lead rubber bearing (LRB) in this experiment, respectively. Seismic pounding effect of bridge superstructures depends on different structural dynamic properties of adjacent girders and characteristics of ground motions.
1. Introduction
Reinforced concrete (RC) bridges with high-piers are widely used in the high seismic intensity mountainous zone. Substructures of these bridges are common adopted hollow section bridge columns which can offer an optimal strength/mass ratio and stiffness/mass ratio for bridges in seismic regions and reduce the mass contribution of the column to seismic response, and also reduce the tendency for thermally-induced cracking at an early age resulting from heat-of-hydration temperature variations [1]. Superstructures of these bridges are a combination of continuous rigid frame bridge and multi-span simply-supported bridges, and usually are provided with several expansion joints to minimize temperature induced stresses. Recent earthquakes such as Wenchuan earthquake (M8.0, 2008), Yushu earthquake (M7.1, 2010), and Lushan earthquake (M7.0, 2013) in China, have repeatedly demonstrated the vulnerabilities of existing RC bridges, especially RC bridges with hollow section high-piers were seriously damaged and even collapsed. Figure 1 shows the fall down of the main girder of Miaoziping Bridge during 2008 Wenchuan earthquake in China [2]. Pounding at expansion joints is one of the major causes of longitudinal unseating of continuous bridge under strong earthquake excitations. Pounding occurs when the movement of the closing girders at expansion joint exceeds the expansion joint gap. Namely, pounding is induced by relative movement of the adjacent girders at the expansion joint. The movement can be caused by different structural dynamic properties between adjacent girders and various characteristics of ground motions, including traveling wave effect, attenuation effect, incoherence effect and site effect [3].
A large number of studies have been investigated pounding effects for bridges under seismic excitations [4-9]. Pounding force models and analytical methods have been developed according to structural pounding phenomena under strong earthquakes [10-15]. However, due to limitations of earthquake testing facilities, previous experimental research primarily focused on bridge components [16-18], while the researchers seldom paid attention to the testing of seismic performances for the entire bridge structure [19-21]. With an objective to investigate the seismic pounding response of the elevated bridge system, this paper discusses multiple shaking tables testing of a combined bridge with continuous rigid frame and simply-supported girder under various earthquake excitations. Multiple shaking table tests of a 1/10 scaled continuous rigid frame and simply-supported girder bridge were conducted. Furthermore, the pounding response of the scaled model under the uniform and traveling wave excitations is investigated. In addition, the effectiveness of dampers and isolation bearings for reducing the seismic pounding responses is analyzed and discussed as well.
Fig. 1Fallen girder of the Miaoziping bridge (2008 Wenchuan earthquake, China)


2. Experimental program
2.1. Bridge model
The prototype high pier bridge (overall length is 160 m) with hollow section consists of a continuous rigid frame bridge (spans length is 35 m + 60 m + 35 m) and a simply supported girder bridge (span length is 30 m). In view of the shaking table capacity, a 1/10 scaled prototype high pier bridge was conducted based on the prototype bridge.
The detailed descriptions of the bridge model are shown in Figure 2. To satisfy the mass demand of superstructures with concrete box girder, the additional mass is uniformly distributed on the decks. All piers of the RC bridge have length of 3.0 m. The transverse and longitudinal width of the hollow section is 0.4 m and 0.3 m, respectively; the wall thickness is 0.1 m.
Fig. 2The 1/10 scaled bridge model

One of the principle methods for pounding mitigation is to adopt supplemental damping under strong earthquake. Three orifice-type viscous dampers were installed between a deck and a pier, and the maximum output force is 30 kN. Parameters of the viscous dampers are shown in Table 1. In addition, a tension-compression sensor was added to each piston to monitor the output force.
The initial separation distance between adjacent girders was approximately 6 mm, as suggested by Chinese code for design of highway bridges. A steel tube with diameter of 50 mm was equipped in the center of the section for the continuous rigid frame bridge, and a steel hemisphere with diameter of 10 mm facing towards the steel pipe was installed in the identical position for the simply-supported bridge. More details for the two components are shown in Figure 3.
Fig. 3Model bridges and the upper structure and interface form of bridge pier

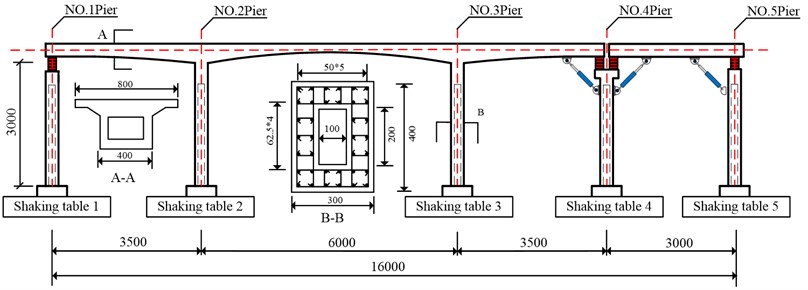
Table 1Parameters of the viscous dampers
Inner diameter / m | Diameter of piston head / m | Length of piston head / m | Diameter of piston rod / m | Diameter of damping hole / m | Length of damping hole / m | Number of damping hole | Viscosity of viscous liquid / cst |
0.05 | 0.05 | 0.05 | 0.028 | 0.002 | 0.05 | 4 | 100 |
Fig. 4Selected accelerograms for the tests
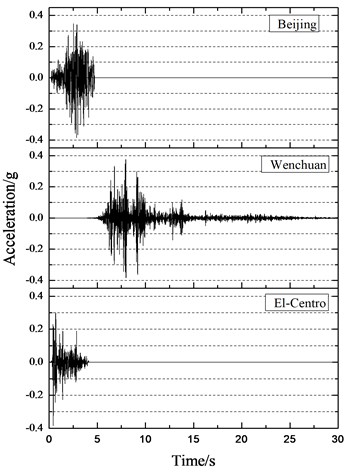
Fig. 5Fourier spectrum
2.2. Selection of earthquake motion input
The tests were conducted on five sub-shaking tables at the Key Laboratory of Urban Security and Disaster Engineering of Beijing University of Technology. As shown in Figure 4, three actual acceleration records are selected for tests: El-Centro wave, Wenchuan wave and Beijing wave. The peak acceleration of the ground motion is 1.1 g (g is gravity acceleration). The specified input acceleration values are shown in Table 2. The excitations are imposed in longitudinal direction of the bridge.
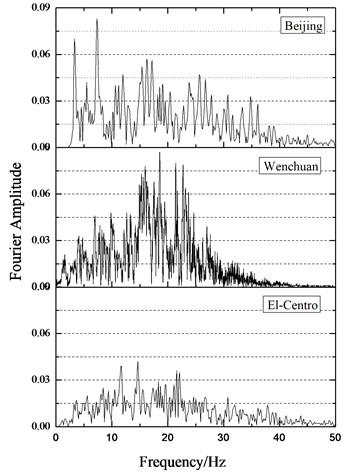
The Fourier spectrum of the three ground motions are shown in Figure 5. Considering the scaling factor of the bridge model, the accelerograms are compressed by a factor of 3.6 to meet the similitude requirements. Simultaneously, peak ground acceleration is modified to 1.1 g.
To verify the traveling wave effect, time lags of the ground motion between the different locations are considered. Time lags of the piers from No. 2 to No. 5 are in sequence 1 s, 1.5 s, 1 s and 1 s than previous piers.
Table 2Specified values of input excitations
No. | Input excitations | PGA (g) | Excitation mode |
1 | El-Centro | 1.10 | Uniform excitation/Traveling-wave excitation |
2 | Wenchuan | 1.10 | Uniform excitation/Traveling-wave excitation |
3 | Beijing | 1.10 | Uniform excitation/Traveling-wave excitation |
3. Results of shaking table tests
3.1. Pounding effect with isolation bearings
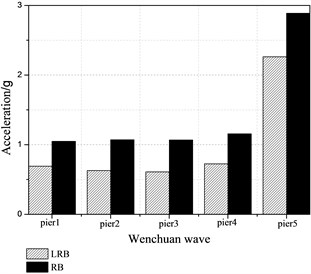
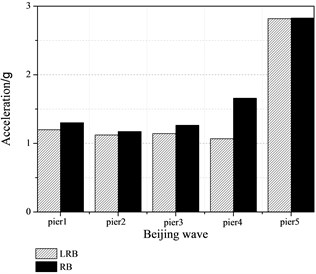
The peak accelerations at the top of piers equipped with lead rubber bearing (LRB) and rubber bearing (RB) are shown in Figure 6. It can be concluded that the peak acceleration responses of bridge model are relatively smaller with LRB compared with RB, and the maximum values reduce by 45 % and 33 % for the excitations of Wenchuan wave and Beijing wave, respectively.
The peak relative displacements between adjacent girders and the strain values of the steel tube are shown in Table 3 and Table 4. The relative displacements of the superstructures and the tube strains are relatively smaller with LRB than RB under uniform excitations. Focusing the attention on the traveling wave excitations, the relative displacement reduces by 24.79 % and the steel tube strain reduced by 61.18 % for Wenchuan wave. Also, the reductions of the relative displacement and the tube strains are 25.00 % and 50.70 % for Beijing wave, respectively.
As compared to RB, equipped with LRB can significantly reduce the seismic pounding effect of the bridge superstructures under both traveling wave excitations and uniform wave excitations.
Fig. 6Peak acceleration at the top of piers with LRB and RB
a)
b)
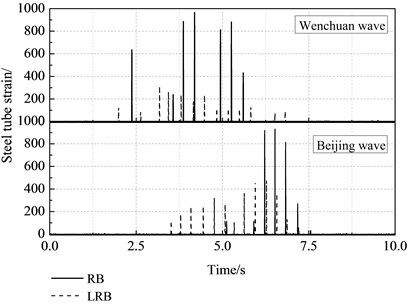
Time history of the relative displacement and the tube strain are shown in Figure 7 and Figure 8. Clearly, the relative displacement and the tube stain have significant reductions, when the bridge equipped with LRB. The pounding times for LRB and RB are 7 and 19 under the Wenchuan earthquake motion, also 6 and 29 under Beijing earthquake motion, respectively. Thus, few fierce pounding times are changed into extensive slight poundings when the LRB is equipped. Meanwhile, the pounding effects are mitigated, and the start of pounding is earlier.
It is obvious that laminated rubber bearing with a cylinder of lead, providing damping energy dissipation which can significantly mitigate the pounding response. Hence the appropriate isolation device has the ability to reduce pounding damage even avoid it.
Table 3Maximum relative displacement between adjacent girders (unit: mm)
Relative displacement | (Wenchuan) | (Beijing) | ||
Uniform excitation | Traveling wave excitation | Uniform excitation | Traveling wave excitation | |
RB | 9.808 | 14.632 | 8.373 | 12.439 |
LRB | 5.263 | 11.004 | 7.320 | 9.329 |
Amplitude increase | 46.34 % | 24.79 % | 12.58 % | 25.00 % |
Table 4Maximum strains of the tube (unit: με)
Steel tube strain | (Wenchuan) | (Beijing) | ||
Uniform excitation | Traveling wave excitation | Uniform excitation | Traveling wave excitation | |
RB | 966.319 | 1185.733 | 931.659 | 1612.615 |
LRB | 312.069 | 460.263 | 474.478 | 795.044 |
Amplitude increase | 67.71 % | 61.18 % | 49.07 % | 50.70 % |
Fig. 7Time history of the relative displacement
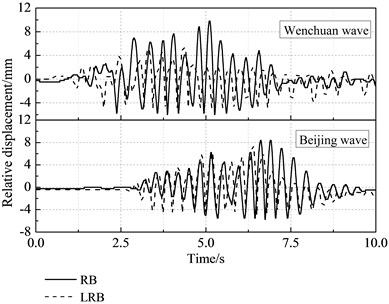
Fig. 8Time history of the tube strain
3.2. Pounding effect with dampers
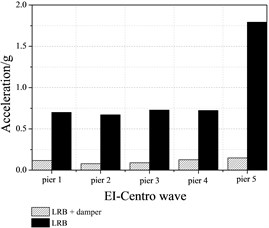
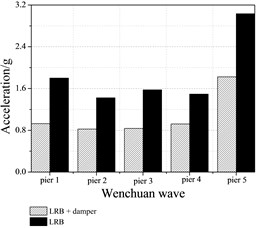
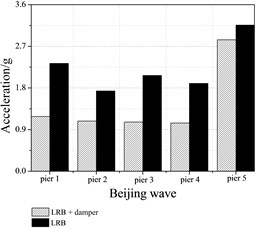
The bar graphs of the peak acceleration at the top of piers with and without dampers are shown in Figure 9. It is found that the peak accelerations are smaller with dampers than without them. When additional dampers are equipped, the reduction rates of the acceleration at pier top are 83.31 %, 35.35 %, 44.92 % for the El-Centro earthquake, Wenchuan earthquake and Beijing earthquake, respectively. The bridge seismic response will reduce with additional damping increases.
The maximum relative displacements between adjacent girders and the tube strains, shown in Table 5 and Table 6, which shows that both parameters have significant reductions, when the bridge equipped with dampers. Conversely, comparing the bridge without damper, it should be noted that the increase of the maximum relative displacement is 4.31 % under uniform excitations for Wenchuan earthquake and the maximum tube strain is increased by as much as 14.39 % under travel wave excitations for Wenchuan earthquake.
The results illustrate that the mitigation for pounding effect of dampers is closely related to the earthquake excitation and spatial variation of ground motions.
Fig. 9Peak acceleration at the top of piers
a)
b)
c)
Fig. 10Time history the tube strain
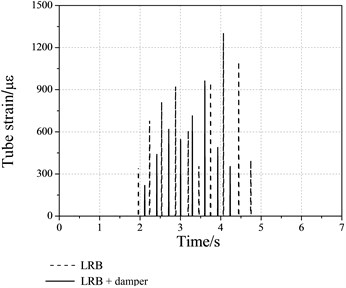
Fig. 11Time history of the relative displacement
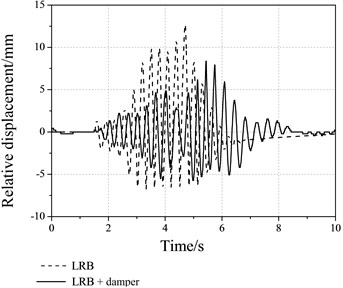
Table 5Maximum relative displacement between adjacent girders (unit: mm)
Relative displacement | (El-Centro) | (Wenchuan) | (Beijing) | |||
Uniform excitation | Traveling wave excitation | Uniform excitation | Traveling wave excitation | Uniform excitation | Traveling wave excitation | |
LRB | 5.263 | 6.459 | 5.263 | 11.004 | 7.320 | 9.329 |
LRB+damper | 3.588 | 4.306 | 5.490 | 10.286 | 5.741 | 9.090 |
Amplitude increase | 31.83 % | 33.33 % | –4.31 % | 6.52 % | 21.58 % | 2.56 % |
Table 6Maximum strains of the tube (unit: με)
Tube strain | (El-Centro) | (Wenchuan) | (Beijing) | |||
Uniform excitation | Traveling wave excitation | Uniform excitation | Traveling wave excitation | Uniform excitation | Traveling wave excitation | |
LRB | 246.839 | 322.526 | 312.069 | 460.263 | 474.478 | 795.044 |
LRB+damper | 4.696 | 5.712 | 286.099 | 526.522 | 295.843 | 715.099 |
Amplitude increase | 97.99 % | 98.23 % | 8.32 % | –14.39 % | 37.65 % | 10.06 % |
The time history of the tube strain shown in Figure 10, reveals that the pounding time for the bridge without dampers is 14 times, which is 1.4 times more than equipped with dampers. It is demonstrated that the pounding times and force are both significantly decreased when the damper is equipped. The relative displacement reduced by 50 % with dampers, while the displacement decay is deferred, as shown in Figure 11.
The damping effect of the damper is concerned with not only the input excitations but also the characteristics of bridge structures. Therefore, selected damper should be considered the sit conditions and the optimize parameters of the damper.
3.3. Influence of traveling wave excitation on pounding effect
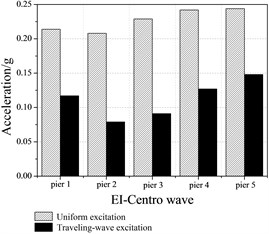
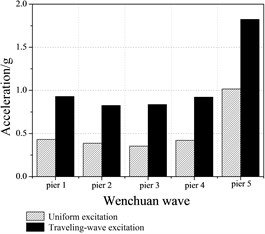
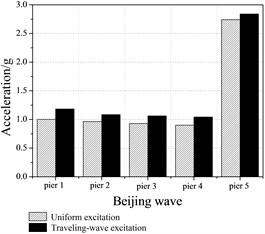
Peak accelerations of the cap beam under various earthquake excitations is shown in Figure 12. From Figure 12 we can see that the peak acceleration at cap beam under traveling wave excitations is greater than uniform excitations for Whenchuan earthquake and Beijing earthquake. Conversely, for the EI-Centro earthquake, the peak acceleration is decreased by 163 % under travelling wave excitations.
The maximum relative displacements between adjacent girders and the tube strains under various earthquake excitations are shown in Table 7 and Table 8. When compared to the uniform excitations, the relative displacements between adjacent girders under traveling wave excitation are larger, while the degree of influence is varied with the characteristic of ground motion.
Fig. 12Peak acceleration of the cap beam under different earthquake excitations
a)
b)
c)
Table 7Maximum relative displacement between adjacent girders (unit: mm)
Relative displacement | (El-Centro) | (Wenchuan) | (Beijing) | ||
LRB | RB | LRB | RB | LRB | |
Uniform excitation | 5.263 | 9.808 | 5.263 | 8.373 | 7.320 |
Traveling wave excitation | 6.459 | 14.632 | 11.004 | 12.439 | 9.329 |
Amplitude increase | 22.72 % | 49.18 % | 109.08 % | 48.56 % | 27.45 % |
Table 8Maximum strains of the tube (unit: με)
Tube strain | (El-Centro) | (Wenchuan) | (Beijing) | ||
LRB | RB | LRB | RB | LRB | |
Uniform excitation | 246.839 | 966.319 | 312.069 | 931.659 | 474.478 |
Traveling wave excitation | 322.526 | 1185.733 | 460.263 | 1612.615 | 795.04 |
Amplitude increase | 30.66 % | 22.71 % | 47.49 % | 73.09 % | 67.56 % |
Fig. 13The time history curve of steel tube strain
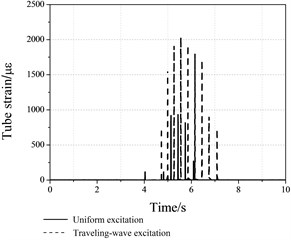
Fig. 14The time history curve of relative displacement
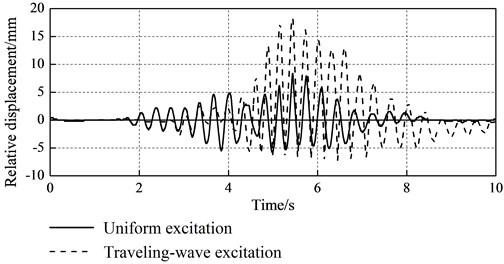
Time history of the tube strain and the relative displacement between adjacent girders under uniform excitations and traveling wave excitations for Beijing earthquake are shown in Figure 13 and Figure 14. Under traveling wave excitation, the duration of the pounding is nearly double as uniform excitations, and the pounding force is also much larger than the uniform excitations. The maximum relative displacement between adjacent girders under traveling-wave excitations is doubled as compared with uniform excitations.
Evidently, the traveling wave excitation has significant influence on seismic pounding responses of bridge superstructures, but the seismic pounding responses under traveling wave excitation are complex and indeterminate.
3.4. Influence of seismic spectra characteristics on pounding effect
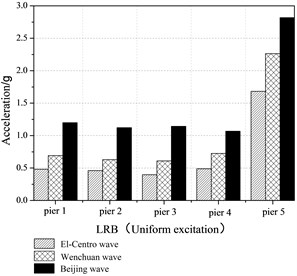
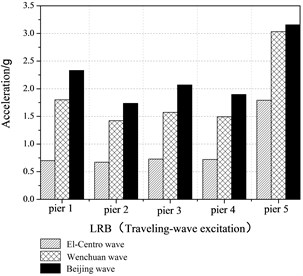
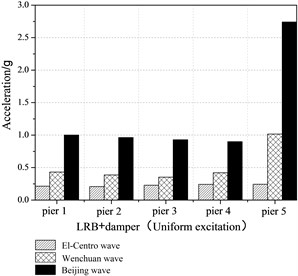
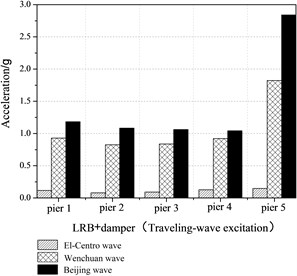
As shown in Figure 15, seismic responses of the bridge model under Beijing earthquake including peak accelerations, relative displacement and tube strains is the largest. The reason is that the natural period of the bridge model is 0.246 s using the results of the white noise excitations. The Fourier spectra of the three earthquakes are shown in Figure 5. It is clearly evident that the natural period of the bridge model is close to the predominant period (0.15 s-0.4 s) of the Beijing earthquake. Namely, the dominant frequency of Beijing earthquake covers the natural frequency of the bridge model.
Fig. 15Peak acceleration at the top of piers
a)
b)
c)
d)
Table 9Maximum relative displacement between adjacent girders (unit: mm)
Relative displacement | Uniform excitation | Travelingwave excitation | ||||
LB | RLB | RLB+Damper | LB | RLB | RLB+Damper | |
(El-Centro) | - | 5.263 | 3.588 | - | 6.459 | 4.306 |
(Wenchuan) | 9.808 | 5.263 | 5.490 | 14.632 | 11.004 | 10.286 |
(Beijing) | 8.373 | 7.320 | 5.741 | 12.439 | 9.329 | 9.090 |
Table 10Maximum strains of the tube (unit: με)
Tube strain | Uniform excitation | Traveling wave excitation | ||||
LB | RLB | RLB+Damper | LB | RLB | RLB+Damper | |
(El-Centro) | - | 246.839 | 4.969 | - | 322.526 | 5.712 |
(Wenchuan) | 966.319 | 312.069 | 286.099 | 1185.733 | 460.263 | 526.522 |
(Beijing) | 931.659 | 474.478 | 295.843 | 1612.615 | 795.044 | 715.099 |
The maximum relative displacements between adjacent girders and the tube strains under various earthquake excitations are shown in Table 9 and Table 10. When the LRB and the dampers are both equipped, the largest maximum tube strain of the pounding effect is for Beijing earthquake, which is equal to 125 times for El-Centro earthquake. Evidently, the pounding effects of the bridge model with isolation bearings and additional dampers are different under various earthquake motions, which are closely related to spectra characteristics of the ground motion. When the dominant frequency of the earthquake motion covers the basic frequency of bridge structures, seismic pounding responses of the bridge structures will increase significantly.
In order to avoid the unfavorable earthquake responses, adopting isolation and dissipation technologies, such as isolation bearing and additional damper, have the ability to reduce the basic frequency of the structural vibration and dissipate the seismic energy input.
4. Conclusions
Multiple shaking table tests of seismic pounding responses of a continuous rigid frame and simply-supported girder bridge model under uniform excitation and traveling-wave excitation were conducted in this paper. In order to mitigate pounding effects, bridge model with LRB and additional dampers were tested, and the pounding effects under various earthquake wave input were discussed as well. The test data for the model can been converted to prototype using the theory of small scaled models and has been applied in seismic design of bridge. The following conclusions can be drawn:
(1) The peak acceleration of the girder with LRB is smaller compared with rubber bearing under same earthquake wave input. The LRB significantly reduced the relative displacement and the pounding force compared with the conventional rubber bearing.
(2) The pounding force and times can be decreased by additional dampers. Seismic responses mitigation of additional dampers are closely related to the spectral characteristics of ground motion and dynamic properties of bridge structures, so it is necessary to optimize parameters of the dampers when using additional damper as passive dissipation devices for bridge structures.
(3) The traveling wave effect is major factor on seismic pounding response of elevated bridges. Seismic pounding effect of superstructures may increase or decrease obviously under traveling wave excitation. If traveling wave effects are ignored, the maximum pounding force may be underestimated, it can be crucial for the design point of view.
(4) Seismic pounding effect of bridge superstructures is dependent on the different structural dynamic properties of the adjacent girders and different characteristics of ground motions at the multi-supports along the bridges.
References
-
Han Q., Du X. L., Zhou Y. H., Lee George C. Experimental study of hollow rectangular bridge column performance under vertical and cyclically bilateral loads. Earthquake Engineering and Engineering Vibration, Vol. 12, Issue 9, 2013, p. 433-445.
-
Han Q., Du X. L., Liu J. B., et al. The seismic damage of highway bridges during 2008 Wenchuan earthquake. Earthquake Engineering and Engineering Vibration, Vol. 8, Issue 2, 2009, p. 263-273.
-
Kiureghian A. D. A coherency model for spatially varying ground motion. Earthquake Engineering and Structure Dynamics, Vol. 25, Issue 1, 1996, p. 99-111.
-
Nielson B., DesRoches R. Seismic performance assessment of simply supported and continuous multi-span concrete girder highway bridges. Journal of Bridge Engineering, Vol. 12, Issue 5, 2007, p. 611-620.
-
Padgett J. E., DesRoches R. Three-dimensional nonlinear seismic performance evaluation of retrofit measures for typical steel girder bridges. Engineering Structures, Vol. 30, Issue 7, 2008, p. 1869-1878.
-
Shinozuka M., Feng M. Q. Mitigation of seismic pounding effect on bridges using dynamic restrainers. Damping and Isolation, Vol. 13, Issue 2, 2000, p. 377-387.
-
Wang C. J. Failure study of a bridge subjected to pounding and sliding under severe ground motions. International Journal of Impact Engineering, Vol. 34, Issue 2, 2007, p. 216-231.
-
Shehata Abdel Raheem E. Pounding mitigation and unseating prevention at expansion joints of isolated multi-span bridges. Structures Engineering, Vol. 31, Issue 10, 2009, p. 2345-2356.
-
Jankowski R., Wilde K., Fujino Y. Pounding of superstructure segments is isolated elevated bridge during earthquakes. Earthquake Engineering and Structural Dynamics, Vol. 27, Issue 5, 1998, p. 487-502.
-
Chau K. T., Wei X. X. Pounding of structures modeled as non-linear impacts of two oscillators. Earthquake Engineering and Structural Dynamics, Vol. 30, Issue 5, 2001, p. 633-651.
-
Jankowski R. Non-linear viscoelastic modeling of earthquake-induced structural pounding. Earthquake Engineering and Structural Dynamics, Vol. 34, Issue 6, 2005, p. 595-611.
-
Muthukumar S., DesRoches R. Effect of pounding and restrainers response of multiple-frame bridges. Journal of Structural Engineering, Vol. 128, Issue 7, 2002, p. 860-869.
-
Muthukumar S., DesRoches R. A hertz contact model with non-linear damping for pounding simulation. Earthquake Engineering and Structural Dynamics, Vol. 35, Issue 7, 2006, p. 811-828.
-
Lopez-Garcia D., Soong T. T. Evaluation of current criteria in predicting the separation necessary to prevent seismic pounding between nonlinear hysteretic structural systems. Engineering Structures, Vol. 31, Issue 7, 2009, p. 1217-1229.
-
Dimitrakopoulos E., Makris N., Kappos A. J. Dimensional analysis of the earthquake-induced pounding between adjacent structures. Earthquake Engineering and Structural Dynamics, Vol. 38, Issue 7, 2009, p. 867-886.
-
Yeh Y. K., Mo Y. L., Yang C. Y. Seismic performance of rectangular hollow bridge columns. Journal of Structural Engineering, Vol. 128, Issue 1, 2002, p. 60-68.
-
Pinto A. V., Molina J., Tsionis G. Cyclic tests on large-scale models of existing bridge piers with rectangular hollow cross-section. Earthquake Engineering and Structural Dynamics, Vol. 32, Issue 13, 2003, p. 1995-2012.
-
Calvi G. M., Pavese A., Rasulo A., et al. Experimental and numerical studies on the seismic response of R.C. hollow bridge piers. Bulletin of Earthquake Engineering, Vol. 3, Issue 1, 2005, p. 267-297.
-
Li Z. X., Zhang Y., Yue F. Q. Shaking table test on pounding responses of simply supported isolated bridges under earthquake excitation. Earthquake Engineering and Engineering Dynamics, Vol. 27, Issue 2, 2007, p. 152-157.
-
Johnson N., Ranf T., Saiidi M. Seismic testing of a two-span reinforced concrete bridge. Journal of Bridge Engineering, Vol. 13, Issue 2, 2008, p. 173-182.
-
Cruz C. A., Saiidi M. Shake-table studies of a four-span bridge model with advanced materials. Journal of Structural Engineering, Vol. 138, Issue 2, 2012, p. 183-192.
About this article
This research is jointly funded by Beijing Natural Science Foundation (No. 8122003), the National Natural Science Fund of China (Grants No. 51478022), the Research Project of Beijing Municipal Commission of Education (Grant No. KZ201410005011), and Program for Changjiang Scholars and Innovative Research Team in University (Grant No. IRT13044). Their supports are gratefully acknowledged.
