Abstract
This paper proposes a stochastic MFBD (maintenance function block diagram) to describe fault diagnosis dynamic behavior of availability fluctuation evaluation for complex electromechanical system, which considers comprehensive diagnostic parameters, maintenance process and resource. The availability evaluation of complex electromechanical systems is achieved by simulation method. Firstly, the faults are divided into several types according to the quantity relationship represented by testability parameters and the logic sequence of fault-related activities is modeled. Math models describing the uncertainty between activities are established, which are embedded within MFBD. The stochastic MFBD is transformed into a simulation model designed via PI (process interaction) algorithm. Finally, a discrete-event simulation example for availability analysis of complex electromechanical system is provided and the accuracy and applicability of the proposed method are verified.
1. Introduction
Complex electromechanical systems are dynamic and nonlinear systems that exhibit complex dynamic behaviors. And the subsystems like mechanical transmission devices, signal control software and so on suffer from degradation process. Instantaneous availability is comprehensive reflection of effect of health monitoring and intelligent diagnosis in complex systems. However, with the requirement of high reliability and long-life, testability design and fault diagnosis factors are considered in the design process of complex electromechanical systems which leads to availability fluctuation. Due to the scale and complexity of the system structure, the description and solution of availability model become very difficult. Thus, a proper way to evaluate the availability of complex system with testability parameters is necessary. Simulation which is researched a lot is an appropriate method.
So far, a lot of researches on process simulation modeling have been performed. As the maintenance process supporting the system operations is complex, tools such as modeling and simulation are helpful to understand the interactions within it. Discrete-event simulation is an efficient methodology to predict availability for a wide range of system designs, including time-dependent systems with multiple states, dependencies among non-perfect maintenance policies [1]. Vincent L. et al. proposed constraint programming approach for the steady-state simulation of complex systems [2-4]. Zhou R. et al. used agent-based simulation technology to establish maintenance process model and to solve complex system reliability [5-7]. Chew S. P. et al. utilized PNs as the model of equipment’s maintenance task process for the virtual maintainability analysis and maintenance training [8-12]. In addition, a variety of simulation tools, like Logistics Composite Model (LCOM) were used for logistics and supply chain analysis and requirements building [13-15].
Most previous studies didn’t consider effect of comprehensive diagnostic parameters on the design of complex electromechanical systems in the model and simulation. Meanwhile, there were some problems in the description and solution of diagnostic and maintenance process. Thus, the stochastic MFBD method is used to describe dynamic behavior in complex electromechanical systems based on FBD. FBD model is used for function analysis when the process has a lot of details [16-20]. Moreover, if stochastic MFBD is used as the simulation model to evaluate system performance, the results of O&MTA can be easily filled as the attributes of each maintenance block. Stochastic MFBD describes the system from the view of function and helps technicians to make out logic sequence and hierarchical relationships of maintenance tasks from the top level of system to the bottom level of components [21].
This paper proposes a stochastic MFBD on the basis of FBD to describe macro dynamic process of fault diagnosis in complex electromechanical systems. The availability evaluation of complex electromechanical systems is achieved by simulation method.
The remainder of this paper is organized as follows: in Section 2, faults occurred in CM processes are divided into several types and specified activities for them are analyzed. Section 3 establishes six math models expressing the uncertain relationship between CM activities, and the stochastic MFBD is then constructed. In the fourth section, a simulation software structure is provided, and the process interaction algorithm is selected as the simulation strategy. In the fifth section, a simulation example of maintenance for a complex system is studied, availability and MCR (mission capable rates) of which are obtained and verified. In the sixth section, conclusions are addressed based on the above analysis and further work is put forward.
2. Corrective maintenance model
2.1. Overview of the corrective maintenance process
The corrective maintenance process can be divided into FD (fault detection), FI (fault isolation), and maintenance in sequence, which can be further described in specified details for different fault types. The detailed CM processes for different types of faults are depicted in the following steps:
Step 1: The fault signal is usually produced during the fault detection process. Fault detection is usually executed by BITE (built in test equipment) or expert with enough experience (which we call “artificial” method). However, the alarmed fault detected by BITE sometimes may be false, and this kind of fault is so-called “false-alarm”. So there are two kinds of fault called “false-alarm” and “true-alarm”.
Step 2: If the fault is true, this fault may be detected by BITE or artificial. If the fault is detected by BITE, it will be sent for BITE isolations, otherwise the system will go through artificial isolation process to locate this fault to one component; if the fault is a false-alarm, then it will go through the same steps as true faults, but the false-alarm will be found when performing the maintenance for “faulty component”.
Step 3: If the fault is detected by BITE, the system with fault signal will go through the fault isolation process to isolate this fault to one specified component. In ideal condition, the fault component can be obtained afterward. However, under some certain circumstances, only a fuzzy group in which the faulty component exists can be obtained. If the fault is isolated to a single component, faulty component will be replaced by a new one; otherwise, which component is faulty should be firstly checked out according to the following methods: considering the possibility of component failures, the failure-prone component should be detached and checked before the more reliable units. This helps to find fault more rapidly and decreases the number of unnecessary test operations.
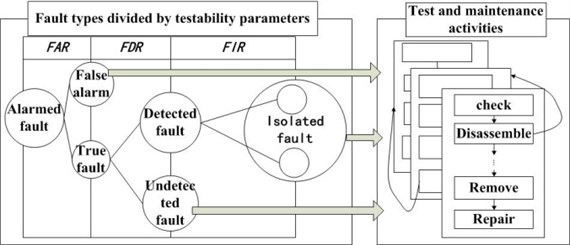
From the detailed CM process above, we select three parameters to describe the numerical relationship of different kinds of faults. They are false alarm rate (FAR), fault detection rate (FDR) and fault isolation rate (FIR). FAR expresses the relationship of the false-alarms and the alarmed faults. FDR expresses the relationship of the detected faults and the true-faults. FIR expresses the relationship of the faults can be isolated to fuzzy group with ambiguity and the detected faults. Relationship of these three parameters determines the fault types, and obviously, CM processes for different fault types will be further influenced by the testability parameters. Relationships of fault types determined by testability parameters and CM processes were shown in Fig. 1.
Fig. 1Relationship of fault types determined by testability parameters and CM process
2.2. Stochastic maintenance functional block diagram
The relationships of complex maintenance tasks not only consist of logic sequence but also hierarchical structure. If one of many succeeding tasks is chosen to be accomplished after one function, the task will be determined by the certain extent of the function result. When the simulation is conducted on the basis of stochastic MFBD, the extent should be quantified to facilitate the determination of succeeding task. In order to solve this problem, the extent of function result is related to system design parameters and some testability parameters. These design parameters are then injected into stochastic MFBD to express randomness.
2.3. Math models
In this part, we purpose math models to describe CM. According to step 1 in section 2.1, the fault alarm may come either from BITE or artificial methods, then the probability of the above event can be calculated in fault detection model.
A binary variable is used to express whether the alarm is detected by BITE or artificial methods. The variable is equal to 1 if the method is BITE. Otherwise is 0.
The probability density function of can be calculated by the number relationship of different kinds of faults. The value of is determined by ratios of corresponding alarm numbers to the sum of fault alarms. The calculation methods are shown in Eqs. (1), (2):
To convert the fault number relationships to testability parameters, we get the last form of equations as above. Eqs. (3), (4) converts the fault number relationships to testability parameters:
Taking Eq. (1) and Eq. (4) into consideration can be calculated by Eq. (5):
The integrated function of x can be expressed as follows:
Another five math models, false-alarm model, fault isolation and replace model and so on are presented in the same way as fault detection model.
2.4. Simulation models
Combining with Step 3 and Math Model, the stochastic MFBD expressing the fault isolation and replacement process can be constructed as shown in Fig. 2. Stochastic selection criteria for activities can be obtained from the method previous. The simulation models of fault detection and fault alarm are similar to this model and are omitted.
Fig. 2Fault isolation maintenance functional diagram block
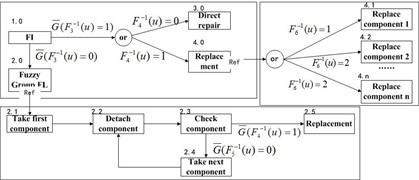
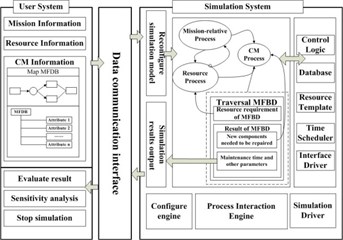
Fig. 3Main procedure of simulation and structure of simulation software
3. Simulation algorithm
3.1. Software structure
The software is composed of three subsystems, user system, data communication interface and simulation system. Users input parameters and get the simulation results by user subsystem which also shows some related information. Simulation subsystem is responsible for main process of simulation. The main procedure of simulation and structure of this simulation software is shown in Fig. 3.
3.2. Process interaction algorithm
Maintenance systems have a well-defined process, which can be captured using a discrete event simulation (DES) model. The equipment and components are modeled as simulation objects with characteristics such as a descriptive name, the time in operation, and a flag indicating whether a part is broken or not. PI is designed to describe the entity behavior without the need to establish the relationships of large amounts of events, characteristics of maintenance process that aim at describe entity-equipment behavior in its lifecycle. This simulation algorithm involves mission process, mission preparation process, mission turnaround process, CM process and resource process. Therefore, PI was selected as the simulation strategy.
4. Simulation case study
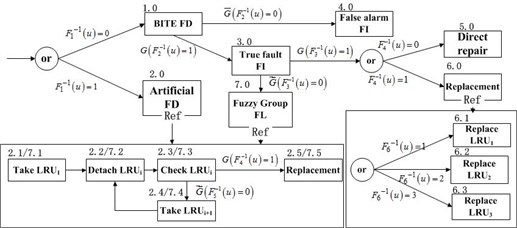
There is one unit composited of ten electromechanical systems and each system is consisted of two control and monitoring unit (ACE1 and ACE2), two actuators and right aileron which correspond to ID in Table 1. Replaceable units group in the system was (LRU1, LRU2 and LRU3), and the fuzzy group in the system was (LRU1, LRU2, LRU4). There was no component group or fuzzy group in the 6 kinds of LRUs. Mission lasting time of this electromechanical system unit was 365 days. There were three kinds of maintenance sites: local site, central and factory. The testability parameters, FAR, FDR and FIR are 0.05, 0.90 and 0.90, respectively. FDT is 5 min and FIT is 10 min. The MFBD embedded with testability parameters was expressed in Fig. 4. Electromechanical system configuration data were shown in Table 1.
Fig. 4Maintenance functional block diagram on system level
Because the testability design of equipment would affect the availability of equipment and the results evaluating the testability design influence on the above factors were shown. The availability trends were shown in Fig. 5. As shown in the figures, if the FDR was increased from 0.90 to 0.95, the availability would be increased from 0.77 to 0.83. However, testability parameter which had the greatest impact on the availability was FAR. If the FAR was reduced, the availability would increase a lot from 0.77 to 0.9.
Table 1Time of direct maintenance and replacement and spare configuration of each site
Name | ID | Direct (min) | Replace (min) | Distribution | Local | Central | Factory |
System | 30 | 25 | exp | ||||
ACE1 | LRU1 | 50 | 20 | exp | 1 | 1 | 3 |
ACE2 | LRU2 | 40 | 15 | exp | 4 | 2 | 8 |
Actuators1 | LRU3 | 45 | 18 | exp | 6 | 1 | 9 |
Actuators2 | LRU4 | 20 | 20 | exp | 3 | 8 | 6 |
Right aileron | LRU5 | 10 | 12 | exp | 5 | 3 | 2 |
Fig. 5Availability comparison by enhancing FDR and FAR
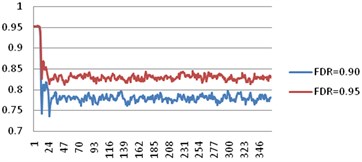
a)
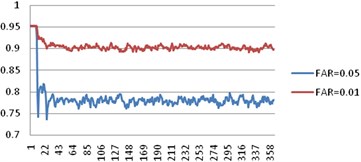
b)
5. Conclusions
This paper proposes a stochastic MFBD based on FBD to describe macro dynamic process of fault diagnosis in complex electromechanical systems, which was exemplified and validated in the example of an availability study of a complex system. In this study, the model considers comprehensive diagnostic parameters, maintenance process and resource. It turned out that the stochastic MFBD modeling method is convenient and applicable in engineering practices. Extensions of this work could be related to testability design aspects of the complex system in order to increase the assessed availability. For instance, more RMS design parameters should be incorporated in stochastic MFBD to represent the model stochastic uncertainty.
References
-
Faulin J., Juan A. A., Serrat C., Bargueno V. Predicting availability functions in time-dependent complex systems with SAEDES simulation algorithms. Reliability Engineering and System Safety, Vol. 93, Issue 11, 2008, p. 1761-1771.
-
Larroudé V., Chenouard R., Yvars P. A., Millet D. Constraint based approach for the steady-state simulation of complex systems: Application to ship control. Engineering Applications of Artificial Intelligence, Vol. 26, Issue 1, 2013, p. 499-514.
-
Chen Zhicheng, Lu Yao, Jianjun Yang Effective availability simulation evaluation research on complex ship system. International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, 2013.
-
Zhang L. Study on simulation technology of complex mechanics product. Mechanical and Electrical Engineering Magazine, Vol. 24, Issue 10, 2007, p. 67-70.
-
Zhou R., Fox B., Lee H. P., Nee A. Y. C. Bus maintenance scheduling using multi-agent systems. Engineering Applications of Artificial Intelligence, Vol. 17, Issue 6, 2004, p. 623-630.
-
Kaegi M., Mock R., Kroger W. Analyzing maintenance strategies by agent-based simulations: A feasibility study. Reliability Engineering and System Safety, Vol. 94, Issue 9, 2009, p. 1416-1421.
-
Jun-Hai Cao, Xiao-Long Chen, Ying Shen Multi-level reliability states analysis mothed in agent-based complex system reliability simulation. International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, 2013.
-
Chew S. P., Dunnett S. J., Andrews J. D. Phased mission modelling of systems with maintenance-free operating periods using simulated Petri nets. Reliability Engineering and System Safety, Vol. 93, Issue 4, 2008, p. 980-994.
-
Jin G. Dynamic system reliability modeling and simulation of high reliability systems. National University of Defense Technology, 2000.
-
Vitali Volovoi System-level maintenance policies via stochastic petri nets with aging tokens. Ph. D., Georgia Tech., Atlanta.
-
Jianbin He, Qunxing Su, Pengyuan Liu Modeling and analysis of equipment virtual maintenance process based on extended petri net. Proceedings of the International Forum on Information Technology and Applications, Washington, USA, 2009, p. 181-184.
-
Zouakia Rochdia, Bouami Drissb, Tkiouat Mohamedc Industrial systems maintenance modelling using Petri nets. Reliability Engineering and System Safety, Vol. 65, Issue 2, 1999, p. 119-124.
-
Gossard T., Brown N., Powers S., Crippen D. Scalable integration model for objective resource capability evaluations. Simulation Conference Proceedings, Winter, 1999.
-
Adam MacKenzie, Miller J. O., Raymond R. Hill, Stephen P. Chambal Application of agent based modelling to aircraft maintenance manning and sortie generation. Simulation Modelling Practice and Theory, Vol. 20, Issue 1, p. 89-98, 2012.
-
Rossetti M. D., Thomas S. Object-oriented multi-indenture multi-echelon spare parts supply chain simulation model. International Journal of Modelling and Simulation, Vol. 26, Issue 4, p. 359-362, 2006, p. 364-369.
-
Wendell Q. Lamas, Jose L. Silveira, Giorgio E. O. Giacaglia , Luiz O. M. Reis Development of a methodology for cost determination of wastewatertreatment based on functional diagram. Applied Thermal Engineering, Vol. 29, Issue 10, 2009, p. 2061-2071.
-
Sheng-He Wang, Mi-Ching Tsai Dynamic modeling of thickness-mode piezoelectric transducer using the block. Ultrasonics, Vol. 51, Issue 5, 2011, p. 617-624.
-
Tsai Y. T., Hsu Y. Y. A study of function-based diagnosis strategy and testability analysis for a system. Journal of Mechanical Engineering Science, Vol. 226, Issue 1, 2011.
-
Ioannis A. Papazoglou Functional block diagrams and automated construction of event trees. Reliability Engineering and System Safety, Vol. 61, Issue 3, 1998, p. 185-214.
-
Salvatore Distefano, Antonio Puliafito Reliability and availability analysis of dependent-dynamic systems with DRBDs. Reliability Engineering and System Safety, Vol. 94, Issue 9, 2009, p. 1381-1393.
-
Anatoly Lisnianski Extended block diagram method for a multi-state system reliability assessment. Reliability Engineering and System Safety, Vol. 92, Issue 12, 2007, p. 1601-1607.
