An analysis of the equipotential surface waves of the Earth’s gravity field

1. Introduction

Geodetic, geophysical and other measurements of the Earth’s surface are performed in relation to the Earth’s gravity field. The geodetic instruments should be leveled in order to ensure a consistency between the vertical axes of the measuring instrument and the direction of the gravity force at a point of measurements. The fact that gravity has dissimilar values and directions in different points has to be taken into account. Moreover, the surfaces of the equal gravity potential (the equipotential surfaces) have complicated shapes. So, taking the non-homogeneity of the gravity field into account, the precise measurements should be reduced to the common coordinate system, which will be used for the adjustments of the measurements. In order to estimate the non-homogeneity of the gravity field, gravimetric observations should be executed [1].

The equipotential surfaces of the Earth’s gravity field are crucially important when detecting the heights of the points on the Earth’s surface [2, 3]. One of the equipotential surfaces is geoid, which is used to determine the geopotential heights [4, 5]. In various countries, different equipotential surfaces could be adopted for geoid models, and the various heights systems could be employed [6].

The Earth’s gravity field incessantly fluctuates and disturbs the shapes of the equipotential surfaces. As a result, it becomes difficult to select the correct geoid and to determine the heights in general. The geodynamic processes (earthquakes, erupting volcanoes, movements of continents and Earth Crust) and anthropogenic activities (development of the big water pounds, exploitation of digging materials and water) cause the fluctuations of the Earth’s gravity field [7]. The celestial bodies cause the most significant periodical fluctuations of the gravity field and its equipotential surfaces [8-10]. The attractive forces of the Moon and Sun must be taken into account. It is necessary to consider the Lunisolar effect when choosing the geoid and performing the precise geodetic measurements. However, the influence of the celestial bodies is often estimated without enough accuracy or by applying different methodologies [11, 12].

A detailed analysis is performed on the influence that the celestial bodies have on the equipotential surface of the Earth’s gravity field. The necessary background is developed in order to progress a new more intelligent methodology of estimating the influence that the celestial bodies have on the geodetic measurements. Previous studies demonstrate that this influence strongly depends on the elasticity of the solid Earth and is unequal on different equipotential surface waves [10]. It is important to investigate the different kinds of waves and their parameters. Some results of current investigations are presented, which demonstrate the waves of the Earth’s gravity field influenced by the celestial bodies.

2. The tidal potential caused by a celestial body

The tidal potential for the solid Earth is equal to the difference between the values of the attractive field (created by the celestial body at the point of measurement) on the Earth’s surface and in the Earth’s mass center:

where $G$ is the gravitational constant; $m$ is the mass of the celestial body; $r\mathrm{\text{'}}$ is the topocentric distance of the celestial body and $r$ is the geocentric distance to a point of measurements.

It is possible to express the $1/r\mathrm{\text{'}}$ by a series of spherical functions in the form of a series of the tidal potential [10]:

where $R$ is the geocentric distance of the point on the Earth’s surface; $z$ is the geocentric zenith distance of the celestial body; $P_n\left(\mathrm{c}\mathrm{o}\mathrm{s}z\right)$ is the Legendre polynomials in the range [–1; +1].

In order to investigate the fluctuations of the gravity field’s equipotential surfaces, a new expression is applied. Here, the tidal potential containing equatorial coordinates is used instead of horizontal coordinates [10, 13]:

where $\mathrm{\Phi }$ is the geocentric latitude of the point on the Earth’s surface; $\delta$ is the declination of the celestial body; $t$ is the local hour angle of the celestial body; $P_n^k\left(\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{\Phi }\right)$, $P_n^k\left(\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{\delta }\right)$ are appended Legendre functions.

3. The waves of the equipotential surface

The fluctuation of the equipotential surface of the Earth’s gravity field, caused by the influence of a celestial body, can be expressed by the following formulae:

where $g$ is the value of gravity.

According to investigations [13], only the first three members of the tidal potential series can be used when estimating the influence that the Moon and the Sun have on the equipotential surface of the Earth’s gravity field. Using the Eq. (3), the formulas of these three members yield. They express the fluctuations of the equipotential surface caused by the celestial body to real Earth:

where ${\gamma }_n=1+k_n-h_n$ is the Earth’s elasticity coefficient; $k_n$ and $h_n$ are Love numbers [14].

From the Eqs. (5)-(7), it can be observed that the effect of the celestial body depends on the latitude $\mathrm{\Phi }$ and the hour angle of the celestial body, which is related to the longitude. Therefore, concurrently, the effect of the celestial body is different in various parts of the Earth.

It should be noted, that the first members of the Eqs. (5)-(7) do not depend on local hour angle of the celestial body. They are rather the long period waves, which depend on the local latitude and the declination of the celestial body. They are the zonal waves. The period of other waves changes from one day to a part of a day. These are the tesseral‎ and sectorial waves.

4. An analysis of the zonal waves

In this section, the influence that the celestial bodies have on the zonal waves is analyzed. According to Eqs. (5)-(7), formulae yields, which represent the zonal waves of the equipotential surface of the gravity field:

where:

Taking into account that the declination of the Moon could be in the interval from –28°35’ to +28°35’, and the declination of the Sun could be from –23°26’ to +23°26’, the graphics of the functions $K\left(\delta \right)$ look as it is shown in the Fig. 1.

Fig. 1The graphics of the functions K(δ)

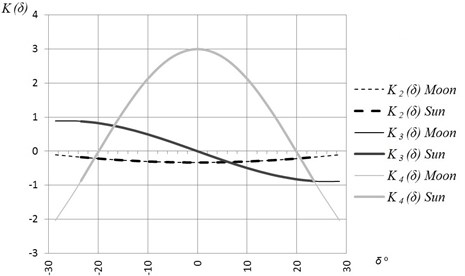
It is observed that the maximal values of functions $K_2\left(\delta \right)$ and $K_4\left(\delta \right)$ yield at the moment when the declination of the celestial body is equal to zero, and when coefficients are equal to 0.333 and 3.0 correspondingly. The range of the function $K_2\left(\delta \right)$, due to the parameters of the Moon, is 0.229; due to the parameters of the Sun, is 0.158. The range of the function $K_4\left(\delta \right)$, due to the parameters of the Moon, is 5.033; due to the parameters of the Sun, is 3.869. The character of the function $K_3\left(\delta \right)$ is slightly different. The maximal value of the function yields at the moment when the values of the declinations of the celestial bodies are maximal. The range of the function is 1.775 (due to the Moon) and 1.757 (due to the Sun).

The Eq. (8) and the graphics of functions $K_2\left(\delta \right)$, $K_3\left(\delta \right)$ and $K_4\left(\delta \right)$ demonstrate that the fluctuation of the equipotential surface is highest when the declinations of the celestial bodies are equal to 0°. The dependence of the zonal wave of the equipotential surface from the latitude and declination is shown in the Fig. 2.

Fig. 2The dependence of the zonal wave of the equipotential surface from the latitude and declination

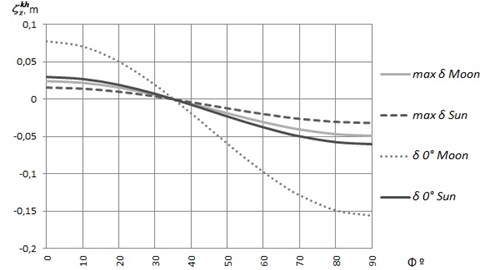
Fig. 2 demonstrates that, due to the influence of the Moon, the equipotential surface rises to 7.78 cm at the equator. Moreover, it rises to 2.99 cm due to the influence of the Sun. At the poles, the equipotential surface goes down to 15.57 cm (due to the influence of the Moon) and to 5.99 cm (due to the influence of the Sun). The highest range of deformation, caused by the effect of the Moon, is 23.35 cm; and, caused by the effect of the Sun, is 8.98 cm (when the declinations of the celestial bodies are equal to 0°). When the declinations of the celestial bodies are maximal, these ranges are 7.31 cm and 4.72 cm respectively.

Calculations are performed using the following values of the celestial bodies and their movements: selenocentric gravitational constant $G_{mM}=\text{4902}\text{.}\text{799 km}\text{3}\text{s}\text{-2}\text{;}$ heliocentric gravitational constant $G_{mS}=\text{132 712 440 018 km}\text{3}\text{s}\text{-2}$; the minimal geocentric distance to the $\text{Moon}\text{=}\text{356400 km}$, and to the $\text{Sun = 147098074 km}$; the average value of gravity acceleration $g=\text{980665 mGal}$; the average geocentric distance to a point on the Earth’s surface $R=\text{6371 km}$.

Functions, which depend on $\delta$, could be estimated by accepting their average integral values [12]. The zonal waves of the equipotential surface yield:

where:

where $\epsilon$ is the angle between the equator of the celestial sphere and the plane of the celestial body orbit.

The angle between the equator of the celestial sphere and the plane of the Moon orbit can vary from 18°17’ till 28°35’. The period of change is 18.6 years. The angle between the equator of the celestial sphere and the ecliptic is 23°26’. Calculations present the following values of the function $K\left(\epsilon \right)$: $K_2{\left(\epsilon \right)}_{Sun}=$–0.763, $K_4{\left(\epsilon \right)}_{Sun}=$–0.879. Due to the Moon, $K_2\left(\epsilon \right)$ changes from –0.852 to –0.657; $K_4\left(\epsilon \right)$ changes from –0.562 to –1.163. The graphic of the function ${\mathrm{\zeta }}_{zv}^{kh}$ is shown in the Fig. 3.

Fig. 3The graphic of the function ζzvkh

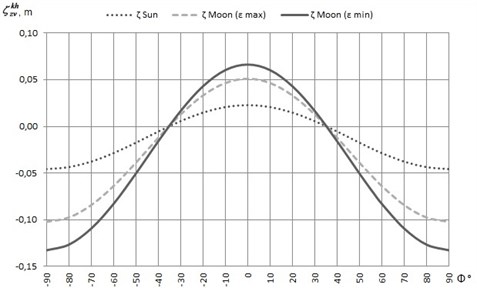
At the equator, the equipotential surface rises to 6.64 cm due to the influence of the Moon; it rises to 2.27 cm due to the influence of the Sun. At the poles, the equipotential surface goes down till 13.27 cm due to the Moon’s influence and till 4.57 cm – due to the Sun’s influence. For example, in the southern part of Lithuania, due to the Moon’s influence, the equipotential surface goes down to 6.24 cm and to 2.15 cm due to the Sun’s influence. In the northern parts of Lithuania, these parameters are 7.13 and 2.46 correspondingly.

In the second and fourth zonal waves, it is possible to distinguish the permanent fluctuations of the equipotential surface, which depend only on the latitude:

The graphic of the function Eq. (15) is shown in Fig. 4.

Fig. 4The graphic of the function ζzΦkh

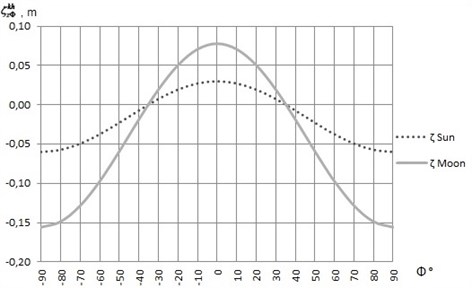
Fig. 4 presents that at the equator, due to the Moon’s influence, the equipotential surface rises to 7.79 cm. Due to the influence of the Sun, it rises to 2.99 cm. At the poles, the equipotential surface goes down to 15.57 cm (due to the Moon’s influence) and to 5.99 cm (due to the Sun’s influence). For example, in the southern part of Lithuania, due to the Moon’s influence, the equipotential surface goes down to 7.32 cm. Due to the impact of the Sun, it goes to 2.81 cm. In the northern parts of Lithuania, these parameters are 8.37 and 3.22 correspondingly. Presented analysis of zonal tidal waves can be used to determine what equipotential surface (affected or not affected by the zonal wave) has to be accepted as the geoid.

5. The amplitudes of the non-zonal waves

From Eq. (5)-(7), three non-zonal waves can be distinguished. They differ by their periods. Formulas for the amplitudes of these waves yield:

The graphics of Eq. (16)-(19) are shown in Figs. 5 and 6.

Fig. 5 demonstrates that the maximal amplitudes of the function $A_1$ are (1) when the points on the Earth’s surface are in the middle latitudes; (2) when the declinations of the celestial bodies have maximal values; (3) when the deformation of the equipotential surface reaches 19.59 cm (due to the impact of the Moon) and 4.50 cm (due to the impact of the Sun). At the poles, due to the Moon’s influence, the equipotential surface goes down to 15.57 cm. Due to the impact of the Sun, it goes to 5.99 cm. For example, in the southern part of Lithuania, the equipotential surface goes down to 7.32 cm (due to the Moon’s influence) and to 2.81 cm (due to the influence of the Sun). In the northern parts of Lithuania, these parameters are 8.37 and 3.22 correspondingly. The maximal amplitudes of the function $A_2$ are on equator, when the declinations of the celestial bodies equal to 0°, and the deformation of the equipotential surface reaches 23.35 cm (due to the Moon’s influence) and 8.99 cm (due to the Sun’s influence). At the points of the average latitude of the Lithuanian territory, the values of the function $A_1$ reach 18.32 cm (due to the Moon’s influence) and 4.22 cm (due to the Sun’s influence). The values of the function $A_2$ are 7.70 cm (due to the impact of the Moon) and 2.97 cm (due to the impact of the Sun).

Fig. 5The amplitudes of the non-zonal waves A1 and A2

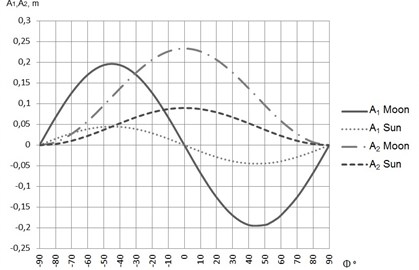
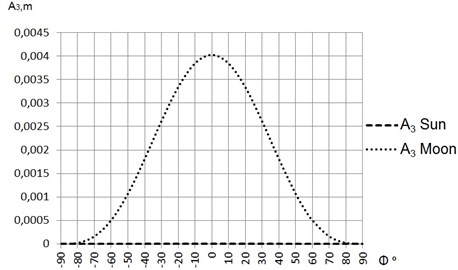
The maximal values of the function $A_3$ are at the equator, when declinations of the celestial bodies are equal to 0°, and the deformation of the equipotential surface, due to the Moon’s influence, reaches 0.40 cm. The deformation of the equipotential surface due to the Sun is negligible. Values of functions $A_3$ and $A_4$ reach few hundreds parts of a millimeter only.

Fig. 6The amplitudes of the non-zonal waves A3

6. The selection of a geoid

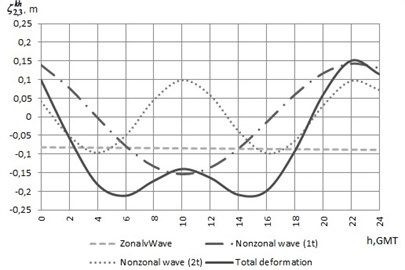
A geoid, as an equipotential surface of the gravity field from which the orthometric heights are defined, plays an important role in the systems of the geopotential heights. However, the problematic question of how to assess the influence of the Moon and Sun on the deformations of the geoid surface remains unanswered. There are two possibilities in the estimation procedure: to either eliminate the influence or to reconstruct it. From the presented investigations, there are three options to reconstruct the values of the permanent zonal waves, according to Eqs. (8), (12) or (15). At the points of average latitude (54.5°) of the Lithuanian territory, the values of the zonal wave, periodical waves and total deformation during one day are shown in the Fig. 7. The chosen day is the 30th of January 2014, when the distance to the Moon is minimal and syzygy takes place.

Fig. 7 demonstrates that the range of the deformations of the equipotential surface reaches 36.27 cm during the day. At the same time, the speed of the surface deformations is saltatory. During the day, the surface goes down about 8.57 cm due to zonal wave and changes to 0.70 cm marginally. Also, it should be noted that non-zonal waves have the diurnal and semidiurnal periods.

Fig. 7The graphics of the zonal wave, periodic waves and total deformation

7. Evaluation of the effect of celestial bodies in Lithuania’s first geodetic vertical network

Equipotential surface deformations, induced by the celestial bodies, can change height differences between points on the Earth’s surface. It is therefore necessary to evaluate these changes accurately.

6

Fig. 8Results of the evaluation of celestial bodies effect

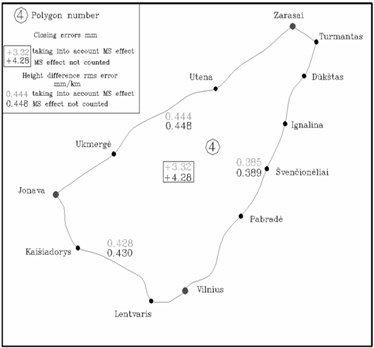
For the vertical network lines (Fig. 8) in the 4th polygon of the first class vertical network of Lithuania, the root mean square error values of the height differences for one km length line are calculated. Calculations are done according to the misalignments of height differences, measured in direct and reverse directions. The calculations are done both when the effect of the celestial bodies is taken into consideration, and when the effect of the celestial bodies is not assessed [3].

While carrying out the analysis of errors, it appeared that, after the evaluation of the Lunisolar effect, the error for the lines of the experimental polygon tends to be smaller. The maximum reduced value of the error is 0.004 mm/km. Besides that, the closing error of the differences of heights proves to be smaller.

8. Conclusions

1. The dependence of the zonal waves of the deformations of the Earth gravity field’s equipotential surface from the local latitude and a declination of the celestial body is analyzed. It is detected that the highest waves are at the moment in time when the declination of the celestial body is equal to 0°. At the poles, the equipotential surface goes down to –15.57 cm (due to the impact of the Moon) and to –5.99 cm (due impact of the Sun). At the equator, the equipotential surface rises to +7.78 cm (due to the impact of the Moon) and to +2.99 cm (due to the impact of the Sun). At the latitudes of about 35°, the amplitude of the zonal wave is near zero. The influence of the celestial body on the deformations of the equipotential surface is highest at the poles. The amplitude of the zonal wave reaches 23.35 cm (due to the impact of the Moon), and 8.98 cm (due to the impact of the Sun).

The dependence between the zonal wave and latitude is investigated. At the equator, the equipotential surface rises to 7.79 cm (due to the impact of the Moon) and to 2.99 cm (due to the impact of the Sun). At the poles, the equipotential surface goes down to 15.57 cm (due to the impact of the Moon) and to 5.99 cm (due to the impact of the Sun). In the northern part of Lithuania, the equipotential surface goes down to 8.37 cm (due to the impact of the Moon) and to 3.22 cm (due to the impact of the Sun).

The amplitudes of the non-zonal waves of the equipotential surface are estimated. The maximal amplitudes are on the equator and reach 23.35 cm (due to the impact of the Moon) and 8.99 cm (due to the impact of the Sun). At the points of average latitude of the Lithuanian territory, the amplitudes reach 18.32 cm (due to the impact of the Moon) and 4.22 cm (due to the impact of the Sun).

The presented analysis can be used to (1) estimate the possible influence that celestial bodies have on geodetic measurements; (2) determine what equipotential surface has to be accepted as a geoid for the determination of geopotential heights.