MED and WPT based technique for bearings fault detection

2.1. Auto-selection of filter length for MED

The fundamental idea of MED is to construct an inverse filter that counteracts the effect of the transmission path, by assuming that the original excitation was impulsive and having high kurtosis [8].

Fig. 1Illustration of the MED processes

Fig. 1 shows the basic process of the MED. If a bearing operates with fault, impulses $s\left(n\right)$ are generated. $s\left(n\right)$ transmits through other machinery parts to the sensors. The transmission effect on this signal can be denoted by a filter $h$. Some noises $v\left(n\right)$ will also add into the raw impulse $s\left(n\right)$. Assume that $d\left(n\right)$ is the observed signal from sensor, and $x\left(n\right)$ is the output of MED filter $f$. The effect of the inverse filter $f$ is to recover the original impulse $s\left(n\right)$, and this process is implemented though calculating the optimal set of filter coefficients by maximizing the kurtosis of$x\left(n\right)$.

Given the output signal $x\left(n\right)$, $n=$1, 2,..., $N$, where $N$ isthe number of data samples, the MED filter $f$ can be modeled as a finite impulse response filter with $L$ coefficients such that:

The MED filters have been adopted in some machinery defect detection applications such as in the gears systems [9] and bearing condition monitoring [1]. However, the filter length, which is the most important parameter in the MED, is usually realized by trail and error, which may limit its effectiveness in real-world applications with time-varying operating conditions.

As for bearings fault detection, after MED with suitable filter length, the fault information should be highlighted and the envelope spectra should be sparse [10]. Sparsity can be expressed as follows:

where ${\Vert x\Vert }_1$ and ${\Vert x\Vert }_2$ represent the $L_1$ norm and norm $L_2$ norm off $x$, respectively.

The envelope of signal $x\left(t\right)$ can be calculated through Hilbert transform as follows:

Therefore, envelope spectra sparsity (ESS) is proposed as a measure of the MED processing. The optimal filter length $L_O$ is found to maximize this sparsity, and the method for the selection of filter length in MED is expressed in the following:

where $ME{D}_L\left(x\right)$ represent the signal obtained from the MED processing for signal $x$. The scope of the given filter length (8, 16,… to 1024) is based on the following consideration. To improve processing speed, the filter length should be an integer power of 2. If filter length is less than 8, it is not guaranteed that the output signal contains enough fault information. When the filter length is greater than 1024, it may cause a “false” impact of output signal and make diagnosis information confused.

As an example, consider a simulated bearing fault signal. The fault frequency equal to 80 Hz, the sampling frequency is 12000 Hz, resonant frequency equal to 3000 Hz. A normally distributed random noise signal with a mean of 0 and a variance of 0.6 was added to Eq. (14). The simulated signal and the mixed signal with noise are shown in Fig. 2(a) and (b), respectively. According to the proposed the index of Envelope Spectra Sparsity (ESS), the filter length is 16 and the output signal after MED is shown in Fig. 2(c). By contrast, if the filter length set to 512 under which output signal after MED has the highest kurtosis value, the output is shown in Fig. 2(d). It is seen that it is applicable to select the filter length in terms of ESS.

Fig. 2Comparison of processing results for a bearing with rolling element fault detection using the techniques of: a) the simulated signal; b) the simulated signal mixed with noise; c) output signal after MED with filter length of 16; d) output signal after MED with filter length of 512

2.2. Envelope analysis based on the optimal wavelet packet node

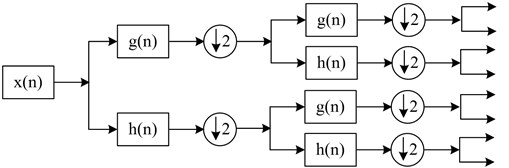
Wavelet packet transform (WPT) is an extension of discrete wavelet transform (DWT). Different from DWT, every detail signal in WPT is further decomposed into two sub-signals including an approximation signal and a detail signal, as shown in Fig. 3. For the fast algorithm, wavelet packet coefficients are calculated by [11]:

The wavelet packet child nodes ($j+1$, $2p$) and ($j+1$, $2p+1$) are derived from their parent node ($j$, $p$):

where $h\left(n\right)$ and $g\left(n\right)$ are the conjugate mirror filters for decomposition:$h\left(n\right)$ is a low-pass filter and $g\left(n\right)$ is a high-pass filter, and $\left(*\right)$ denotes convolution.

Fig. 3Wavelet packet decomposition over 3 levels

The envelope analysis is a well-known method to extract periodic impacts from the vibration signals of machinery. After using the WPT to obtain a series of nodes and selecting an appropriate node through the proposed procedure, we can proceed with the envelope analysis to extract the characteristic frequency of a bearing fault. Otherwise, for the conventional envelope analysis the first step is to perform band-pass filtering properly to enhance the bearing-fault frequency [12].

In terms of the principle of wavelet packet decomposition algorithm, the most significant bearing fault information can be reflected by wavelet packet coefficients located at one or several wavelet packet nodes at different decomposition depths.

The signal is decomposed into several WPT nodes by Wavelet packet transformation. Some nodes signals are closely related to the faults but others are not. Therefore, the most sensitive node including fault-related information should be selected from all the nodes for further envelope analysis. Considering all wavelet packet nodes at different decomposition depths, a new technique named Sparsity of Wavelet Packet Nodes (SWPN) is proposed for the fast selection of the optimal wavelet packet node and the resonant frequency band. Depending on the different sparsity values, the wavelet packet node with the highest SWPN is selected, and then an envelope analysis can be used to detect bearing faults.

2.3. The proposed fast detection method for bearing fault diagnosis

Step 1: Load an original bearing fault signal.

Step 2: Adaptive-MED. The MED is used to enhance the fault information. To make the technique automatic, Envelope Spectra Sparsity (ESS) is proposed in this paper as an indicator to select the filter length of MED.

Step 3: Wavelet packet transformation (WPT) and node selection. The signal is decomposed into several WPT nodes by Wavelet packet transformation. Sensitive nodes containing fault-related information is selected according to the proposed sparsity of wavelet packet nodes signal.

Step 4: Envelope power spectrum analysis. The power spectrum is used to highlight the bearing fault characteristic frequencies in the frequency domain.

3.1. Experimental validation through real bearing data

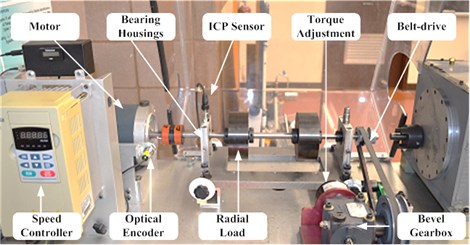
In order to verify the effectiveness of the proposed method of bearings fault detection, a lot of tests has been conducted. The experimental rig used for the effectiveness tests in this work is shown in Fig. 4. The system is driven by an induction motor, with the speed range from 20 to 3000 rpm. A variable load is enforced by a magnetic brake system through a bevel gearbox and a belt drive. An optical sensor is used to provide pulse signal for shaft speed measurement. The type of test bearing is MBER-10K. In the tests, four bearing health conditions are considered: healthy bearings, bearings with outer race defect, bearings with inner race defect and bearings with rolling element defect.

The test conditions for the following signals are as follows: shaft speed of 2100 rpm, sampling frequency of 32768 Hz, analysis data length of 1 s.

Fig. 4Experimental setup

The outer race fault characteristic frequency $f_O$, the inner race fault characteristic frequency $f_I$ and the ball spinning frequency $f_B$ are given as follow:

where $z$ is number of rolling elements, $f_R$ is shaft frequency in Hz, $\alpha$ is the contact angle. $d$ and $D$ are the diameters of the rolling element and pitch diameter, respectively. According to the above Eqs. (7)-(9), $f_O$, $f_I$ and $f_B$ are calculated as 106.75 Hz, 173.25 Hz and 139.3 Hz, respectively.

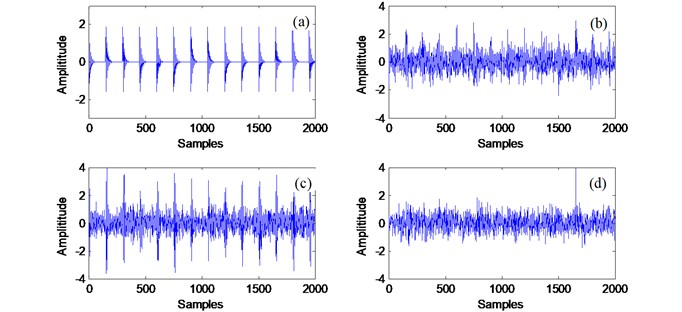
Fig. 5 shows parts of collected vibration signals as well as their corresponding spectral maps. It is seen that it is difficult to diagnose bearing operation conditions just by examining these original vibration signals and spectrum maps.

Fig. 5The vibration signal and corresponding spectral of: a) healthy bearing; b) bearing with outer race fault; c) bearing with inner race fault; d) bearing with rolling element fault

The effectiveness of the proposed bearing fault detection technique will be compared with some other related techniques. Since the proposed technique involves both auto selection parameter for MED filter and WPT processing, it will be specified as AMED-WPT for simplicity. To examine the effectiveness of the combination of MED and envelop analysis, it is designated as MED-EA. The same story, the combination of WPT and envelop analysis is specified by and WPT-EA. The commonly used envelop analysis method (designated as EA) will be compared.

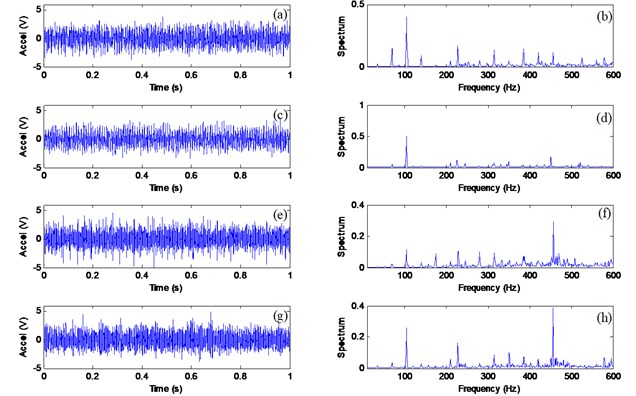
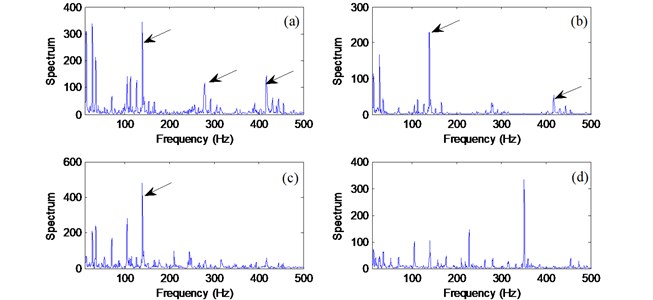
Fig. 6 shows the processing results for a healthy bearing using the related techniques. The dominant frequency component from the proposed AMED-WPT technique (Fig. 6(a)) is the 1st shaft rotation speed ($f_R=$35 Hz). Although the results from other three methods (Fig. 6(c)-(d)) show several harmonics of shaft rotation, the 1st shaft in these spectral map are not the highest peak. This may lead to an incorrect diagnosis or a false alarm, because the highest components (the third harmonic of shaft speed 105 Hz) in is very close to the outer race defect characteristic frequency ($f_O=$107.5 Hz).

Fig. 6Comparison of processing results for a healthy bearing using the techniques of: a) AMED-AWPT; b) MED-EA; c) WPT-EA; d) EA

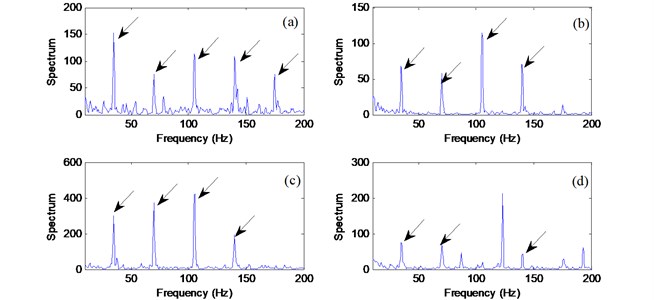
Fig. 7 illustrates processing results of the related techniques for a bearing with an outer race defect ($f_O=$107.5 Hz). It is seen that all the techniques except envelope analysis (Fig. 7(d)) can recognize the bearing fault in this case, because the resonance modes corresponding to a defect on the fixed bearing race are stable. It is showed that envelop analysis without appropriate selection of the resonant frequency band can not find the fault information. The proposed AMED-WPT technique (Fig. 7(a)) provides the highest spectral magnitude with a clear 1st to 4th harmonic due to the fault information enhancement effects from MED.

Fig. 7Comparison of processing results for a bearing with outer race fault using the techniques of: a) AMED-WPT; b) MED-EA; c) WPT-EA; d) EA

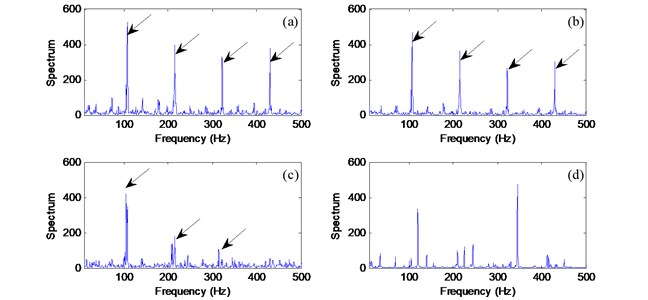
Fig. 8 shows processing results of the related techniques for a bearing with an inner race defect ($f_I=$ 173 Hz). It is same to the outrace fault detection that the first three technique can recognize the fault frequency. However, the fault frequency does not dominate in the Fig. 8(c), and other strong frequency components may result in false diagnostic result. At the same time, the spectral magnitude (Fig. 8(b)) is lower than that in (Fig. 8(a)). Based on the above analysis, the proposed AWPT technique using the MED enhancement can provide clear and best fault diagnostic information (Fig. 8(a)).

Fig. 8Comparison of processing results for a bearing with inner race fault using the techniques of: a) AMED-WPT; b) MED-EA; c) WPT-EA; d) EA

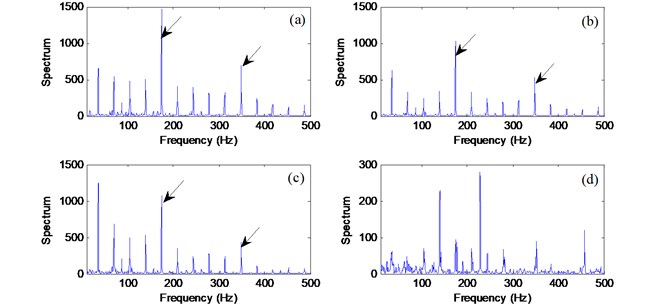
Fig. 9 illustrates processing results of the related techniques for a bearing with a rolling element defect ($f_B=$139 Hz). The diagnosis of fault for rolling elements may be the most challenging task in bearing operation condition monitoring, especially when the fault is at its initial stage. The proposed AMED-WPT technique (Fig. 9(a)) provides with a clear 1st-3rd harmonics of defect characteristic frequency. By contrast, MED-EA and WPT-EA recognize fewer harmonics.

Fig. 9Comparison of processing results for a bearing with rolling element fault using the techniques of: a) AMED-WPT; b) MED-EA; c) WPT-EA; d) EA