Jacobi pseudo-spectral Galerkin method for second kind Volterra integro-differential equations with a weakly singular kernel

Zhang, Xiaoyong; Li, Junlin

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 December 2014

Check for updates

Jacobi pseudo-spectral Galerkin method for second kind Volterra integro-differential equations with a weakly singular kernel

Xiaoyong Zhang¹

Junlin Li²

¹Shanghai Maritime University, Shanghai, China

²Taiyuan University of Science and Technology, Taiyuan, China

Corresponding Author:

Xiaoyong Zhang

Cite the article Download PDF

Downloads 1286

Abstract

The Jacobi pseudo-spectral Galerkin method for the Volterra integro-differential equations of the second kind with a weakly singular kernel is proposed in this paper. We provide a rigorous error analysis for the proposed method, which indicates that the numerical errors (in the $L_{ω_{α, β}}^{2}$ -norm and the $L^{\infty}$ -norm) will decay exponentially provided that the source function is sufficiently smooth. Numerical examples are given to illustrate the theoretical results.

1. Introduction

In practical applications one frequently encounters the Volterra integro-differential equations of the second kind with a weakly singular kernel of the form:

1

\frac{d y}{d x} = a (x) y (x) + b (x) + \int_{0}^{x} (x - s)^{- μ} K (x, s) y (s) d s, 0 < x \leq T, 0 < μ < 1 .

With the given initial condition $y (0) = y_{0}$ . Where the unknown function $y (x)$ is defined in $0 < x \leq T < \infty$ . $a (x)$ , $b (x)$ are two given source functions and $K (x, s)$ is a given kernel.

Equations of this type arise as model equations for describing turbulent diffusion problems. The numerical treatment of the Volterra integro-differential Eq. (1) is not simple, mainly due to the fact that the solutions of Eq. (1) usually have a weak singularity at $x =$ 0, as discussed in [1], the second derivative of the solution $y (x)$ behaves like $y^{2} (x) ~ x^{- μ}$ .

We point out that for Eq. (1) without the singular kernel (i.e., $μ =$ 0) spectral methods and the corresponding error analysis have been provided recently [2]; see also [3] and [4] for spectral methods to Volterra integral equations and pantograph-type delay differential equations. In both cases, the underlying solutions are smooth.

In this work, we will consider a special case, namely, the exact solutions of Eq. (1) are smooth (see also [5]). In this case, the collocation method and product integration method can be applied directly. But the main approach used there is the spectral-collocation method which is similar to a finite-difference approach. Consequently, the corresponding error analysis is more tedious as it does not fit in a unified framework. However, with a finite-element type approach, as will be performed in this work, it is natural to put the approximation scheme under the general Jacobi-Galerkin type framework. As demonstrated in the recent book of Shen etc. [16], there is a unified theory with Jacobi polynomials to approximate numerical solutions for differential and integral equations. It is also rather straightforward to derive the pseudo-spectral Jacobi-Galerkin method from the corresponding continuous version. The relevant convergence theories under the unified framework, as will be seen from Section 4, are cleaner and more reasonable than those obtained in [7].

The purpose of this work is to provide numerical methods for the second kind Volterra integro differential equations based on pseudo-spectral Galerkin methods. Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain partial differential equations (PDEs) (see e.g. [8-10] and the references therein), often involving the use of the Fast Fourier Transform. Where applicable, spectral methods have excellent error properties, with the so called ”exponential convergence” being the fastest possible.

The paper is organized as follows. In Section 2, we introduce the Jacobi pseudo-spectral Galerkin approaches for the Volterra integro-differential Eq. (3). Some preliminaries and useful lemmas are provided in Section 3. In Section 4, the convergence analysis is given. We prove the error estimates in the $L^{\infty}$ -norm and $L_{ω_{α, β}}^{2}$ -norm. The numerical experiments are carried out in Section 5, which will be used to verify the theoretical results obtained in Section 4. The final section contains conclusions.

2. Jacobi pseudo-spectral Galerkin method

In this section, we formulate the Jacobi pseudo-spectral Galerkin schemes for problem Eq. (1) For this purpose, let $ω_{α, β} = (1 - t)^{α} {(1 + t)}^{β}$ be a weight function in the usual sense, for $α$ , $β > - 1$ . $J_{k}^{α, β} (t)$ , $k = 0, 1, …,$ denote the Jacobi polynomials. The set of Jacobi polynomials ${J_{k}^{α, β} (t)}_{k = 0}^{\infty}$ forms a complete $L_{ω_{α, β}}^{2} (- 1,1)$ -orthogonal system. Before using pseudo-spectral methods, we need to restate problem Eq. (1). The usual way (see [1]) to deal with the original problem is: writing $z = b (x) + \int_{0}^{x} (x - s)^{- μ} K (x, s) y (s) d s$ , Eq. (1) is equivalent to a linear Volterra integral equations of the second kind with respect to $y$ , $z$ :

2

\{\begin{array}{l} y (x) = y_{0} + \int_{0}^{x} \{a (s) y (s) + z (s)\} d s, \\ z (x) = b (x) + \int_{0}^{x} (x - s)^{- μ} K (x, s) y (s) d s . \end{array}

For the sake of applying the theory of orthogonal polynomials conveniently, by the linear transformation:

x = \frac{T (1 + t)}{2}, s = \frac{T (1 + τ)}{2} .

Letting:

u (t) = y (\frac{T (1 + t)}{2}), w (t) = z (\frac{T (1 + t)}{2}), g (t) = b (\frac{T (1 + t)}{2}), Λ = [- 1,1],

3

\{\begin{array}{l} u (t) = y_{0} + \frac{T}{2} \int_{- 1}^{t} \{a (τ) u (τ) + w (τ)\} d τ, \\ w (t) = g (t) + {(\frac{T}{2})}^{1 - μ} \int_{- 1}^{t} (t - τ)^{- μ} K (t, τ) u (τ) d τ . \end{array}

The weak form of Eq. (3) is to find $u, w \in L_{ω_{α, β}}^{2} (Λ) \times L_{ω_{α, β}}^{2} (Λ)$ , such that:

4

\{\begin{array}{l} (u, v_{1})_{ω_{α, β}} = {(y_{0} + \frac{T}{2} \int_{- 1}^{t} \{a (τ) u (τ) + w (τ)\} d τ, v_{1})}_{ω_{α, β}}, \\ (w, v_{2})_{ω_{α, β}} = {(g (t) + {(\frac{T}{2})}^{1 - μ} \int_{- 1}^{t} (t - τ)^{- μ} K (t, τ) u (τ) d τ, v_{2})}_{ω_{α, β}}, \end{array}

\forall v_{1}, v_{2} \in L_{ω_{α, β}}^{2} (Λ) \times L_{ω_{α, β}}^{2} (Λ),

where $(., .)_{ω_{α, β}}$ denotes the usual inner product in the $L_{ω_{α, β}}^{2}$ -space.

Now, let $N$ be any positive integer and $P_{N} (Λ)$ be the set of all algebraic polynomials of degree at most $N$ . Obviously, the Jacobi polynomials $J_{0}^{α, β} (t)$ , $J_{1}^{α, β} (t)$ ,..., $J_{N}^{α, β} (t)$ are the basis functions of $P_{N} (Λ)$ .

Next, we denote the collocation points by $\{t {_{i}\}}_{i = 0}^{N}$ , which is the set of ( $N +$ 1) Jacobi Gauss point. We also define the Jacobi interpolating polynomial $I_{N}^{α, β} v \in P_{N} (Λ)$ , satisfying:

I_{N}^{α, β} v (t_{i}) = v (t_{i}), 0 \leq i \leq N .

It can be written as an expression of the form:

5

I_{N}^{α, β} v (t) = \sum_{i = 1}^{N} v (t_{i}) F (t_{i}),

where $F (t_{i})$ is the Lagrange interpolation basis function associated with the Jacobi collocation points ${\{t_{i}\}}_{i = 0}^{N}$ .

Now we describe the Jacobi pseudo-spectral Galerkin method. For this purpose, set:

τ (t, θ) = \frac{t - 1}{2} + \frac{t + 1}{2} θ, θ \in [- 1,1] .

We define that:

6

M u (t) = \frac{T}{2} \int_{- 1}^{t} a (τ) u (τ) d τ = \frac{T}{2} \int_{- 1}^{1} (\frac{t + 1}{2}) a (τ (t, θ)) u (τ (t, θ)) d θ,

7

\hat{M} u (t) = \frac{T}{2} \int_{- 1}^{t} u (τ) d τ = \frac{T}{2} \int_{- 1}^{1} (\frac{t + 1}{2}) u (τ (t, θ)) d θ,

8

\tilde{M} u (t) = {(\frac{T}{2})}^{1 - μ} \int_{- 1}^{t} (t - τ)^{- u} K (t, τ) u (τ) d τ

= {(\frac{T}{2})}^{1 - μ} \int_{- 1}^{1} {(\frac{t + 1}{2})}^{1 - μ} (1 - θ)^{- μ} K (t, τ (t, θ)) u (τ (t, θ)) d θ .

Using ( $N + 1$ )-point Gauss-Jacobi quadrature formula with weight $ω_{- μ, - μ}$ to approximate Eqs. (6)-(8) yields:

9

M u (t) \approx M_{N} u (t) : = \frac{T}{2} \sum_{j = 0}^{N} (\frac{t + 1}{2}) a (τ (t, θ_{j})) u (τ (t, θ_{j})) ω_{μ, μ} (θ_{j}) ω_{j},

10

\hat{M} u (t) \approx {\hat{M}}_{N} u (t) : = \frac{T}{2} \sum_{j = 0}^{N} (\frac{t + 1}{2}) u (τ (t, θ_{j})) ω_{μ, μ} (θ_{j}) ω_{j},

11

\tilde{M} u (t) \approx {\tilde{M}}_{N} u (t) : = {(\frac{T}{2})}^{1 - μ} \sum_{j = 0}^{N} {(\frac{t + 1}{2})}^{1 - μ} K (t, τ (t, θ_{j})) u (τ (t, θ_{j})) ω_{0, μ} (θ_{j}) ω_{j},

where ${θ_{j}}_{j = 0}^{N}$ are the ( $N +$ 1)-degree Jacobi-Gauss points associated with $ω_{- μ, - μ}$ , and ${ω_{j}}_{j = 0}^{N}$ are the corresponding Jacobi weights. On the other hand, instead of the continuous inner product, the discrete inner product will be implemented by the following equality:

12

(u, v)_{N} = \sum_{j = 0}^{N} u (θ_{j}) v (θ_{j}) ω_{j},

as a result $(u, v)_{ω_{- μ, - μ}} = (u, v)_{N}$ , if $u v \in P_{2 N} (Λ)$ .

By the definition of $I_{N}^{- μ, - μ}$ , we have:

13

(u, v)_{N} = (I_{N}^{- μ, - μ} u, v)_{N} .

The Jacobi pseudo-spectral Galerkin method is to find:

u_{N} (t) = \sum_{j = 0}^{N} {\tilde{u}}_{j} J_{j}^{- μ, - μ} (t), w_{N} (t) = \sum_{j = 0}^{N} {\tilde{w}}_{j} J_{j}^{- μ, - μ} (t) \in P_{N} (Λ),

such that:

14

\{\begin{array}{l} (u_{N}, v_{1})_{N} = (y_{0} + M_{N} u_{N} + {\hat{M}}_{N} w_{N}, v_{1})_{N}, \\ (w_{N}, v_{2})_{N} = (g (t) + {\tilde{M}}_{N} u_{N}, v_{2})_{N}, \end{array}

\forall (v_{1}, v_{2}) \in P_{N} (Λ) \times P_{N} (Λ),

where ${\{{\tilde{u}}_{j}\}}_{j = 0}^{N}$ and ${\{\tilde{w_{j}}\}}_{j = 0}^{N}$ are determined by:

15

\{\begin{array}{l} (\begin{matrix} \sum_{j = 0}^{N} \{{(J_{j}^{- μ, - μ}, J_{i}^{- μ, - μ})}_{N} - {(M_{N} J_{j}^{- μ, - μ}, J_{i}^{- μ, - μ})}_{N}\} {\tilde{u}}_{j} \\ - \sum_{j = 0}^{N} {({\hat{M}}_{N} J_{j}^{- μ, - μ}, J_{i}^{- μ, - μ})}_{N} {\tilde{w}}_{j} = {(y_{0}, J_{i}^{- μ, - μ})}_{N} \end{matrix}), \\ - \sum_{j = 0}^{N} {({\tilde{M}}_{N} J_{j}^{- μ, - μ}, J_{i}^{- μ, - μ})}_{N} {\tilde{u}}_{j} + \sum_{j = 0}^{N} {(J_{j}^{- μ, - μ}, J_{i}^{- μ, - μ})}_{N} {\tilde{w}}_{j} = {(g (t), J_{i}^{- μ, - μ})}_{N} . \end{array}

Denoting $\tilde{X} = {[{\tilde{u}}_{0}, {\tilde{u}}_{1}, . . ., {\tilde{u}}_{N}, {\tilde{w}}_{0}, {\tilde{w}}_{1}, . . ., {\tilde{w}}_{N}]}^{T}$ , Eq. (14) yields a equation of the matrix form:

16

A \tilde{X} = g_{N},

where:

A (i, j) = \{\begin{array}{l} {(J_{j}^{- μ, - μ}, J_{i}^{- μ, - μ})}_{N} - {(M_{N} J_{j}^{- μ, - μ}, J_{i}^{- μ, - μ})}_{N}, 0 \leq i \leq N, 0 \leq j \leq N, \\ - {({\tilde{M}}_{N} J_{j}^{- μ, - μ}, J_{i - N - 1}^{- μ, - μ})}_{N}, N + 1 \leq i \leq 2 N + 1, 0 \leq j \leq N, \\ - {({\tilde{M}}_{N} J_{j - N - 1}^{- μ, - μ}, J_{i}^{- μ, - μ})}_{N}, 0 \leq i \leq N, N + 1 \leq j \leq 2 N + 1, \\ {(J_{j - N - 1}^{- μ, - μ}, J_{i - N - 1}^{- μ, - μ})}_{N}, N + 1 \leq i \leq 2 N + 1, N + 1 \leq j \leq 2 N + 1, \end{array}

g_{N} (i) = \{\begin{array}{l} {(y_{0}, J_{i}^{- μ, - μ})}_{N}, 0 \leq i \leq N, \\ {(g (t), J_{i - N - 1}^{- μ, - μ})}_{N}, N + 1 \leq i \leq 2 N + 1 . \end{array}

3. Some useful lemmas

We first introduce some Hilbert spaces. For simplicity, denote $\partial_{t} v (t) = (\partial / \partial_{t}) v (t)$ , etc. For a nonnegative integer $m$ , define:

H_{ω_{α, β}}^{m} (- 1,1) : = \{v : \partial_{t}^{k} v (t) \in L_{ω_{α, β}}^{2} (- 1,1), 0 \leq k \leq m\},

with the semi-norm and the norm as:

{|v|}_{L_{ω_{α, β}}^{2}} = {‖\partial_{t}^{m} v (t)‖}_{L_{ω_{α, β}}^{2}}, {‖v‖}_{m} = {(\sum_{k = 0}^{m} {‖\partial_{t}^{k} v (t)‖}_{L_{ω_{α, β}}^{2}}^{2})}^{\frac{1}{2}},

respectively. It is convenient sometime to introduce the semi-norms:

{|v|}_{H_{ω_{α, β}}^{m, N}} = {(\sum_{k = \min (m, N + 1)}^{m} {|\partial_{t}^{k} v (t)|}_{L_{ω_{α, β}}^{2} (Λ)}^{2})}^{\frac{1}{2}} .

For bounding some approximation error of Jacobi polynomials, we need the following nonuniformly-weighted Sobolev spaces:

H_{ω_{α, β}}^{m} (- 1,1) : = \{v : \partial_{t}^{k} v (t) \in L_{ω_{α + k, β + k}}^{2} (- 1,1), 0 \leq k \leq m\},

equipped with the inner product and the norm as:

(u, v)_{m, *} = \sum_{k = 0}^{m} (\partial_{t}^{k} u, \partial_{t}^{k} v)_{ω_{α + k, β + k}}, {‖v‖}_{_{m, *}} = \sqrt{(v, v)_{m, *}} .

Next, we define the orthogonal projection $P_{N} : L^{2} (Λ) \to P_{N} (Λ)$ as:

(u - P_{N} u, v) = 0, \forall v \in P_{N} (Λ),

where $P_{N}$ possesses the following approximation properties ((5.4.11), (5.4.12) and (5.4.24) on p. 283-287 in Ref. ([11]):

17

{‖u - P_{N} u‖}_{L^{2} (Λ)} \leq c N^{- m} {‖u‖}_{H^{m} (Λ)},

and:

18

{‖u - P_{N} u‖}_{L^{\infty}} \leq c N^{\frac{3}{4} - m} {‖u‖}_{m, \infty} .

We have the following optimal error estimate for the interpolation polynomials based on the Jacobi Gauss points (c.f. [7]).

Lemma 3.1 For any function $v$ satisfying $v \in H_{ω_{α, β}, *}^{m} (- 1,1)$ , we have:

19

{‖v - I_{N}^{α, β} v‖}_{L_{ω_{α, β}}^{2} (Λ)} \leq c N^{- m} {‖\partial_{t}^{m} v‖}_{L_{ω_{α + m, β + m}}^{2}},

for the Jacobi Gauss points and Jacobi Gauss-Radau points.

Lemma 3.2 If $v \in H_{ω_{α, β}, *}^{m} (- 1,1)$ , for some $m \geq 1$ and $ϕ \in P_{N} (Λ)$ , then for the Jacobi Gauss and Jacobi Gauss-Radau integration we have (cf. [7]):

20

|(v, ϕ)_{ω_{α, β}} - (v, ϕ)_{N}| \leq {‖v - I_{N}^{α, β} v‖}_{L_{ω_{α, β}}^{2}} {‖ϕ‖}_{L_{ω_{α, β}}^{2}} \leq c N^{- m} {‖\partial_{t}^{m} v‖}_{L_{ω_{α + m, β + m}}^{2}} {‖ϕ‖}_{L_{ω_{α, β}}^{2}} .

We have the following result on the Lebesgue constant for the Lagrange interpolation poly-nomials associated with the zeros of the Jacobi polynomials; (cf. [7]).

Lemma 3.3 Let ${\{F_{j} (t)\}}_{j = 0}^{N}$ be the $N$ -th Lagrange interpolation polynomials associated with the Gauss, or Gauss-Radau, or Gauss-Lobatto points of the Jacobi polynomials. Then:

21

{‖I_{N}^{α, β}‖}_{L^{\infty}} : = \underset{t \in [- 1,1]}{m a x} \sum_{j = 0}^{N} |F_{j} (t)| = \{\begin{array}{l} c l o g N, - 1 \leq α, β \leq - \frac{1}{2}, \\ c N^{γ + \frac{1}{2}}, γ = m a x (α, β), otherwise . \end{array}

We now introduce some notation. For $r \geq 0$ and $k \in [0,1]$ , $C^{r, k} ([- 1,1])$ will denote the space of functions whose $r$ -th derivatives are Holder continuous with exponent $k$ , endowed with the usual norm ${‖.‖}_{r, k}$ . When $k =$ 0, $C^{r, 0} ([- 1,1])$ denotes the space of functions with $r$ continuous derivatives on [0, $T$ ], also denoted by $C^{r} ([- 1,1])$ , and with norm ${‖.‖}_{r}$ .

We will make use of a result of Ragozin ([12-13]), which states that, for each nonnegative Integer $r$ and $k \in [0,1],$ there exists a constant $C^{r, k} >$ 0 such that for any function $v \in C^{r, k} ([- 1,1])$ there exists a polynomial function $τ_{N} v \in P_{N}$ such that:

22

{‖v - τ_{N} v‖}_{L^{\infty}} \leq C_{r, k} N^{- (r + k)} {‖v‖}_{r, k},

where ${‖.‖}_{\infty}$ is the norm of the space $L^{\infty} ([- 1,1]),$ and when the function $v \in C ([- 1,1]) .$ Actually, $τ_{N}$ is a linear operator from $C^{r, k} ([- 1,1])$ to $P_{N}$ .

We will need the fact that $\tilde{M}$ , which be defined by Eq. (11), is compact as an operator from $C ([0, T])$ to $C^{r, k} ([- 1,1])$ for any $0 < k < 1 - μ$ [14].

Lemma 3.4 Let $0 < k < 1 - μ$ , then, for any function $v \in C ([- 1,1])$ , there exists a positive constant $C$ such that:

\frac{|\tilde{M} v (t^{'}) - \tilde{M} v (t^{''})|}{{|t^{'} - t^{''}|}^{k}} \leq c \underset{- 1 \leq t \leq 1}{m a x} |v (t)|,

under the assumption that $0 < k < 1 - μ$ for any $t^{'}$ , $t^{''} \in [- 1,1]$ and $t^{'} \neq t^{''}$ . This implies that:

23

{‖\tilde{M} v‖}_{0, k} \leq C {‖v (t)‖}_{L^{\infty}}, 0 < k < 1 - μ .

Clearly, $M$ and $\hat{M}$ also satisfy Eq. (24). In our analysis, we shall apply the generalization of Gronwalls lemma. We call such a function $v (t)$ locally integrable on the interval [0, $T$ ] if for each $t \in [0, T]$ , its Lebesgue integral $\int_{0}^{t} v (s) d s$ is finite. The following result can be found in [15].

Lemma 3.5 Suppose that:

v (t) \leq w_{*} (t) + w (t) \int_{0}^{t} ϕ (t, s) v (s) d s, t \in [0, T],

where $ϕ w$ , $ϕ w_{*}$ and $ϕ v$ are locally integrable on the interval [0, $T$ ]. Here, all the functions are assumed to be nonnegative. Then:

v (t) \leq w_{*} (t) + w (t) (e x p \int_{0}^{t} ϕ (t, s) w (s) d s) \int_{0}^{t} ϕ (t, s) w_{*} (s) d s, t \in [0, T] .

Lemma 3.6 Assume that $v$ is a nonnegative, locally integrable function defined on [0, $T$ ] and satisfying:

v (t) \leq w_{*} (t) + K_{0} \int_{0}^{t} (t - s)^{- μ} v (s) d s, t \in [0, T],

where $K_{0}$ is a positive constant and $w_{*} (t)$ is a nonnegative and continuous function defined on [0, $T$ ]. Then, there exists a constant $C$ such that:

v (t) \leq w_{*} (t) + C \int_{0}^{t} (t - s)^{- μ} w_{*} (s) d s, t \in [0, T] .

Proof. We note that when $0 < μ < 1$ , the integral $\int_{0}^{t} (t - s)^{- μ} d s$ is finite. From Lemma 3.5, we obtain the desired result directly.

Lemma 3.7 Assume that $v$ is a nonnegative, locally integrable function defined on [−1, 1] and satisfying:

v (t) \leq w_{*} (t) + K_{0} \int_{- 1}^{t} (t - s)^{- μ} v (s) d s,

where $K_{0}$ is a positive constant and $w_{*} (t)$ is a nonnegative and continuous function defined on [−1, 1]. Then, there exists a constant $C$ such that:

v (t) \leq w_{*} (t) + C \int_{- 1}^{t} (t - s)^{- μ} w_{*} (s) d s .

Proof. Let $t = 2 / T (x - 1)$ , $s = 2 / T (τ - 1)$ , we obtain that:

v (x) \leq w_{*} (x) + {\tilde{K}}_{0} {(\frac{2}{T})}^{1 - μ} \int_{0}^{x} (x - τ)^{- μ} v (τ) d τ, x \in [0, T] .

Using Lemma 3.6 leads to:

v (x) \leq w_{*} (x) + \tilde{C} \int_{0}^{x} (x - τ)^{- μ} w_{*} (τ) d τ, x \in [0, T] .

By the linear transformation $x = 2 / T (t + 1)$ , $τ = 2 / T (s + 1)$ , desired result follows. Obviously, when $μ =$ 0, the lemma 3.7 also holds.

To prove the error estimate in the weighted $L^{2}$ -norm, we need the generalized Hardys inequality with weights (see, e.g., [16, 17]).

Lemma 3.8 For all measurable function $f \geq$ 0, the following generalized Hardys inequality:

{(\int_{a}^{b} {|(k f) (x)|}^{q} ω_{1} (x) d x)}^{\frac{1}{q}} \leq c {(\int_{a}^{b} {|f (x)|}^{p} ω_{2} (x) d x)}^{\frac{1}{p}},

holds if and only if:

\underset{a < x < b}{S u p} {(\int_{x}^{b} ω_{1} (t) d t)}^{\frac{1}{q}} {(\int_{a}^{x} ω_{2}^{^{1 - q^{'}}} (t) d t)}^{\frac{1}{q^{'}}} < \infty, q^{'} = \frac{p}{p - 1},

for the case $1 < p \leq q < \infty$ . Here, $k$ is an operator of the form:

(k f) (x) = \int_{a}^{x} ρ (x, t) f (t) d t,

with $ρ (x, t)$ a given kernel, $ω_{1}$ , $ω_{2}$ weight functions, and $- \infty \leq a ≺ v \leq \infty$ .

We will need the following estimate for the Lagrange interpolation associated with the Jacobi Gaussian collocation points.

Lemma 3.9 For every bounded function $v$ , there exists a constant $C$ independent of $v$ such that:

{‖I_{N}^{α, β} v (t)‖}_{L^{\infty}} = {‖\sum_{j = 0}^{N} |v (t_{j}) F_{j} (t)|‖}_{L^{\infty}} \leq \{\begin{array}{l} c l o g N {‖v‖}_{L^{\infty}}, - 1 < α, β \leq - \frac{1}{2}, \\ c N^{γ + \frac{1}{2}} {‖v‖}_{L^{\infty}}, γ = m a x (α, β), otherwise, \end{array}

where $F_{j} (t)$ is the Lagrange interpolation basis function associated with the Jacobi collocation points ${\{t_{j}\}}_{j = 0}^{N}$ .

Proof. It is obvious that:

‖I_{N}^{α, β} v (t)‖ = {‖\sum_{j = 0}^{N} |v (t_{j}) F_{j} (t)|‖}_{L^{\infty}} \leq \underset{t \in [- 1,1]}{m a x} \sum_{j = 0}^{N} |v (t_{j}) F_{j} (t)|

\leq (\underset{t \in [- 1,1]}{m a x} \sum_{j = 0}^{N} |F_{j} (t)|) {‖v‖}_{L^{\infty}} .

By the Lemma 3.3, we obtain the desired result.

Lemma 3.10 For every bounded function $v$ , there exists a constant $C$ independent of $v$ such that:

{‖I_{N}^{α, β} v (t)‖}_{L_{ω_{α, β}}^{2}} \leq c {‖v‖}_{L^{\infty}},

where $F_{j} (t)$ is the Lagrange interpolation basis function associated with the Jacobi collocation points ${\{t_{j}\}}_{j = 0}^{N}$ .

Proof. It is obvious that:

{‖I_{N}^{α, β} v (t)‖}_{_{L_{ω_{α, β}}^{2}}}^{2} = \int_{- 1}^{1} {(I_{N}^{α, β} v)}^{2} ω_{α, β} d t = \sum_{j = 0}^{N} v^{2} (t_{j}) ω_{j} \leq {‖v‖}_{L^{\infty}}^{2} \sum_{j = 0}^{N} ω_{j} = γ_{0} {‖v‖}_{L^{\infty}},

where $γ_{0} = c_{0} {(J_{0}^{α, β}, J_{0}^{α, β})}_{ω_{α, β}}$ . As a consequence:

\underset{N}{s u p} {‖I_{N}^{α, β} v (t)‖}_{_{L_{ω_{α, β}}^{2}}}^{2} \leq C {‖v‖}_{L^{\infty}},

with $C = \sqrt{γ_{0}} .$

4. Convergence for Jacobi pseudo-spectral-Galerkin method

As $I_{N}^{- μ, - μ}$ is the interpolation operator which is based on the ( $N +$ 1)-degree Jacobi-Gauss points with weight $ω_{- μ, - μ}$ , in terms of Eqs. (13) and (14), the pseudo-spectral Galerkin solution $u_{N}$ , $w_{N}$ satisfies:

24

\{\begin{array}{l} (u_{N}, v_{1})_{ω_{- μ, - μ}} - {(I_{N}^{- μ, - μ} (M_{N} u_{N} + {\hat{M}}_{N} w_{N}), v_{1})}_{ω_{- μ, - μ}} = {(I_{N}^{- μ, - μ} y_{0}, v_{1})}_{ω_{- μ, - μ}}, \\ (w_{N}, v_{2})_{ω_{- μ, - μ}} - {(I_{N}^{- μ, - μ} {\tilde{M}}_{N} u_{N}, v_{2})}_{ω_{- μ, - μ}} = {(I_{N}^{- μ, - μ} g (t), v_{2})}_{ω_{- μ, - μ}}, \\ \forall (v_{1}, v_{2}) \in P_{N} (Λ) \times P_{N} (Λ), \end{array}

where:

M_{N} u_{N} = M u_{N} - (M u_{N} - M_{N} u_{N}) = M u_{N} - Q (t),

with:

25

Q (t) = M u_{N} - M_{N} u_{N} = \frac{T}{2} \int_{- 1}^{1} (\frac{t + 1}{2}) a (τ (t, θ)) u_{N} (τ (t, θ)) d θ

- \frac{T}{2} \sum_{j = 0}^{N} (\frac{t + 1}{2}) a (τ (t, θ_{j})) u_{N} (τ (t, θ_{j})) ω_{μ, μ} (θ_{j}) ω_{j}

= \frac{T}{2} {((\frac{t + 1}{2}) a (τ (t, \cdot)) ω_{μ, μ}, u_{N} (τ (t, \cdot)))}_{ω_{- μ, - μ}}

- \frac{T}{2} {((\frac{t + 1}{2}) a (τ (t, \cdot)) ω_{μ, μ}, u_{N} (τ (t, \cdot)))}_{N},

in which $(\cdot, \cdot)_{ω_{- μ, - μ}}$ represents the continuous inner product with respect to $θ$ , and $(\cdot, \cdot)_{N}$ is the corresponding discrete inner product defined by the Gauss-Jacobi quadrature formula. Similar to Eq. (25), we have that:

{\hat{M}}_{N} w_{N} = \hat{M} w_{N} - (\hat{M} w_{N} - {\hat{M}}_{N} w_{N}) = \hat{M} w_{N} - \hat{Q} (t),

with:

26

\hat{Q} (t) = \hat{M} w_{N} - {\hat{M}}_{N} w_{N} = \frac{T}{2} \int_{- 1}^{1} (\frac{t + 1}{2}) w_{N} (τ (t, θ)) d θ

- \frac{T}{2} \sum_{j = 0}^{N} (\frac{t + 1}{2}) w_{N} (τ (t, θ_{j})) ω_{μ, μ} (θ_{j}) ω_{j}

= \frac{T}{2} {((\frac{t + 1}{2}) ω_{μ, μ}, w_{N} (τ (t, \cdot)))}_{ω_{- μ, - μ}}

- \frac{T}{2} {((\frac{t + 1}{2}) ω_{μ, μ}, w_{N} (τ (t, \cdot)))}_{N},

and:

{\tilde{M}}_{N} u_{N} = \tilde{M} u_{N} - (\tilde{M} u_{N} - {\tilde{M}}_{N} u_{N}) = \tilde{M} u_{N} - \tilde{Q} (t),

with:

27

\tilde{Q} (t) = \tilde{M} u_{N} - {\tilde{M}}_{N} u_{N} = {(\frac{T}{2})}^{1 - μ} \int_{- 1}^{1} {(\frac{t + 1}{2})}^{1 - μ} (1 - θ)^{- μ} K (t, τ (t, θ)) u_{N} (τ (t, θ)) d θ

- {(\frac{T}{2})}^{1 - μ} \sum_{j = 0}^{N} {(\frac{t + 1}{2})}^{1 - μ} K (t, τ (t, θ_{j})) ω_{0, μ} u_{N} (τ (t, θ_{j})) ω_{j}

= {(\frac{T}{2})}^{1 - μ} \{{({(\frac{t + 1}{2})}^{1 - μ} K (t, τ (t, \cdot)) ω_{0, μ}, u_{N} (τ (t, \cdot)))}_{ω_{- μ, - μ}}

- {({(\frac{t + 1}{2})}^{1 - μ} K (t, τ (t, \cdot)) ω_{0, μ}, u_{N} (τ (t, \cdot)))}_{N}\} .

The combination of Eqs. (24)-(27) yields:

\{\begin{array}{l} (\begin{array}{l} {(u_{N} + I_{N}^{- μ, - μ} Q (t) - I_{N}^{- μ, - μ} M u_{N} + I_{N}^{- μ, - μ} \hat{Q} (t) - I_{N}^{- μ, - μ} \hat{M} w_{N}, v_{1})}_{ω_{- μ, - μ}} \\ = {(I_{N}^{- μ, - μ} y_{0}, v_{1})}_{ω_{- μ, - μ},} \end{array}), \\ (w_{N}, v_{2})_{ω_{- μ, - μ}} + {(I_{N}^{- μ, - μ} \tilde{Q} (t) - I_{N}^{- μ, - μ} \tilde{M} u_{N}, v_{2})}_{ω_{- μ, - μ}} = {(I_{N}^{- μ, - μ} g (t), v_{2})}_{ω_{- μ, - μ}}, \end{array}

which gives rise to:

28

\{\begin{array}{l} u_{N} + I_{N}^{- μ, - μ} Q (t) - I_{N}^{- μ, - μ} M u_{N} + I_{N}^{- μ, - μ} \hat{Q} (t) - I_{N}^{- μ, - μ} \hat{M} w_{N} = I_{N}^{- μ, - μ} y_{0}, \\ w_{N} + I_{N}^{- μ, - μ} \tilde{Q} (t) - I_{N}^{- μ, - μ} \tilde{M} u_{N} = I_{N}^{- μ, - μ} g (t) . \end{array}

By the discussion above, Eqs. (14), (24) and (28) are equivalent.

We first consider an auxiliary problem. We want to find ${\hat{u}}_{N}$ , ${\hat{w}}_{N} \in P_{N} (Λ)$ such that:

29

\{\begin{array}{l} ({\hat{u}}_{N}, v_{1})_{N} - {(Μ {\hat{u}}_{N}, v_{1})}_{N} - {(\hat{M} {\hat{w}}_{N}, v_{1})}_{N} = (y_{0}, v_{1})_{N}, \\ ({\hat{w}}_{N}, v_{2})_{N} - {(\tilde{M} {\hat{u}}_{N}, v_{2})}_{N} = (g (t), v_{2})_{N}, \end{array}

\forall (v_{1}, v_{2}) \in P_{N} (Λ) \times P_{N} (Λ),

where $M$ , $\tilde{M}$ and $\hat{M}$ are the integral operators defined in Section 2, and $(., .)_{N}$ is still the discrete inner product based on the ( $N +$ 1)-degree Jacobi-Gauss points. In terms of the definition of $I_{N}^{- μ, - μ}$ , Eq. (29) can be written as:

30

\{\begin{array}{l} ({\hat{u}}_{N}, v_{1})_{N} - {(I_{N}^{- μ, - μ} M {\hat{u}}_{N}, v_{1})}_{N} - {(I_{N}^{- μ, - μ} \hat{M} {\hat{w}}_{N}, v_{1})}_{N} = {(I_{N}^{- μ, - μ} y_{0}, v_{1})}_{N}, \\ ({\hat{w}}_{N}, v_{2})_{N} - {(I_{N}^{- μ, - μ} \tilde{M} {\hat{u}}_{N}, v_{2})}_{N} = {(I_{N}^{- μ, - μ} g (t), v_{2})}_{N}, \end{array}

which is equivalent to:

31

\{\begin{array}{l} {\hat{u}}_{N} - I_{N}^{- μ, - μ} M {\hat{u}}_{N} - I_{N}^{- μ, - μ} \hat{M} {\hat{w}}_{N} = I_{N}^{- μ, - μ} y_{0}, \\ {\hat{w}}_{N} - I_{N}^{- μ, - μ} \tilde{M} {\hat{u}}_{N} = I_{N}^{- μ, - μ} g (t) . \end{array}

When $y_{0} = g = 0$ , Eq. (31) can be written as:

\{\begin{array}{l} {\hat{u}}_{N} - I_{N}^{- μ, - μ} M {\hat{u}}_{N} - I_{N}^{- μ, - μ} \hat{M} {\hat{w}}_{N} = 0, \\ {\hat{w}}_{N} - I_{N}^{- μ, - μ} \tilde{M} {\hat{u}}_{N} = 0 . \end{array}

In terms of the fact that:

\{\begin{array}{l} {\hat{u}}_{N} - I_{N}^{- μ, - μ} M {\hat{u}}_{N} - I_{N}^{- μ, - μ} \hat{M} {\hat{w}}_{N} = (\begin{matrix} {\hat{u}}_{N} - M {\hat{u}}_{N} + (M {\hat{u}}_{N} - I_{N}^{- μ, - μ} M {\hat{u}}_{N}) - \hat{M} {\hat{w}}_{N} \\ + (\hat{M} {\hat{w}}_{N} - I_{N}^{- μ, - μ} \hat{M} {\hat{w}}_{N}) \end{matrix}), \\ {\hat{w}}_{N} - I_{N}^{- μ, - μ} \tilde{M} {\hat{u}}_{N} = {\hat{w}}_{N} - \tilde{M} {\hat{u}}_{N} + (\tilde{M} {\hat{u}}_{N} - I_{N}^{- μ, - μ} \tilde{M} {\hat{u}}_{N}) . \end{array}

Suppose that:

m a x \{{(\frac{T}{2})}^{1 - μ} | K (t, s |, \frac{T}{2} | a (t) |, \frac{T}{2}\} \leq L .

It is clear that from Eq. (6)-(8):

\{\begin{array}{l} {\hat{u}}_{N} = \frac{T}{2} \int_{- 1}^{t} (a (s) {\hat{u}}_{N} (s) + {\hat{w}}_{N} (s)) d s + I_{N}^{- μ, - μ} M {\hat{u}}_{N} - M {\hat{u}}_{N} + I_{N}^{- μ, - μ} \hat{M} {\hat{w}}_{N} - \hat{M} {\hat{w}}_{N}, \\ {\hat{w}}_{N} = {(\frac{T}{2})}^{1 - μ} \int_{- 1}^{t} (t - s)^{- μ} K (t, s) {\hat{u}}_{N} (s) d s + I_{N}^{- μ, - μ} \tilde{M} {\hat{u}}_{N} - \tilde{M} {\hat{u}}_{N}, \end{array}

which yields:

(|{\hat{u}}_{N}| + |{\hat{w}}_{N}|) \leq c \int_{- 1}^{t} ((t - s)^{- μ} + 1) (| {\hat{u}}_{N} (s) | + | {\hat{w}}_{N} (s) |) d s + | I_{1} | + | I_{2} | + | I_{3} |,

where $I_{1} = I_{N}^{- μ, - μ} M {\hat{u}}_{N} - M {\hat{u}}_{N},$ $I_{2} = I_{N}^{- μ, - μ} \hat{M} {\hat{w}}_{N} - \hat{M} {\hat{w}}_{N},$ $I_{3} = I_{N}^{- μ, - μ} \tilde{M} {\hat{u}}_{N} - \tilde{M} {\hat{u}}_{N} .$ Using Lemma 3.7 leads to:

\begin{matrix} (| {\hat{u}}_{N} | + | {\hat{w}}_{N} |) \leq c \int_{- 1}^{t} ((t - s)^{- μ} + 1) (| I_{1} | + | I_{2} | + | I_{3} |) d s + | I_{1} | + | I_{2} | + | I_{3} | \end{matrix}

\leq c ({‖I_{1}‖}_{L^{\infty}} + {‖I_{2}‖}_{L^{\infty}} + {‖I_{3}‖}_{L^{\infty}}),

namely:

32

‖| {\hat{u}}_{N} | + | {\hat{w}}_{N} | ‖_{L^{\infty}} \leq c ({‖I_{1}‖}_{L^{\infty}} + {‖I_{2}‖}_{L^{\infty}} + {‖I_{3}‖}_{L^{\infty}}) .

We now estimate ${‖I_{1}‖}_{L^{\infty}},$ ${‖I_{2}‖}_{L^{\infty}}$ and ${‖I_{3}‖}_{L^{\infty}} .$ By virtue of Eqs. (22), (23) and Lemma 3.9, we obtain that:

\begin{matrix} {‖I_{N}^{- μ, - μ} \tilde{M} {\hat{u}}_{N} - \hat{M} {\hat{u}}_{N}‖}_{L^{\infty}} = {‖(I - I_{N}^{- μ, - μ}) \tilde{M} {\hat{u}}_{N}‖}_{L^{\infty}} = {‖(I - I_{N}^{- μ, - μ}) (\tilde{M} {\hat{u}}_{N} - τ_{N} \tilde{M} {\hat{u}}_{N})‖}_{L^{\infty}} \end{matrix}

\leq (1 + {‖I_{N}^{- μ, - μ}‖}_{L^{\infty}}) {‖\tilde{M} {\hat{u}}_{N} - τ_{N} \tilde{M} {\hat{u}}_{N}‖}_{L^{\infty}}

\leq \{\begin{array}{l} c l o g N {‖\tilde{M} {\hat{u}}_{N} - τ_{N} \tilde{M} {\hat{u}}_{N}‖}_{L^{\infty}} \leq c l o g N N^{- κ} {‖{\hat{u}}_{N}‖}_{L^{\infty}}, - 1 < - μ \leq - \frac{1}{2}, \\ c N^{\frac{1}{2} - μ} {‖\tilde{M} {\hat{u}}_{N} - τ_{N} \tilde{M} {\hat{u}}_{N}‖}_{L^{\infty}} \leq c N^{\frac{1}{2} - κ - μ} {‖{\hat{u}}_{N}‖}_{L^{\infty}}, - \frac{1}{2} < - μ < 0 . \end{array}

Similarly:

{‖I_{N}^{- μ, - μ} \hat{M} {\hat{w}}_{N} - \hat{M} {\hat{w}}_{N}‖}_{L^{\infty}} \leq \{\begin{array}{l} c l o g N N^{- κ} {‖{\hat{w}}_{N}‖}_{L^{\infty}}, - 1 < - μ \leq - \frac{1}{2}, \\ c N^{\frac{1}{2} - κ - μ} {‖{\hat{w}}_{N}‖}_{L^{\infty}}, - \frac{1}{2} < - μ < 0, \end{array}

and:

{‖I_{N}^{- μ, - μ} M {\hat{u}}_{N} - M {\hat{u}}_{N}‖}_{L^{\infty}} \leq \{\begin{array}{l} c l o g N N^{- κ} {‖{\hat{u}}_{N}‖}_{L^{\infty}}, - 1 < - μ \leq \frac{1}{2}, \\ c N^{\frac{1}{2} - κ - μ} {‖{\hat{u}}_{N}‖}_{L^{\infty}}, - 1 < - μ \leq < 0 . \end{array}

These, together with Eq. (32), give:

{‖| {\hat{u}}_{N} | + | {\hat{w}}_{N} |‖}_{L^{\infty}} \leq \{\begin{array}{l} c l o g N N^{- κ} {‖| {\hat{u}}_{N} | + | {\hat{w}}_{N} |‖}_{L^{\infty}}, - 1 < - μ \leq - \frac{1}{2}, \\ c N^{\frac{1}{2} - κ - μ} {‖| {\hat{u}}_{N} | + | {\hat{w}}_{N} |‖}_{L^{\infty}}, - \frac{1}{2} < - μ < 0, \end{array}

which implies, taking $μ$ , $κ \in (0,1 - μ)$ such that $μ + κ > 1 / 2,$ when $N$ is large enough, ${\hat{u}}_{N} = {\hat{w}}_{N} =$ 0. Hence, the ${\hat{u}}_{N}$ and ${\hat{w}}_{N}$ are existent and unique as $P_{N} (Λ)$ is finite-dimensional.

Lemma 4.1. Suppose that $u \in H_{ω_{- μ ， - μ}}^{m} (Λ)$ and:

m a x \{{(\frac{T}{2})}^{1 - μ} |K (t, s)|, \frac{T}{2} |a (t)|, \frac{T}{2}\} \leq L,

then we have:

33

{‖| u - {\hat{u}}_{N} | + | w - {\hat{w}}_{N} |‖}_{L^{\infty}} \leq \{\begin{array}{l} c l o g N N^{\frac{3}{4} - m} ({‖u‖}_{m, \infty} + {‖w‖}_{m, \infty}), & - 1 < - μ \leq \frac{1}{2}, \\ c N^{\frac{5}{4} - m - μ} ({‖u‖}_{m, \infty} + {‖w‖}_{m, \infty}), & - \frac{1}{2} < - μ < 0, \end{array}

34

{‖| u - {\hat{u}}_{N} | + | w - {\hat{w}}_{N} |‖}_{L_{ω_{- μ, - μ}}^{2}} \leq \{\begin{array}{l} (\begin{matrix} c N^{- m} ({‖\partial_{t}^{m} u‖}_{L_{ω_{m - μ, m - μ}}^{2}} + {‖\partial_{t}^{m} w‖}_{L_{ω_{m - μ, m - μ}}^{2}}) \\ + c l o g N N^{\frac{3}{4} - m} ({‖u‖}_{m, \infty} + {‖w‖}_{m, \infty}), - 1 < - μ \leq \frac{1}{2} \end{matrix}), \\ (\begin{matrix} c N^{- m} ({‖\partial_{t}^{m} u‖}_{L_{ω_{m - μ, m - μ}}^{2}} + {‖\partial_{t}^{m} w‖}_{L_{ω_{m - μ, m - μ}}^{2}}) \\ + c N^{\frac{5}{4} - m - μ} ({‖u‖}_{m, \infty} + {‖w‖}_{m, \infty}), - \frac{1}{2} < - μ < 0 \end{matrix}) . \end{array}

Proof. Subtracting Eq. (31) from Eq. (3) yields:

35

\{\begin{array}{l} u (t) - {\hat{u}}_{N} + I_{N}^{- μ, - μ} M {\hat{u}}_{N} + I_{N}^{- μ, - μ} \hat{M} {\hat{w}}_{N} - M u - \hat{M} w (t) = y_{0} - I_{N}^{- μ, - μ} y_{0}, \\ w - {\hat{w}}_{N} + I_{N}^{- μ, - μ} \tilde{M} {\hat{u}}_{N} - \tilde{M} u = g (t) - I_{N}^{- μ, - μ} g (t) . \end{array}

Set $ε = u (t) - {\hat{u}}_{N}$ , $\hat{ε} = w (t) - {\hat{w}}_{N}$ . Direct computation shows that:

36

M u - I_{N}^{- μ, - μ} M {\hat{u}}_{N} + \hat{M} w - I_{N}^{- μ, - μ} \hat{M} {\hat{w}}_{N}

= M u - I_{N}^{- μ, - μ} M u + I_{N}^{- μ, - μ} M (u - {\hat{u}}_{N}) + \hat{M} w - I_{N}^{- μ, - μ} \hat{M} w + I_{N}^{- μ, - μ} \hat{M} (w - {\hat{w}}_{N})

= M u - I_{N}^{- μ, - μ} \hat{M} u + M (u - {\hat{u}}_{N}) - [M (u - {\hat{u}}_{N}) - I_{N}^{- μ, - μ} \hat{M} (u - {\hat{u}}_{N})]

+ \hat{M} w - I_{N}^{- μ, - μ} \hat{M} w + \hat{M} (w - {\hat{w}}_{N}) - [\hat{M} (w - {\hat{w}}_{N}) - I_{N}^{- μ, - μ} \hat{M} (w - {\hat{w}}_{N})]

= u - y_{0} - I_{N}^{- μ, - μ} (u - y_{0}) + M (u - {\hat{u}}_{N}) - [M (u - {\hat{u}}_{N}) - I_{N}^{- μ, - μ} \hat{M} (u - {\hat{u}}_{N})]

+ \hat{M} (w - {\hat{w}}_{N}) - [\hat{M} (w - {\hat{w}}_{N}) - I_{N}^{- μ, - μ} \hat{M} (w - {\hat{w}}_{N})]

= u - I_{N}^{- μ, - μ} u + M ε - [M ε - I_{N}^{- μ, - μ} M ε] + \hat{M} \hat{ε} - [\hat{M} \hat{ε} - I_{N}^{- μ, - μ} \hat{M} \hat{ε}],

and:

37

\tilde{M} u - I_{N}^{- μ, - μ} \tilde{M} {\hat{u}}_{N} = \tilde{M} u - I_{N}^{- μ, - μ} \tilde{M} u + I_{N}^{- μ, - μ} \tilde{M} (u - {\hat{u}}_{N})

= \tilde{M} u - I_{N}^{- μ, - μ} \tilde{M} u + \tilde{M} (u - {\hat{u}}_{N}) - [\tilde{M} (u - {\hat{u}}_{N}) - I_{N}^{- μ, - μ} \tilde{M} (u - {\hat{u}}_{N})]

= w - g (t) - I_{N}^{- μ, - μ} (w - g (t)) + \tilde{M} (u - {\hat{u}}_{N}) - [\tilde{M} (u - {\hat{u}}_{N}) - I_{N}^{- μ, - μ} \tilde{M} (u - {\hat{u}}_{N})]

= w - I_{N}^{- μ, - μ} w - g (t) + I_{N}^{- μ, - μ} g (t) + \tilde{M} ε - [\tilde{M} ε - I_{N}^{- μ, - μ} \tilde{M} ε] .

The insertion of Eqs. (36), (37) into Eq. (35) yields:

\{\begin{array}{l} ε = u - I_{N}^{- μ, - μ} u + M ε - [M ε - I_{N}^{- μ, - μ} M ε] + \hat{M} \hat{ε} - [\hat{M} \hat{ε} - I_{N}^{- μ, - μ} \hat{M} ε], \\ \hat{ε} = w - I_{N}^{- μ, - μ} w + \tilde{M} ε - [\tilde{M} ε - I_{N}^{- μ, - μ} \tilde{M} ε], \end{array}

which implies that:

38

| ε | + | \hat{ε} | \leq | J_{1} | + | J_{2} | + | J_{3} | + | J_{4} | + | J_{5} | + c \int \begin{array}{l} t \\ - 1 \end{array} ((t . s)^{- μ} + 1) (|ε (s)| + |\hat{ε} (s)|) d s,

where:

J_{1} = u - I_{N}^{- μ, - μ} u, J_{2} = M ε - I_{N}^{- μ, - μ} M ε, J_{3} = \hat{M} \hat{ε} - I_{N}^{- μ, - μ} \hat{M} \hat{ε},

J_{4} = w - I_{N}^{- μ, - μ} w, J_{5} = \tilde{M} ε - I_{N}^{- μ, - μ} \tilde{M} ε .

Using Lemma 3.7 gives:

39

|ε| + |\hat{ε}| \leq |J_{1}| + |J_{2}| + |J_{3}| + |J_{4}| + |J_{5}|

+ c \int \begin{array}{l} t \\ - 1 \end{array} ((t - s)^{- μ} + 1) (|J_{1}| + |J_{2}| + |J_{3}| + |J_{4}| + |J_{5}|) d s .

Then, it follows from Eq. (39) that:

40

\begin{array}{l} {‖| ε | + | \hat{ε} |‖}_{L^{\infty}} \leq c ({‖u - I_{N}^{- μ, - μ} u‖}_{L^{\infty}} + {‖M ε - I_{N}^{- μ, - μ} M ε‖}_{L^{\infty}} + {‖\hat{M} \hat{ε} - I_{N}^{- μ, - μ} \hat{M} \hat{ε}‖}_{L^{\infty}} \\ + {‖w - I_{N}^{- μ, - μ} w‖}_{L^{\infty}} + {‖\tilde{M} ε - I_{N}^{- μ, - μ} \tilde{M} ε‖}_{L^{\infty}}) . \end{array}

By using Eq. (18), Lemma 3.9, we obtain that:

41

{‖u - I_{N}^{- μ, - μ} u‖}_{L^{\infty}} = {‖(I - I_{N}^{- μ, - μ}) (u - P_{N} u)‖}_{L^{\infty}}

\begin{array}{l} \leq c (1 + {‖(I - I_{N}^{- μ, - μ})‖}_{\infty}) {‖u - P_{N} u‖}_{L^{\infty}} \leq \{\begin{array}{l} c l o g N N^{\frac{3}{4} - m} {‖u‖}_{m, \infty}, - 1 < - μ \leq - \frac{1}{2}, \\ c N^{\frac{5}{4} - m - μ} {‖u‖}_{m, \infty}, - \frac{1}{2} < - μ < 0, \end{array} \end{array}

and:

42

{‖w - I_{N}^{- μ, - μ} w‖}_{L^{\infty}} \leq \{\begin{array}{l} c l o g N N^{\frac{3}{4} - m} {‖w‖}_{m, \infty}, - 1 < - μ \leq - \frac{1}{2}, \\ c N^{\frac{5}{4} - m - μ} {‖w‖}_{m, \infty}, - \frac{1}{2} < - μ < 0 . \end{array}

We now estimate $J_{5}$ it is clear that $ε \in C [0, T] .$ Consequently, using Eqs. (22), (23) and Lemma 3.9 it follows that:

43

{‖J_{5}‖}_{L \infty} = {‖(I - I_{N}^{- μ, - μ}) (\tilde{M} ε - τ_{N} \tilde{M} ε)‖}_{L^{\infty}} \leq (1 + {‖I_{N}^{- μ, - μ}‖}_{L^{\infty}}) {‖\tilde{M} ε - τ_{N} \tilde{M} ε‖}_{L^{\infty}}

\leq c (1 + {‖I_{N}^{- μ, - μ}‖}_{L^{\infty}}) N^{- k} {‖\tilde{M} ε‖}_{0, k} \leq \{\begin{array}{l} c l o g N N^{- k} {‖| ε | + | \hat{ε} |‖}_{L^{\infty}}, - 1 < - μ \leq - \frac{1}{2}, \\ c N^{\frac{1}{2} - k - μ} {‖| ε | + | \hat{ε} |‖}_{L^{\infty}}, - \frac{1}{2} < - μ \leq 0, \end{array}

where $κ \in (0,1 - μ)$ and $τ_{N} M ε \in P_{_{N}} (Λ)$ . Eq. (43) also holds for ${‖J_{2}‖}_{L^{\infty}}$ and ${‖J_{3}‖}_{L^{\infty}}$ . Taking $μ$ , $κ \in (0,1 - μ)$ such that $κ + μ > 1 / 2$ , the estimate Eq. (33) follows from Eqs. (40)-(43), provider that $N$ is large enough.

Next we prove Eq. (34). Using the generalized Gronwall inequality (Lemma 3.8), we have from Eq. (38) that:

44

{‖|ε| + |\hat{ε}|‖}_{L_{ω_{- μ, - μ}}^{2}}^{2} \leq c ({‖J_{1}‖}_{L_{ω_{- μ, - μ}}^{2}}^{2} + {‖J_{2}‖}_{L_{ω_{- μ, - μ}}^{2}}^{2} + {‖J_{3}‖}_{L_{ω_{- μ, - μ}}^{2}}^{2} + {‖J_{4}‖}_{L_{ω_{- μ, - μ}}^{2}}^{2}

+ {‖J_{5}‖}_{L_{ω_{- μ, - μ}}^{2}}^{2} + {‖|ε| + |\hat{ε}|‖}_{L^{2}}^{2}) \leq c ({‖J_{1}‖}_{L_{ω_{- μ, - μ}}^{2}}^{2} + {‖J_{2}‖}_{L_{ω_{- μ, - μ}}^{2}}^{2} + {‖J_{3}‖}_{L_{ω_{- μ, - μ}}^{2}}^{2}

+ {‖J_{4}‖}_{L_{ω_{- μ, - μ}}^{2}}^{2} + {‖J_{5}‖}_{L_{ω_{- μ, - μ}}^{2}}^{2} + {‖| ε | + | \hat{ε} |‖}_{L^{\infty}}^{2}) .

We obtain that from Eqs. (22), (23) and Lemma 3.10:

\begin{matrix} {‖J_{5}‖}_{L_{ω_{- μ, - μ}}^{2}} = {‖(I - I_{N}^{- μ, - μ}) \tilde{M} ε‖}_{L_{ω_{- μ, - μ}}^{2}} = {‖(I - I_{N}^{- μ, - μ}) (\tilde{M} ε - τ_{N} \tilde{M} ε)‖}_{L_{ω_{- μ, - μ}}^{2}} \end{matrix}

\leq c {‖\tilde{M} ε - τ_{N} \tilde{M} ε‖}_{L^{\infty}} \leq c N^{- k} {‖ε‖}_{L^{\infty}} \leq c N^{- k} {‖| ε | + | \hat{ε} |‖}_{L^{\infty}},

{‖J_{2}‖}_{L_{ω_{- μ, - μ}}^{2}} \leq c N^{- k} {‖|ε| + |\hat{ε}|‖}_{L^{\infty}}, {‖J_{3}‖}_{L_{ω_{- μ, - μ}}^{2}} \leq c N^{- k} {‖|ε| + |\hat{ε}|‖}_{L^{\infty}} .

These result, together with the estimates Eqs. (33), (44) and (19), yields (34).

Now subtracting Eq. (28) from Eq. (31) leads to:

\{\begin{array}{l} (\begin{matrix} {\hat{u}}_{N} - u_{N} - I_{N}^{- μ, - μ} Q (t) + I_{N}^{- μ, - μ} M u_{N} - I_{N}^{- μ, - μ} M {\hat{u}}_{N} \\ - I_{N}^{- μ, - μ} \hat{Q} (t) + I_{N}^{- μ, - μ} \hat{M} w_{N} - I_{N}^{- μ, - μ} \hat{M} {\hat{w}}_{N} = 0 \end{matrix}), \\ {\hat{w}}_{N} - w_{N} - I_{N}^{- μ, - μ} \tilde{Q} (t) - I_{N}^{- μ, - μ} \tilde{M} {\hat{u}}_{N} + I_{N}^{- μ, - μ} \tilde{M} u_{N} = 0, \end{array}

which can be simplified as, by setting $E = {\hat{u}}_{N} - u_{N}$ , $E_{1} = {\hat{w}}_{N} - w_{N}$ :

45

\{\begin{array}{l} E - I_{N}^{- μ, - μ} Q (t) - I_{N}^{- μ, - μ} \hat{Q} (t) - I_{N}^{- μ, - μ} M E - I_{N}^{- μ, - μ} \hat{M} E_{1} = 0, \\ E_{1} - I_{N}^{- μ, - μ} \tilde{Q} (t) - I_{N}^{- μ, - μ} \tilde{M} E = 0 . \end{array}

Let $e_{N} = u - u_{N}$ and ${\hat{e}}_{N} = w - w_{N}$ be the error corresponding to the Jacobi pseudo-spectral Galerkin solution $u_{N}$ , $w_{N}$ of Eq. (14). Now we are prepared to get our global convergence result for problem Eq. (3).

Theorem 4.1. Suppose that:

m a x \{{(\frac{T}{2})}^{1 - μ} | K (t, s |, \frac{T}{2} | a (t) |, \frac{T}{2}\} \leq L,

and the solution of Eq. (3) is sufficiently smooth. For the Jacobi pseudo spectral Galerkin solution defined in Eq. (14), we have the following estimates:

1) $L^{\infty}$ norm of $| e_{N} | + | \hat{e_{N}} |$ satisfies:

46

{||| e_{N} | + | \hat{e_{N}} |||}_{L^{\infty}} \leq \{\begin{array}{l} (\begin{matrix} c l o g N N^{\frac{3}{4} - m} ({||u||}_{m, \infty} + {||w||}_{m, \infty}) \\ + c l o g N N^{- m} ({‖|u| + |w|‖}_{L^{\infty}}), - 1 < - μ \leq - \frac{1}{2} \end{matrix}), \\ (\begin{matrix} c N^{\frac{5}{4} - m - μ} ({||u||}_{m, \infty} + {||w||}_{m, \infty}) \\ + c N^{^{\frac{1}{2} - m - μ}} ({‖|u| + |w|‖}_{L^{\infty}}), - \frac{1}{2} < - μ \leq 0 \end{matrix}) . \end{array}

2) $L_{ω - μ, - μ}^{2}$ norm of $| e_{N} | + | \hat{e_{N}} |$ satisfies:

47

{|||e_{N}| + |\hat{e_{N}}|||}_{L_{ω - μ, - μ}^{2}}

\leq \{\begin{matrix} (\begin{matrix} c l o g N N^{- m} {||| u | + | w |||}_{L^{\infty}} + c l o g N N^{\frac{3}{4} - m} ({||u||}_{m, \infty} + {||w||}_{m, \infty}) \\ + c N^{- m} ({||\partial_{t}^{m} u||}_{ω_{m - μ, m - μ}} + {||\partial_{t}^{m} w||}_{ω_{m - μ, m - μ}}), - 1 < - μ \leq - \frac{1}{2} \end{matrix}), \\ (\begin{matrix} c N^{^{\frac{1}{2} - m - μ}} {|||u|| + ||w|||}_{L^{\infty}} + c N^{\frac{5}{4} - m - μ} ({||u||}_{m, \infty} + {||w||}_{m, \infty}) \\ + c N^{- m} ({||\partial_{t}^{m} u||}_{ω_{m - μ, m - μ}} + {||\partial_{t}^{m} w||}_{ω_{m - μ, m - μ}}), - \frac{1}{2} < - μ \leq 0 \end{matrix}) . \end{matrix}

Proof. We first prove the existence and uniqueness of the Jacobi pseudo-spectral Galerkin solution $u_{N}$ , $w_{N}$ . As the dimension of $P_{N} (Λ)$ is finite and Eqs. (14) and (28) are equivalent, we only need to prove that the solution of Eq. (28) is $u_{N} = w_{N} = 0$ when $g = y_{0} = 0 .$

For this purpose, we consider the equation:

48

\{\begin{array}{l} u_{N} + I_{N}^{- μ, - μ} Q (t) - I_{N}^{- μ, - μ} M u_{N} + I_{N}^{- μ, - μ} \hat{Q} (t) - I_{N}^{- μ, - μ} \hat{M} w_{N} = 0, \\ w_{N} + I_{N}^{- μ, - μ} \tilde{Q} (t) - I_{N}^{- μ, - μ} \tilde{M} u_{N} = 0 . \end{array}

Obviously Eq. (48) can be written as:

\begin{matrix} u_{N} - M u_{N} - \hat{M} w_{N} = I_{N}^{- μ, - μ} M u_{N} - M u_{N} + I_{N}^{- μ, - μ} \hat{M} w_{N} - \hat{M} w_{N} \end{matrix}

- I_{N}^{- μ, - μ} Q (t) - I_{N}^{- μ, - μ} \hat{Q} (t) = R_{1} + R_{2} + R_{3} + R_{4},

and:

w_{N} - \tilde{M} u_{N} = I_{N}^{- μ, - μ} \tilde{M} u_{N} - \tilde{M} u_{N} - I_{N}^{- μ, - μ} \tilde{Q} (t) = R_{5} + R_{6},

namely:

49

\{\begin{array}{l} u_{N} = \frac{T}{2} \int_{- 1}^{t} (a (s) u_{N} (s) + w_{N} (s)) d s + R_{1} + R_{2} + R_{3} + R_{4}, \\ w_{N} = {(\frac{T}{2})}^{1 - μ} \int_{- 1}^{t} (t - s)^{- μ} k (t, s) u_{N} (s) d s + R_{5} + R_{6} . \end{array}

With:

R_{1} = I_{N}^{- μ, - μ} M u_{N} - M u_{N}, R_{2} = I_{N}^{- μ, - μ} \hat{M} w_{N} - \hat{M} w_{N}, R_{3} = - I_{N}^{- μ, - μ} Q (t),

R_{4} = - I_{N}^{- μ, - μ} \hat{Q} (t), R_{5} = I_{N}^{- μ, - μ} \tilde{M} u_{N} - \tilde{M} u_{N}, R_{6} = - I_{N}^{- μ, - μ} \tilde{Q} (t) .

Using Eq. (49) gives:

\{\begin{array}{l} |u_{N}| \leq | R_{1} | + | R_{2} | + | R_{3} | + | R_{4} | + L \int_{- 1}^{t} (|u_{N} (s)| + |w_{N} (s)|) d s, \\ |w_{N}| \leq | R_{5} | + | R_{6} | + L \int_{- 1}^{t} (t - s)^{- μ} (|u_{N} (s)| + |w_{N} (s)|) d s . \end{array}

Namely:

50

\begin{matrix} (|u_{N}| + |w_{N}|) \leq | R_{1} | + | R_{2} | + | R_{3} | + | R_{4} | + | R_{5} | + | R_{6} | \end{matrix}

+ c L \int_{- 1}^{t} ((t - s)^{- μ} + 1) (|u_{N} (s)| + |w_{N} (s)|) d s .

Using Lemma 3.7 yields:

51

{||(|u_{N}| + |w_{N}|)||}_{L^{\infty}}

\leq c ({||R_{1}||}_{L^{\infty}} + {||R_{2}||}_{L^{\infty}} + {||R_{3}||}_{L^{\infty}} + {||R_{4}||}_{L^{\infty}} + {||R_{5}||}_{L^{\infty}} + {||R_{6}||}_{L^{\infty}}) .

On the other hand, according to Lemma 3.9:

52

{||R_{6}||}_{L^{\infty}}^{2} = {||- I_{N}^{- μ, - μ} \tilde{Q} (t)||}_{L^{\infty}}^{2} \leq \{\begin{array}{l} c (l o g N)^{2} {||\tilde{Q} (t)||}_{L^{\infty}}^{2}, - 1 < - μ \leq - \frac{1}{2}, \\ c N^{1 - 2 μ} {||\tilde{Q} (t)||}_{L^{\infty}}^{2}, - \frac{1}{2} < - μ < 0 . \end{array}

By the expression of $\tilde{Q} (t)$ in Eq. (25), Lemma 3.2, we have:

|\tilde{Q} (t)| \leq c N^{- m} \sqrt{(\frac{t + 1}{2})} {||\partial_{θ}^{m} (k (τ (t, θ)) ω_{0, μ} (θ))||}_{L_{ω_{m - μ, m - μ}}^{2}} {||u_{N}||}_{L_{ω_{- μ, - μ}}^{2}}

\leq c N^{- m} {||u_{N}||}_{L_{ω_{- μ, - μ}}^{2}},

which, together with Eq. (52), gives:

53

{||R_{6}||}_{L^{\infty}} \leq \{\begin{array}{l} c l o g N N^{- m} {||(|u_{N}| + |w_{N}|)||}_{L^{\infty}}, - 1 < - μ \leq - \frac{1}{2}, \\ c N^{^{\frac{1}{2} - m - μ}} {||u_{N}||}_{L^{\infty}} \leq c N^{^{\frac{1}{2} - m - μ}} {||(|u_{N}| + |w_{N}|)||}_{L^{\infty}}, - \frac{1}{2} < - μ < 0 . \end{array}

Similarly, Eq. (53) holds for ${||R_{3}||}_{L^{\infty}}$ and ${||R_{4}||}_{L^{\infty}}$ .

The combination of Eqs. (43) and (53) yields:

54

{||(|u_{N}| + |w_{N}|)||}_{L^{\infty}} \leq \{\begin{array}{l} c (l o g N N^{- m} + l o g N N^{- κ}) {||(|u_{N}| + |w_{N}|)||}_{L^{\infty}}, - 1 < - μ \leq - \frac{1}{2}, \\ c (N^{^{\frac{1}{2} - m - μ}} + N^{^{\frac{1}{2} - κ - μ}}) {||(|u_{N}| + |w_{N}|)||}_{L^{\infty}}, - \frac{1}{2} < - μ < 0 . \end{array}

Based on Eq. (54) and Lemma 3.4 with $κ + μ > 1 / 2,$ when $N$ is large enough, $u_{N} = w_{N} = 0$ . As a result, the existence and uniqueness of the Jacobi pseudo-spectral Galerkin solutions $u_{N}$ , $w_{N}$ are proved.

Now we turn to the $L^{\infty}$ error estimate. Actually Eq. (45) can be transformed into:

55

\{\begin{array}{l} (\begin{array}{l} E = \frac{T}{2} \int_{- 1}^{t} (a (s) E_{N} (s) + E_{1} (s)) d s - M E + I_{N}^{- μ, - μ} M E \\ - \hat{M} E_{1} + I_{N}^{- μ, - μ} \hat{M} E_{1} + I_{N}^{- μ, - μ} Q (t) + I_{N}^{- μ, - μ} \hat{Q} (t) \end{array}), \\ E = {(\frac{T}{2})}^{1 - μ} \int_{- 1}^{t} (t - s)^{- μ} k (t, s) E (s) d s - \tilde{M} E + I_{N}^{- μ, - μ} \tilde{M} E + I_{N}^{- μ, - μ} \tilde{Q} (t), \end{array}

which yields:

56

|E| + |E_{1}|

\leq c \int_{- 1}^{t} ((t - s)^{- μ} + 1) (|E| + |E_{1}|) d s + |R_{7}| + |R_{8}| + |R_{9}| + |R_{3}| + |R_{4}| + |R_{6}|,

with $R_{7} = I_{N}^{- μ, - μ} Μ E - Μ E$ , $R_{8} = I_{N}^{- μ, - μ} \hat{Μ} E_{1} - \hat{Μ} E_{1}$ , $R_{9} = I_{N}^{- μ, - μ} \tilde{Μ} E - \tilde{Μ} E$ .

Similar to Eq. (52), it follows from Eq. (56) and Lemma 3.7 that:

57

{‖|E| + |E_{1}|‖}_{L^{\infty}} \leq c ({‖R_{7}‖}_{L^{\infty}} + {‖R_{8}‖}_{L^{\infty}} + {‖R_{9}‖}_{L^{\infty}} + {‖R_{3}‖}_{L^{\infty}} + {‖R_{4}‖}_{L^{\infty}} + {‖R_{6}‖}_{L^{\infty}}) .

Similar to the estimate of Eq. (43), we obtain:

58

{‖R_{9}‖}_{L^{\infty}} \leq \{\begin{array}{l} c l o g N N^{- k} {‖E‖}_{L^{\infty}}, - 1 < - μ < - \frac{1}{2}, \\ c N^{\frac{1}{2} - k - μ} {‖E‖}_{L^{\infty}}, - \frac{1}{2} < - μ < 0 . \end{array} .

It also holds for $R_{7}$ and $R_{8}$ . In terms of Eqs. (53), (57) and (58), when $N$ is large enough, we obtain:

59

{‖|E| + |E_{1}|‖}_{L^{\infty}} \leq \{\begin{array}{l} (\begin{matrix} c l o g N N^{- m} {‖(|u_{N}| + |w_{N}|)‖}_{L^{\infty}} \leq c l o g N N^{- m} ({‖(|u| + |w|)‖}_{L^{\infty}} \\ + {‖(|u - u_{N}| + |w - w_{N}|)‖}_{L^{\infty}}), - 1 < - μ \leq - \frac{1}{2} \end{matrix}), \\ (\begin{matrix} c N^{\frac{1}{2} - m - μ} {‖(|u_{N}| + |w_{N}|)‖}_{L^{\infty}} \leq c N^{\frac{1}{2} - m - μ} ({‖(|u| + |w|)‖}_{L^{\infty}} \\ + {‖(|u - u_{N}| + |w - w_{N}|)‖}_{L^{\infty}}), - \frac{1}{2} < - μ < 0 \end{matrix}) . \end{array}

By the triangular inequality:

60

{‖|u - u_{N}| + |w - w_{N}|‖}_{L^{\infty}} \leq {‖|u - {\hat{u}}_{N}| + |w - {\hat{w}}_{N}|‖}_{L^{\infty}}

+ {‖|{\hat{u}}_{N} - u_{N}| + |{\hat{w}}_{N} - w_{N}|‖}_{L^{\infty}} = {‖|u - {\hat{u}}_{N}| + |w - {\hat{w}}_{N}|‖}_{L^{\infty}} + {‖|E| + |E_{1}|‖}_{L^{\infty}},

as well as Eqs. (59), (60) and Lemma 4.1, we can obtain the estimated Eq. (46) provided $N$ is sufficiently large.

Next we prove Eq. (47). Using Lemma 3.7 and the generalized Hardy inequality (Lemma 3.8, $p = q =$ 2), one obtains that from Eq. (56):

61

{‖|E| + |E_{1}|‖}_{L_{ω_{- μ, - μ}}^{2}}^{2} \leq c ({‖R_{7}‖}_{L_{ω_{- μ, - μ}}^{2}}^{2} + {‖R_{8}‖}_{L_{ω_{- μ, - μ}}^{2}}^{2} + {‖R_{9}‖}_{L_{ω_{- μ, - μ}}^{2}}^{2}

+ {‖R_{3}‖}_{L_{ω_{- μ, - μ}}^{2}}^{2} + {‖R_{4}‖}_{L_{ω_{- μ, - μ}}^{2}}^{2} + {‖R_{6}‖}_{L_{ω_{- μ, - μ}}^{2}}^{2} + {‖|E| + |E_{1}|‖}_{L^{\infty}}^{2}) \leq c ({‖R_{7}‖}_{L^{\infty}}^{2}

+ {‖R_{8}‖}_{L^{\infty}}^{2} + {‖R_{9}‖}_{L^{\infty}}^{2} + {‖R_{3}‖}_{L^{\infty}}^{2} + {‖R_{4}‖}_{L^{\infty}}^{2} + {‖R_{6}‖}_{L^{\infty}}^{2} + {‖|E| + |E_{1}|‖}_{L^{\infty}}^{2}) .

The combination of Eqs. (53), (58) and (59) yields:

62

{‖|E| + |E_{1}|‖}_{_{ω_{- μ, - μ}}^{2}}

\leq \{\begin{array}{l} c l o g N N^{- m} ({‖(|u| + |w|)‖}_{L^{\infty}} + ‖(|e_{N}| + |{\hat{e}}_{N}|)‖ {}_{L^{\infty}}), - 1 < - μ \leq - \frac{1}{2}, \\ c N^{\frac{1}{2} - m - μ} ({‖(|u| + |w|)‖}_{L^{\infty}} + {‖|e_{N}| + |{\hat{e}}_{N}|‖}_{L^{\infty}}), - \frac{1}{2} < - μ < 0 . \end{array}

By the triangular inequality again:

63

{‖|e_{N}| + |{\hat{e}}_{N}|‖}_{L_{ω_{- μ, - μ}}^{2}} \leq {‖(|u - {\hat{u}}_{N}| + |w - {\hat{w}}_{N}|)‖}_{L_{ω_{- μ, - μ}}^{2}} + {‖|E| + |E_{1}|‖}_{L_{ω_{- μ, - μ}}^{2}} .

In terms of Eqs. (46), (62), (63) and Lemma 4.1, we obtain the desired result.

5. Numerical results

We give two numerical examples to confirm our analysis.

Example 1. Consider the Volterra integro-differential equation:

u^{¢} (t) = 2 t u (t) + (1 - 2 t) e^{t} - \frac{4}{3} (1 + t)^{\frac{3}{4}} + \int_{- 1}^{t} (t - τ) -^{\frac{1}{4}} e^{- τ} u (τ) d τ .

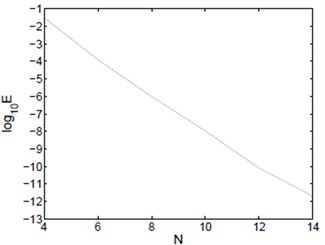
The exact solution is $u (t) = e^{t}$ . Fig. 1 shows the errors $u - u_{N}$ of approximate solution in $L^{\infty}$ and Fig. 2 shows the errors weighted $L_{ω_{- μ, - μ}}^{2}$ norms obtained by using the Pseudo-spectral methods described above. It is observed that the desired exponential rate of convergence is obtained.

Example 2. Consider the Volterra equation integro-differential equation:

u^{¢} (t) = e^{t} u (t) - \frac{16}{5} (1 + t)^{\frac{5}{4}} + 4 (1 + t)^{\frac{1}{4}}

- (s i n (t) + e^{t} c o s (t)) + \int_{- 1}^{t} (t - τ)^{- \frac{3}{4}} \frac{τ}{c o s (τ)} u (τ) d τ .

The corresponding exact solution is given by $u (t) = c o s (t)$ . Fig. 3 and Fig. 4 plot the errors $u - u_{N}$ for 2 $\leq N \leq$ 14 in $L^{\infty}$ and $L_{ω_{- μ, - μ}}^{2}$ norms. Once again the desired spectral accuracy is obtained.

Fig. 1L∞ error of Example 1

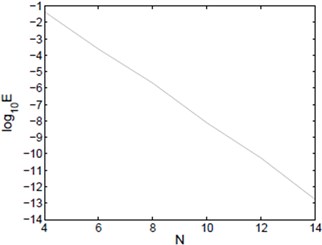
Fig. 2Lω-μ,-μ2 error of Example 1

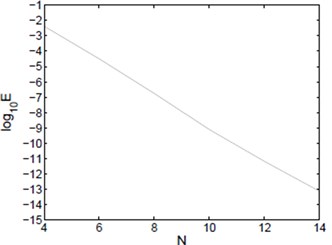
Fig. 3L∞ error of Example 2

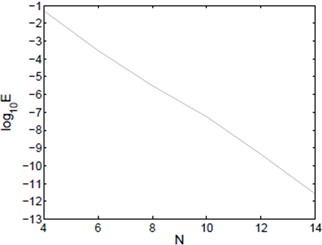
Fig. 4Lω-μ,-μ2 error of Example 2

6. Concluding remarks

This work is concerned with the Jacobi pseudospectral-Galerkin methods for solving Volterratype integro-differential equation and the error analysis. To facilitate the use of the methods, we first restate the original integro-differential equation as two simple integral equations of the second kind, then the spectral accuracy associated with $L^{\infty}$ and $L_{ω_{- μ, - μ}}^{2}$ error estimates are demonstrated theoretically. These results are confirmed by some numerical experiments.

We only investigated the case when the solution is smooth in the present work, with the availability of this methodology, it will be possible to extend the results of this paper to the weakly singular VIDEs with nonsmooth solutions which will be the subject of our future work.

References

Brunner H. Collocation Methods for Volterra Integral and Related Functional Equations. Cambridge University Press, Cambridge, 2004.

Search CrossRef
Chen Y., Tang T. Spectral methods for weakly singular Volterra integral equations with smooth solutions. Journal of Computational and Applied Mathematics, Vol. 233, 2009, p. 938-950.

Search CrossRef
Tao Xia, Xie Ziqing, Zhou Xiaojun Spectral Petrov-Galerkin methods for the second kind Volterra type integro-differential equations. Numerical Mathematics: Theory, Methods and Applications, Vol. 4, Issue 2, 2011, p. 216-236.

Search CrossRef
Ali I., Brunner H., Tang T. A spectral method for pantograph-type delay differential equations and its convergence analysis. Journal of Computational Mathematics, Vol. 27, Issues 2-3, 2009, p. 254-265.

Search CrossRef
Brunner H., Schotzau D. Hp-discontinuous Galerkin time-stepping for Volterra integro-differential equations. SIAM Journal on Numerical Analysis, Vol. 44, 2006, p. 224-245.

Search CrossRef
Shen J., Tang T., Wang L.-L. Spectral Methods: Algorithms, Analysis and Applications. Springer Series in Computational Mathematics. Springer, New York, 2011.

Search CrossRef
Wang W. Mechanical algorithm for solving the second kind of Volterra integral equation. Applied Mathematics and Computation, Vol. 173, 2006, p. 1149-1162.

Search CrossRef
Bock I., Lovisek J. On a reliable solution of a Volterra integral equation in a Hilbert space. Applications of Mathematics, Vol. 48, Issue 6, 2003, p. 469-486.

Search CrossRef
Brunner H. The numerical solutions of weakly singular Volterra integral equations by collocation on graded meshes. Mathematics of Computation, Vol. 45, 1985, p. 417-437.

Search CrossRef
Brunner H. Polynomial spline collocation methods for Volterra integro-differential equations with weakly singular kernels. IMA Journal on Numerical Analysis, Vol. 6, 1986, p. 221-239.

Search CrossRef
Canuto C., Hussaini M. Y., Quarteroni A., Zang T. A. Spectral Methods Fundamentals in Single Domains. Springer-Verlag, Berlin, 2006.

Search CrossRef
Ragozin D. L. Polynomial approximation on compact manifolds and homogeneous spaces. Transactions of the American Mathematical Society, Vol. 150, 1970, p. 41-53.

Search CrossRef
Ragozin D. L. Constructive polynomial approximation on spheres and projective spaces. Transactions of the American Mathematical Society, Vol. 162, 1971, p. 157-170.

Search CrossRef
Chen Y., Tang T. Convergence analysis of the Jacobi spectral-collocation methods for Volterra integral equations with a weakly singular kernel. Mathemacics of Computation, Vol. 79, 2010, p. 147-167.

Search CrossRef
Willett D. A linear generalization of Gronwall’s inequality. Proceedings of the American Mathematical Society, Vol. 16, Issue 4, 1965, p. 774-778.

Search CrossRef
Gogatishvili A., Lang J. The generalized Hardy operator with kernel and variable integral limits in Banach function spaces. Journal of Inequalities and Applications, Vol. 4, Issue 1, 1999, p. 1-16.

Search CrossRef
Kufner A., Persson L. E. Weighted Inequalities of Hardy Type. World Scientific, River Edge, NJ, 2003.

Search CrossRef
Atkinson K. E. A Survey of Numerical Methods for the Solution of Fredholm Integral Equations of the Second Kind. SIAM, Philadelphia, 1976.

Search CrossRef
Lubich Ch. Fractional linear multi-step methods for Abel-Volterra integral equations of the second kind. Mathematics of Computation, Vol. 45, 1985, p. 463-469.

Search CrossRef
Federson M., Bianconi R., Barbanti L. Linear Volterra integral equations as the limit of discrete systems. Cadernos de Matematica, Vol. 4, 2003, p. 331-352.

Search CrossRef
Shen J., Tang T. Spectral and High-Order Methods with Applications. Science Press, Beijing, 2006.

Search CrossRef
Tang T. A note on collocation methods for Volterra integro-differential equations with weakly singular kernels. IMA Journal of Numerical Analysis, Vol. 13, 1993, p. 93-99.

Search CrossRef
Tang T., Xu X., Chen J. On spectral methods for Volterra type integral equations and the convergence analysis. Journal of Computational Mathematics, Vol. 26, 2008, p. 825-837.

Search CrossRef
Jiang Y. J. On spectral methods for Volterra-type integro-differential equations. Journal of Computational and Applied Mathematics, Vol. 230, 2009, p. 333-340.

Search CrossRef
Wan Zhengsu, Chen Yanping, Huang Yunqing Legendre spectral Galerkin method for second-kind Volterra integral equations. Frontiers of Mathematics in China, Vol. 4, Issue 1, 2009, p. 181-193.

Search CrossRef

About this article

Received

07 November 2013

Accepted

20 November 2014

Published

30 December 2014

Keywords

Volterra integro-differential equation

Jacobi pseudo-spectral method

weakly singular kernel

convergence

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China (51279099), Shanghai Natural Science Foundation (12ZR1412500), Innovation Program of Shanghai Municipal Education Commission (13ZZ124).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.